核心素养下数学内容本质的揭示与思想方法的渗透——一个线面角模型及其运用

浙江省衢州第二中学 (324000) 万 祺

直线与平面所成的角是线面位置关系的重要组成部分.线面角和二面角一起构成了空间角的概念体系，这些概念对于提高学生的空间位置关系的认知能力，发展学生的空间想象思维起着重要的作用.线面角在近几年高考、学考题中更是成为了高频考点.这类试题一般处于小题压轴题和解答题位置，具有很高的区分度，能积极发挥考试的选拔功能.本文通过挖掘线面角定义，探寻线面角模型的本质，解决一类与线面角相关的高考试题.

图1

1.模型呈现

(2016年浙江省学业水平考试试题)如图1所示，在侧棱垂直于底面的三棱柱ABC-A1B1C1中，P是棱BC上的动点，记直线A1P与平面ABC所成的角为θ1，与直线BC所成的角为θ2，则θ1，θ2的大小关系是( ).

A.θ1=θ2B.θ1>θ2C.θ1<θ2D.不能确定

2.问题解决

2.1 大胆猜想

本题涵盖了线面角的定义，异面直线所成的角等概念，要求学生深刻理解线面角的定义与本质.当然，作为选择题，本题也可采用特殊化的思想，如存在某个时刻使得直线A1P与直线BC所成的角是直角，而此时线面角θ1仍为锐角，因此选C.

2.2 严谨论证

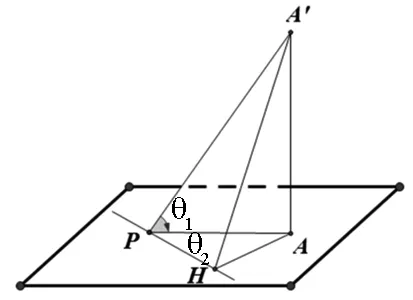
图2

∵cosθ2<1，∴cosθθ1①.∵cosθ1<1，∴cosθθ2②.

我们发现如下结论：

①线面角θ1是斜线A′P与平面内所有直线所成角中的最小角；

②平面的一条斜线与平面内一条直线l所成的角大于斜线在平面内的射影与l所成的角.

至此，再回头看上面的学考题，结果是显然的.

3.模型应用

图3

例1 (2015年浙江省学业水平考试)如图3，在菱形ABCD中，∠BAD=60°，线段AD,BD的中点分别为E,F. 现将ΔABD沿对角线BD翻折，则异面直线BE与CF所成角的取值范围是( ).

图4

图5

图6

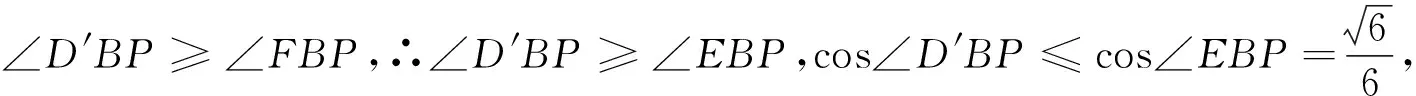
例3 (2017全国卷)a,b为空间中两条互相垂直的直线，等腰RtΔABC的直角边AC所在直线与a,b都垂直，斜边AB以AC为旋转轴旋转，有下列结论：

①当直线AB与a成60°角时，AB与b成30°角；

②当直线AB与a成60°角时，AB与b成60°角；

③直线AB与a所成角的最小值是45°；

④直线AB与a所成角的最大值是60°；其中正确的是.

图7

解:如图7,AC,a,b两两垂直，斜边AB以AC为旋转轴旋转，作BD∥a，BE∥b，当直线AB与a成60°角时，因为∠ABC=45°，由三余弦定理，cos∠ABD=cos∠ABC·cos∠DBC得cos60°=cos45°·cos∠DBC，∠DBC=45°，所以∠EBC=45°.

由三余弦定理，cos∠ABE=cos∠ABC·cos∠EBC得∠ABE=60°,所以AB与b成60°角；再由最小角定理知∠ABD≥∠ABC=45°,故直线AB与a所成角的最小值是45°，又因为直线AB与a可以成直角，所以②③正确.

图8

解:一方面，①AB与EF是一对异面直线；②异面直线在同一平面上的射影可以是一对平行线;③当EF以直线AB为轴旋转，且AB∥平面α.

由①②③可知旋转过程中必存在某一时刻，使得直线AB与EF在α内射影相互平行，此时所求余弦值为1.

图9

另一方面，由AB∥平面α，不妨AB⊂α，作AP∥EF，PH⊥α，垂足是H，如图9,故∠HAB≤∠PAB，所以

图10

例5 如图10,已知在正四面体ABCD中，E为BC中点，F为直线BD的一点，则平面AEF与平面ACD所成角的正弦值的取值范围是.

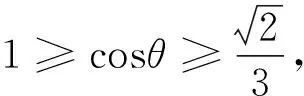
例6 (2018浙江卷)已知四棱锥S-ABCD的底面是正方形，侧棱长均相等，E是线段AB上的点(不含端点)，设SE与BC所成的角是θ1，SE与平面ABCD所成的角是θ2，二面角S-AB-C的平面角为θ3，则( ).

A.θ1≤θ2≤θ3B.θ3≤θ2≤θ1

C.θ1≤θ3≤θ2D.θ2≤θ3≤θ1

图11

解:如图11,设S在底面的射影是点O，过点E作EF∥BC交CD于点F，则θ1=∠SEF，θ2=∠SEO，作OH⊥AB，垂足是H，则θ3=∠SHO，由OH≤OE可知tanθ3≥tanθ2，即θ3≥θ2，故B、C错误，再由线面角的最小性可知∠SEO≤∠SEF,故θ2≤θ1，从而A错误，因此选D.

事实上也可直接比较θ3,θ1的大小，考虑直线OH与平面SAB所成的线面角即为θ3，而直线OH与平面SAB内的直线SE所成的角即为θ1，由线面角的最小性可知θ3≤θ1.

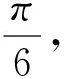
波利亚在《怎样解题》中将“回顾反思”作为解题的四大步中的最后一步，我想，在平日的教学研究工作当中也应如此.只有真正理解数学定义，善于抓住问题的本质，才能在数学的世界里走得更远.