让核心素养在数学课堂悄然生长——“幂函数”教学设计与思考

广东省惠州市东江高级中学 (516000) 李 旭 冯祖琨

《普通高中数学课程标准(2017年)》指出了数学学科核心素养，并将数学学科核心素养作为数学课程的重要目标，在课程目标、课程内容、学业质量等方面都对数学学科核心素养提出了具体要求.这些要求最终要落实到教学中去，这就要求教师在确定教学目标，进行教学设计时，关注数学学科核心素养.而在具体教学中，利用信息技术可以创设丰富的教学情境，可以帮助学生自主探究和解决问题，可以将一些抽象的数学内容通过直观演示变得直观可视等.下面以幂函数为例，谈谈如何借助TI图形计算器进行教学设计，让核心素养在数学课堂中悄然生长.

1.教学目标

1.1 理解幂函数的概念，会研究常见幂函数的性质，并能根据函数性质作出其大致图像；

1.2 在幂函数的性质与图像的探究过程中，感悟数形结合、从特殊到一般、化归等数学思想.在生生互动和师生互动中，进一步增强发现和提出问题、分析和解决问题的能力；

1.3 在幂函数的教学过程中，使得逻辑推理、直观想象、数学运算、数学抽象等数学核心素养在更髙水平上得到提升.

2.教学重难点

教学重点：幂函数y=xα(α为常数)作图以及性质的探究.

教学难点：归纳幂函数的性质.

设计意图：本节课是第二章第2.3节第1课时的内容.幂函数作为重要的函数模型，是学生在高中阶段系统学习了函数的性质后，第一次全面研究的某一类函数.本节课在学生已经掌握函数的一般性质和几个简单函数的基础上，引出幂函数的概念，研究几个典型幂函数的图像与性质.一方面可以进一步深化学生对函数概念的理解与认识，另一方面也为今后进一步熟悉函数的性质和作用、研究指函数和对数函数的性质打下坚实的基础.同时，结合新高考的要求，以及数学改革的方向，要在教学的过程中，体现并融入核心素养.因此，本文在教学设计时，借助TI图形计算器，进行合理的教学设计，让数学核心素养在课堂中悄然生长.

3.教学过程

3.1 情境创设

问题1请写出下列函数的解析式：

①如果某人购买了每千克1元的蔬菜w千克，那么他需要付的钱数P(元)关于购买的蔬菜量w(千克)的函数解析式为.

②如果正方形的边长为a，那么正方形的面积S关于a的函数解析式为.

③如果正方体的边长为a，那么正方体的体积V关于a的函数解析式为.

④如果正方形的面积为S，那么正方形的边长a关于S的函数解析式.

⑤如果某人ts内骑车行进了1km，那么他骑车的速度v(km/s)关于t的函数解析式为.

设计意图：从旧知到新知，这样的引入显得十分自然，学生感受到幂函数来自于生活顺利地建立了新、旧知识之间的联系，增强数学的应用性和趣味性.

问题2如果将上述函数解析式左侧的因变量改成y，右侧的自变量改成x，请仔细观察得到的函数解析式，它们具有什么共同特征？是指数函数吗？

设计意图：从特殊到一般，将实际问题转化为数学问题，同时，统一自变量与因变量之后，让学生更能直观地感知幂函数解析式的共同特征，达到锻炼学生的观察能力与概括能力的目的.体现数学的核心素养逻辑推理和数学建模.

3.2 概念引入

师：经过以上的分析，我们把形如y=xα(α为常数)的函数叫作幂函数，其中x是自变量，α是常数.

问题3你能说出幂函数y=xα(α为常数)与指数函数y=ax(a>0且a≠1)有什么区别吗？

生3：这两个函数的自变量的位置与常数的位置是颠倒过来的.

设计意图：针对学生容易将幂函数和指数函数混淆的情况，组织学生对两类函数的解析式进行对比，从而达到强化记忆的目的.

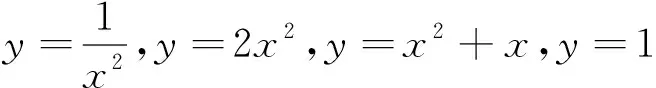
3.3 新知探究

问题4研究函数一般从哪些方面着手？类比之前研究指数函数、对数函数的方法你准备怎样研究幂函数？

生4：研究函数一般从其定义域、值域、奇偶性与单调性等方面着手，考虑借助幂函数的图像研究幂函数的性质.

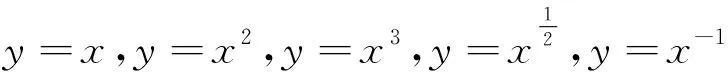
生：用TI图形计算器作图

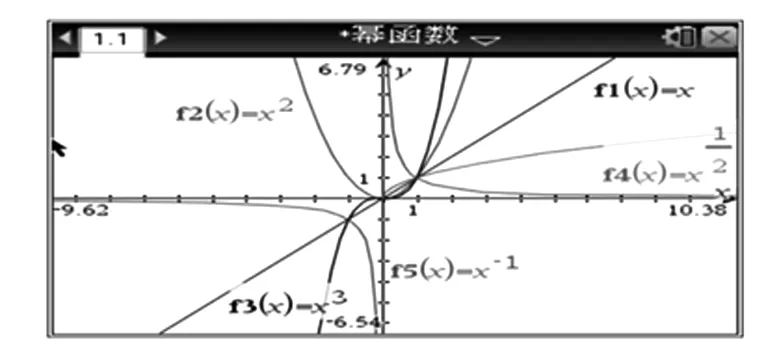
图1

问题5根据上述图像的特征，填写下面的表格(生5回答，教师板书)：

y=xy=x2y=x3y=x12y=x-1定义域RRR[0,+∞){x|x≠0}值域R[0,+∞)R[0,+∞){y|y≠0}奇偶性奇函数偶函数奇函数非奇非偶奇函数单调性R上增(-∞,0)减(0,+∞)增R上增(0,+∞)增(-∞,0)减(0,+∞)减

师：从上表可以看出，幂函数随着幂指数的取值不同，它们的图像和性质存在着较大的差异，下面就请同学们通过观察上述函数的图像来探寻幂函数的一些共性，我们来看以下5个问题：定义域、值域、单调性、奇偶性、公共点.

问题6幂函数图像过定点及象限的情况？

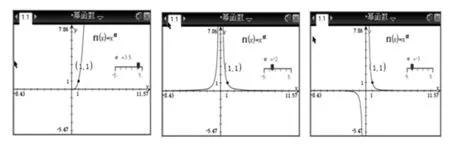
图2

生6：通过TI图形计算器，改变α的取值(如图2)发现幂函数y=xα(α为常数)过定点(1，1)，不一定过点(0，0)；幂函数图像过第一象限，不过第四象限.

师：能利用幂函数的解析式解释其中的原因吗？

生7：因1α=1，因此幂函数过定点(1，1)；当x>0时，xα>0，因此幂函数图像过第一象限.

问题7幂函数在区间(0，+∞)上的单调性如何？

生8：借助图形计算器作出5个具有代表性的幂函数在第一象限内的图像，通过图3观察α>0时，幂函数y=xα在(0，+∞)上是增函数；α<0时，幂函数y=xα在(0，+∞)上是减函数.

师：α=0呢？另，通过幂函数在区间(0，+∞)上的单调性，你能判断幂函数在区间(-∞，0)上的单调性吗？

生9：当α=0时，幂函数变为y=x0=1(x≠0)，此时无单调性.当α≠0时，判断幂函数在区间(-∞，0)上的单调性借助函数的奇偶性判断即可.

师：通过5个具有代表性的幂函数，我们猜想了幂函数的单调性与α之间的关系，能否借助图形计算器进行验证呢？

生10：通过TI图形计算器，分别在α>0与α<0范围内改变α的取值得到一般性规律(如图4).

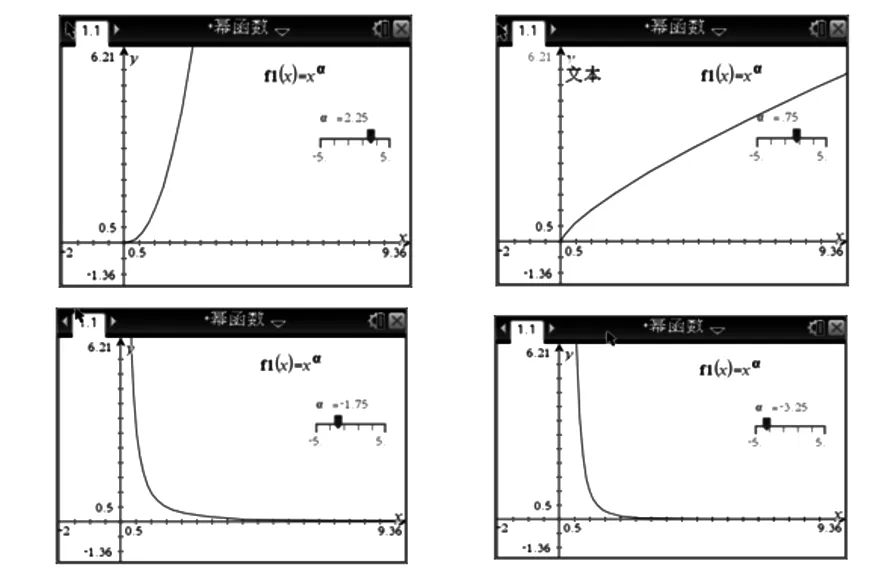
图4

问题8：当α>0时，幂函数y=xα在(0，+∞)上的图像的高低与指数的变化有何关系？

图5

问题9幂函数y=xα(x∈(0,+∞))，α>1与α<1的图像有何不同？

图6

生12：操作TI图形计算器，并由图6可知，当α>1时，幂函数y=xα的图像向下凸出；当0<α<1时，幂函数y=xα的图像向上凸出.

问题10y=xα(α<0)在(0，+∞)递减，图像特征又如何呢？

生13：观察图7可知：当α<0时，幂函数y=xα在第一象限的图像向上与y轴无限接近，向右与x轴无限接近.

图7

设计意图：问题串建构教学更容易让学生参与其中，更容易理解.课堂教学中，“自然的过程”来源于数学知识发生发展过程和学生认知过程的融合，具体表现为对数学概念、原理的不断归纳和概括的过程”，而实现这种“自然的过程”的关键，是提出恰到好处的问题和设计精细的过程.

4.课堂例题

例1 已知y=(m2+2m-2)xm2-1+2n-3是幂函数，求m，n的值．

例2 比较下列各题中两个值的大小：

例3 已知m∈(0,1)，令a=logm2，b=m2，c=2m，那么a,b,c之间的大小关系为( ).

A．b

C．a

思考：数学教学过程是数学活动的过程，也是数学思维活动的过程.学生“动起来”是产生数学思维活动的关键，而学生活动的驱动力就来源于问题.教师采用了问题串的形式展开教学，更有利于知识的理解和记忆，也能增强学生学习数学的参与性和趣味性.同时，借助TI图形计算器，数形结合，更有利于知识的理解；幂函数性质的获得难以一步到位，教学活动借助问题串层层推进，一步步揭开幂函数的神秘面纱.根据学生认知规律的螺旋上升安排教学内容——从观察整个图象找幂函数性质，缩小到第一象限找规律，层层递进，给学生提供反复认识的机会，符合学生的认知规律.知识的产生、方法的由来从学生头脑里自然而然的流淌出来.这样的设计能够使学生产生“其言皆若出于吾口，其意皆若出于吾心”的感觉，最终达到教学内容自然生成的目的.学生的数学核心素养，并非孤立的，而是相互依存、相互促进的.数学建模素养的培养，可以有效带动数据分析、逻辑推理、数学抽象和数学运算等素养的综合提升.核心素养的培养，是一个循序渐进的“慢工程”，任重而道远.关注学生知识理解与迁移程度是一个切实可行的抓手，以此来发展学生的数学核心素养，能够让数学核心素养这一抽象概念在数学课堂落地生根.