基于ARMA模型对财政收入的实证研究分析

文| 王馨怡

财政是政府为满足社会条件的需要而发行的社会产品。随着经济的高水平发展，社会产品的生产量将增加，财政收入也将相应增加。财政收入在实现国家宏观调控和优化资源配置中发挥着重要作用。以适应经济发展需要，保持经济社会稳定协调发展。近年来，中国经济发展水平不断提高，财政收入也保持了快速增长的态势。

财政收入占国内生产总值(GDP)的比重不断提高，财政收入增长与经济增长之间的互动关系成为一个值得关注的问题。本文选取2008年1季度至2019年3季度的财政收入的数据，采用ARMA模型对未来47个季度的财政收入对经济发展影响进行分析。

ARMA模型的构建

输入数据检验序列是否符合白噪声即是否平稳，之后再计算ACF、PACF发现并不在低阶结尾，因此我们选用ARMA模型。

数据的检验与分析

平稳性检验

导入财政收入2008年1季度到2019年3季度的对数收益率数据，得到对数时序图，如下图所示。

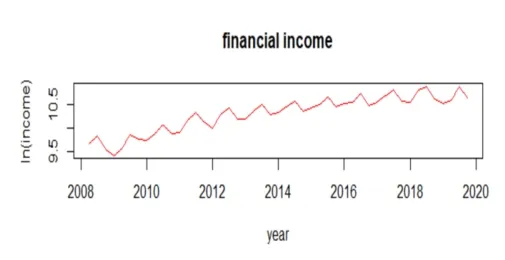
图1

图2

图1显示，从2010年-2019年总体呈上涨趋势并且伴有规律的波动，其中，第1季度和第3季度对数较小，呈下降趋势；第2季度和第4季度整体呈上升趋势，说明该对数具有高度的样本序列相关性和季节性。进一步分析ACF自相关，得到图2，该图证实了该数据却具有很强的序列性和弱平稳性。

平稳化处理

我们首先对财政收对数数据进行差分，因为差分前几项出现负值，我们采用滞后阶数对其进行差分，得到：

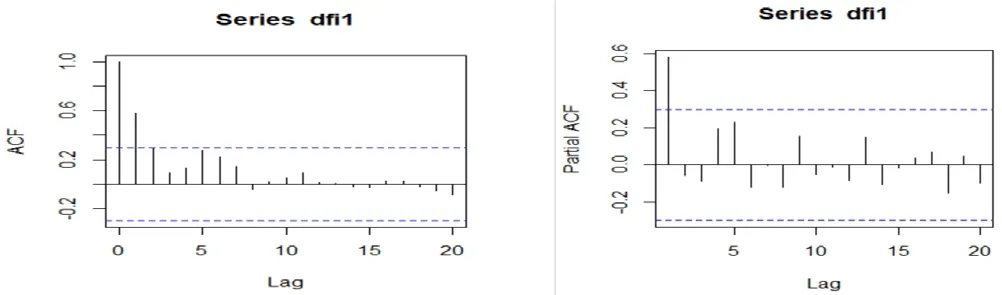
图3 差分后的对数序列的ACF、PACF

再进一步进行白噪声检验后发现，P值为8.32e-5,检验结果中P值小于5%，说明该序列通过平稳性检验。

模型的实证分析

建立模型

首先，根据对数序列的ACF建立AR（2）模型，通过比较两种模型，选出最佳的模型。

1.建立的AR（2）模型M1：

结果显示均值为0.0901，数值太小，因此将均值去掉；同时发现二阶时滞过小，移除后，建立AR（1）模型M2：

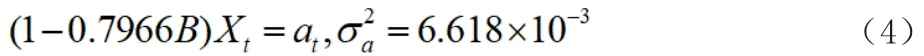
进行残差检验发现，M2模型的ACF在滞后5阶有一个显著非零，标准化残差仍有异常值。因此尝试ARMA(2,5)。第三次白噪声测试不显著，表明原始假设满足白噪声要求。

2.将数据代入，建立ARMA（1,5）模型M3：

因为MA模型中，3、4阶不显著，我们将MA的3、4阶去掉，得到模型M4：

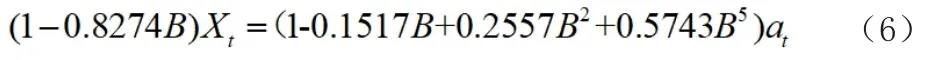
再次进行残差检测发现，标准化残差较M1模型变小。AR(1,5)残差的自相关基本通过白噪声检验。其中各个白噪声检验均不显著，说明原假设为符合白噪声要求。

模型的比较与选择

表1显示，M4模型比M1、M2、M3模型的AIC更小一些，并且标准差略大，因此选用M4模型。

?

模型的预测

根据建模步骤，对M4模型进行前5步预测，以5%为预测区间的置信水平，并对模型产生的预测误差进行了检验。白噪声测试用于检测延迟为1-20阶时，样本中的预测误差是否为非零自相关

检验结果为：X2=8.6824，df=20，p-value=0.9863

因此，残差具有良好独立性，检验通过，预测成立。继续推测未来5季度的预测值，其相对误差也均在7%左右波动。但具体误差为多大，需要与2019年第四季度以后的五个季度的实际对数值进行比较才得知。

图4显示，未来5季度财政收入可能略微下降，与我国政策和经济调控的大方向有关，财政收入可能对经济总量也造成一定影响。

结论

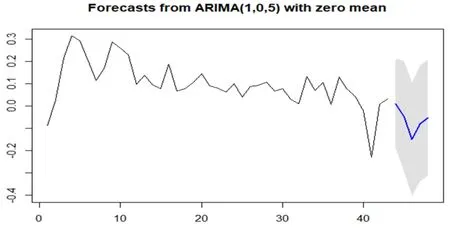
图4 预测图

本文对财政收入对数进行平稳性分析，将原始数据进行平稳化差分处理，使用ACF和PACF观察其平稳性，基本合理后开始建模。

预测选取最优M4模型，主要分以下两个部分：（1）仅预测五个值，目的是方便与接下来的短时间内几个季度的数据做比较，从而在更短时间内证明该模型的可行性。（2）对预测值的残差进行检验，判断预测是否成立，若不成立则要进一步对残差进行建模分析，再选择平稳模型，对该模型进行预测。