基于车身绕流的低雷诺数湍流模型改进研究1)

强光林 杨 易 陈 阵 谷正气 张 勇

(湖南大学汽车车身先进设计制造国家重点实验室，长沙 410082)

引言

汽车车身绕流是三维效应强、非定常、多尺度的复杂流动问题.目前由于缺少完备的实验手段能够准确测量汽车周边流场，揭示其机理，同时尚无足够的计算资源可对车身绕流进行直接数值求解，因此至今人们还没能全面、深入地掌握车身绕流规律[1]，并发展与之相适应的湍流模型.研究表明，不合理的湍流模型是数值求解误差的最主要来源，无法准确预测车身绕流转捩是常用湍流模型数值求解误差的主要原因[2].

本文通过梳理汽车绕流的流动机理及物理本质，分析汽车周边流动转捩的类型，将汽车各个复杂局部流动等效为近似简易模型.在此基础上，以LRNk-ε 模型[3]为原型，通过引入流线曲率因子及响应阈值改进了该模型对湍流耗散率的过强依赖性及全应力发展预测不足等问题，提升该模型对转捩的捕捉能力，最终获得一种改进的低雷诺数湍流模型.同时，引入约束大涡模拟思想，结合改进的低雷诺数湍流模型，构造适用于汽车绕流瞬态计算的转捩LRN CLES 模型.

1 汽车绕流局部近似模型

气流流经汽车车身，在汽车前端分离，形成主分离涡，主分离涡卷起一个包裹车头的椭球形漩涡，在顶面及侧面发生再附着现象.由于地面效应，汽车底部气流形成了特有的复杂边界条件，流动特性沿地面垂直方向变化剧烈.解决汽车外流场这种三维效应强、非定常、会流分离区多和涡结构复杂的流动问题，需深入剖析其局部流动[4].将汽车绕流模块化为典型局部流动，一方面有助于揭示汽车周边流动机理；另一方面使湍流模型的改进更具针对性.

本文将汽车绕流大致分为如下几类：汽车前缘底部类似于突缩流；后缘底部类似于半限制射流；车身几何外形突变的位置，如后视镜与A 柱间隙等类似于突缩、突扩流；前风挡与发动机舱拐角处类似于前台阶流动；车顶后缘几何断面突然扩张处，类似于后台阶流动；车顶部及发动机舱盖板处类似于平板流动.根据上述分类，分别建立平板流、前台阶流、射流、后台阶流及突缩流模型，构建合适边界条件，将车身绕流等效为5 类局部近似模型.

采用大涡模拟方法[5]对平板流、前台阶流、射流、后台阶流及突缩流的绕流机理进行数值研究,如图1，常用可实现的k-ε 湍流模型[6]计算结果被引入作为对比.对比分析发现：由于层流湍流转捩导致表面摩擦系数发生突变，LES 和可实现的k-ε 湍流模型在突变处有显著不同，因此可推测湍流模型对转捩的预测不足是造成计算偏差的主要原因.

图1 近似简易模型计算结果Fig.1 Computational results for approximate simple models

图1 近似简易模型计算结果(续)Fig.1 Computational results for approximate simple models(continued)

除可实现的k-ε 模型外，引入类车身平板流及类车尾后台阶流评估汽车绕流数值求解中常用湍流模型对转捩的模拟能力，标准k-ε 模型[7]、RNGk-ε 模型[8]、k-ω SST 模型[9]、RSM 雷诺应力模型[10]及LRNk-ε 模型[11]计算结果被引入作为对比，如图2 所示.Cf的走势图更加验证了湍流模型对转捩预测的不足是造成仿真偏差的主要原因.标准k-ε 模型及RNGk-ε 模型对层流湍流转捩的拟合偏差较大，这是由于以上两种模型引入了半经验式的壁面函数[12].虽然k-wSST 模型避免了壁面函数的经验式求解，但对边界层转捩依然无法准确预测.RSM 雷诺应力模型则耗费较大计算资源，且较难收敛.常用湍流模型中，对Cf预测最为准确的是LRNk-ε 模型，其低雷诺数边界层模拟机制与转捩较为相似，但对转捩的预测仍然存在一定偏差，特别是类车尾后台阶流动.

综上所述，对于汽车绕流各局部流动，转捩是决定流场发展的关键因素.因此，针对汽车绕流的数值模拟，提高湍流模型适应性的关键为增强其对转捩的预测能力.

2 构建改进的LRN k-ε 稳态湍流模型

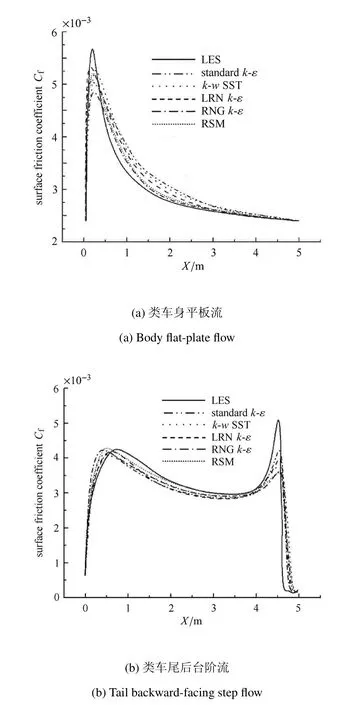
图2 常用湍流模型计算结果对比Fig.2 Comparison of the computational results of commonly used turbulence models

由于低雷诺数湍流模型将N-S 方程解析至壁面[13]，避免了经验式壁面函数的引入，有助于揭示近壁面区流动机理，并对转捩有巨大预测潜力，本文引入低雷诺数k-ε 湍流模型[11]，并对其进行转捩修正.全应力限制方法[14]使k-ω 模型获得了良好模拟转捩的能力，将此方法应用于LRNk-ε 湍流模型.同时，引入流线曲率因子提高模型对分离流转捩的模拟能力，构建改进的LRNk-ε 湍流模型.

2.1 基于全应力限制方法的湍流耗散率推导

Jones 和Launder[11]提出的基于时均N-S 方程的低雷诺数湍流模型如下式所示

式中，μ 为分子黏性系数，ρ 为流体密度，μt是湍流黏度，常数η0=4.377,β=0.012，Cμ=0.09，f1=1，cε2=1.92，时均应变率Si j通过cε1引入以处理高应变率及弯曲流.ReT是湍流雷诺数.

扩散系数中的分子扩散系数及湍流扩散系数反映了分子黏性的影响；附加项2μ(∂k1/2/∂xi)2被引入以反映黏性底层中湍动能耗散的各向异性；附加项2(μμt/ρ)()2被引入以使湍动能k的计算结果与某些实验测定值更相符.

由于常用湍流模型对流动分离预测的不足表现为：过晚模拟出分离及过早模拟出再附着，相关实验及DNS[15]结果也证实了这种不足[14].针对以上问题，引入全应力限制方法，消除湍流模型对湍流耗散率的过强依赖性，避免了由原始湍流模型对湍动能耗散率的过低估计带来的负面影响，具体改进过程如下.

由湍动能k的表达式

综合考虑全应力及雷诺应力的影响，可知

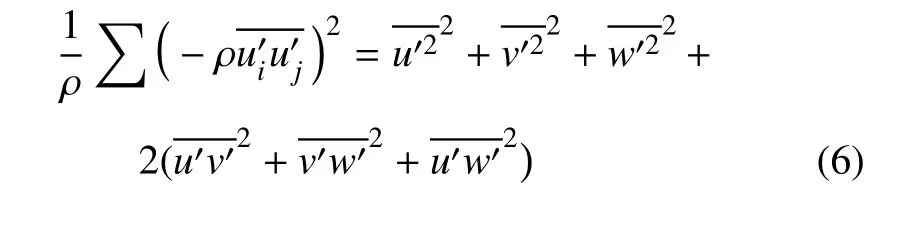
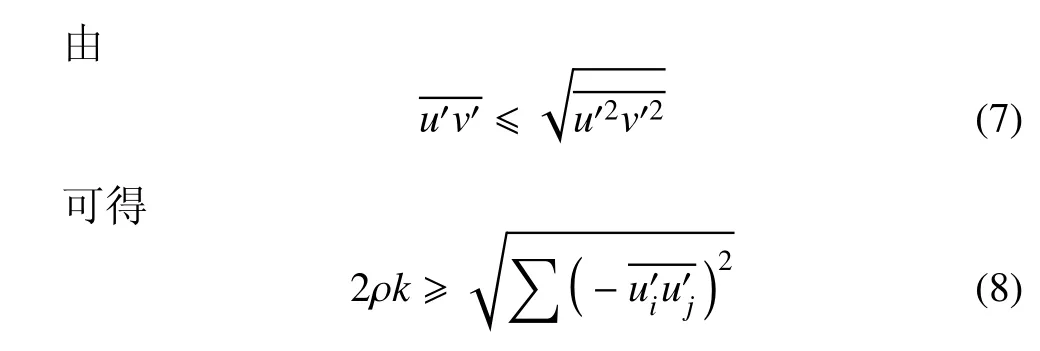
该式可限制额外湍流应力的生成.

由Boussinesq 假设可知

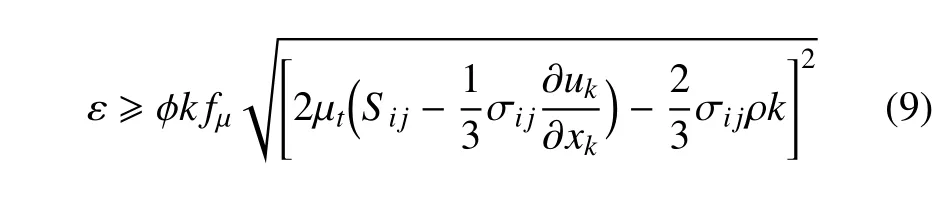
进一步推导可得

综上所述，湍动能耗散率应被约束如下

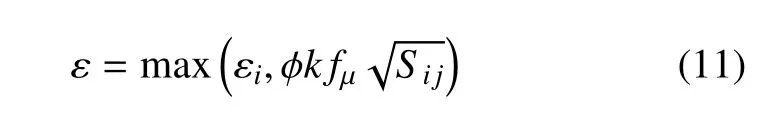
ε0由原始湍动能耗散率输运方程得出，k由原始湍动能耗散方程得出，对于大多数流动，φ 取2.5 可保证湍流模型对转捩的良好预测能力.这项改进未引入额外输运方程，可由原始湍流模型直接计算获得，对湍流模型在湍流充分发展区的计算结果影响较小.

2.2 考虑流线弯曲效应的湍流黏度构造

全应力限制方法可使LRNk-ε 模型获得良好预测转捩的能力，然而对于分离流转捩，还需发展更为有效的方法.相关实验及DNS计算结果表明[14]：在流动分离区域，即使仅存在极小分离泡[16]，扰动也会被迅速放大，湍动能则会迅速增长.随着湍动能的较快增长，即使当地雷诺数较低，流动也会迅速发生转捩.因此，要提高湍流模型对分离流及分离流转捩的模拟能力，须构造对流动分离较为敏感的感应量，流动分离通常伴随着高弯曲率，因此，弯曲率被引入作为感应量.

流线s的弯曲率Cs为

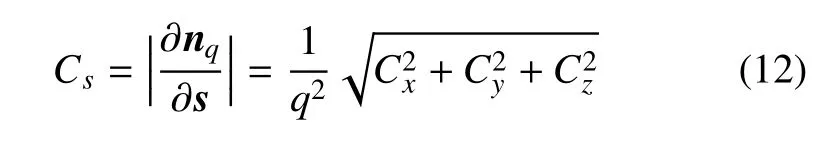
式中，q为速度矢量，q=(u,v,w)；q为速度标量q=，矢量nq被定义为nq=(u/q,v/q,w/q)；Cs代表三维流线曲率的标量值，也是涡半径的倒数值，可用于表征涡的长度尺度.Cs在3 个方向上的弯曲应变率分量分别为

构造一个关联Cs的无量纲量Sl，将Cs引入湍流黏度，Sl可表示为

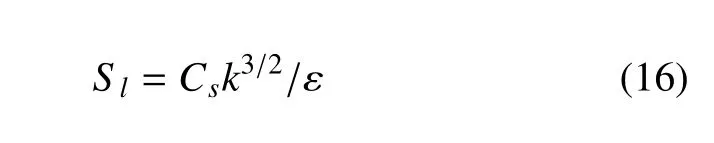
Sl的物理意义是湍流长度(时间)尺度与漩涡长度(时间)尺度的比值，也可作为湍流与漩涡之间的生成项与湍流耗散项的比值.

通过参数α，湍流黏度被表征为关联Sl的方程

经计算对比发现，χ 应与Rl在同一数量级，取为0.1 较合适，C0取为10 较为合适.

以上改进中，流线曲率被无量纲化为Sl，Sl则被用于构造α.流动雷诺数较低时，ReT较小，当层流边界层分离，Sl迅速增大，α 将促发转捩，使得模型具备模拟分离流转捩的能力.一旦层流转捩为湍流，ReT剧增，Sl的影响就微乎其微了.流线曲率的引入结合全应力限制方法可得出能准确预测转捩的改进的LRNk-ε 湍流模型，这个模型不仅能准确预测分离流转捩[17]，还可准确模拟自然转捩及旁路转捩[18].

3 构建转捩LRN CLES 瞬态湍流模型

汽车绕流的瞬态数值求解对计算资源的消耗巨大，特别是近壁面附近[19].混合RANS/LES 方法[20]则可针对不同的流动问题，引入与之相适应的RANS 模式[21].考虑到近壁面处LES 模式的巨大计算资源消耗，本节对RANS/LES 混合模型中的RANS 模式进行转捩修正.考虑到发展较为成熟的CLES 模型[22]能较好地模拟圆柱绕流转捩，将其引入以处理汽车绕流瞬态问题.同时，汽车绕流为高应变率及大曲率流动，存在较多的流动分离，转捩现象更为复杂，将改进的LRNk-ε 模型引入以构造约束大涡模拟RANS 区域的C-SGS 模型[23]，进一步提高对转捩的捕捉能力，最终可获得转捩LRN CLES模型.

3.1 约束亚格子应力模型建立

由于汽车绕流属于低马赫数流动，引入不可压缩流的大涡模拟控制方程

其中，顶标～代表低通过滤，通常以Δ 为过滤尺度；ρ 为流体的密度；为滤波后大尺度涡的速度；为滤波后的压力；υ 为运动黏性系数；τij为亚格子尺度应力，代表过滤后的小尺度涡对大尺度涡的影响，可表示为

基于大涡模拟求解的关键为亚格子模型[24]，其中应用最为广泛的是由Lilly 及Liu 提出的DSLM 模型[25]，由于DSLM 模型不能较好的处理近壁面流动，此处引入约束大涡模拟思想，对RANS 区域C-SGS 模型的推导如下.

根据RANS 及LES 控制方程在数学上的高度一致性，RANS 区域总雷诺应力Ri j、总亚格子应力的时均值〈τij〉及滤波后的雷诺应力应存在以下关系

符号〈〉 代表相应物理参量的时均值，Ri j可由RANS 模化为，则通过直接求解N-S 方程得出

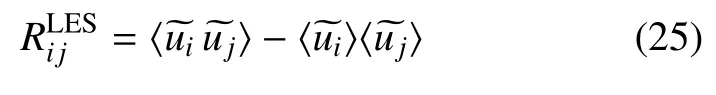
由此可得

总亚格子应力可分解为时均值〈τij〉及脉动值(τij)′

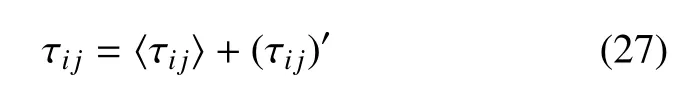
(τij)′可由Lilly 及Liu 提出的DSLM 模型模化为()′

由DSLM 模型确定，由此可得RANS 区域;CSGS 应力为

C-SGS 模型仅用于求解近壁面区流动或者总雷诺应力可由RANS 模化的流动区域，LES 模型则对其余流动区域直接求解.C-SGS 模型的准确性很大程度上取决于，的准确性又依赖于RANS 模型，针对汽车绕流问题，RANS 模型的准确性则取决于其对转捩的预测能力.

3.2 基于改进的LRN k-ε 模型的CLES 建立

针对汽车绕流问题，C-SGS 模型主要作用于近壁面区，该区域内可由DSLM 模型直接计算，Ri j则由第二节提出的能准确预测转捩的改进的LRNk-ε 模型进行计算，计算过程如下

式中，μt为湍流黏性系数；常数Cμ=0.09，Φ=2.5；Si j为时均应变率；ε0由原始湍动能耗散率输运方程得出，k由原始湍动能输运方程得出

其中C0=10，Cs代表三维流线曲率的标量值，也是涡半径的倒数值，可用于表征涡的长度尺度，Cs由无量纲量数Sl引入湍流黏度.

4 改进模型验证与分析

4.1 风洞实验设置

实验采用1/3 缩比的汽车模型如图3 所示，实验遵循相似准则.风洞试验段尺寸为2.5 m×3 m×17 m，可进行最高1:3 的缩比汽车模型实验，湖南大学HD-2 风洞[26]设计最大风速为58 m/s，可满足雷诺数相似原则，进入“自模拟”状态.

4.2 改进的LRN k-ε 稳态湍流模型验证分析

本节将具备主流三厢轿车造型的某实车模型及其HD-2 风洞实验数据引入以验证改进的LRNk-ε 模型及标准化数值求解体系.

图3 试验模型Fig.3 Test model

4.2.1 网格类型选择

引入课题组前期某最简实车模型风洞实验数据[27]，基于改进的LRNk-ε 模型，分别利用非结构网格及结构网格进行仿真分析，如图4 所示.由表1结果可知，即在不考虑模型网格划分难易的情况下，非结构也能较快收敛，且得到较为准确的计算结果.因此，后续实车仿真模型采用非结构网格划分.

图4 最简实车模型的非结构(左)与结构网格(右)Fig.4 Unstructured(left)and structural grid(right)of the simplest automobile model

表1 结构与非结构网格计算结果Table 1 Computational results based on structural and unstructured grids

4.2.2 模型简化及仿真参数设置

本实验采用的实车模型较为复杂，省略前格栅、轮毂、门把手、灯组、尾气管、B柱及车底细节，保留其余特征.简化后的计算模型尺寸如图5 所示，长1588 mm、宽643 mm、高505 mm，最小离地间隙50 mm.

综合计算效率及阻塞效率，选取计算域高为5 倍模型高度，宽为6 倍的模型宽度，长为12 倍模型长度(车前端距入口3 倍车长，后端距出口8 倍边界长度)[28].入口边界设置为速度入口，来流速度设置为30 m/s，湍流度为0.028 0，出口边界设置为压力出口，相对压力为零.计算域顶部及两侧壁面设置为对称边界，计算域底部设置为移动壁面，汽车模型壁面设置为固壁无滑移壁面，选取改进的LRNk-ε 和可实现的k-ε 模型进行仿真计算.具体的仿真计算域及边界条件设置如图5 所示.控制方程离散格式设置为二阶迎风格式，压力与速度耦合设置为SIMPLE 隐式求解法.

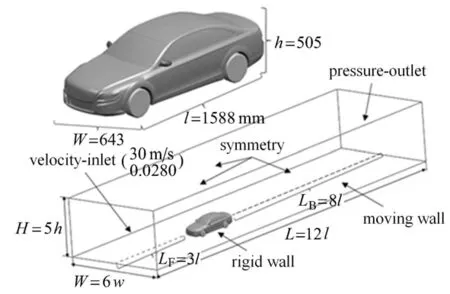
图5 模型试验尺寸和仿真计算域及边界条件Fig.5 Model size,simulation computational domain and boundary conditions

4.2.3 网格无关性验证

仿真采用非结构网格划分，分别设置3 种网格划分策略，验证网格无关性.流动急剧变化部位被加密，边界层取10 层，增长率为1.1，经数次调整第一层网格高度，大部分模型表面y+值均分布于合理范围内，此时第一层网格高度为0.012 mm.计算在8 个8 核CPU、64GB 内存的DELL Power 服务器上进行计算.

表2 不同网格阻力系数和计算时间Table 2 Drag coefficient and computational time based on different grid numbers

综合考虑表2 中计算结果的误差和收敛时间，选择第2 种网格划分策略，网格划分情况如图6所示.

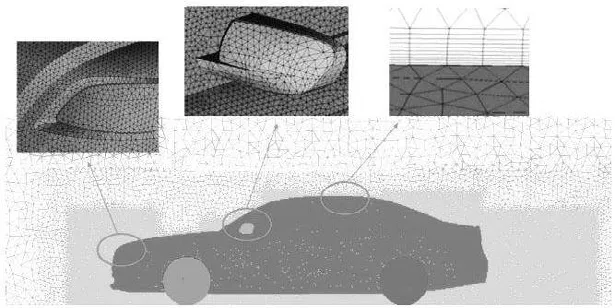
图6 该实车模型计算域网格Fig.6 Model computing grids

4.2.4 计算结果分析

收敛耗时25 h.保证其他求解条件不变，基于可实现的k-ε 模型的计算结果及HD-2 风洞试验数据被引入作为对比.计算及实验所得该实车模型的气动阻力系数Cd值及气动升力系数Cl值如表3 及图7 所示.

表3 气动阻力系数及气动升力系数(β=0°)Table 3 Aerodynamic drag coefficient and aerodynamic lift coefficient(β=0°)

由图表可知，本文提出的改进的LRNk-ε 模型可较好的计算该模型的气动阻力及气动升力，与风洞试验结果误差较小，特别是对汽车气动升力的计算，较常用的可实现的k-ε 模型有较大提升.

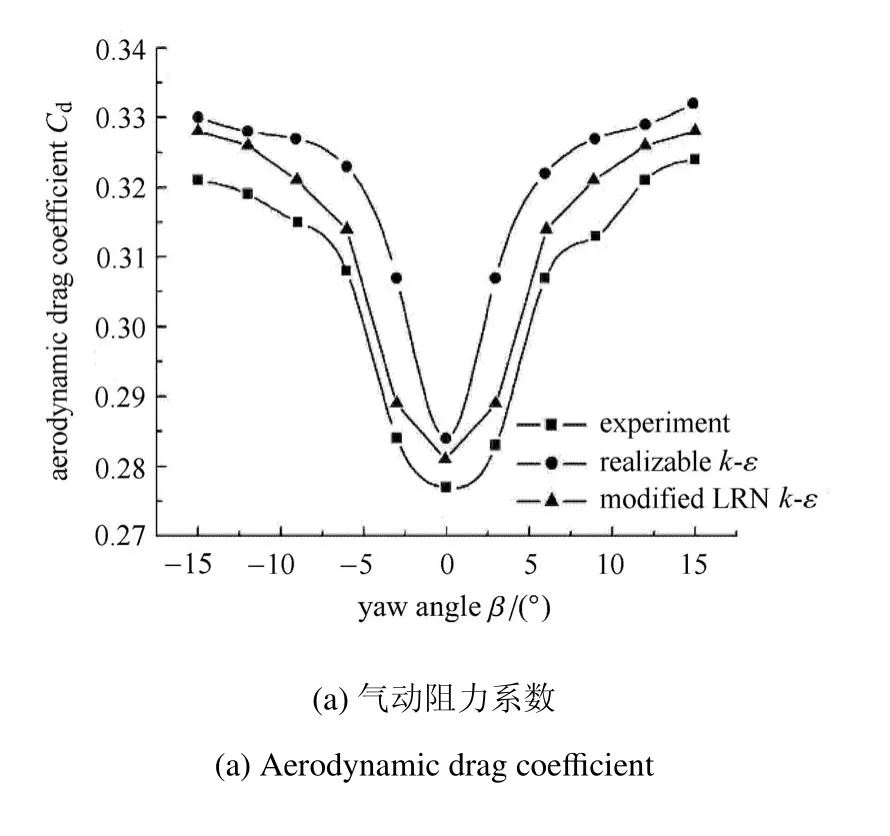
图7 实车模型气动阻力与升力系数Fig.7 Aerodynamic drag and lift coefficient of the model

图8～图11 分别表示改进的 LRNk-ε 模型计算所得表面静压分布、车头及车尾处流场分布，该结果与风洞试验较为吻合.由该实车模型表面压力分布图8 及车头流线图9 可知，气流最先到达汽车头部，受到阻滞作用形成驻点，产生较大正压区，并贴附汽车表面形成边界层.之后，气流在行驶至发动机舱盖板的过程中，受正压梯度影响，与前台阶流较为相似.气流流至汽车尾部的气流边界层则类似于后台阶流.本文汽车尾部过渡曲率较小，逆压梯度作用较小，边界层行驶至汽车尾端才脱离物面，并形成自由剪切流，在尾部形成漩涡，之后汇入尾流，实验与仿真在汽车尾部均出现两个漩涡，实验对比结果较好.图10 和图11 中可以看出实验与仿真之间仍然有一些偏差，一方面是由于实验条件的限制，实验与仿真保证了相似准则，但无法确保完全一致，并且实验会受到不可控的一些外部因素的干扰；另一方面是由于本文提出的改进的模型仍然基于一部分经验公式，因此还需经过多个算例进行验证，发现其不足，并进行修正，提高其普适性.

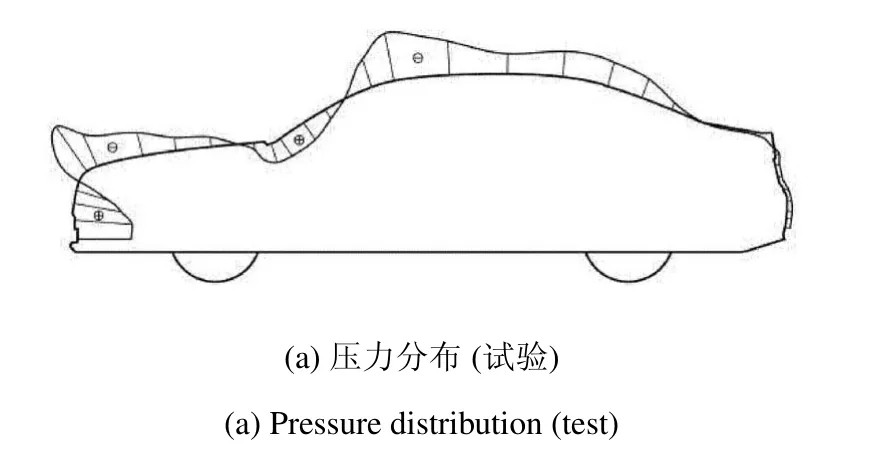
图8 表面压力分布Fig.8 Surface pressure distribution

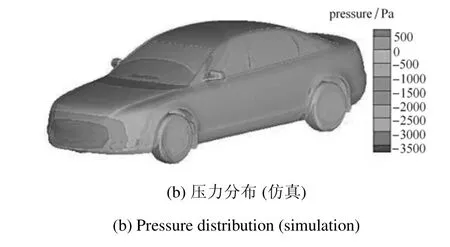
图8 表面压力分布(续)Fig.8 Surface pressure distribution(continued)

图9 车头流线图Fig.9 Streamline diagram at the head

图10 车头涡量图Fig.10 Vorticity diagram at the head

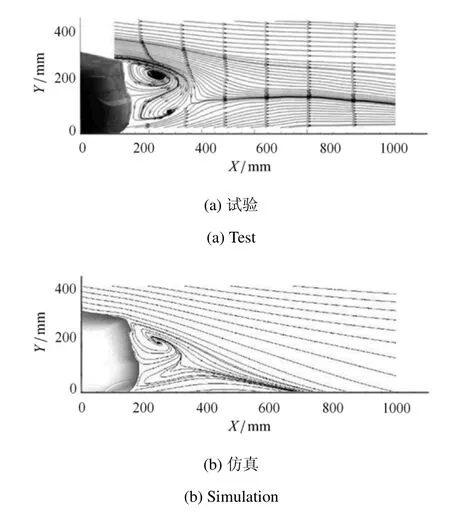
图11 车尾流线图Fig.11 Streamline diagram at the tail

4.3 转捩LRN CLES 瞬态湍流模型验证分析

汽车风振噪声产生于气流的脉动压力，具有较强的瞬态特性，是典型的瞬态汽车绕流问题.汽车周边脉动压力的数值求解对湍流模型要求较高，本节引入某款轿车进行的实车道路试验验证转捩LRN CLES 模型对汽车瞬态绕流的求解能力.

4.3.1 模型简化及仿真参数设置

简化后的计算模型如图12 所示，具体尺寸如图13，长4682 mm，宽1879 mm，高1624 mm，最小离地间隙150 mm.

对车辆进行仿真的外部计算域为长方体，参数设置和4.2.2 节一致.入口边界设置为速度入口，来流速度设置为30 m/s，湍流度为0.024 3，出口边界设置为压力出口，相对压力为零.计算域顶部及两侧壁面设置为对称边界，计算域底部(即地面)设置为移动壁面，汽车模型壁面设置为固壁无滑移壁面，与试验相对应，将左后侧窗设置为Int Wall，模拟该侧窗的开启环境.选取转捩LRN CLES 模型进行仿真计算.具体的仿真计算域及边界条件设置如图13 所示.

对于瞬态求解，控制方程离散格式设置为边界中心差分格式，压力与速度耦合设置为PISO 隐式求解法.

图12 汽车风振噪声数值计算模型Fig.12 Numerical calculation for buffeting noise of the automobile model

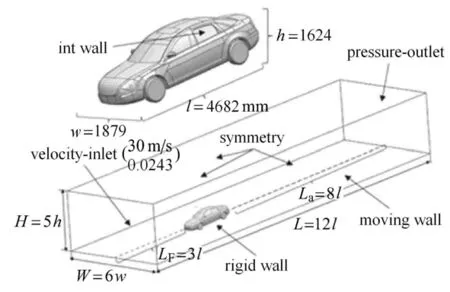
图13 模型尺寸和计算域及边界条件Fig.13 Model size,calculation domain and boundary conditions

4.3.2 网格划分

采用非结构网格划分后，该实车模型模拟网格总数约为2800 万，网格设置与4.2.3 节情况相同，网格划分情况如图14 所示.

4.3.3 计算结果分析

此瞬态计算时间步长取为1.0×10-4s，每个时间步内迭代计算20 次.由道路实验结果可知，声压级(SPL)第一个阶次峰值出现的频率为17.6 Hz，因此周期约为0.056 8 s，为实现充分瞬态效应，取流动总时长为2.1 s.计算总耗时32 d 3 h.

图14 该实车模型气动噪声计算域网格Fig.14 Aerodynamic noise computing grids

本课题组前期研究中的SAS计算结果[29]被引入作为对比.计算结果如图15 所示，计算所得前3 个阶次声压级峰值及其出现频率如表4 所示.由图表可知，转捩LRN CLES 模型及SAS 模型[30]计算所得声压级峰值均低于实验值，这是由于数值计算仅考虑了计算域流场环境，而道路实验受诸多周边环境影响，背景噪声较大.但转捩LRN CLES 模型与实验结果更为接近.验证了转捩LRN CLES 模型良好的瞬态性能.

图15 仿真计算和实验声压级Fig.15 SPL of the simulation and test

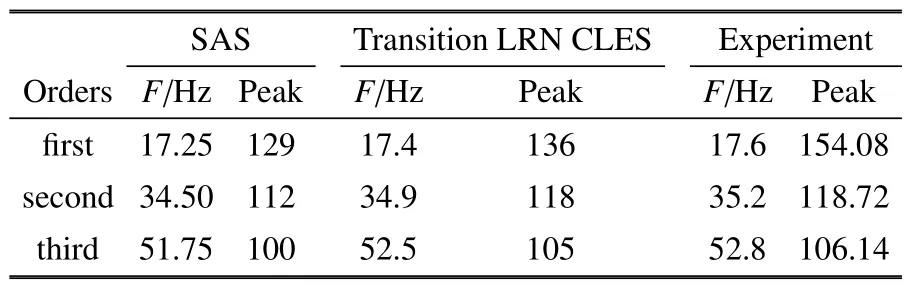
表4 声压级峰值频率Table 4 Peak frequency of SPL

5 结论

本文首先通过典型局部流动对汽车绕流机理进行深入分析，研究发现转捩是决定流场发展的关键因素.针对汽车绕流稳态及瞬态求解，分别提出了一种能够准确预测转捩现象的改进的LRNk-ε 及转捩LRN CLES 模型，并将其应用于实车模型绕流的数值研究以验证其准确性.

通过对某实车气动力及风振噪声的数值研究，并与HD-2 风洞试验及实车道路试验进行了对比分析，结果表明：相同网格条件下，相对于常用的湍流模型，基于本文提出的改进的LRNk-ε 及转捩LRN CLES 湍流模型的标准化高精度数值求解体系能够更准确模拟复杂实车的绕流特性，特别是对气动升力的数值计算，精度高于常用湍流模型.