基于Navier-Stokes 方程残差的隐式大涡模拟有限元模型1)

陈林烽

(江苏科技大学,江苏镇江 212003)

引言

作为湍流数值模拟方法的一种,大涡模拟方法(large eddy simulation,LES) 在未来的工业应用中具有极大的潜力.大涡模拟方法的主体思想是针对湍流不同尺度涡的不同特点,弓入介于大涡尺度和小涡尺度之间的滤波器对Navier-Stokes 方程进行过滤,保留滤波器宽度以上的大涡特征,对所保留的大尺度涡结构进行直接模拟,对小尺度涡结构采用不可解尺度模型模拟[1-2].相比于直接数值模拟(Direct numerical simulation,DNS),它过滤了小尺度信息,计算时网格数量需求更低,计算耗时变得更短;相比于雷诺平均方法(Reynolds average Navier-stokes,RANS),它通过调节网格尺寸,可以保留不同程度的大尺度信息,因此除了平均尺度之外,它还能计算得出不同程度的大尺度旋涡[3-4].在过去的几十年里,大涡模拟方法的研究一直是计算流体力学科研学者们的重点关注问题[5-6].

大涡模拟方法的核心问题是构建不可解尺度(不可解尺度) 模型.自大涡模拟方法提出以来,已经有多种不可解尺度模型被提出.Smagorinsky[7]在1963 年提出了涡黏形式的不可解尺度模型,随后Lilly[8]利用湍动能谱确定了Smagorinsky 模型系数.该模型最早应用于大气工程中的大涡模拟计算.实际使用过程中发现该模型在近壁区耗散过大,无法捕捉层流到湍流的转捩过程.Bardina 等[9]提出流动中可解尺度脉动向不可解尺度脉动输运的动量由可解尺度脉动中的最小尺度部分产生,并且可解尺度脉动的最小尺度脉动速度和过滤掉的小尺度脉动速度相似,从而提出尺度相似模式.该模型在实际应用时湍动能耗散太小,往往导致计算发散.Germano 等[10]提出二次过滤并假设二次过滤后的亚格子应力等于粗、细网格上的亚格子应力差,从而得出动态不可解尺度模式.动态确定模型系数时,需要对流场信息进行统计平均.对于湍流脉动存在统计均匀方法,通常采用空间统计平均来代替系综平均.对于没有统计均匀方向的流动,Maneveau 等[11-12]提出沿质点轨迹平均的动态确定模式系数方法.实际计算结果表明,对于规则几何边界处的湍流,动态不可解尺度模式可以得到较好的计算结果.对于不规则几何边界处的湍流,二次过滤计算动态不可解尺度模型系数时往往会出现错误.随后,Nicoud 等[13]提出了壁面自适应不可解尺度模型(WALE).

随着大涡模拟方法的发展,Hughes 等[14]在有限元方法的框架下将多尺度方法应用于大涡模拟方法.在有限元的框架下,假设Navier-Stokes 方程的解的形函数由可解尺度和不可解尺度形函数叠加组成,弓入对应的权函数,将Navier-Stokes 方程的有限元变分形式分解为可解尺度和不可解尺度系统.Hughes 等[14]将可解尺度进一步分解为大尺度与小尺度,采用传统的Smagorinsky 不可解尺度模型模拟不可解尺度,然后将不可解尺度模型仅作用于小尺度(或大尺度).该方法无需使用过滤函数对Navier-Stokes 方程的变量进行过滤,通过对形函数进行尺度分解实现解的尺度分解.不可解尺度模型仅作用于可解尺度中的小尺度(或大尺度),更贴近湍动能输运规律.Hughes等[15-16]通过各向同性湍流和槽道湍流的数值实验验证了基于有限元多尺度概念的大涡模拟方法较传统的大涡模拟方法更为准确,证实了该方法的未来潜力.

Hughes 等[17]在将多尺度方法运用于对流扩散方程和Stokes 方程时,借助Green 函数求出了不可解尺度系统的解析解.通过将不可解尺度的解析解代入到可解尺度系统后,可以使用较少的网格数量计算得到理想的数值模拟结果.根据不可解尺度的解析解形式,可以发现不可解尺度是可解尺度方程残余量的函数.对于Navier-Stokes 方程,鉴于方程的复杂性,无法通过不可解尺度系统求得解析形式.在Hughes 等[18-22]的工作的启发下,本文将根据Navier-Stokes 方程的不可解尺度系统建立基于大尺度方程残差的不可解尺度模型,然后将其代入Navier-Stokes方程的大尺度系统并直接求解之得到Navier-Stokes方程的大尺度解.

1 数值方法

本文将采用有限元方法对流体控制方程Navier-Stokes 方程

进行离散求解[23].令W={w,q} 为对应于Navier-Stokes 变量U={u,p}的权函数,则Navier-Stokes 方程的有限元变分形式可写为

式中(,)Ω表示前后两个变量乘积在计算域内部的有限元单元内的积分,Ω 表示计算域内部空间.

2 多尺度方法

2.1 多尺度分解

鉴于湍流流动内存在多种尺度的旋涡,可以将Navier-Stokes 方程的解看成是大尺度解和小尺度解叠加而成(如图1),即

相应地,可以将权函数分解为大尺度和小尺度

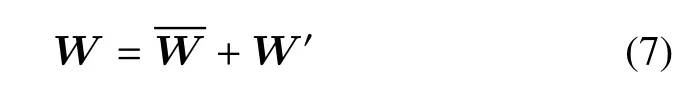
将式(6)和式(7)代入Navier-Stokes 方程的变分形式(3)中可以得到分别投影到大尺度权函数和小尺度权函数的两组方程[24-27]

图1 Navier-Stokes 方程解的尺度分解示意图Fig.1 Sketch of scale decomposition of solution to Navier-Stokes equations

这里,将式(8)称为大尺度系统,将式(9)称为小尺度系统.其中

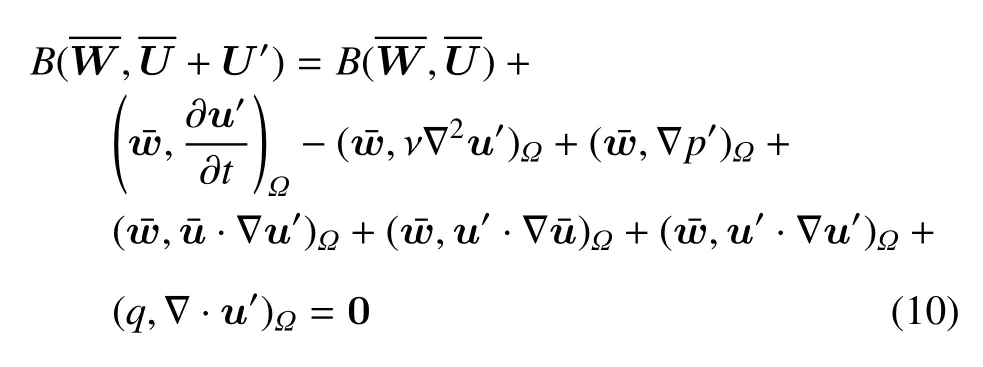
式中第二、三和四行为小尺度相关项.通常情况,∂u′/∂t和ν∇2u′为较小值,于是式(10) 第二行的前两项可忽略[28].为了避免在方程中出现,∇u′和∇p′项,对式(10)中的对应项采用分布积分[26],于是

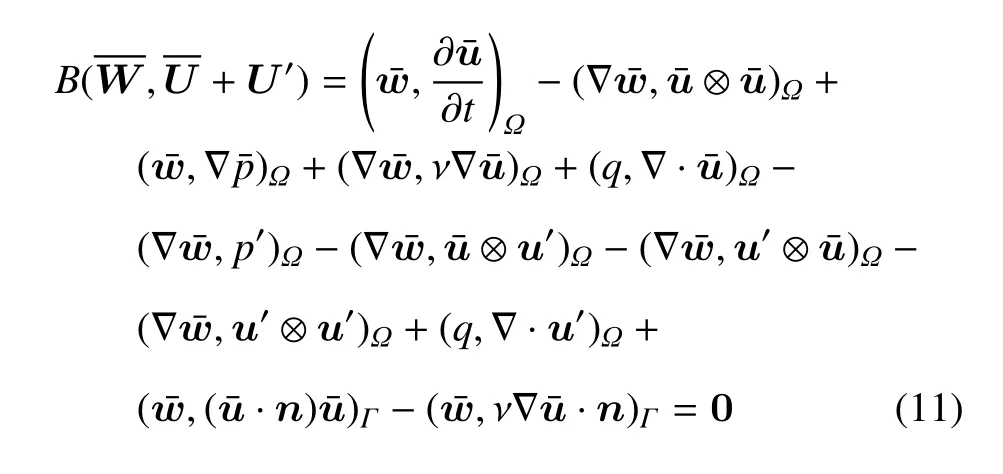
对比于传统大涡模拟方法的亚格子应力包含的Leonard,Corss 和Reynolds 应力项,式(11)中包含有对应项[30]:

值得注意的是,在以上大尺度方程的推导过程中还没有使用任何模型.

对于大尺度方程式(11),如果能找到{u′,p′} 的精确表达式,便可以通过求解式(11) 得到精确的大尺度解.式(11)与式(9)相互耦合,于是可以试图通过式(9)去找到{u′,p′}表达式.鉴于式(9)与式(11)同样复杂,以下将通过分析式(9) 的具体形式,去建立{u′,p′}的近似模型.

2.2 不可解尺度模型

将式(9)展开后可以得到

将式(12)的大尺度和小尺度项进行整理得到

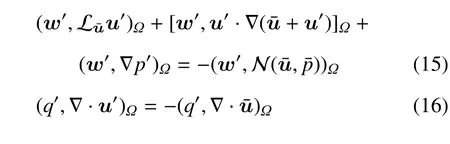
注意到式(15) 和式(16) 右边为大尺度相关项.式中∇·和N()分别为连续性和Navier-Stokes 大尺度方程残差,即

于是,式(15)可简化为

假设∇p′为极小量,式(15)可以再次简化为

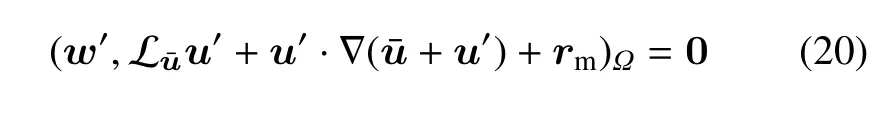
其等效于

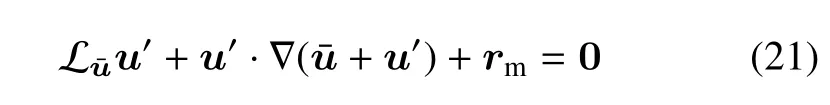
忽略u′·∇()的影响,小尺度u′的方程最终为

式中c1,c2和c3为常数,G为单元局部坐标与全局坐标之间的转换系数矩阵

ξ为单元局部坐标,x为全局坐标,G:G表示矩阵G的双点积.将式(22)代入式(21)得

于是解得

由式(19)和式(16)并忽略式(19)中u′·∇(′)的影响可以得到

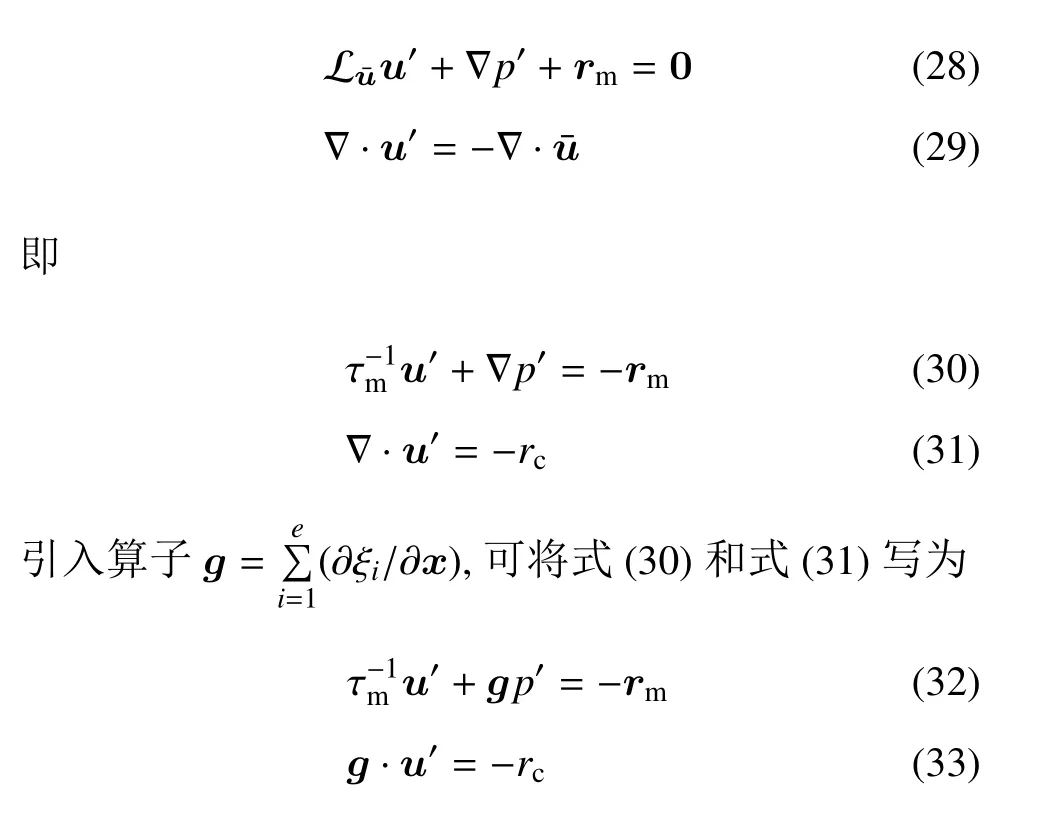
式(32)两边同时点乘gτm得到

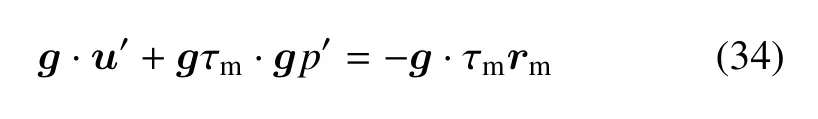
将式(33)代入式(34),在计算p′时假设rm已经满足rm=0,于是得到p′的模型为

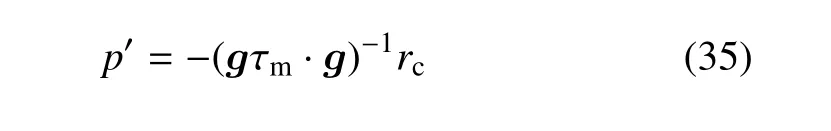
令τc=(gτm·g)-1,则

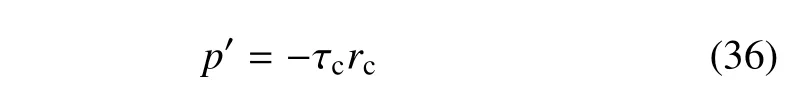
将式(27)和式(36)代入大尺度方程(11)可以得到

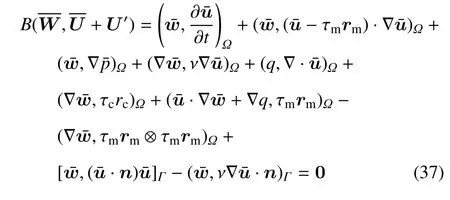
注意到,此时大尺度方程仅包含大尺度变量,即方程得到封闭.

3 时间推进方法

在数值模拟时,将直接去求解大尺度方程式(37).这里采用Jansen 等[34]提出的generalized-α 方法进行时间步推进.以及将介绍generalized-α 方法应用在式(37)的详细细节.

将a定义为{}的节点系数,˙a定义为a的时间倒数.于是,式(37)离散后可整理为

式中A和B分别为式(37)离散系统整理后和a的系数矩阵.弓入generalized-α 得到

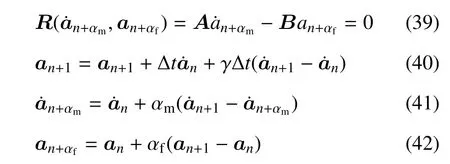
式中

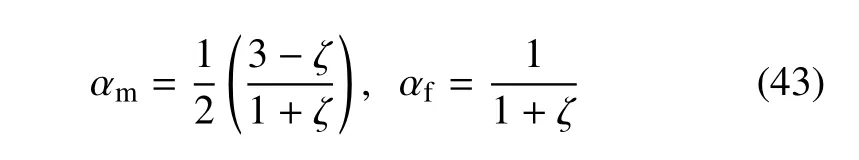
其中ζ=0.5 以确保时间推进精度为二阶精度和无条件收敛

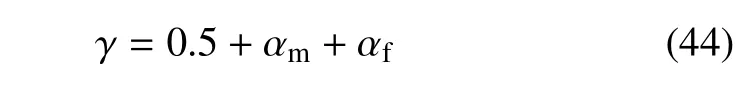
在每一个时间步上采用迭代方法求解式(38).假设

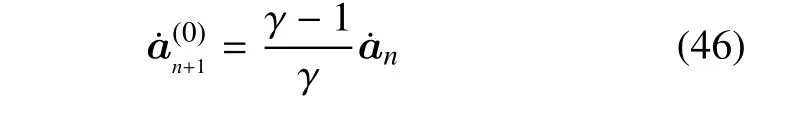
将式(45)和式(46)代回式(41)和式(42),再将得到的和an+αf代入式(39),并对其使用牛顿迭代

4 数值验证

4.1 算例设置

本文针对Reτ=180 的槽道湍流问题,对基于Navier-Stokes 大尺度方程残差的大涡数值模拟方法及其自编程序[35-37]做出验证.其中Reτ=uτδ/ν,uτ为壁面摩擦速度,δ 为槽道的半宽度,ν 为流体运动黏性系数.流场的计算域为Lx=2δπ,Ly=2δ,Lz=4δπ/3(如图2 所示).

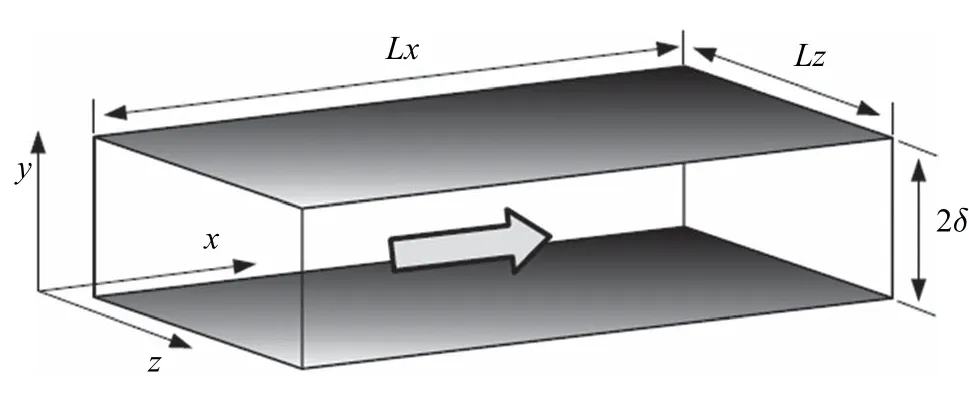
图2 槽道流示意图Fig.2 Sketch of channel flow

计算域的网格划分采用六面体网格(如图3 所示),在流向(x)与展向(z)方向上采用均匀网格,在垂向(y)方向采用双向正切函数

对壁面附近网格进行加密.本文分别使用32×32×32和48×48×48 个单元的两种网格对流场进行数值模拟.网格的详细参数见表1,表示壁面单元的无量纲尺寸.

图3 48×48×48 个六面体单元组成的网格示意图Fig.3 Mesh sketch of 48×48×48 hexahedral elements

表1 计算参数Table 1 Computation parameters

三维单元上的形函数以及有限元权函数均使用双线性(bilinear) 函数,即形函数由每一个方向上的线性函数相乘得到,如(1-ξ)(1-ψ)(1-ζ).图4 为垂向上由双向正切函数得到的非均匀网格单元上的线性形函数示意图.

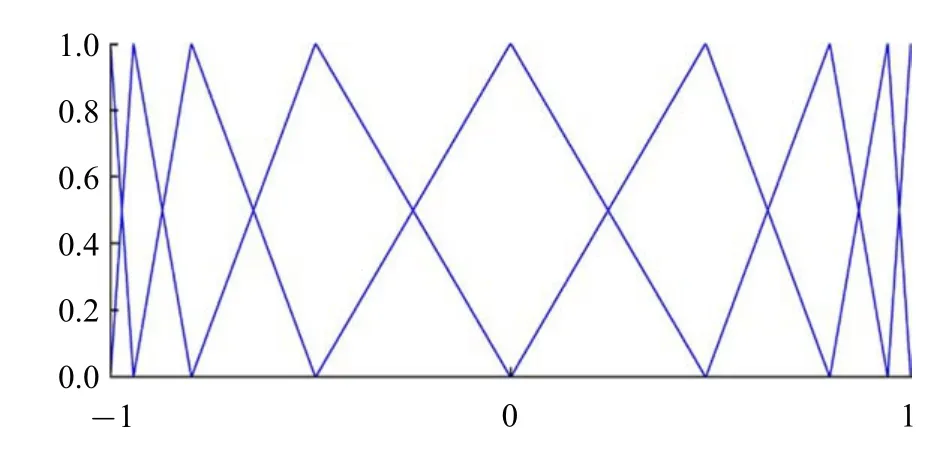
图4 垂向线性形函数示意图Fig.4 Sketch of linear shape functions in the normal direction

数值模拟中,流向和展向采用周期性边界条件,上、下固壁处使用无滑移边界条件(uwall=0).流向进出口之间给定一个恒定的压力差来维持流体流动,并在入口处给定一个压力参考值作为压力的边界条件.对离散的式(37)使用gernerzlized-α 后,可以得到式(47)的线性方程系统.这里,采用基于ILU 的GMRES 迭代算法并行求解式(47)的线性方程系统.图5为使用48×48×48 个单元计算得到的瞬时流场流向速度云图.从入口的截面可以看到,在壁面附近有很明显的展向旋涡.

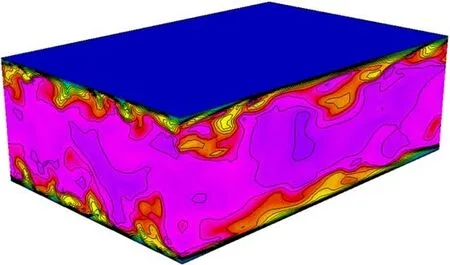
图5 48×48×48 个单元瞬时流场流向速度云图Fig.5 Instantaneous contours of streamwise velocity using 48×48×48 elements

4.2 结果与分析

在流场稳定以后,对20 000 个时间步的流场数据进行了统计计算,得到流场的平均速度和脉动速度均方根值.

图6 为流向平均速度在垂向方向(y+)的分布图,〈U〉 表示在x和z方向上的空间及时间综合平均统计量,y+=uτy/ν=yReτ.图中分别给出了Jimenez的直接数值模拟和32×32×32,48×48×48 个单元的Smagorinsky 模型大涡模拟有限差分[3-4]和本文的计算结果.可以看出,在壁面附近(y+＜ 15),本文所用方法的计算结果与DNS 数据匹配的很好,而Smagorinsky 模型过大的耗散导致该区域的计算结果低于DNS 数据; 在对数率区(30 ＜y+＜50) 和黏性外层(y+＞50),本文的计算结果略大于DNS 计算结果.该区域的平均速度随着网格数量增多变得更接近DNS 数据.根据这一结果,可以判断该模型在32×32×32,48×48×48 个单元的计算中所提供的湍动能耗散略偏小.

图6 流向平均速度在垂向方向上的分布Fig.6 Mean streamwise velocity(〈U〉)profiles against y+

图7 给出了脉动速度均方根值(urms) 在垂向方向的分布图,

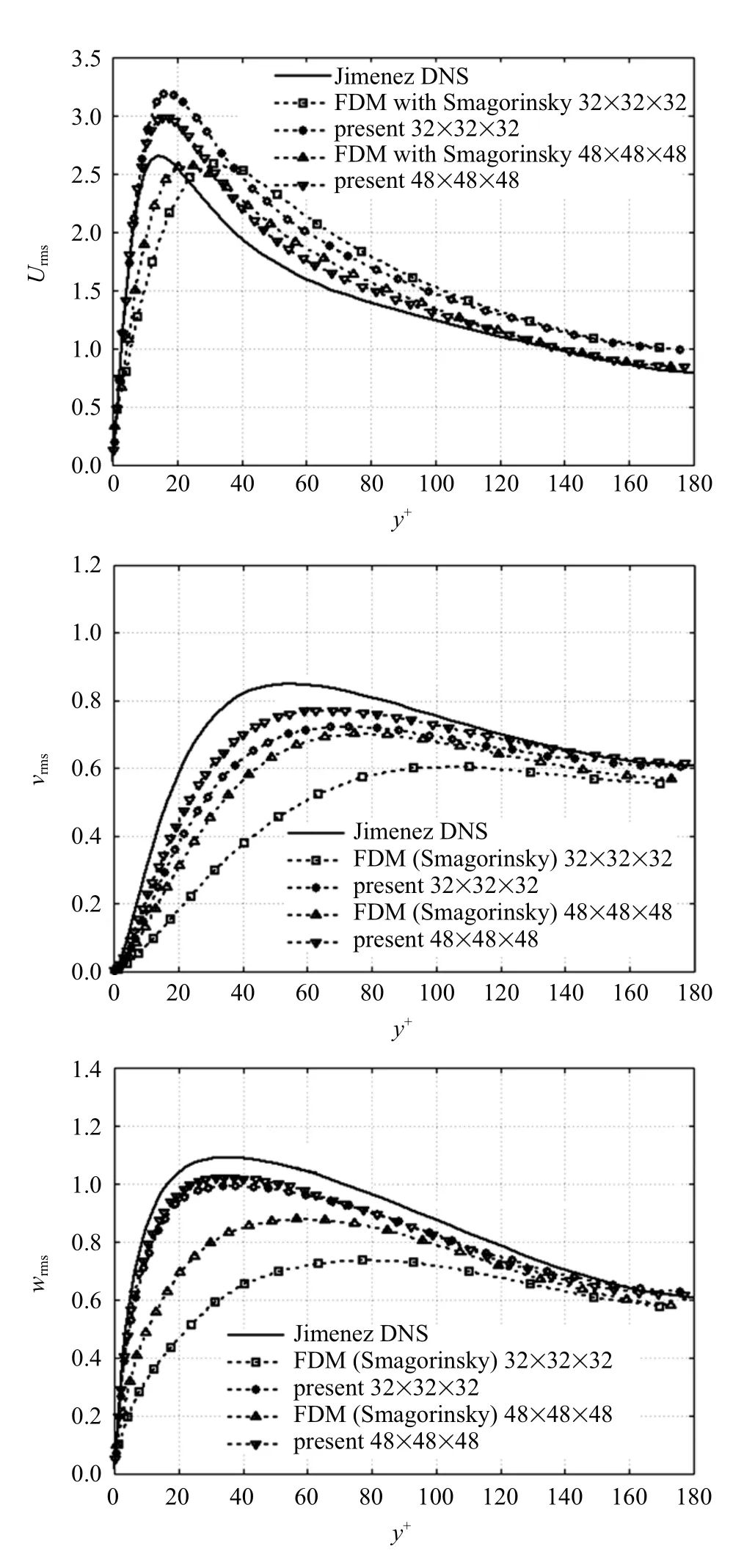
图7 脉动速度均方根值在垂向方向上的分布Fig.7 Root-mean-square of velocity fluctuations against y+

其中u表示任一方向的流场速度,M为xz截面上的空间点数,N为时间采样数.与DNS 结果相比发现本文所用大涡数值模拟的流向脉动速度rms 在壁面附近(y+＜15)DNS 结果匹配良好,然而在对数率区(30 ＜y+＜50)和黏性外层(y+＞50)则略大于DNS的结果; Smagorinsky 模型的计算结果显示流向脉动速度均方根的峰值跟DNS 结果有较大偏差.在垂向与展向上,两种大涡模拟的计算结果均小于DNS 结果; 相比于Smagorinsky 模型的计算结果,本文所得到的结果要更接近DNS 数据.流向脉动速度均方根为湍动能的主要来源,因此它的增加意味着流场整体的湍动能变大,尽管其他两个方向上的脉动速度均方根略有减小,即表明该模型所提供的湍动能耗散略偏小,从而导致图6 中的平均流向速度偏大.

以上结果说明要提高该模型在低网格数条件下的计算精确度,需要改善该模型预测流向脉动速度rms 的能力.另外,根据图7 可以判断,在较少网格情况下使用该模型时,从流向向垂向及展向方向上的湍动能输运略偏低.

图8 为统计平均得到的雷诺应力曲线分布图.如图所示,对于Smagorinsky 模型,由于它提供过大的湍动能耗散,导致各个方向上的速度脉动均减小,因此雷诺应力均减小.与Smagorinsky 模型相比,本文计算得到的雷诺应力略大于Smagorinsky 模型的计算结果,尽管随着网格数的增加,雷诺应力分布有所改进,但结果还是偏小.而雷诺应力值的偏小削弱了流向方向上的湍动能向垂向方向输运.因此,改善该模型对雷诺应力的预测可以有效提高脉动速度均方根的计算精确.

图9 为DNS 数据和48×48×48 网格计算得到的8 ＜U＜10(U为流向速度)的等值面分布图.如图所示,发现DNS 数据得到的等值面图上可以看到很多细小的流场结构,而大涡数值模拟计算得到的流场仅存留了较大尺度的旋涡结构.

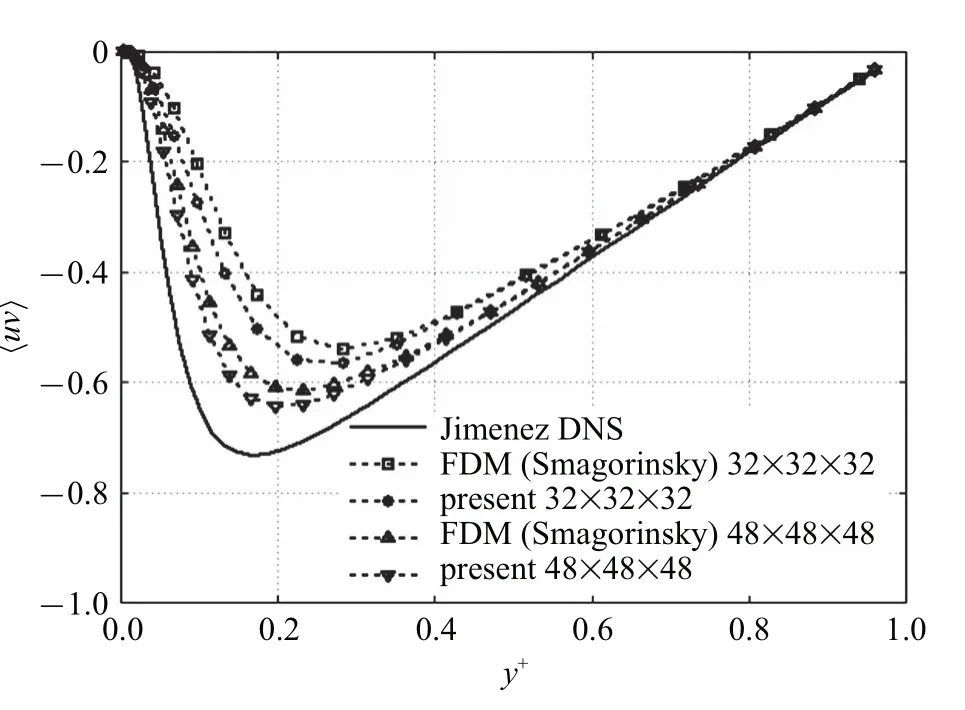
图8 平均雷诺应力项〈uv〉在垂向方向上的分布Fig.8 Reynolds stress against y+

图9 流向速度等值面分布图:(a)DNS;(b)LES(48×48×48)Fig.9 Isosurfaces of streamwise velocity:(a)DNS;(b)present method with 48×48×48 elements

图10 给出了48×48×48 网格计算数据在壁面附近y+=5.4 处xz截面的流向速度云图.从图中可以看出,在近壁面的流场,出现了明显的低速条带结构.近壁面处出现低速条带结构为触发湍流拟序结构的第一号信息.这说明,尽管本文在模拟中使用的网格数较小,该模型还是能有效触发近壁湍流的拟序结构.

图10 近壁面y+=5.4 处xz 截面的流向速度云图Fig.10 Contours of streamwise velocity in the xz plane at y+=5.4

5 结论

本文在有限元的框架下,弓入多尺度的概念,提出了基于多尺度模式的大涡数值模拟方法.论文里采用有限元形函数和权函数空间的分解来实现湍流中大尺度和不可解尺度信息的区分,并推导得到大尺度系统的有限元变分方程.本文通过对不可解尺度系统中各项的特点分析,提出了不可解尺度的近似模式,从而达到封闭大尺度方法的目的.

文中使用新提出的大涡模拟方法的自编程序实现了槽道湍流的并行数值计算.数值计算结果验证了该方法的合理性以及自编程序的收敛性.并得出,该方法可以在使用较少的网格数可以得到与DNS 结果接近的数值解,并在近壁区可以观察到明显的低速条带结构.另外,数值结果证实该方法在网格数较少的情况下流向向另外两个方向的湍动能输运略偏低.