板中热弹波传播:一种改进的勒让德多项式方法1)
2020-11-03王现辉李方琳刘宇建陈会涛禹建功
王现辉 李方琳 刘宇建 陈会涛 禹建功
(河南理工大学机械与动力工程学院,河南焦作 454000)
引言
超声导波检测技术具有高效、低成本的特点,成为无损检测领域快速发展的方向之一[1-3].作为一种有效的导波传播求解方法,勒让德正交多项式方法直接将边界条件通过矩形窗函数弓入控制方程,简化了边界条件的施加方式; 将求解问题的微分方程转化为特征值方程,直接求得表征导波传播和衰减的复特征值,具有精确、高效、适用于处理复杂结构问题等优点.该方法自1999 年提出之后[4],快速应用于各种材料结构,如多层材料[4-5]、圆柱结构[6-8]、梯度材料[9-10]、热弹梯度材料[11]、磁电弹耦合问题[12]、压电材料[13]等.在勒让德正交多项式方法的求解过程中,需要使用勒让德多项式近似位移、温度等物理场变量.同时,为使该方法可解,需要进一步让控制方程推导得到的等式左乘相应的勒让德多项式函数,并对其从结构的一边界向另一边界进行积分.由于该积分核函数中包含有勒让德多项式及其导数,使得该积分的计算时间和计算量均较大.为克服该缺陷,本文基于勒让德多项式的正交性,推导所有积分的解析表达式,降低计算量,减少计算时间,提高计算效率.
随着导波无损检测技术向在线检测方向发展,高温环境下的导波技术受到了越来越多的重视,高温下的热弹耦合问题也成为必须要考虑的问题.一些广义热弹理论,如LS 理论[14],GL 理论[15],GN 理论[16]等被用来处理此类问题.当采用勒让德正交多项式方法求解这类问题时,温度变量需要采用某种形式的勒让德多项式近似表达.对于等热边界条件,仅需在常规勒让德多项式近似的基础上,乘以z(z-h)项即可[11].然而,对于其他边界条件的热弹问题,如绝热边界条件问题,由于缺乏合适的边界条件处理方法,勒让德正交多项式方法无能为力.为进一步扩展该方法的应用范围,本文借助于矩形窗函数,发展一种绝热边界条件处理方法.
LS 理论作为一种有效的广义热弹理论,近年来得到了广泛的发展[17-19].然而,对于很多材料和物理过程,如热黏弹材料和低温过程等,经典的整数阶理论难以有效进行求解[14].幸运的是,分数阶热弹理论[20-23]的发展为这些问题的解决提供了方案.在分数阶理论的基础上,Tiwari 等[24]、Deswal等[25]、Kumar[26-27]对于平面波传播问题进行了研究;许光映等[28]研究了短脉冲激光加热的温度场及热应力场的热物理行为;何天虎等[29]基于非局部效应和记记依赖微分修正的广义热弹性理论,研究了两端固定、受移动热源作用的有限长热弹杆的动态响应.然而就作者所知,分数阶热弹理论目前并未应用于热弹导波传播.在本文中,作者初步将分数阶热弹理论弓入勒让德正交多项式方法,为以后复杂材料或者物理过程的热弹问题有效求解打下基础.
综上所述,本文提出一种改进的勒让德多项式方法,求解分数阶热弹板中的导波传播.推导求解方法中积分的解析表达式,提高计算效率;弓入温度梯度表达式,发展适合勒让德多项式级数的绝热边界条件处理方法.与已有文献结果对比表明改进方法的正确性;与已有方法的CPU 计算时间对比说明改进方法的高效性.最后将改进的方法用于求解分数阶热弹板中的导波传播,研究分数阶次对频散、衰减曲线和应力、位移、温度分布等的影响.
1 改进的勒让德多项式法
1.1 分数阶热弹板导波传播问题求解
基于分数阶LS 热弹理论,热弹导波传播问题的控制方程可以如下表达

应变和位移关系,以及本构方程表达式如下
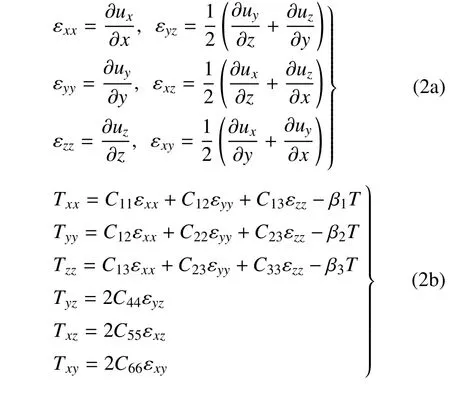
其中,u是位移,T是温度,Tij为应力,εij是应变,Kj是材料常数,βi为热胀系数,T0=296 K,Ce为特定常数,ρ 是密度,Cij是弹性系数,α 是分数阶次,τ0是松弛时间.
为求解该问题,必须进行无量纲化[30]


进一步,假设板内为x+方向传播的自由谐波,则位移和温度的表达式可设为

其中,k为波数,ω 是角频率.在此基础上,将式(2)~式(5)代入式(1),简化推导过程,并重写为,控制方程(1)由可转化为下面的方程组


在式(6) 中,·′和·′′表示对z的一阶和二阶导数.为求解方程组(6),可将位移、温度等物理场变量进行勒让德多项式近似

式中,Pm,分别是勒让德多项式及其展开系数,h为板的厚度.在等温边界条件中,温度表达式可表达如下[11]
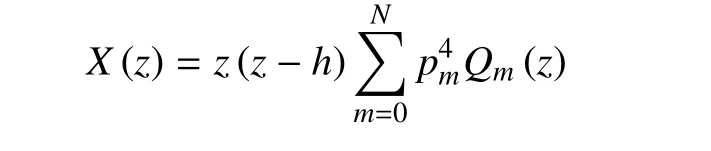
不同于等温边界条件,绝热边界条件无法通过一个展开公式进行表达,需再假设温度梯度的表达式如下
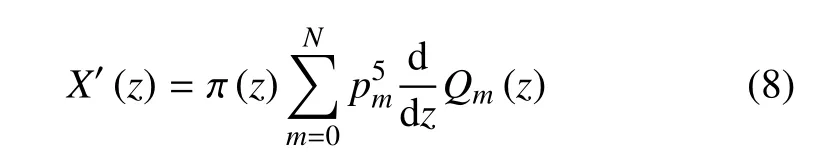
将式(7)中的温度表达式X(z)对z向求导,其结果必然要等于式(8)中的温度梯度表达式,然后让该等式两边同乘以Qj(z),j=0,1,...,N,并进行积分,则可以得到方程组Hp5=Hp4.易知,p5=p4.
通过温度及其梯度的表达式,可扩展勒让德多项式法求解绝热边界条件下的热弹问题.
将式(7)和式(8)弓入方程(6),方程可转为下面的矩阵形式

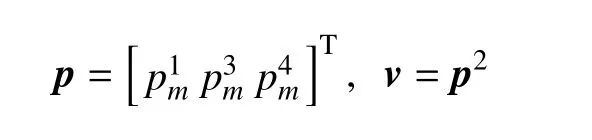
Ai j,Bi j,Cij,Mij,D,E是将方程(7)和(8)代入式(6),并进行积分后形成的矩阵.方程(9a)由方程(6a),(6c) 和(6d) 得到,方程(9b) 由独立方程(6b) 推导求得.
然而,方程(9) 并不具备一般特征值结构形式.本文弓入波数相关特征向量,进行矩阵变换得到特征值结构形式的方程组.设向量q=kp,方程(9)可转化为如下特征方程

通过特征值方程组(10),分数阶热弹导波问题的特征值和特征向量即可快速得到.
1.2 解析积分
在程序运行过程中,积分所消耗的时间占总CPU 计算时间的比例可高达97%以上(见表2),因此有必要通过有效的方法,降低积分计算量,减少积分时间,提高计算效率.积分解析化是实现该目标的一种有效手段.本节基于勒让德多项式的正交性,对程序运行过程中的所有积分进行解析表达.通过分析,所有积分可归纳为以下5 种积分

h(t)为Heaviside 函数.在这5 种积分中,I1,I4和I5可直接得到
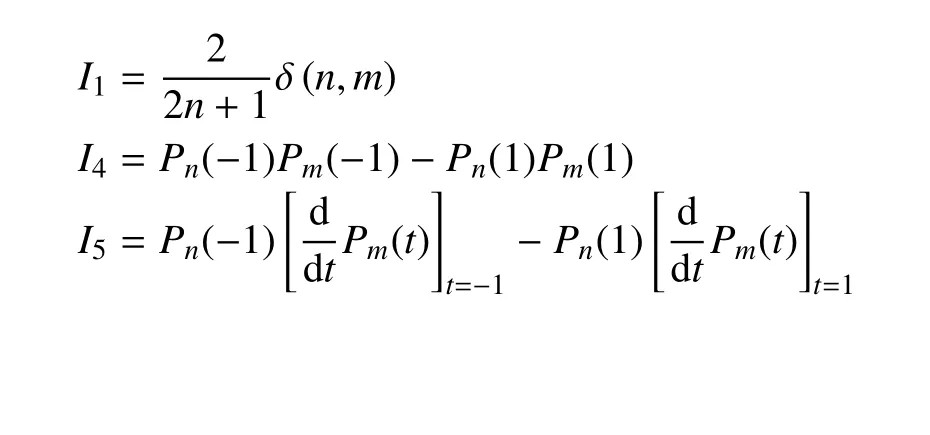
为求解I2和I3,参考文献[31],推导勒让德多项式导数的展开式,简化推导过程,其结果是

基于这两个表达式,当m>n,mod(m-n,2)=1,l=(m-n-1)/2,I2=2(2m-4l-1)/(2n+1),其他I2=0.当m>n+1,mod(m-n,2)=0,p=(m-n-2)/2,I3=2(m-4p-3)(p+1)(2m-2p-1)/(2n+1),其他I3=0.
基于这5 个解析积分表达式,可降低算法的计算量,有效减少计算时间,提高计算效率.
2 数值算例
本节将提供3 个算例,第一个算例验证算法和程序的有效性,第二个算例表明改进算法的计算效率,第三个算例研究分数阶次的影响.本节中,板的材料性质和文献[30] 一致,C11,C13,C33,C44,C55分别为5.74×1011,1.27×1011,4.33×1011,1.19×1011,1.08×1011N/m2,P为3.2×103kg/m3,Ce为670 J·kg·(°)/m,β1和β3分别为3.22×106和2.71×106N/((°)·m2),k1和k2分别为55.4 和43.5 W/(m·K).本文数值实验所使用软件为Mathematica,电脑配置CPU:Inter core I7-4790,3.6GHz;内存:16G.
2.1 改进算法的有效性
由于缺乏分数阶热弹板中导波传播的研究成果,本文将和整数阶(α=1)的热弹导波频散曲线[30]进行了对比,如图1 所示.结果显示由改进的勒让德多项式法得到的频散曲线和已有结果完全一致,表明本文的算法和程序是正确有效的.
2.2 改进算法的高效性
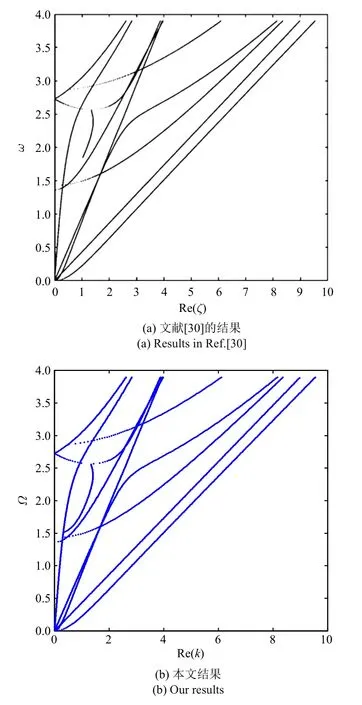
图1 和已有结果对比Fig.1 Comparing with the existed result

表1 390 频率计算点的CPU 计算时间(CLPA)Table 1 CPU time with 390 frequencies(CLPA)
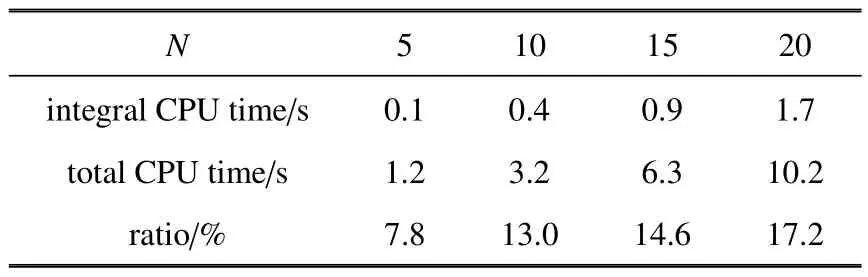
表2 390 频率计算点的CPU 计算时间(AILPA)Table 2 CPU time with 390 frequencies(AILPA)
在本节中,通过对不同展开阶次勒让德多项式的CPU 计算时间进行统计,研究改进方法的计算效率.传统勒让德正交多项式方法(conventional Legendre polynomial approach,CLPA)和本文改进的勒让德正交多项式方法(analytical integration Legendre polynomial approach,AILPA) CPU 计算时间(s)分别如表1 和表2 所示.表1 结果表明,已有方法积分时间占总计算时间的比重最高为97.8%,这意味着几乎程序所有的计算时间都用来进行积分.表2 结果表明积分时间占总CPU 计算时间的比重最高为17.2%,这意味着仅有不足1/5 的计算时间都用来进行积分.表1 和表2 的数据对比表明改进方法计算积分的时间大大减少,致使总体CPU 计算时间大幅度降低.图2 为AILPA 的总计算时间占CLPA 的总计算时间的百分比,从图上可知,当N=5 时,占比最高,此时为21.05%,并且随着展开阶N的增大,该占比不断下降.值得注意的是,在N=20 时,AILPA 的总计算时间仅为10.2 s,为CLPA 总计算时间(392.4 s) 的2.6%.因此,和CLPA 相比,改进算法的计算效率得到极大提高.
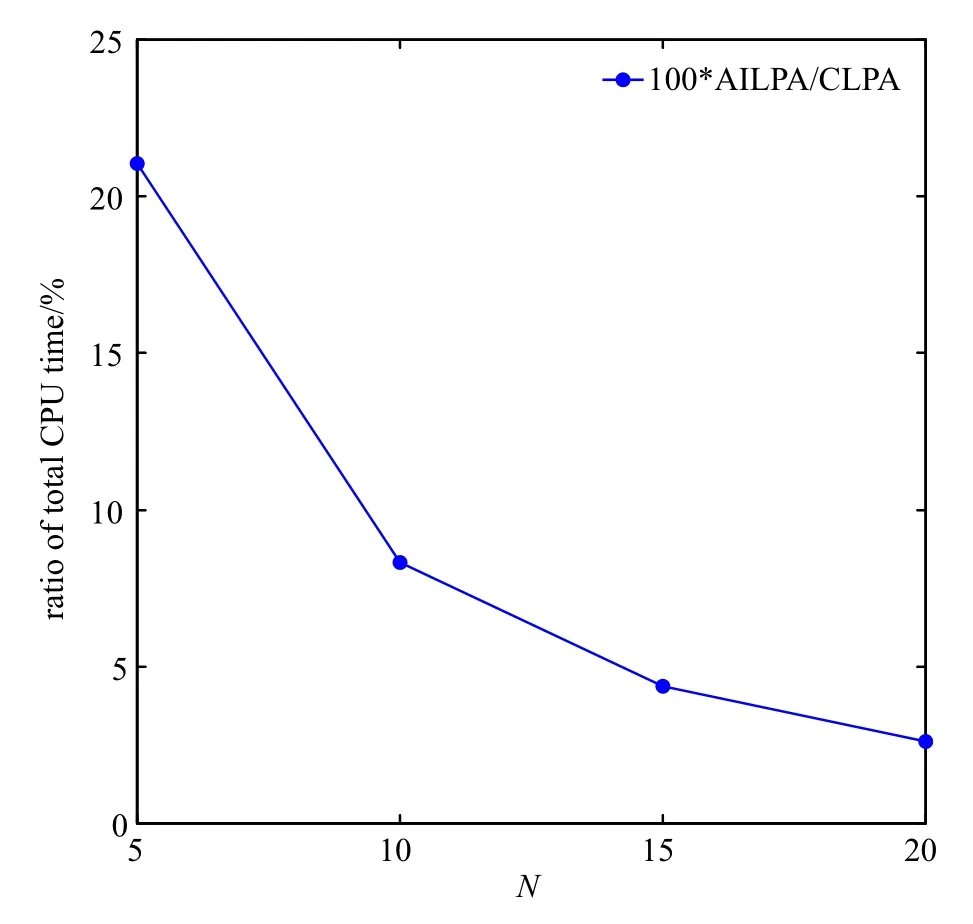
图2 两种方法CPU 总时间的比值Fig.2 Ratio of two total CPU time
2.3 分数阶的影响
在本节中,将通过对不同分数阶次的频散曲线和应力、位移、温度分布进行对比,研究分数阶次的影响,松弛时间τ0=1.440×10-13s (无量纲t0=1).图3 为不同分数阶次时的相速度曲线,从图中可知,热波波速大于弹波波速.另外,大部分的相速度曲线(弹波相速度)在不同的分数阶次下几乎完全相同,这表明弹波传播受分数阶次的影响较小,这主要因为在热弹控制方程中,热弹耦合系数较小,仅为0.002 49,因此温度对弹波的影响也非常小.同时,图3 标注的热波曲线随着分数阶有一定的变化,这表明热波传播受分数阶的影响较大.但是两个热波相速度在分数阶的影响下,变化趋势并不相同.对于无截止频率的热波,分数阶α 越小,其相速度越大.而对于另一热波,当频率较小时,分数阶α 越大,相速度越大;当频率较大时,分数阶α 越大,相速度越小.

图3 不同分数阶次的相速度曲线Fig.3 Phase velocity comparison of different fractional order
由于弹性模态更适合于进行无损检测,因此需进一步研究分数阶次对弹波衰减的影响.图4 为不同分数阶次时弹波波数的虚部值对比.结果显示,随着分数阶次的变化,弹波波数的虚部值也随着变化.其中模态2 和3 受分数阶的影响较大,且具有相同的趋势,即分数阶α 越大,波数虚部值越大.这意味较大的分数阶α 值,在部分弹波模态传播时具有较大的衰减速度.因此,在使用弹波进行无损检测时,分数阶对衰减的影响不可忽略.
图5~图7 分别给出了位移(uj)、应力(Tij) 和温度(T)及温度梯度(Tz)分布的情况,其中—–表示α=0.2,–·–·–表示α=0.5,--------表示α=0.8.从3幅图上可知,(1)分数阶α 影响位移、应力和温度的分布; (2) 分数阶α 影响所有模态的温度分布,但仅有热波的位移和应力受到分数阶α 的影响较大;(3)z向应力和温度梯度分布曲线均是从0 到0,这进一步表明了程序的正确性.另外,温度梯度分布曲线从0到0 说明绝热边界条件处理方法的正确性.

图4 不同分数阶的弹波虚部波数对比Fig.4 Comparison of imaginary part wave number of elastic wave with different fractional order
3 结论
针对勒让德正交多项式方法求解热弹导波传播时存在的两个不足之处,本文提出一种改进的勒让德正交多项式方法,以求解分数阶热弹板中的导波传播.本文主要创新点是:(1) 采用解析积分代替原有的数值积分,极大提高了算法的计算效率.该积分表达式可推广至压电材料、圆柱等均匀结构; (2)发展一种适用于勒让德多项式级数的绝热边界条件处理方法,扩展了原有算法的求解范围;(3)将改进的方法应用于分数阶热弹板,研究分数阶次对频散、衰减曲线和位移、应力、温度分布等的影响.主要研究结论如下.
(1)分数阶α 对热波相速度具有较大的影响,但对弹波的相速度影响较小.然而,分数阶对弹波衰减具有一定的影响;
(2)分数阶α 影响所有模态的温度分布,但仅热波的位移和应力受分数阶α 的影响较大.
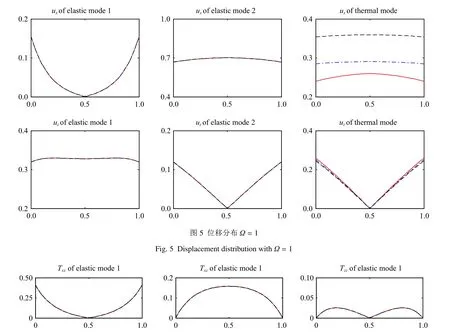
图6 应力分布Ω=1Fig.6 Stress distribution with Ω=1
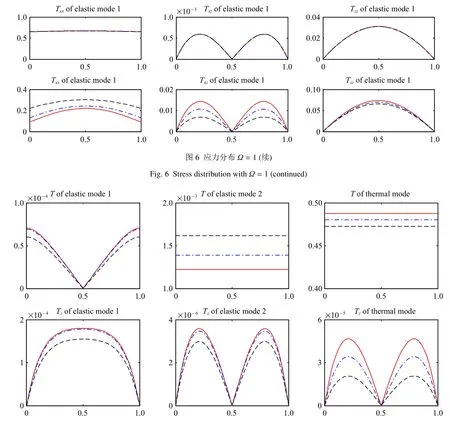
图7 温度及其梯度分布Ω=1Fig.7 Temperature and its gradient distribution with Ω=1
