建房切坡条件下边坡稳定性分析

杜显祥，房 浩，曹佳文

(1.天津市地质环境监测总站，天津 300191;2.中国地质环境监测院，北京 100081；3.北京师范大学水科学研究院，北京 100875；4.中国地质调查局，北京 100037)

0 引言

边坡是工程建设活动及人类生存中常见的自然地质环境之一，边坡岩土体失稳后产生的崩塌、滑坡等地质灾害将会给人民的生命财产安全带来难以想象的损失[1-2]。然而随着我国城乡建设的不断发展，农村山区私人建房过程中通过开挖坡体增大建筑面积的现象逐渐增多，切坡建房后形成的高陡人工边坡给崩塌滑坡等地质灾害的发生埋下了隐患。浙江是全国地质灾害多发省份之一，据调查统计全省由切坡建房引发的地质灾害占60%～80%[3]，以经济较为发达的余杭区鸬鸟镇为例，区域内由切坡建房引发的地质灾害占56.4%、产生的不稳定斜坡占总数的95.5%[4]。

为降低边坡工程建设引发地质灾害的可能性，合理开发利用土地资源，国内外许多学者在边坡开挖与其稳定性方面做出了很多研究。

国际著名边坡分析专家DUNCAN[5]于1996年对20世纪70、80年代出现的各种极限平衡法如瑞典圆弧法[6]、Bishop法[7]、Janbu法[8]、变分法[9]等进行了总结。虽然以上方法都可大致探索到边坡潜在滑动面的位置规律，但由于没有考虑边坡实际开挖工况下岩土体本身的应力-应变关系，所求得到的应力应变关系不能代表实际工作状态下的应力应变，也不能求得边坡开挖后实际的变形数据。随着计算机技术的快速发展，数值分析法被逐渐推广使用到边坡稳定性分析中来，如有限元、有限差分等方法，以及后续的极限平衡与数值分析相结合的方法[10]。就此AYBE RK KAYA[11]结合运动学、极限平衡和数值稳定性分析三种方法，对玄武岩、凝灰岩中的隧道入口挖掘之后对附近边坡上的房屋破坏机理进行了研究，研究表明边坡失稳与岩体扰动后岩体和节理的强度降低有关。SARI,M.[12]提出了关于岩体的Hoek-Brown破坏准则和节理的Barton-Bandis抗剪强度准则，并结合极限平衡法与数值分析法获得边坡滑动破坏模式，其能够增加边坡开挖后稳定性评估的准确性。

国内相关领域的学者也开始了有关边坡开挖及其稳定性方面研究。宋子岭等[13]基于刚体极限平衡法和强度折减法，应用GEO-SLOP、ANSYS及FLAC3D软件对多层软弱顺层边坡稳定性进行研究，得出边坡潜在的滑坡模式，同时指出结合多种计算模拟方法，对比研究可提高边坡稳定性分析结果的可靠性。陈晓利等[14]利用二维极限平衡数值模拟方法，分析了边坡开挖位置对边坡稳定性的影响，给出了在保证边坡稳定性的前提下不同坡体所适宜的开挖位置。吴军等[15]通过MADIS GTS建立边坡数值模型，研究不同开挖深度边坡的应力分布特征及坡顶建筑物位移特征，揭示了边坡—坡顶建筑物失稳机理。穆成林等[16]以边坡岩体结构类型为基础，采用未确知测度理论对开挖边坡进行稳定性预测评价，建立了“岩体结构-指标组合赋权-未确知测度理论 ”的新评价体系,结果表明预测结果与实际具有较好的一致性，对相关工程领域具有借鉴作用。

然而，以上研究都未从灾体本身特征与致灾因子之间的综合关系来分析不同边坡开挖工况下对边坡的稳定性影响，也未从定量的角度给出边坡工程开挖建设方案。

为此本文以浙江省余杭区鸬鸟镇为研究区，选取研究区内具有不同坡度的斜坡建立二维数值模型。借助Geo-studio软件，结合有限元法与极限平衡法模拟斜坡在不同进尺开挖工况下的应力应变重分布及稳定性规律，寻找边坡安全系数与开挖进尺之间的函数关系，反演推算边坡失稳状态下的开挖工况，以期给研究区内切坡建房工程活动提供切实可行的边坡开挖施工方案，有效降低切坡建房引发地质灾害的可能性，使山区村民生命财产安全得到保障。

1 基于有限元极限平衡法的边坡稳定性分析原理

目前边坡稳定性定量分析方法有建立在刚体极限平衡理论上的极限平衡法与以有限元为代表的数值计算方法两类[17-18]，但两者在运用中各自存在一些问题。极限平衡法视边坡岩土体为刚体，虽能给出物理意义明确的边坡稳定性系数以及可能的破坏面，但此方法未能考虑岩土体本身的应力应变关系，不能很好地反应边坡的破坏机理。有限元法则将边坡岩土体看成是变形体，能够有效克服刚体极限平衡法的缺陷，进行土体应力应变之间非线性关系的模拟计算，确定边坡应力分布特征，大致确定滑动面位置。考虑到人工切坡建房后，边坡的应力应变分布状况发生改变，岩土体不能单纯的视为刚体来模拟计算安全系数，因此既要考虑岩土体应力应变关系又要得到确定的边坡安全系数，则需要结合极限平衡法与有限元法的优点，耦合两者基本模型进行边坡稳定性分析及安全系数计算[19]。

有限元极限平衡法是基于有限元计算得到的应力场作为极限平衡分析时搜索边坡潜在滑移面的实际应力，将边坡进行条分获得条块计算参数，计算条块底面中心点坐标应力，根据安全系数定义，通过有限元法与极限平衡法的耦合进而求解安全系数[20]。

将边坡体简化为二维问题，按传统边坡安全系数定义，平面应力状态下，根据滑面上任一点应用摩尔—库伦强度准则，滑动面安全系数FS定义为沿滑动面土体抗剪强度与实际剪应力的比值[21]:

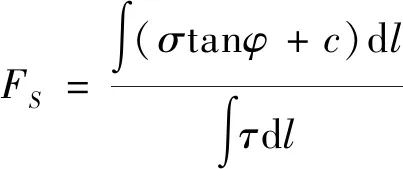
(1)

式中：c、φ——土体的抗剪强度指标，凝聚力和内摩擦角；

σ、τ——有限元计算条块单元体上法向应力与剪切应力；

l——潜在滑体的总长度。通过弹塑性有限元分析，计算出对于每个单元高斯积分点的σx、σy、τxy，进而利用差值函数求出各土条中点的σx、σy、τxy，用摩尔圆来计算土条底部的正应力和剪切力，按照上述公式计算FS值，重复上述处理直到第n个土条。

2 研究区地质灾害概况与边坡模型构建

2.1 研究区地质灾害概况

余杭区鸬鸟镇地处山地丘陵区，社会经济较发达，同时也是地质灾害相对较频发的地区。根据以往地质灾害调查数据统计结果显示，区内地质灾害多发生在坡度为15°～35°的斜坡内，占有地质灾害斜坡总数的75%以上[22](图1)。分析统计已发生的地质灾害在不同工程地质岩组内的分布，其中近54%的地质灾害分布在以花岗岩为主的酸性岩岩组范围内(图2)，因其全风化层厚度大，在 5～15 m之间，且结构较松散，上覆有薄层的第四纪残坡积层，因此较易发生地质灾害。为全面了解地质灾害发育状况，2018年6月至10月项目组对研究区所有地质灾害点进行野外实地踏勘，调研地质灾害点的诱发因素，统计分析地质灾害点分布与人类工程建设活动之间的关系。研究结果表明大部分地质灾害是由于建房、修路及采矿等人类工程活动中产生高陡边坡所引起，且施工过程中基本是以90°角垂直地面对斜坡进行开挖，其统计结果如表1所示。

图1 地质灾害坡度统计分布图Fig.1 Statistical distribution map of the slope of geological disaster

图2 地质灾害在不同工程地质岩组中的分布图Fig.2 Distribution of geological disasters in different engineering geological rock groups

表1 地质灾害与人类工程活动关系统计表Table 1 Statistical of relationship between geological hazards and human engineering activities

2.2 边坡模型构建

为全面反映研究区地质灾害发育分布规律，结合上述对研究区地质灾害与斜坡、工程地质岩组及人类工程活动之间的分布特征统计分析结果，选取地质灾害多发的坡度为10°、20°、30°和40°的斜坡为对象构建边坡的物理力学模型，具体建模过程如下。

(1)模型区域设定：为控制单一变量，选择地质灾害发生的主控剖面为模型面域，设定斜坡高度20 m不变，通过改变坡脚距坡顶的水平距离来构建斜坡模型，再通过改变坡脚处不同开挖进尺来实现不同开挖工况。

(2)本构模型确定：根据钻孔揭露的岩层垂直分布情况，将坡体概化为由残坡积层与全风化花岗岩(中砂)两层均质材料组成的莫尔—库仑模型。

(3)边界条件设置：研究区边坡发生滑动属于局部小规模的滑动，故将模型的纵坐标方向设定无水平位移，横坐标方向设定无竖向位移(图3)。

(4)区域网格剖分：网格划分的大小与计算目标的匹配程度、网格质量的好坏是有限分析结果成败的重要控制因素。对边坡模型进行有限元区域网格划分时，为保证有限元求解精度、准确性及计算速度，设定格点间距大小为1 m，在两种材料的过渡区利用四边形和三角形单元进行衔接，将模型各区域划分为多个独立单元格。

(5)材料参数赋值：根据工程钻探及土工试验结果，赋予模型材料的物理力学参数如表2所示。

表2 模型计算所需物理力学参数Table 2 Physical mechanical parametersof model calculation

通过以上建模步骤，得到具体的物理模型如图3所示，本文仅以30°斜坡为例展示。

图3 30°斜坡二维物理模型Fig.3 Two-dimensional physical model of the slope with a slope of 30°

3 不同开挖工况下边坡稳定性模拟计算

模拟计算采用Geo-studio软件，该软件是加拿大GEO-SLOPE公司开发的一套岩土工程仿真分析软件，它包含边坡稳定性分析模块Slope/W与岩土应力应变分析模块Sigma/W等一系列分析计算模块，其模块之间可以相互结合达到综合分析的效果。如果单纯的基于Slope/W模块采用极限平衡法求解边坡安全系数，其求解得到的结果虽能给出确定的安全系数值，但却是假定滑裂面上的平均安全系数，并没有考虑土体本身应力应变关系下边坡失稳的破坏机理。因此本文首先基于Sigma/W模块利用有限元法分析不同开挖工况下边坡的应力应变重分布情况，然后将分析结果导入到Slope/W模块中，结合极限平衡法求得平衡状态下的安全系数及其潜在失稳区的分布情况，从而实现有限元法与极限平衡法相结合进行边坡稳定性分析及安全系数计算。

计算过程中采用莫尔-库仑理想弹塑性模型，首先对未开挖状态下坡体进行模拟计算，之后从坡脚开挖，开挖进尺从2 m到10 m，每开挖2 m记录一次坡脚处的剪应力分布规律，并计算开挖后坡体的安全系数。分别模拟计算得到四种斜坡不同开挖工况下的安全系数如表3所示、开挖卸荷后坡脚处的剪应力如表4所示。

表3 四类斜坡不同开挖工况下安全系数统计表Table 3 Statistical table of safety factors under different excavation conditions

表4 四类斜坡不同开挖工况下坡脚剪应力/kPa统计表Table 4 Statistics table of the Slope shear stress (kPa) for different excavation conditions of four types of slopes

4 人工开挖对斜坡稳定性影响规律研究

4.1 开挖后边坡应力应变重分布规律研究

为了便于分析边坡开挖后坡脚附近的变形破坏情况，单独选取角度为30°的斜坡，分析斜坡未开挖状态下应力应变分布规律，同时提取斜坡开挖进尺为10 m时竖向距离5 m处(截面aa)、6 m处(截面bb)、7 m处(截面cc)、8 m处(截面dd)、9 m处(截面ee)、10 m处(截面ff)截面上各点的水平方向的应力与应变值做对比分析，各截面位置示意图如图3所示。

由图4分析可得，30°斜坡在未开挖状态下，斜坡坡顶的应力大于坡脚处，并且其最大应变值出现在坡顶区域，因此可推测在斜坡未开挖时其潜在失稳区域为坡顶。随着边坡开挖进尺的加大，坡脚卸荷，水平应力骤升，使得坡脚处的应变值大于坡顶处。为推测出开挖后具体的变形破坏位置，绘制了各截面水平应力应变曲线图(图5)，30°斜坡开挖10 m时，除aa截面的水平应力在坡脚附近有较大幅度的上升，其余截面水平应力值均呈下降趋势，并且下降至低于未开挖状态时的应力，表明开挖后坡脚以上5 m范围内其稳定性有所提高。再由各截面水平应变值曲线图分析可得，ee、ff截面的水平应变基本为负值，bb、cc、dd截面则由负值变为正值再变为负，出现明显的峰值，aa截面在坡脚处水平应变值骤升，且超过坡顶处的应变值，表明开挖后边坡坡顶和坡脚都成为潜在的失稳区，并且坡脚处的应变值大于坡顶处，此时边坡最可能的失稳区为坡脚附近2 m范围内。

图4 30°斜坡未开挖时边坡主控剖面上水平应力与应变分布图Fig.4 Horizontal stress and strain distribution on the main section of the slopewith the slope is 30°

图5 30°斜坡开挖10 m时边坡典型坡面上水平应力与应变分布图及各截面曲线图Fig.5 Horizontal stress and strain distribution and cross-section curvesat the main section of the slope with a slop is 30°while the excavation depth is 10 m

4.2 开挖后边坡安全系数变化规律研究

边坡开挖后，坡脚处形成具有一定高度的临空面，改变了边坡的应力分布状态。由不同开挖工况下坡脚剪应力统计表4可以看出，坡脚处的剪应力在开挖卸荷后具有不同程度的增大，并且坡度越大开挖后的剪切应力增幅越大。同时统计分析开挖后边坡安全系数的变化趋势，得知自然坡度越大的斜坡，开挖一定进尺后安全系数下降的幅度越大，坡度为10°的斜坡开挖10 m后安全系数降幅为20%，坡度为40°的降幅为39%。

为探究不同开挖进尺工况与边坡安全系数之间的关系，针对四类不同角度的斜坡利用spss软件模拟构建开挖进尺与安全系数的函数关系曲线，并得到具体的函数表达式(图6)。表达式中Y为不同开挖进尺下的安全系数，x为开挖进尺。

图6 四类斜坡不同开挖进尺工况与边坡安全系数函数关系图Fig.6 Relationship between different working conditions of four types slopes and safety factor

以上由函数关系曲线分析可得，自然坡度10°斜坡开挖后安全系数变化较平稳，其他三类斜坡在开挖后安全系数下降迅速。以自然坡度40°斜坡为例，开挖过程中边坡卸荷集中，坡脚剪切应力骤升，当开挖进尺至4 m时安全系数降至为0.986，边坡处于失稳状态。通过所建立的函数关系曲线，推算出每类斜坡在边坡失稳临界状态下，安全系数为“1”时的开挖进尺分别为29.6 m、13.2 m、10.1 m、2.5 m。为验证推算得到的开挖进尺临界值的可靠性，重新构建以上开挖进尺边坡模型，模拟计算得到安全系数分别为3.348、1.088、1.011、0.989，其模拟结果显示对于坡度较小的斜坡，利用以上模拟函数推算不同开挖进尺下的安全系数误差较大，而对于坡度较大的斜坡则误差为10%左右，误差较小，其函数关系可为切坡建房工程活动提供可靠的施工方案，有效降低因切坡建房引发地质灾害的可能性。

5 结论

本文通过调查分析研究区内地质灾害与边坡分布特征，构建四种具有不同坡度的自然斜坡二维模型，利用有限元极限平衡法模拟斜坡开挖与不开挖状态下边坡应力应变重分布规律及不同开挖工况下边坡稳定性规律，得出以下几点结论：

(1)基于有限元极限平衡法模拟边坡稳定性，既可以得到可靠的安全系数，又能够得到开挖后边坡的应力应变分布规律。未开挖状态下，坡顶处的水平应变大于坡脚处，斜坡潜在的失稳区域位于坡顶处；开挖后，边坡应力重分布，坡脚处水平应力应变骤升，且数值大于坡顶，致使坡顶和坡脚都成为潜在的失稳区。

(2)在人工切坡工程活动中，影响边坡稳定性因素有边坡自然状态下的坡度与边坡开挖进尺两种。斜坡坡度相同，开挖进尺越大，边坡安全系数越小，并随着开挖进尺增大，安全系数降低速率越快；开挖进尺相同，坡度越大的斜坡对开挖工程活动越敏感，坡度为10°的斜坡开挖10 m后安全系数降幅为20%，坡度为40°的降幅为39%。

(3)通过拟合边坡开挖进尺与开挖后安全系数之间的函数关系，可推算得到各类边坡失稳时的开挖进尺临界值，利用开挖进尺临界值模拟计算边坡失稳临界状态时的安全系数与“1”进行误差分析，结果显示坡度小于20°的斜坡误差大，坡度大于20°的斜坡误差小，为10%左右。其拟合的函数关系可预测边坡开挖后的安全系数，为切坡建房工程活动提供合理的边坡开挖方案，有效降低切坡建房工程活动过程中地质灾害的发生。