基于BA-LSSVM模型的黄土滑坡致灾范围预测

吴 博，赵法锁，贺子光，段 钊，吴韶艳

(1.长安大学地质工程与测绘学院，陕西 西安 710054；2.黄淮学院建筑工程学院，河南 驻马店 463000；3.西安科技大学地质与环境学院，陕西 西安 710054)

0 引言

长期以来，滑坡的致灾范围预测一直是国内外学者关注的重点和难点，研究内容主要包括滑坡的纵向滑动距离(L)和横向扩展距离(W)两个基本量化指标。对于纵向滑动距离研究成果较多，归结起来主要包括统计回归法、理论计算和数值模拟三种办法。统计回归法就是根据已有的滑坡资料，将各影响滑动距离的因素进行相关性分析及回归拟合，建立滑距预测公式[1-4]；理论计算是根据能量守恒定律、质点运动等原理，对部分滑动条件进行假设，通过公示推导出滑距的计算公式[5-8]；数值模拟方法主要是基于准确的滑坡地形、地层结构特征，通过试验方法获得岩土体的物理力学参数，采用连续介质或非连续介质等数值模拟方法，对滑坡滑距进行计算分析[9-11]。而对于横向扩展距离研究成果较少，工程上经常采用选取滑源宽度以15°的扩散角扩展进行预测[3]，但未得到理论证明；亓星等[12]对黑方台静态液化型滑坡统计研究发现，此类滑坡横向堆积距离与滑源区最大宽度呈正线性相关关系。近年来，部分学者结合非线性现代数学理论提出了一些新的滑坡滑距预测的研究方法，如李骅锦建立了基于BP神经网络模型，通过分析滑距与滑坡体积参数、地形地貌参数之间的关系，为滑坡滑距预测提供一定的依据[13]；王鼐选取地震烈度和坡度因子，建立基于模糊信息优化处理的预测模型[14]。

近些年来，人工智能方法得到了迅速的发展，其中由于支持向量机能够解决样本少、易陷入局部最优等问题，具有很强的泛化能力，在各个领域都有应用。最小二乘支持向量机是在继承了支持向量机的优点的基础上，采用最小二乘线性系统作为损失函数，加快了求解速度，但同时其性能也过于依赖训练参数，参数的优劣直接决定了模型的准确度。参数的寻优便成为了最小二乘支持向量机的重点。目前学者们通过智能优化算法对模型参数进行寻优，例如模拟退火算法、粒子群算法、遗传算法等，其中蝙蝠算法(BAT Algorithm,BA)是一种基于模拟蝙蝠觅食行为的启发式智能算法[15]，能够解决在寻优中陷入局部最优的问题，已经应用到分类、设计、边坡稳定性等多个领域，在准确性和有效性上有着明显的优势。

为最大程度的保障人民生命财产安全，有效进行防灾减灾，本文以陕西泾阳南塬滑坡为研究对象，选取滑坡基本特征参数为样本数据，建立基于蝙蝠优化算法的最小二乘支持向量机的预测模型，对泾阳南塬滑坡的致灾范围进行预测，为该地区的滑坡威胁范围确定和危险评估提供参考。

1 泾阳南塬滑坡概况

泾阳南塬位于陕西省泾阳县南部，是渭北黄土台塬的一部分，地势平坦，黄土厚度覆盖较厚，由于受到渭北台塬斜揭式隆起和泾河侧蚀的作用，使得泾河南岸阶地不断缺失，在塬边形成高陡边坡，高差约30～130 m，形态陡直，呈“L”型，坡脚为平坦的泾河Ⅰ级阶地，坡脚一般无支撑，为滑坡的发育提供了良好的地形地貌条件；塬边的地层主要由Q2黄土组成，其间夹有若干层古土壤，性质差异较大，在受到人工引水灌溉和降雨作用，地下水位不断抬升而逐渐形成软弱面。因此，研究区内的滑坡都有“灌溉背景”。

因此，本文主要针对由于人工灌溉诱发的黄土塬边滑坡，由于研究区内的滑坡所处的地形地貌(“L”型边坡)、地层结构(黄土)、形成机理(地下水位抬升、土体强度降低)、诱发条件(人工灌溉)均基本相同，故在选择指标时不再考虑这些影响因素，而以滑坡形态特征参数(滑坡体积、滑坡高度H(前缘到剪出口的垂直距离)、滑源区水平长度Ls、滑源区水平宽度Ws)作为致灾范围的影响因子，本文基于现场调查、遥感解译等获取了其中59个滑坡形态特征参数(部分数据见表1，数据统计见图1、2)。

表1 部分滑坡特征数据表Table 1 Data of partial landslides characteristics

图1 影响因素特征数据示意图Fig.1 Schematic diagram of characteristic data of influencing factor

图2 滑坡31数据示意图Fig.2 Schematic diagram of data of No.31 landslide

2 最小二乘支持向量机基本理论

最小二乘支持向量机是支持向量机的一种改进方法，通过引入平方项的方法，使其目标函数的约束从不等式变为等式，将二次规划问题转化为线性方程组进行求解，极大提高了计算精度和速度，得到了更强的泛化能力。

将{(xi,yi)|xi∈Rn,yi∈R,i=1,2,3,…,n}向量集作为学习样本，其中xi为n维输入数据向量，yi为一维输出向量，利用φ(x)将原始样本映射到特征空间中，构造最优决策函数：

y=ωTφ(x)+b

(1)

式中：ω——权值向量；

b——修正系数。

根据结构风险最小化原则，引入松弛变量ei，寻找ω和b使得y最小值，可得到如下最小二乘支持向量机模型：

(2)

约束条件为：

yi=ωTφ(x)+b+ei,i=1,2,…,n

(3)

其中：γ——正则化参数或者惩罚因子，用于控制大偏差样本个数以及回归参数的平坦度。

为了求解该优化问题，引入Lagrange函数：

(4)

对式(4)进行偏导数计算，得：

(5)

整理式(5)，可得如下n+1维方程组：

(6)

(7)

式中的αi和b可以由式(5)解得，本文选取径向基函数(Radial basis function)作为核函数，其表达式为：

(8)

式中：xi——输入向量；

xj——第j个径向基函数中心；

σ2——核函数的形状参数。

综上，在最小二乘支持向量机中，只要能够获得式(2)中的正则化参数γ和式(8)中的核函数形状参数σ2，即可得到最优解。鉴于蝙蝠算法相比较其他算法具有局部搜索能力强、计算收敛速度快等特点，本文选择BA对正则化参数γ和核函数形状参数σ2进行寻优并获得模型的最优解。

2 基于蝙蝠算法的最小二乘支持向量机模型

2.1 蝙蝠算法原理

蝙蝠算法是以蝙蝠利用超声波来探测猎物、避开障碍物、定位等随机搜索的生物学特征的方法，将蝙蝠个体搜索的过程模拟优化计算，将个体的优胜劣汰过程类比为优化和搜索过程中用好的可行解替代较差可行解的迭代过程，最终得到最优解，为了避免陷入局部最优，在算法中增强了局部搜索，即在最优解的附近设置随机飞行，产生局部新解，从而是先前全局和局部最优。该算法在求解前,需假设如下三个近似的或理想化的规则:

①蝙蝠运用回声定位来确定目标距离，并且能够采用一种特别的方式来判断猎物和背景障碍物的不同；

②各蝙蝠个体在xi位置以速度vi随机飞行，以其固定的频率fmin、可变波长λ和音量(响度)A0进行搜索目标。蝙蝠个体可依据自身与目标的距离来对其发射的脉冲波长(或频率)、脉冲发射率r进行调节；

③假设蝙蝠发出的音量(响度)的变化是从最大值A0到最小值Amin，A为正整数。

2.2 BA-LSSVM预测模型计算步骤

步骤2：设置参数：最大迭代次数N_iter=100，初始种群规模N=10，种群维数d=2，搜索脉冲频率范围Fmax和Fmin，蝙蝠种群的初始位置xi，xi是正则化参数γ和核函数形状参数σ2的二维向量：

x=xmin+rand(1,d)×(xmax-xmin)

(9)

步骤3：根据适应度函数值来确定当前最优解xbest，判断停止条件是否满足，若满足，则结束计算并输出最优解xbest；若不满足，则进行下一步。

步骤4：令xit为t时刻第i只蝙蝠的位置，vit表示该蝙蝠t时刻的速度，则蝙蝠的搜索脉冲频率、速度及位置的更新按照以下公式变化：

Fi=Fmin+(Fmax-Fmin)×μ

(10)

(11)

(12)

式中：Fi——搜索脉冲频率(Fmax为最大值，Fmin为最小值)；

μ∈[0,1]——均匀随机数。

步骤5：任意在上一步中获得的最佳位置种群中取一个xold，并对其进行随机扰动，则该蝙蝠的位置新的位置xnew按照以下公式变化：

xnew=xold+εAt

(13)

式中：ε——[-1,1]的随机数；

At——迭代次数为t的所有种群的平均响度。

步骤6：蝙蝠脉冲响度Ai和脉冲速率Ri会迭代进行而不断更新，生成随机数Rand，若Rand>Ai，且f(x)>f(xbest)，则接受xnew，脉冲响度和速率按照以下公式迭代变化：

(14)

(15)

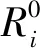
步骤7：按照适应度函数值的大小对种群进行排序，并得到当前的最优位置xbest’。

步骤8：判断停止条件是否满足，若满足，则结束计算并输出最优解xbest’；重复步骤(4)至(5)，直至最大迭代次数，输出全局最优参数，建立预测模型。

综上步骤，可将BA-LSSVM模型计算流程用图3表示，首先，将滑坡体积、高差、滑源区长度与宽度作为输入变量，滑坡纵向运动最大距离与横向最大堆积宽度作为因变量，选取的59组泾阳南塬为原始数据，通过蝙蝠算法寻求LSSVM的最优参数，最终通过BA-LSSVM模型进行预测。

图3 BA优化LSSVM计算流程图Fig.3 Calculating flow chart of the BA-LSSVM method

3 预测结果与分析

3.1 预测结果

从表1中选取前54组数据作为训练样本，剩余5组作为预测样本，根据2.2的计算流程进行预测计算。结果显示：纵向滑动距离L的最优正则化参数γ和σ2分别为82.899和3.435；横向堆积宽度的最优正则化参数γ和σ2分别为105.753和1.645。预测结果如图4所示。

图4 预测值与真实值对比图Fig.4 Comparison graph of predicted and true values

3.2 模型精度评价

为了评价预测该模型的准确性，分别选择RMSE(Root Mean Square Error,均方根误差)、MAPE(Mean Absolute Percentage Error,平均绝对百分比误差)和MSPE(Mean Squared Percentage Error，均方百分比误差)3个指标来评价，各评价指标计算公式如下：

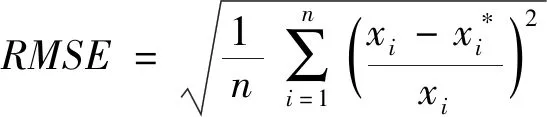
(16)

(17)

(18)

式中：xi——实际值；

xi*——预测值；

n——预测样本个数。

另外，为了验证本文的预测模型的优劣，建立基于多因素拟合的多元线性回归公式[16]：

L=-0.712 08H+0.000 181V+2.025 497Ls-

0.047 34Ws+99.146 252

(19)

W=0.091 87H+0.000 0285V-0.028 91Ls+

0.953 757Ws+3.607 367

(20)

各计算结果如表2所示。

表2 测试样本预测值及误差Table 2 The predicted values and errors of test samples

由表2可以看出，基于蝙蝠算法的最小二乘法的预测模型预测结果精度多元回归法有明显提高，可以用来预测该地区的滑坡致灾范围。

4 结语

本文通过蝙蝠算法寻找最小二乘支持向量机模型中的最优正则化参数γ和σ2，选取影响陕西泾阳塬边滑坡致灾范围的因素，分别对滑坡的致灾范围(纵向滑动距离L和横向堆积宽度W)进行预测，并且与多元线性回归方法的预测结果进行对比，结果表明本文构建的模型具有更高的预测精度和预测效果。在对泾阳南塬调查中发现，在塬边仍然发育许多横向裂缝，可近似的认为裂缝的长度为下次滑坡的滑源区宽度，并依此估算滑坡方量；通过地形测量可获得滑坡高差与滑源区长度，可运用本文建立的预测模型，对将要发生的滑坡致灾范围进行预测，达到防灾减灾的目的。