人体腰椎生物力学模型及损伤参数敏感性分析
2020-11-03唐亮郑佳佳李文熙程一鸣李润欣
唐亮 郑佳佳 李文熙 程一鸣 李润欣
(北京林业大学 工学院,北京 100083)
随着汽车工业的迅速发展,新型轿车所配备的乘员约束系统更为先进,能够更好地保护车内乘员。但是新型轿车在正面碰撞中产生胸腰椎骨折的事故率却逐年上升[1-3]。Pintar等[1]统计了1986年到2008年的数据,发现正面碰撞中腰椎骨折损伤几率逐年增加,且与车辆的出厂年份成正比。美国国家事故抽样系统(NASS)的统计数据表明每年约有2 000~4 000名乘客在正面碰撞中出现胸腰椎骨折并且受伤人数呈增长态势[2]。2000年后生产的车辆正面碰撞腰椎损伤人群数量是90年代生产车辆的2.5倍[3]。与旧车相比,新车碰撞减速度波形比旧车设计得更严格,以减少碰撞中防火墙对乘员舱的入侵。Adolph等[4]通过对德国事故调查数据库(GIDAS)的深入统计分析,指出座椅刚度及结构、碰撞减速度波形及膝部气囊可能会增加腰椎骨折风险,但并没有进行碰撞试验和数值模拟计算的验证。Tang等[5]通过数值模拟研究了碰撞波形与乘员腰椎轴向力之间的关系,研究表明碰撞波形的剧烈程度、碰撞波形峰值时刻的早晚,都会影响乘员腰椎轴向力峰值大小。同时新车配备了更先进的防下潜乘员约束系统(安全带腰带预紧器、肩带限力器、防下潜座椅、膝部气囊等)来防止乘员下潜,在Tang等[5]的研究中,发现防下潜措施与腰椎损伤之间存在着矛盾性,即在配备防下潜措施的情况下,腰椎轴向力会显著增加(P<0.05)。
在过去20年时间,针对人体脊椎损伤的研究热点主要集中于颈椎[6-9]以及胸椎上部[10-11]损伤,对腰椎段损伤并没有给予足够的重视。在相关汽车碰撞实验法规中,美国联邦机动车安全标准(FMVSS)、新车评价规程(NCAP)和高速公路安全保险协会(IIHS)也没有腰椎损伤的相关评价标准[1,12-13]。目前用于碰撞分析的人体有限元模型包括GHBMC和THUMS,其头部、颈部、胸部和下肢的碰撞生物力学特性通过了尸体实验验证[14],但其腰椎生物力学特性没有经过尸体试验验证,生物仿真度低,腰椎结构简单,无法预测碰撞中腰椎损伤的风险。
在汽车碰撞事故中韧带在脊柱整体的动态响应中起到了至关重要的作用。韧带附着于骨骼的活动部位,限制其大幅度相对运动,防止造成严重损伤。Pintar等[15]对38个真实人体腰椎的韧带进行了拉伸实验,实验得到的腰椎各个部分韧带的刚度数值离散性较大,如L1-L2的前纵韧带的刚度值为(32.4±13.0) N/mm。不同人体样本之间的韧带刚度值具有一定的差异,因此为了研究不同人体的腰椎损伤响应,需要对韧带刚度对腰椎损伤的影响进行研究。
韧带作为身体的软组织受到外界载荷作用很容易超过生理拉伸范围受损伤,尤其在动态冲击载荷的作用下韧带极易产生不可逆损伤。韧带的松弛区是由于韧带纤维束在未加载的情况下具有的初始波浪造成的[16],纤维束的初始波浪状态和断裂特性都随着个体的不同、关节位置的不同而不同,进而造成韧带整体力学性能的差异,从而对腰椎整体运动学与动力学响应造成影响。研究表明韧带在不同加载速率下具有不同的应力应变曲线,其具有应变率效应[17]。但是现有的腰椎有限元模型没有充分考虑韧带的失效区、松弛区以及腰椎在高速冲击下的动态响应[18-19]。多数研究中都将韧带简化为弹性材料,如GHBMC的腰椎模型中没有建立韧带,THUMS有限元模型中仅将韧带考虑为刚度可变但不可失效的一维弹簧单元。Schmidt等[20]对现有模型的韧带材料参数进行调整,建立了L4-L5段的腰椎功能单元,此模型具有较高的生物逼真度,但是其只包括腰椎功能单元,无法用以研究正面碰撞中的腰椎损伤。傅啸龙等[21]基于中国老年女性CT数据,建立了L1-S1腰椎段有限元模型,韧带采用非线性一维弹簧表达。以上模型都并未考虑韧带失效区、松弛区和应变率效应对于腰椎损伤的影响,这种计算机模型简化方法对腰椎损伤的影响还不清楚,因此研究韧带参数对研究腰椎损伤具有重要意义。
腰椎整体响应不仅与椎体和人体软组织的生物力学性能相关,还与各组织空间相对位置即人体腰椎曲率相关[22]。在汽车碰撞中,驾驶员以及乘员的姿态改变也会导致腰椎曲率的变形,进而导致在正面碰撞中腰椎承受轴向压缩载荷时其动力学与运动学响应产生变化。Stemper等[23]提出在汽车尾撞过程中,颈椎初始姿态不但会影响碰撞过程中韧带伸缩量并且会造成长期性挥鞭伤。Sato等[24]详细绘制了车内驾驶乘员在高速尾撞时,从乘员头部离开头枕到撞击,头部反弹压缩头枕150 ms内乘员脊椎的相对位置图。Naserkhaki等[25]研究了在矢状面内具有不同曲率的腰椎在前向弯曲和后向弯曲工况中的响应的差异,发现腰椎部位低突出曲率在前向弯曲中更为稳定,在后向弯曲中相比于正常曲率腰椎运动范围增加。高弯曲度腰椎在后向弯曲中明显降低了椎间盘压力,腰椎曲率较大影响着载荷位置以及量级,并且影响着后向弯曲工况腰椎运动学以及载荷分布。
为了研究腰椎损伤机理,通过生物力学实验数据拟合出符合人体韧带生理特征的韧带单元作为腰椎模型输入极为必要。在20世纪90年代,国外展开大量针对人体腰椎相关组织的研究,针对腰椎组织研究可分为4个层次:对腰椎部分组织的研究[15,26-27](如韧带、椎间盘及椎体中的皮质骨、松质骨和端板)、对腰椎主要功能段的研究[28]、对腰椎整体动态响应的研究以及对整人中的腰椎的动态响应的研究。目前文献提供了大量详尽的人体腰椎组织的材料参数,为腰椎有限元建模提供了数据支持。本研究中数据依托于医学工程研究的腰椎模型,并引入高速碰撞载荷下的腰椎组织材料应变率效应及失效准则。
本研究基于GHBMC腰椎模型的几何外形,建立包含有更准确的韧带参数的人体腰椎有限元模型。通过处理已发表论文中的实验数据,得到各种韧带的拉伸载荷曲线及其不同加载速率下对应的载荷拉伸曲线,以此来研究不同韧带的参数(韧带失效力、松弛区长度、应变率效应、韧带刚度)对于腰椎损伤的影响。同时本研究构建不同曲率的腰椎有限元模型,以分析腰椎曲率对于腰椎损伤的影响。
1 模型建立
1.1 人体腰椎生物力学模型的建立与验证
GHBMC模型具有比较真实的腰椎几何外形,因此本研究在GHBMC的基础上进行腰椎段有限元模型的建立与改进。GHBMC的腰椎模型如图1(a)所示,其椎体材料为不变形的刚体材料,椎间盘采用一层简单的壳单元表征。为了提高有限元腰椎模型的生物力学特性,在GHBMC几何模型的基础上改进后的腰椎模型如图1(b)所示。

(a) 压缩(试验)
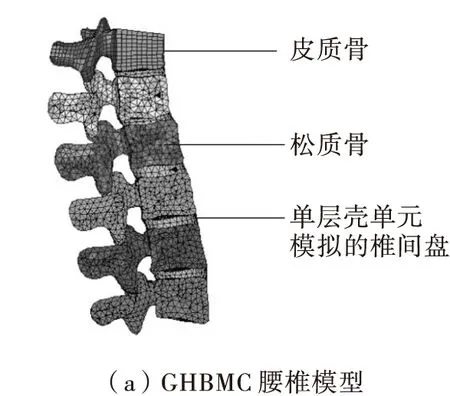
图1 GHBMC腰椎有限元模型和改进后的腰椎模型Fig.1 GHBMC lumbar spine model and modified lumbar spine finite element model
改进后的腰椎模型中椎间盘被分为基质、髓核和纤维环3个部分,在松质骨的外表面生成一层厚度为0.5 mm的壳单元代表皮质骨。在皮质骨之间建立了细致化的韧带模型,韧带包括前纵韧带、后纵韧带、黄韧带、小面关节囊韧带、棘间韧带、棘上韧带和横突间韧带。
腰椎生物力学有限元模型有64 388个单元和12 295个节点。基质、髓核和椎体为体单元,皮质骨为壳单元,纤维环和韧带为梁单元。松质骨和皮质骨采用LS-DYNA材料库中的98号材料进行描述,其有效失效应变分别定义为1.3%和0.94%[29]。皮质骨的弹性模量为11 740 MPa,松质骨的弹性模量为259 MPa。椎间盘端板采用弹性材料表征,弹性模量为200 MPa,椎体端端板采用98号材料进行描述,弹性模量为9 450 MPa。基质和髓核由27号材料进行描述,其中A和B是定义该材料的剪切模量的两个无量纲常数。在动态压缩速率为100 mm/s 的情况下,定义髓核和基质的A值分别为0.64和0.24,定义髓核和基质的B值分别为-0.16和-0.06。纤维环的力与位移曲线和SHIRAZI-ADL[30]的试验获得的曲线一致。椎间盘和相邻椎体之间通过CONTACT_TIEBREAK的方式进行连接。
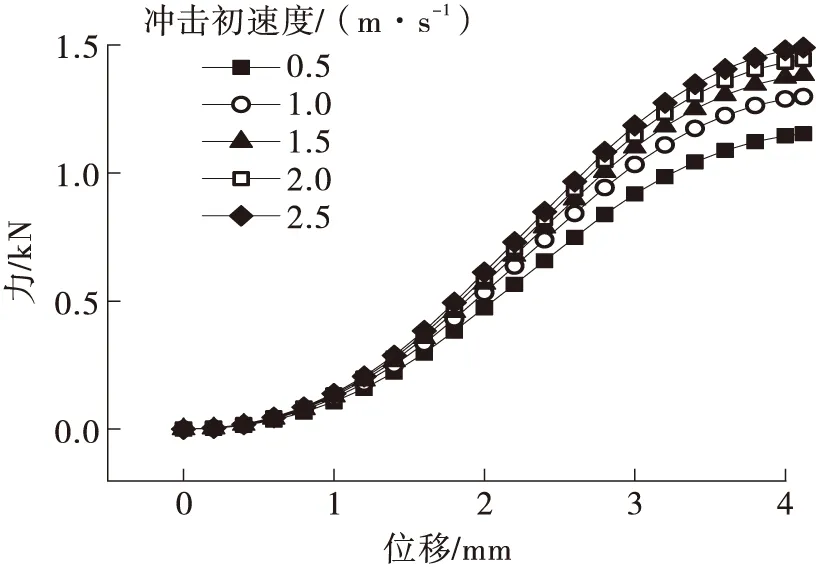
在第1.1节中,韧带材料是采用弹性材料表征的,即只考虑韧带应力应变曲线中的线性段。文献[15]中对腰椎各部分韧带进行了力学拉伸实验,获得了各个韧带的刚度值(见表1)。本研究中韧带采用1D单元表达,新建腰椎模型中各个韧带的刚度值等于实验中各个韧带的刚度值除以该部分所建立的1D韧带单元个数。
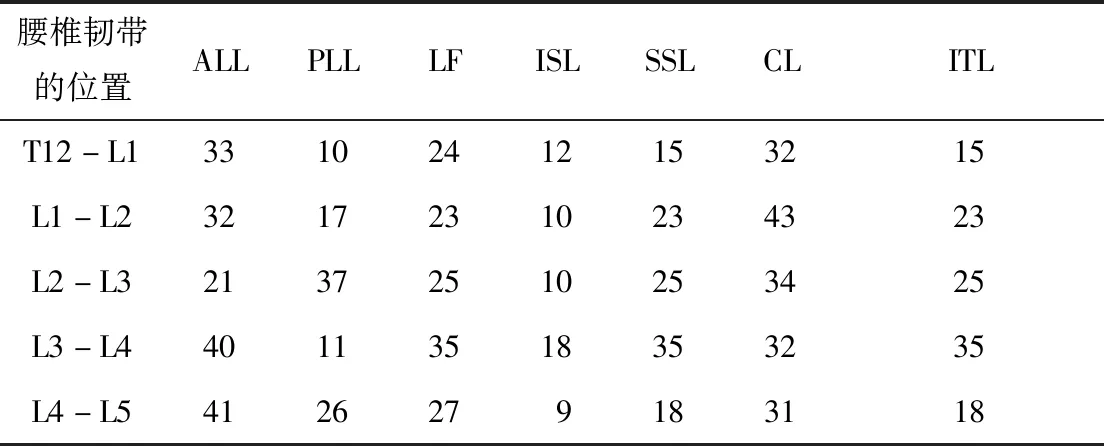
表1 人体腰椎韧带刚度值1)Table 1 Ligaments stiffness of human lumbar spine
通过与Demetropoulos等[31]的腰椎尸体实验数据进行对比来验证所建立腰椎模型静态加载的生物力学特性。仿真中腰椎姿态初始位置与实验中的保持一致(见图2)。对比6种工况下(压缩、前向剪切、后向剪切、侧向剪切、前向弯曲和侧向弯曲)的试验和仿真的结果。仿真工况与实验工况如图3所示,实验图中样本为混III假人的腰椎,仅作为工况示意图。
实验中人体脊柱T12上半部分、L5下半部分采取密封胶与上下平板进行固定连接。使用紧固螺钉将实验样本一端固定在实验平台上,在另一端施加载荷。压缩工况中,固定样本上端,在另一端加载;前向、后向和侧向剪切工况中,固定实验样本上端,对实验样本下端进行加载;前向、侧向弯曲工况中,固定模型下端,采用800 mm缆绳牵拉上端进行加载。各个工况的加载速率均为100 mm/s。所有实验样本均没有出现明显骨折现象。
在仿真模型中,腰椎段中T12上半部分和上平板固定连接,L5下半部分和下平板固定连接。仿真中各个工况的加载速率均为100 mm/s,与试验保持一致。6个工况下的仿真和试验一致,均未出现骨折现象。
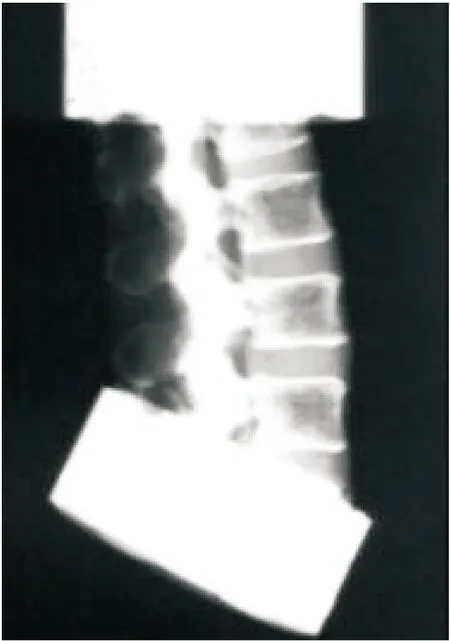
(a)实验中
在仿真中提取压缩和剪切工况下的力与位移曲线,提取弯曲工况下的弯矩与转角曲线,与试验数据进行对比(见图4)。Demetropoulos等[31]对10个真实人体腰椎段样本在各个加载工况下进行了实验,每个工况中的10条实验结果曲线的上边界与下边界围成的区域即为图4中该工况的阴影部分。若仿真结果曲线落在了各个工况的阴影区域,则证明仿真结果和实验结果是匹配的。图4结果表明,改进后腰椎模型的生物力学响应和尸体实验数据对比结果很好。
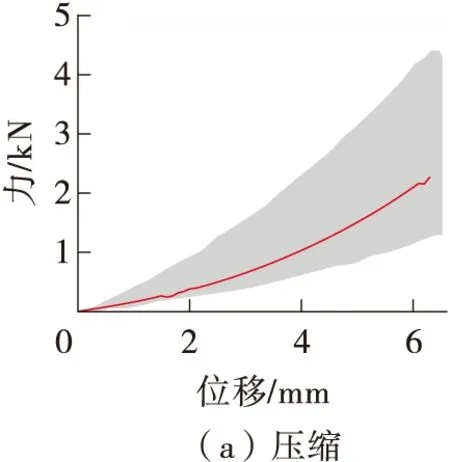
图4 不同工况中实验和仿真的腰椎载荷曲线对比[31]Fig.4 Comparison of load curves between experiments and simu-lations under various conditions[31]
除对静态载荷下腰椎的响应进行验证外,还对腰椎有限元模型的动态载荷下的响应进行了验证。本研究根据前期实验分别对人体腰椎段脊柱功能单元和整体腰椎段进行失效验证。
Duma等[32]在脊柱功能单元压缩破坏实验中将腰椎实验样本置于自然对齐的姿态,采用密封胶分别固定上下椎体的上半部和下半部,然后固定实验样本下端进行压缩实验,压缩速度为1 000 mm/s。在仿真中采用刚体-柔体的连接方式对上下椎体的上半部和下半部进行固定。约束下固定板的6个自由度,通过Boundary关键字给上固定块施加了恒定向下的1 000 mm/s的速度曲线。实验与仿真的对比如图5所示。
(a)脊柱功能单元压缩实验
仿真中和实验中的力与位移曲线如图6(a)所示,仿真模型计算结果与尸体实验结果非常吻合。图6(b)中显示的失效位置和失效特征与实验中结果一致,即骨折发生在上部椎体的下端板处。仿真结果表明,建立模型中腰椎脊柱功能单元具有和尸体实验一致的动态响应。

(a) 压缩工况载荷曲线
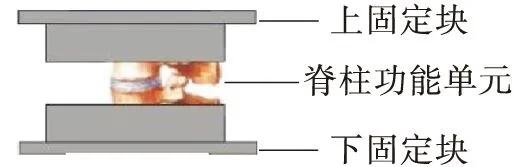
在人体脊柱腰椎段整体破坏性实验中[32],采取密封胶固定的方式对T12椎体上半部和L5椎体下半部进行固定。压缩实验过程中固定实验样本的下端,在腰椎上端施加向下的压缩载荷,压缩速度为1 000 mm/s。在仿真中采用刚体-柔体的连接方式对T12椎体的上半部和L5椎体的下半部进行固定。约束下固定块的6个自由度,通过Boundary关键字给上固定块施加了恒定向下的1 000 mm/s的速度曲线。图7为仿真模型与尸体实验对比图。

图7 人体腰椎段尸体实验与仿真模型对比Fig.7 Comparison between cadaver experiment and finite element model of human lumbar spine
仿真模型与尸体实验结果对比如图8所示。实验中分别对一名男性样本和一名女性样本的腰椎进行了动态加载。图8中实验1为女性样本实验,实验2为男性样本实验。仿真模型为对新建的生物力学腰椎模型进行动态压缩得到的结果曲线。
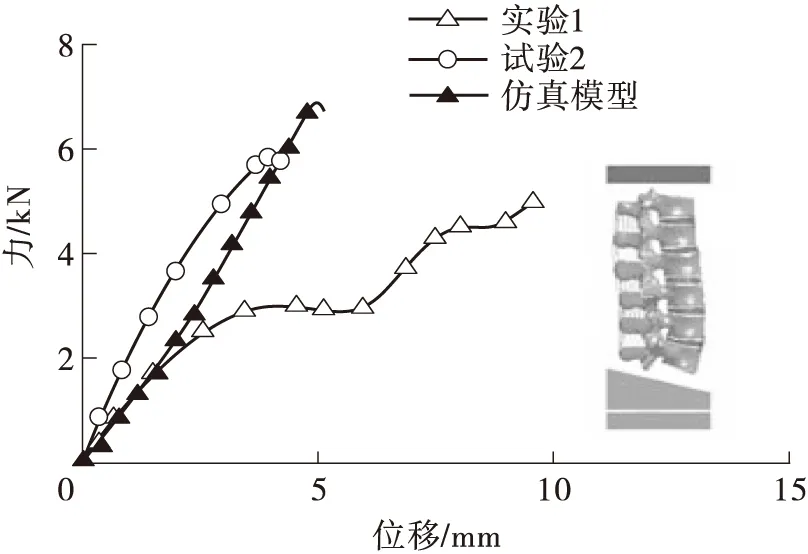
(a)力与位移曲线对比
仿真结果中力与位移曲线和弯矩与位移曲线与实验结果吻合良好(如图8(a)和图8(b)),失效特征与实验研究基本一致(图8(c)和图8(d))。实验中和仿真中腰椎载荷和弯矩曲线与动态加载下腰椎失效位置的吻合验证了整体腰椎段有限元模型动态载荷下的动态响应。实验中T12椎体前部发生了骨折,在仿真模型计算过程中,除T12椎体前部外,L3椎体下部也发生了端板处失效断裂。由于实验中样本数量很少(男性和女性各一个),因此判断骨折位置并不完全相同,但是实验和仿真中T12椎体前部都发生了骨折。
1.2 仿真平台建立
根据Stemper等[33]搭建的腰椎承受轴向冲击的试验平台,本研究搭建了腰椎承受垂直冲击载荷的仿真平台。实验中腰椎肌肉以及周围组织被清除,仅剩下椎体、韧带以及完整椎间盘。腰椎上端面与下端面由聚甲基丙烯酸甲酯(PMMA)材料固定以便于安装至加载装置。在安装过程中腰椎L2-L3椎间盘部位保持水平以控制腰椎整体的初始姿态。加载装置由两个水平平板组成,腰椎椎体在承受冲击作用前由底部平面支撑,在承受冲击载荷时加载装置依靠重力自由下落直到腰椎接触到整个装置下方的产生脉冲波形的泡沫材料。
如图9所示,连接于上部平台的上部质量模拟上部肢体、躯干以及头颈部质量。上部平台与上部固定装置之间接触形成圆柱状加载装置。初始冲击速度加载于上部质量、平台以及冲击圆柱整体,最终加载通过腰椎样本,底部固定装置加载于底部泡沫垫子。泡沫材料尺寸长×宽×高为30 cm×45 cm×65 cm密度16 kg/m3,上部质量块32 kg代替上肢质量。冲击初速度设置为0.5 m/s。
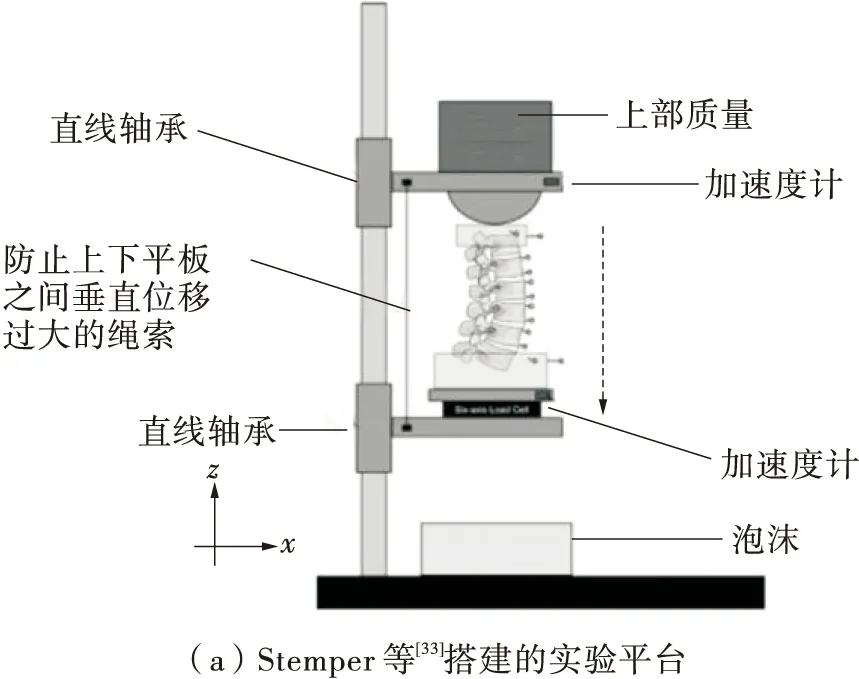
图9 轴向冲击工况的试验和仿真平台Fig.9 Setup for axial impact condition in experiment and simulation
1.3 韧带材料参数
韧带的力与位移曲线如图10所示,主要分为3个阶段:松弛区,线性区和损伤区[34-35]。根据腰椎韧带实验数据拟合高生物逼真度的韧带材料载荷曲线时,按照这3个阶段进行分别拟合。首先求解韧带线性区的刚度值,再分别对3个阶段的韧带载荷曲线进行拟合,最后求解韧带应变率相关的动态比例因子。
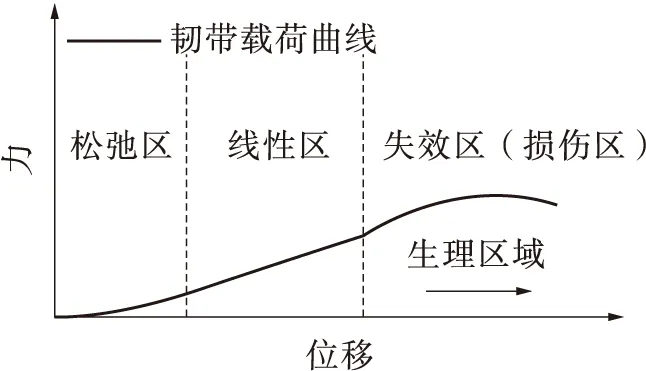
图10 韧带松弛区的介绍[34]Fig.10 Introduction of the ligament relaxation zone[34]
韧带材料的刚度值已经在第1.1节的表1中体现。Pintar等[15]对韧带进行拉伸实验,获得不同人体腰椎的每条韧带的力与位移曲线,再基于最小二乘法求得该结果曲线的拟合直线,所求得直线的斜率即为韧带的刚度值。为获得韧带静态力与位移曲线,根据式(1)-(3),采用Mattucci等[35]的实验数据进行拟合,拟合结果如图11(有松弛区)和图12(无松弛区)所示。
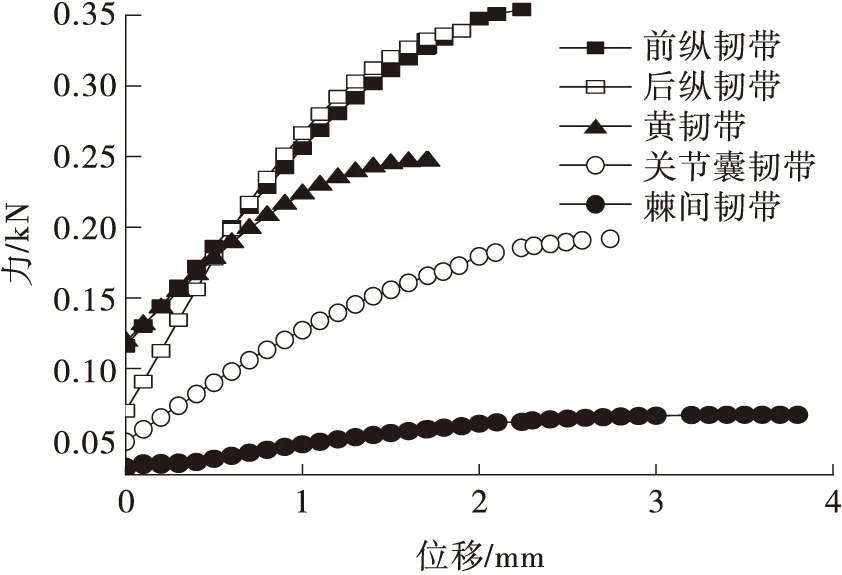
图12 腰椎韧带去除松弛区载荷-位移曲线Fig.12 Load-displacement curves for lumbar ligaments without initial slack

图11 腰椎韧带载荷-位移曲线Fig.11 Load-displacement curves for lumbar ligaments
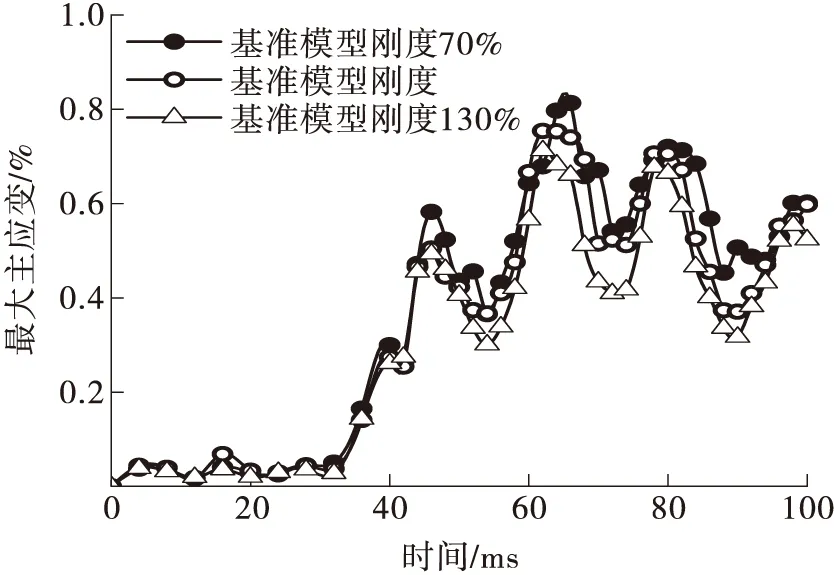
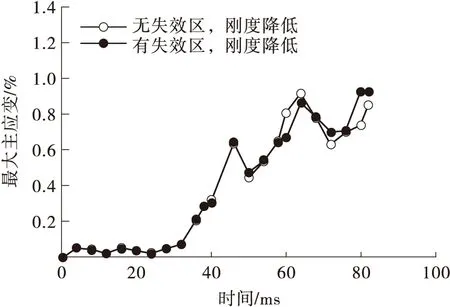
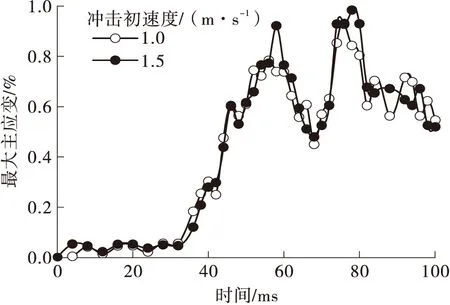
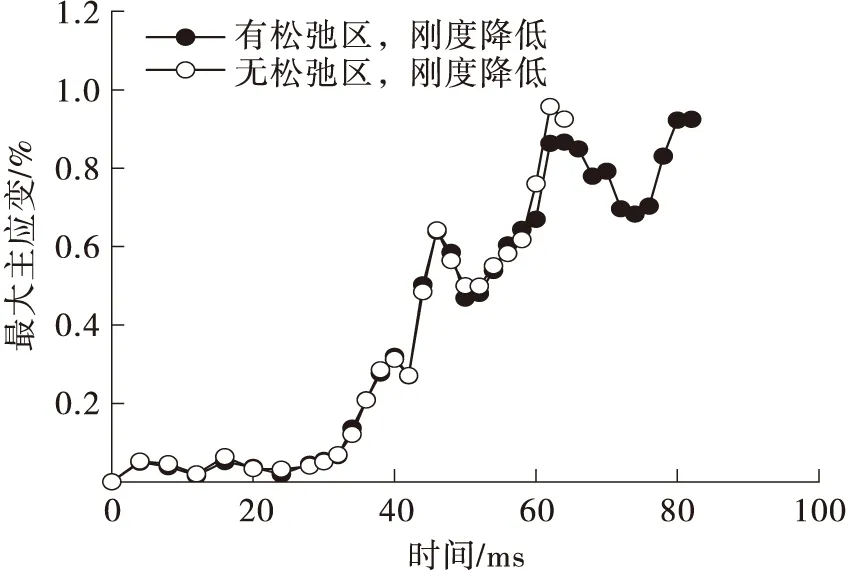
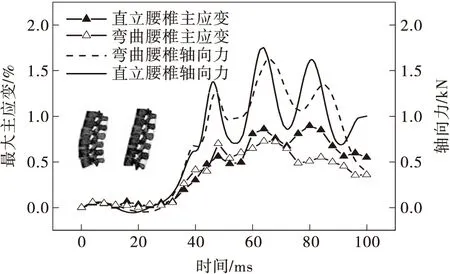
松弛区(d F=C3(exp(C4d)-1)dm* (1) 线性区(d>d*): F=Fd*+(d-d*)C5 (2) 损伤区(d>t*): F=Md3+Nd2+Qd+P (3) 式中:d为韧带位移,F为韧带承受的轴向载荷,d*为韧带松弛区域的结束点位移,C3、C4和m*为韧带松弛区域常数,Fd*为过度点的承受载荷,C5为韧带线性区的斜率即刚度,拟合损伤区域采用三次多项式进行拟合,其中t*代表线性区域与损伤区域的结合点处位移量,M、N、P、Q为多项式拟合常数。在损伤区域韧带受载荷曲线会达到峰值,其中Ffall和dfall代表失效点的峰值力和位移。各韧带的拟合参数如表2所示。 表2 韧带力与位移曲线拟合参数Table 2 Fitted parameters for lumbar spine ligaments force-displacement curves 为确定不同加载速率下韧带的刚度值与准静态韧带刚度值的比例(简称动态比例因子k),本研究采用了Yoganandan等[17]研究韧带较高变形速率下的实验数据。以黄韧带和前纵韧带为例,整理9 mm/s冲击速度下韧带刚度(韧带静态刚度)和韧带在25、250和2 500 m/s冲击速率下的刚度值。在对数坐标系下拟合得到前纵韧带和黄韧带在不同冲击速度下的动态比例因子,得到拟合公式(4)。式中,x为冲击速度,y为动态比例因子。不同冲击速率下韧带的力与位移曲线通过式(5)计算得到。 y=0.668 3 lnx-0.417 3 (4) F=f(ΔL)k (5) 式中,F为韧带动态力与位移曲线,f(ΔL)为静态力与位移曲线,k为动态比例因子。得到的前纵韧带在不同冲击速度下的力与位移曲线如图13所示。 图13 前纵韧带在不同冲击速度下的力与位移曲线Fig.13 Anterior longtitudinal ligament force-displacement curves under various loading velocity 本研究中对腰椎曲率的定义参考Chabert[36]给出的定义。在人体的侧视图中,腰椎每个椎体的上下端板的最前端和最后端的点组成了腰椎椎体的几何四边形,该几何中心点即为每个腰椎椎体的中心,5个椎体的中心连接成平滑的曲线即为腰椎姿态曲线,其曲率的大小代表了腰椎弯曲程度。曲率越大,腰椎越弯曲,曲率越小,腰椎越竖直。 本研究根据真实人体腰椎段的扫描数据,调整生物力学腰椎模型中各个椎体的位置与姿态,获得直立姿态腰椎和弯曲姿态腰椎,如图14所示。 (a)直立腰椎 由于绝大多数椎体损伤是由于椎体骨折断裂造成的,因此选取最大主应变作为评估腰椎损伤的主要判据[6]。 以第1.1节建立的腰椎轴向冲击平台中腰椎模型作为基准模型,分别增加或减少韧带刚度值,以0.5 m/s的冲击速率进行加载。提取轴向冲击过程中腰椎椎体的最大主应变值,如图15所示。 图15 不同腰椎韧带刚度下的最大主应变对比Fig.15 Comparison of maximum principal strains under various lumbar ligament stiffnesses 3种韧带刚度下,腰椎椎体的最大主应变随着时间的变化曲线具有4个明显的峰值(45、65、80和95 ms)。在这4个峰值时刻,刚度降低30%的腰椎椎体最大主应变大于基准模型中的腰椎椎体最大主应变,刚度比基准模型刚度高30%的腰椎椎体的最大主应变是最小的。以65 ms左右为例,腰椎最大主应变达到峰值,低刚度模型中腰椎椎体最大主应变高达0.82%,基准模型中最大主应变为0.75%,高刚度模型中最大主应变为0.70%。因此腰椎韧带刚度降低,乘员腰椎最大主应变明显增大。 不同人体之间的韧带刚度值具有一定的差异。在其他条件一致的情况下,韧带刚度越低,腰椎椎体的最大主应变越大,因此在汽车乘员保护数值研究过程中,建立不同体征参数的人体韧带模型时,应当赋予其准确的韧带刚度参数,才可以对乘员腰椎损伤进行更为准确的预测。 对比考虑韧带失效区和不考虑失效区的腰椎椎体平均最大主应变的差异,结果见图16。 (a)低刚度时有失效区和无失效区的仿真结果 在低刚度工况中,50 ms之前考虑韧带失效区和不考虑韧带失效区的曲线基本吻合,50 ms之后两条曲线的差异开始出现。考虑韧带失效区的腰椎最大主应变峰值出现在82 ms,为0.93%,不考虑韧带失效区的腰椎最大主应变峰值出现在64 ms,为0.91%。考虑腰椎韧带失效区的腰椎最大主应变略高于不考虑韧带失效区的最大主应变。 在高刚度工况中,50 ms之前考虑韧带失效区和不考虑韧带失效区的曲线基本吻合,50 ms之后两条曲线的差异开始出现。考虑韧带失效区的腰椎最大主应变峰值出现在82 ms,为0.98%,不考虑韧带失效区的腰椎最大主应变峰值出现在64 ms,为0.92%。考虑腰椎韧带失效区的腰椎最大主应变高于不考虑韧带失效区的最大主应变。 两种刚度工况下,考虑韧带失效区的腰椎最大主应变峰值出现时刻都晚于不考虑韧带失效区的腰椎最大主应变。不考虑韧带失效区的腰椎最大主应变峰值出现时刻为64 ms,考虑韧带失效区的腰椎最大主应变峰值出现时刻为82 ms。 结果表明,在韧带刚度相同情况下,考虑韧带失效行为的腰椎模型最大主应变明显高于不考虑韧带失效行为的腰椎最大主应变,简单地将韧带简化为不可失效的弹簧单元进行仿真会低估腰椎的最大主应变值,因此在腰椎有限元仿真中应该对于韧带失效行为给予重视,考虑韧带失效行为有助于提高预测腰椎损伤的准确度。 为研究腰椎韧带应变率对于腰椎动态响应的影响,分别将1.0 m/s和1.5 m/s冲击初速度的模型置于仿真平台上。结果表明,冲击初速度为1.5 m/s的腰椎最大主应变高于初速度为1.0 m/s的腰椎最大主应变(见图17)。60 ms左右,冲击初速度为1.5 m/s的冲击工况中腰椎平均最大主应变出现急剧的增加(从0.78%骤增到0.93%),此值远高于冲击初速度为1 m/s工况中的腰椎平均最大主应变(0.78%)。80 ms左右,两种工况中的腰椎最大主应变峰值差异不大,1.5 m/s工况中的腰椎最大主应变(0.98%)略高于1.0 m/s冲击工况中的腰椎最大主应变(0.94%)。 图17 不同冲击速度下腰椎最大主应变对比Fig.17 Comparison of maximum principal strains under diffe-rent impact velocity 随着冲击初速度增加,腰椎最大主应变峰值增加,因此正面碰撞中减小腰椎轴向冲击初速度是保护腰椎的方法之一。 将考虑韧带松弛区域和不考虑韧带松弛区的腰椎有限元模型加载于仿真平台中。 如图18所示,在韧带刚度保持相同的情况下,考虑松弛区的腰椎有限元模型最大主应变高于不考虑韧带松弛区的腰椎最大主应变。 (a)低刚度时有松弛区和无松弛区的仿真结果 在低刚度韧带的腰椎模型中,考虑韧带松弛区的腰椎最大主应变峰值出现在82 ms,峰值为0.92%;不考虑韧带松弛区的腰椎最大主应变峰值出现在62 ms,峰值为0.96%。在高刚度韧带的腰椎模型中,考虑韧带松弛区的腰椎最大主应变峰值出现在82 ms,峰值为0.98%;不考虑韧带松弛区的腰椎最大主应变峰值出现在68 ms,峰值为0.88%。同时,两种刚度工况下,考虑韧带松弛区的腰椎最大主应变峰值出现时刻都晚于不考虑韧带松弛区的腰椎最大主应变。考虑韧带失效区的腰椎最大主应变峰值出现时刻为82 ms左右,不考虑韧带失效区的腰椎最大主应变峰值出现时刻为60~70 ms。 综上所述,韧带松弛区的考虑影响了腰椎在轴向冲击下的响应,包括腰椎最大主应变峰值和峰值时刻的早晚。松弛区是腰椎韧带中真实存在的区域,不考虑韧带松弛区会低估腰椎椎体的最大主应变峰值,因此对韧带松弛区的考虑有助于提高腰椎的生物逼真度,从而对腰椎椎体的最大主应变进行更为准确的预测。 弯曲腰椎和直立腰椎的0.5 m/s的轴向冲击速度下的损伤响应曲线如图19所示。在0.5 m/s的冲击速度下,弯曲腰椎的最大主应变明显小于直立腰椎的最大主应变,弯曲腰椎轴向力峰值也比直立腰椎轴向力峰值小。 图19 不同腰椎曲率下腰椎最大主应变和轴向力曲线对比Fig.19 Comparison of maximum main strains and axial force under different lumbar curvatures 弯曲腰椎的最大主应变发生在48 ms,腰椎椎体最大主应变为0.70%,直立腰椎的最大主应变发生在80 ms,腰椎椎体的最大主应变为0.87%。 弯曲腰椎的最大轴向力发生在66 ms,腰椎最大轴向力为1.60 kN,直立腰椎的最大轴向力发生在63 ms,腰椎椎体的最大主应变为1.75 kN。 综上,汽车碰撞中人体受到轴向冲击时,腰椎姿态为弯曲姿态时,人体腰椎最大主应变峰值和轴向力峰值都会降低,因此在对乘员腰椎进行保护时,可以考虑通过匹配乘员约束系统参数使得人体腰椎姿态为弯曲腰椎姿态,从而实现乘员腰椎保护的目的。 在腰椎有限元模型的建立中将韧带简化为不可失效的一维弹性体材料,不能真实反映人体腰椎的运动学和动力学响应。本研究通过处理已发表的实验数据,拟合出韧带的生物力学曲线,考虑了韧带的松弛区、线性区和失效区的载荷位移特性,还考虑了韧带应变率对韧带载荷曲线的影响,保证了腰椎韧带的生物力学特性,并将其输入腰椎有限元模型。通过建立轴向冲击平台模拟腰椎在正面碰撞中的响应,对比腰椎韧带在不同刚度下的腰椎损伤风险,发现韧带刚度越小,椎体发生失效的风险越高。对比不考虑韧带松弛区和考虑了韧带松弛区的仿真中腰椎最大主应变峰值,发现考虑韧带松弛区的腰椎模型损伤风险明显高于不考虑松弛区长度的腰椎模型。对比不考虑韧带失效区和考虑了韧带失效区的仿真中腰椎最大主应变峰值,发现考虑韧带失效区的腰椎模型损伤风险明显高于不考虑失效区长度的腰椎模型。对比不同冲击速度下的腰椎损伤的响应的差异,发现在高冲击速度工况下,韧带受到损伤的风险更大。因此在有限元仿真中应重视韧带生物力学行为并保持其完整性。在承受垂直载荷时,直立腰椎相比于弯曲腰椎承受更大的轴向力,随着冲击速度增加腰椎受到的轴向力与最大主应变有明显提高。直立腰椎在正面碰撞中垂直冲击载荷工况中有更高的损伤风险,这有助于指导乘员约束系统的设计。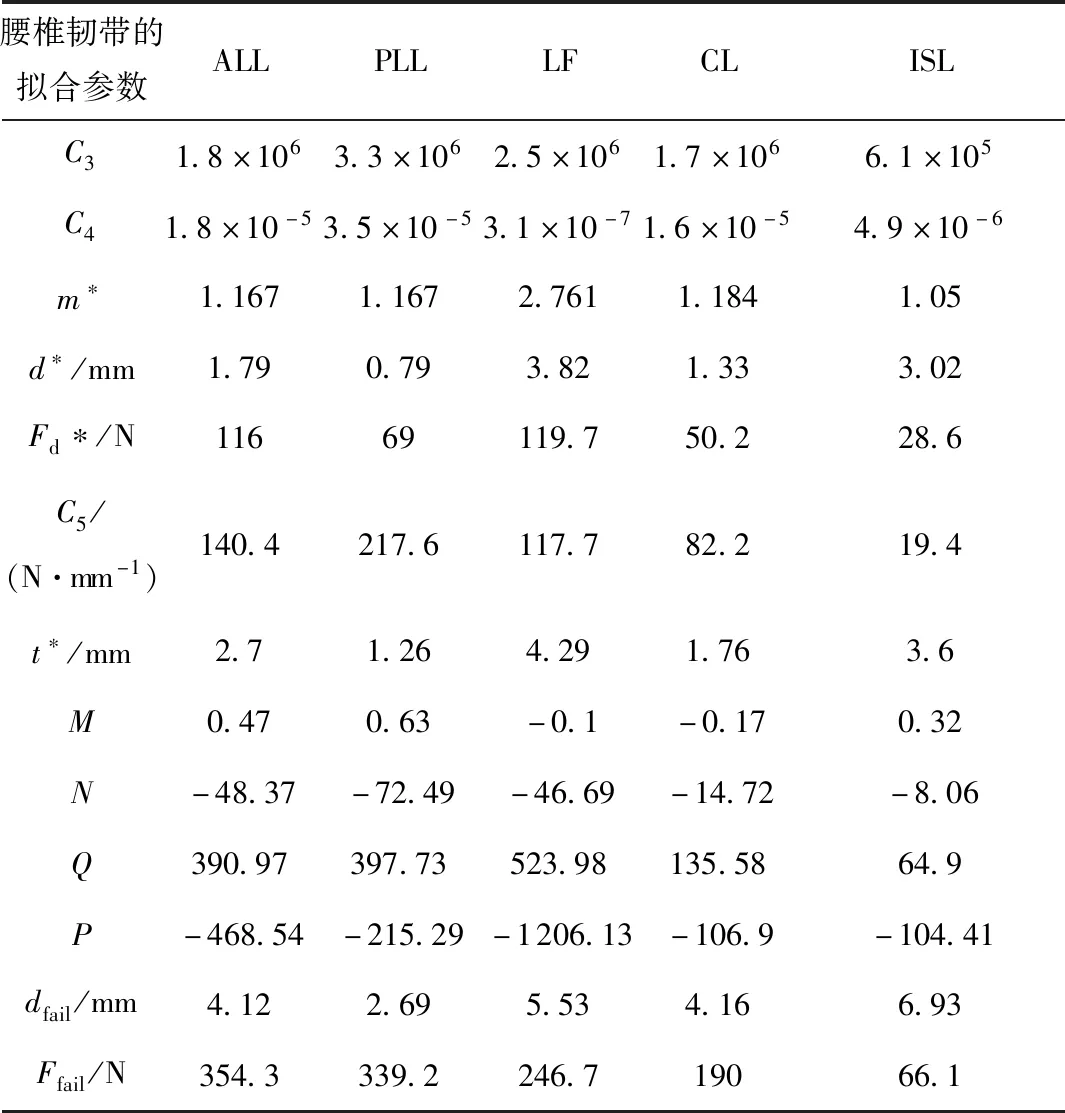
1.4 腰椎曲率

2 仿真与结果
2.1 韧带参数的影响
2.2 腰椎曲率的影响
3 结论
