基于伽马范数最小化的图像去噪算法

王洪雁，王拓，潘勉，汪祖民

（1.浙江理工大学信息学院，浙江 杭州 310018；2.大连大学信息工程学院，辽宁 大连 116622；3.五邑大学智能制造学部，广东 江门 529020；4.杭州电子科技大学电子信息学院，浙江 杭州 310018）

1 引言

数字图像在采集和传输过程中不可避免地受到噪声污染，从而造成图像细节丢失和质量下降，进而影响后续处理[1-2]。图像去噪的目的则是从噪声图像y中尽可能准确地恢复原始图像x，并保留边缘、纹理等重要细节特征。去噪问题退化模型可表示为y=x+v，其中，v可假设为均值为0、方差为的高斯白噪声。由于图像去噪的不适定性，利用表征图像统计特征的先验知识去噪显得尤其重要[3-4]。

近年来，众多图像降噪算法相继被提出，其大致可分为以下两类：基于局部先验的方法和基于非局部自相似（NSS,nonlocal self-similarity）先验的方法。基于局部先验的方法主要包括基于小波收缩（WS,wavelet shrinkage）[5]、全变分（TV,total variation）[6]和基于模拟退火的改进图像去噪（PID,progressive image denoising）[7]。然而，上述方法仅考虑局部先验知识，忽视非局部图像块间相似性先验信息，从而导致算法的去噪性能较差。非局部自相似先验可表述为给定图像某局部块，利用该图像非局部相似块之间的线性相关特性，搜寻与给定图像块相似的其他局部块。实践表明，NSS作为先验信息，在图像恢复任务中效果甚佳[8]。基于此，文献[9]提出一种非局部均值（NLM,nonlocal means）去噪算法，通过对相似图像块加权平均，可获得较好的去噪性能，但当噪声等级较高时，由于相似图像块包含大量噪声，从而导致去噪图像存在大面积模糊现象。针对此问题，文献[10]提出一种三维块匹配（BM3D,block matching 3D filtering）算法，将具有相似结构的2D图像块构造为三维数据，而后联合去噪来改善去噪性能，但较高时间复杂度限制了其实际应用。基于此，文献[11]提出一种非局部集中稀疏表示（NCSR,non-locally centralized sparse representation）算法，将相似图像块构造为矩阵，利用组稀疏方法改善去噪性能。然而，该算法所得去噪图像存在关键细节模糊等问题[12]。针对以上问题，研究人员注意到将非局部相似图像块以向量形式构造为矩阵会具有低秩特性及稀疏奇异值[13]，因而可以考虑利用低秩先验信息提升去噪性能。基于此，文献[14]提出一种核范数最小化（NNM,nuclear norm minimization）算法，利用核范数近似秩函数来构建低秩去噪模型，从而获得较好的去噪性能。然而该算法均衡处理各个奇异值，忽视了各奇异值不同程度地反映图像纹理等先验信息这一基本事实，从而导致去噪性能提升有限。针对此问题，文献[15]提出一种加权核范数最小化（WNNM,weighted nuclear norm minimization）算法，利用加权核范数近似秩函数，通过对奇异值赋予不同权值来改善去噪性能。然而，利用核范数近似秩函数将过度惩罚较大奇异值，从而导致去噪问题，只能获得次优解。此外，在网络结构及学习算法的驱动下，卷积神经网络（CNN,convolutional neural network）在图像去噪领域的应用受到越来越多的关注[16]。其中，Zhang等[17]基于残差学习理论提出去噪卷积神经网络（DnCNN,denoising convolutional neural network），其通常针对单个噪声水平学习特定模型，因而在处理包含不同噪声水准图像时需要生成多去噪模型，由此显著增加了网络复杂度，从而限制了此网络的实际应用。针对此问题，Zhang等[18]通过将噪声水平图及含噪图像作为网络输入，提出快速灵活去噪卷积神经网络（FFDNet,fast and flexible denoising convolutional neural network）以处理不同噪声水准及空域变化噪声，由于输入噪声水平图能够灵活权衡去噪程度及图像细节保持水平，因而此网络可对实际图像实现有效去噪。必须指出的是，尽管基于CNN的去噪方法行之有效，然而其面临特性重用问题，并且无法充分利用层数增加和大卷积核所导致的巨量参数，因而导致此类模型去噪性能提升有限[19]。

针对上述问题，基于可近乎无偏近似秩函数的非凸伽马范数（γ-norm）[20]及低秩去噪模型，本文提出一种基于非凸伽马范数最小化的图像去噪算法。所提算法首先利用结构相似性（SSIM,structural similarity）搜索相似图像块，避免传统方法相似图像块搜索不准确；然后利用伽马范数近乎无偏的近似矩阵秩函数以构建低秩去噪模型，从而解决传统秩函数近似方法估计精度较差的问题；最后基于奇异值分解对此非凸问题进行求解。仿真结果表明，与现有主流PID、NLM、BM3D、NNM、WNNM、DnCNN和FFDNet算法相比，所提算法可较显著地消除高斯噪声，且可以较高精度恢复原始图像细节。

2 低秩去噪模型

对所有重叠块执行上述操作并重组，即可构建原始图像。然而，核范数为有偏估计量，其近似秩函数可能过惩罚较大奇异值，从而导致核范数最小化问题无法获得最优解，进而降低去噪性能[24]。针对此问题，本文采用非凸伽马范数代替核范数以获得秩函数近乎无偏估计，进而改善低秩去噪性能。

3 所提图像去噪算法

本节首先提出一种自适应非局部相似图像块搜索方法，然后简要介绍伽马范数，并基于最小化非凸伽马范数来构建图像去噪模型，最后利用奇异值分解对所得优化问题进行求解。

3.1 自适应相似图像块搜索方法

传统基于欧氏距离的非局部相似图像块搜索方法未考虑图像块的结构相似性，从而导致非局部相似图像块搜索不准确[25]。为提高相似图像块搜索准确度，本文提出一种基于SSIM的自适应相似图像块搜索方法。SSIM是一种综合图像相似性的评价指标[26]，考虑图像间亮度、对比度和结构3 个不同特性，可较好评价两幅图像的相似程度。给定两幅图像x和y，SSIM定义为

自适应相似图像块搜索方法的主要思想简述如下：给定当前图像块yi和目标数据集，计算当前图像块与目标数据集各图像块的SSIM，并据此搜索与当前图像块最相似的m个图像块。其中，相似块数m需根据噪声等级自适应确定。然后将各相似图像块转换为列向量，并按相似度降序自左向右依次排列以组成相似图像块矩阵Yi，构建过程如图1所示。

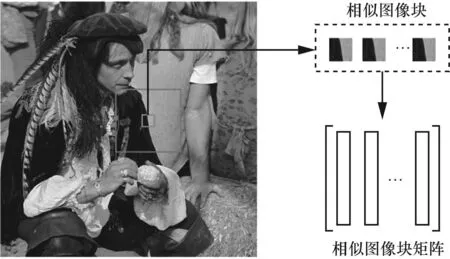
图1 相似图像块矩阵构建过程

综上所述，所提相似图像块搜索方法可充分利用图像非局部自相似的先验信息，提高相似图像块的搜索准确性。基于所获得相似图像块Yi，本文所提基于伽马范数最小化的图像去噪模型如3.2节所述。

3.2 伽马范数最小化模型

伽马范数是非凸MCP（minmax concave plus）函数的矩阵扩展，相比有偏估计核范数，其近乎无偏近似秩函数[27]。设矩阵X的奇异值分解为X=U ΣVT，其中，U=[u1…un]，V=[v1…vn]，Σ=diag(λ1…λn)，且λ1≥ …≥λn≥ 0，则伽马范数可定义为[20]

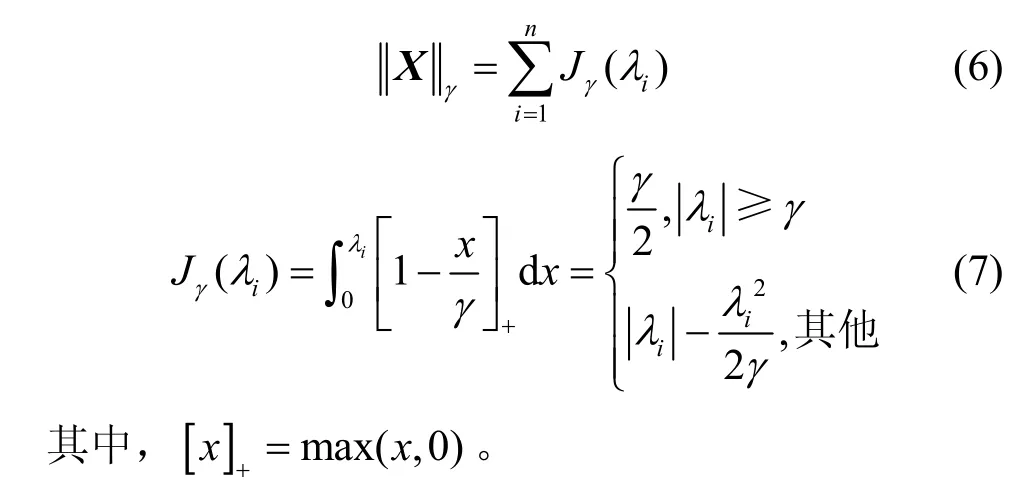
基于伽马范数可近乎无偏地近似秩函数的特性，本文用其替换式(1)中的低秩项，构建非凸伽马范数最小化去噪模型，可表示为

3.3 所提非凸模型求解

为便于表述，令X=Xi，Y=Yi，则优化问题式(8)的解的推导过程为

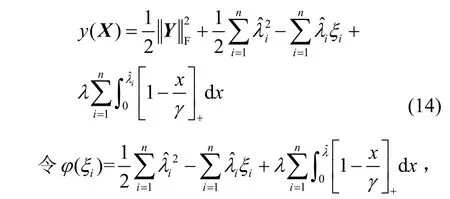
由于式(14)右端第一项与待优化变量X无关，则y(X)关于X的最小化问题等价于ϕ(ξi)关于ξi的最小化问题，由此ϕ(ξi)可重新表示为

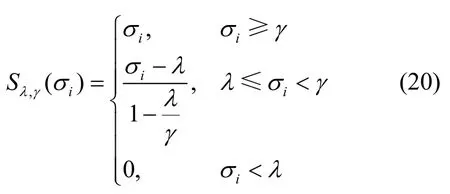
对各重叠图像块依次求解上述优化问题，即可求得所有去噪相似图像块矩阵{Xi},i=1,2,…,n，进而基于文献[15]图像块重组方法重构去噪图像x。实际应用中，可重复迭代以上步骤以获得较好的去噪性能。综上所述，基于非凸伽马范数最小化的图像去噪算法如算法1 所示，其中，步骤3)迭代正则化过程用以改善算法的去噪性能[28]。

算法1基于非凸伽马范数最小化的图像去噪算法

4 实验仿真及分析

实验基于标准图像库中如下6 幅图像（如图2 所示）：256 像素×256 像素Monarch、720 像素×576 像素Boats、512 像素×512 像素Lena、512 像素×512 像素Pepper、256 像素×256 像素House和720 像素×576像素 Barbara，采用PID[7]、NLM[9]、BM3D[10]、NNM[14]、WNNM[15]、DnCNN[17]和FFDNet[18]作为对比算法，分别从去噪性能和运行时间两方面验证所提算法的有效性。实验环境为Intel Core i7-8700，主频为3.70 GHz，内存为16 GB，操作系统为Windows 10，仿真软件为Python3.6。

为定量评估所提算法的去噪性能，本文采用文献[29]所定义的峰值信噪比（PSNR,peak signal to noise ratio）作为评价指标，即

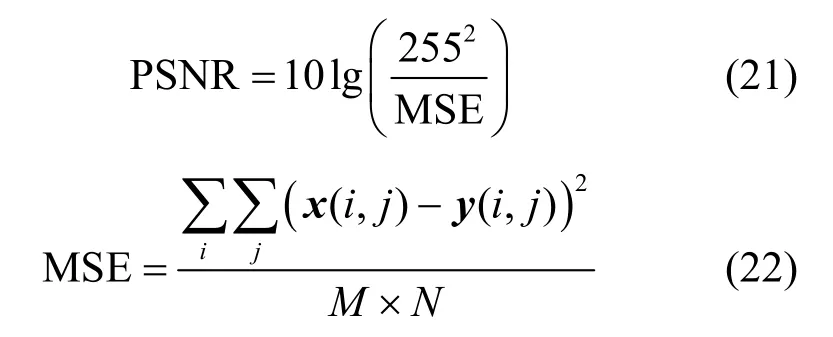
其中，MSE 表示均方误差（mean square error），M×N为两幅图像x和y的尺寸。

4.1 参数设置

依据实验，确定搜索窗口尺寸L×L为30 × 30，图像块尺寸、相似图像块数m及算法迭代次数K需根据噪声等级自适应确定。对于噪声方差为σn≤ 20、20<σn≤ 40、40<σn≤ 60和σn>60的噪声图像，图像块尺寸分别设为6 × 6、7 × 7、8 × 8和9 × 9，相似图像块数m分别设为70、90、120 和140。相应地，迭代次数K分别设为8、12、14 和14。参数δ、λ和γ分别设为0.1、0.001 和100。此外，DnCNN以及FFDNet的参数设置类似于文献[17-18]，不同的是，此二者皆基于文献[17]所用数据集中所选的200 幅图像进行20 次迭代训练。

4.2 去噪性能

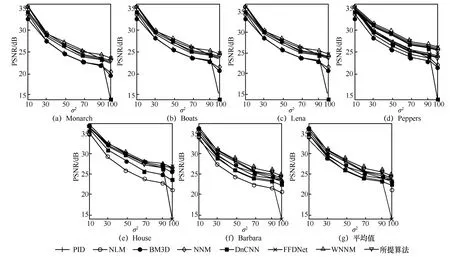
图3 各测试图像条件下不同算法所得PSNR 随噪声方差的变化曲线

表1 不同去噪算法PSNR 对比

6 幅测试图像分别添加均值为0、方差分别为σn=10,30,50,70,90,100的高斯白噪声来生成噪声图像。基于所得噪声图像，PID、NLM、BM3D、NNM、WNNM、DnCNN、FFDNet及本文所提算法所得PSNR随噪声方差的变化曲线如图3 所示。不同测试图像及噪声方差条件下所得PSNR的具体数据如表1 所示（由于篇幅限制，本文只列出σn=10,30,50,100条件下的去噪结果），各实验最高PSNR用粗体表示。由图3 及表1 可知，NLM去噪性能不明显，这是因为NLM仅对相似图像块加权平均，而没有考虑噪声本身特性；PID基于全域搜素的模拟退火算法进行去噪，因而去噪效果稍好于NLM；NNM和WNNM考虑了含噪图像的低秩特性，因而可获得较好的去噪效果，且由于WNNM对含噪图像奇异值差异性加权充分利用图像先验信息，从而使其降噪效果优于NNM；BM3D由于利用了相似图像块结构约束联合去噪，从而使其在非学习算法中脱颖而出，去噪效果明显优于上述算法。再者，基于数据驱动的DnCNN模型从训练集中估计噪声信息，因而仅当待去噪图像噪声水平接近训练集噪声水准时，降噪效果才较理想，而FFDNet模型则将噪声水平图作为先验输入，因而可显著提升降噪效果。此外，所提算法在多数情况下皆可获得较高的PSNR，且相较于PID、NLM、BM3D、NNM、WNNM、DnCNN和FFDNet算法，所提算法PSNR在噪声水平为σn=10条件下分别平均提高0.44 dB、1.6 dB、0.33 dB、1.15 dB、0.22 dB、0.53 dB和0.43 dB，且随着噪声等级提高，PSNR改善更显著，此可归因于所提算法利用SSIM块匹配以提高相似图像块搜索准确度，且基于非凸伽马范数改善了秩函数的近似精度。由此可知，相比其他7 种算法，所提算法在不同噪声等级下均有较好的去噪性能。

对于噪声方差σn=50的House图像和噪声方差σn=100的Boats 图像，不同算法去噪结果分别如图4和图5 所示。

图4 House 图像去噪结果（σn=50）

图5 Boats 图像去噪结果（σn=100）

由图4 和图5 可知，NLM去噪图像存在大面积模糊现象，去噪效果较差，这是由于其搜索相似图像块中存在大量噪声，且仅利用加权平均相似图像块去噪的缘故；NNM利用矩阵低秩先验可有效避免图像大面积模糊现象，然而其均衡处理各个奇异值，导致去噪图像存在关键细节模糊和丢失等问题，比如图5(e)中船只的部分桅杆明显缺失；尽管WNNM可较有效地消除噪声，却存在图像细节丢失和纹理伪影等问题，此现象可归因于平均化过程中相似度度量收集了一些不相关的候选图像块；PID利用空域和频域联合处理及退火算法，有效解决去噪图像关键细节丢失问题，但仍存在细节模糊现象；BM3D则利用联合滤波方法，获得了较好的去噪效果，但由于其过于平滑图像，使图像信息丢失较多，进而导致去噪图像存在较强的伪影现象。再者，基于深度网络的DnCNN模型的降噪效果取决于训练集，仅当去噪图像噪声水平接近于训练集噪声水准时，才可获得较好的去噪效果，并且此模型无法较好地保持图像细节，且存在过度平滑现象；当噪声水平较低时，将噪声水平图作为先验信息的FFDNet模型可保留图像细节，但在光滑区域仍具有较多噪声；当噪声水平较高时，FFDNet模型可较有效地去除噪声，然而会平滑关键细节。此外，所提算法采用基于结构相似性指数的相似图像块搜索方法，并利用非凸伽马范数近乎无偏近似矩阵秩函数以克服上述缺点，进而改善算法的去噪性能。由图4(f)和图5(f)可知，所提算法去噪图像伪影现象较弱，且可较好地恢复边缘、纹理等关键细节特征。

综上所述，在不同等级高斯噪声条件下，所提算法的去噪性能比其他7 种算法改善显著，其不仅可有效避免去噪图像模糊及伪影现象，且可较好地恢复原始图像的关键细节信息。需要注意的是，尽管所提算法具有较好的去噪效果，然而由于结构相似性指数在某些区域不稳定，且依赖于输入参数的绝对值，因而基于结构相似性指数的相关算法稳健性较差[30]。针对此问题，后续研究将构建区域及输入参数不敏感的相似度量指标，以提升去噪算法的稳健性。

4.3 时间复杂度分析

实验选取标准图像库中的6 幅测试图像，并在上述计算平台评估不同算法的平均运行时间，测试结果如表2 所示。由表2 可知，非学习算法中的BM3D运行速度快于NLM、NNM、WNNM、PID和所提算法，其主要原因在于NLM、NNM、WNNM和所提算法采用图像块提取及相似图像块搜索操作较耗时，且NNM、WNNM和所提算法因为对相似图像块矩阵进行奇异值分解及多次迭代去噪操作，所以算法运行时间较长，而BM3D虽然包含图像块提取及相似图像块搜索操作，但代码优化后算法运行速度显著加快。其次，由表2 可知，基于深度网络的DnCNN、FFDNet模型运行速度快于其他非学习方法，且由于FFDNet网络深度比较浅，因此其运行时间小于DnCNN，然而，此二者需要额外的训练时间，且在训练样本较少时并不具有优势。再者，所提算法与NNM运行时间相近，但由于所提算法采用基于SSIM的相似图像块搜索方法，平均耗时比NNM长。需要注意的是，牺牲运算效率所换来的收益为不同噪声等级下所提算法较好的去噪性能，即不仅可较显著地抑制噪声，且可较好地避免伪影及细节模糊现象。此外，如前所述，所提算法基于SSIM搜素相似图像块，且需对相似图像块矩阵进行奇异值分解，因而计算复杂度相较于其他算法较高。针对此问题，在后续研究中，将基于图像亮度等先验信息缩小相似搜索区域，以加速搜索速度；基于相似图像块间强相关事实对相似图像块矩阵施加低秩等结构约束，以减少奇异值分解的数据量，从而降低所提算法的计算复杂度，进而提升其实时性。

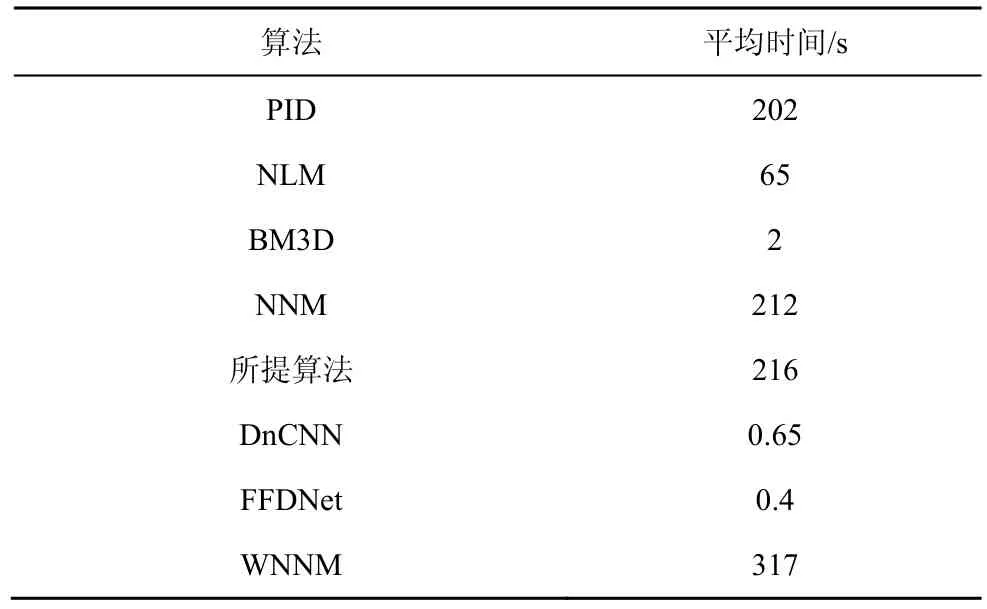
表2 不同算法平均运行时间对比

5 结束语

针对高斯噪声条件下去噪图像存在伪影及细节模糊问题，基于可近乎无偏近似秩函数的非凸伽马范数及低秩去噪模型，提出一种基于伽马范数最小化的图像去噪算法。首先基于综合亮度、对比度以及结构的SSIM构造相似图像块矩阵，可以避免传统方法相似图像块搜索不准确的缺点；然后利用非凸伽马范数构建低秩去噪模型，以解决传统秩函数近似方法估计精度较差的问题；最后基于奇异值分解求解所得非凸问题并重组去噪图像块以获得去噪图像。仿真结果表明，与现有主流PID、NLM、BM3D、NNM、WNNM、DnCNN、FFDNet等算法相比，所提算法虽因奇异值分解和多次迭代操作具有较高的计算复杂度，然而不同噪声等级下其具有比其他算法更好的去噪性能，即所提算法可较显著地消除高斯噪声，且可较好地避免伪影及细节模糊，恢复边缘及纹理等细节特征，因而可获得较高的图像重构精度。