基于时序关系的社交网络影响最大化算法研究
2020-11-03陈晶祁子怡
陈晶,祁子怡
(1.燕山大学信息科学与工程学院,河北 秦皇岛 066004;2.河北省虚拟技术与系统集成重点实验室,河北 秦皇岛 066004;3.河北省软件工程重点实验室,河北 秦皇岛 066004)
1 引言
随着互联网的快速发展,越来越多的人喜欢通过社交媒体传播他们的想法和信息来影响平台中的其他用户。如何使分享的信息快速传播并且影响范围最广,已成为社交网络分析领域的热点问题。针对此类问题,Richardson 等[1]首次提出了影响力最大化问题。目前广泛应用的基于静态社交网络的影响最大化问题是通过在社交网络中寻找k个用户作为种子节点,使信息在特定的传播模型下,通过种子节点在网络中尽可能多地影响其他用户。
目前,大多数研究通常将社交网络抽象为静态图,简化了影响最大化问题的研究,忽略了实际网络中节点间存在的时间关系特性,例如,人们之间相互的电话通信、邮件传送、交通网络和大脑神经网络等,进而造成了影响范围不准确的问题。在这些网络中,节点之间的联系并不会一直存在,而是只在某个时间段或者时间点存在联系,即节点之间的联系是动态的、具有时序性的。以时序信息传送为例,社交网络中的用户节点之间更加倾向于在特定的时间段内对某类主题信息进行交流和传播,因此,当研究信息在传播过程中具有重要作用的用户节点时,便可通过研究时序社交网络影响最大化问题来解决。
目前,针对时序网络的影响最大化研究很少,并且绝大多数研究集中在使用传统方法在时序网络上进行研究,即实验环境是具有时序特性的数据集,而研究方法是传统的。在此类问题中,由于时序社交网络中节点之间的时序性,节点间的联系状态是随着时间动态变化的,因此时序社交网络影响最大化问题面临如下挑战:1) 传统信息传播模型由于没有考虑网络的时序特性,故无法被应用于时序社交网络;2) 在种子节点选取过程中,节点影响范围的计算方式与传统方式不同。
为解决上述问题,本文针对网络的时序特性,以时序社交网络作为研究对象,将传统的信息传播模型时序化,并以此为基础设计了时序社交网络两阶段影响最大化(TIM,two-stage impact maximization)算法,该算法将网络的时序特性完全融入了种子节点的选取过程中,并分别通过时序启发阶段和时序贪心阶段进行研究。在时序启发阶段,结合网络的时序特性,定义了新的节点影响力估算方式,并选出估计值较大的节点作为备选节点;在时序贪心阶段,优化了节点间边际效益的计算方法,并从备选节点中精准地选取种子节点。该算法充分考虑了节点间的时序特性,时间复杂度低,影响范围与贪心(greedy)算法相近,可以高效地解决具有时序特性的网络影响最大化问题,并为相关问题的模型建立、种子节点选取以及如何降低时间复杂度提供了基础。本文的主要贡献如下。
1) 本文以时序社交网络为对象研究影响最大化问题,基于传统的加权级联传播模型,提出了新的计算节点间传播概率的方法,并以此为基础,进一步提出了改进的加权级联模型(IWCM,improved weighted cascade model),使信息可以在基于时序关系的社交网络图中进行传播。
2) 定义了一种新的节点影响力估算方式,基于该估算方式和IWCM 提出了两阶段时序社交网络影响最大化算法,有效地减少了程序的运行时间。
3) 验证了本文提出的TIM 算法可以高效地解决时序社交网络的影响最大化问题,且能在运行时间极短的情况下保证较高的影响范围。研究成果适用于中等规模对运行时间要求较高的时序社交网络。
2 相关工作
近年来,国内外研究者在影响最大化方面做了许多工作。Kempe 等[2]针对影响最大化问题,提出了贪心算法,并证明了其运算结果可以达到63%的近似最优,但仍旧存在时间复杂度较高、不适于大规模社交网络的问题。Leskovec 等[3]针对影响最大化问题的子模特性和单调特性对传统贪心算法进行优化,提出了比greedy 算法快约数百倍的CELF(cost-effective lazy-forward)算法。Goyal 等[4]通过优化CELF 算法,提出了CELF++,并通过实验证明其运算速度比CELF 快35%~55%。
上述算法均为贪心算法或改进的贪心算法,近年来,许多研究者对时间复杂度较低的启发式算法进行了研究。Chen 等[5]针对传统度估计算法的影响范围重叠问题,提出了DegreeDiscount 算法,首先选取度数最大的节点作为种子节点,然后将所选节点邻居的度数进行折扣,直到选择k个节点。Zhou等[6]首先使用PageRank 算法对节点影响力进行估算,并选择影响较大的节点作为备选节点,计算备选节点的组合碰撞概率,最后用遗传算法选择组合碰撞概率最大的k个节点作为种子节点。李阅志等[7]结合启发式算法提出了基于k-核过滤的影响最大化算法,经验证,该算法相较于现有的启发式算法具有更广的影响范围。
目前,越来越多的研究者开始研究影响最大化的延伸变形问题。仇丽青等[8]提出重叠社区的影响力最大化算法,该算法在运行时间方面最高能够提升约90%,可被应用于大型社交网络。Siyu 等[9]提出了多主题意识下的影响最大化问题,通过改进线性阈值模型,设计了一个跨社会网络的主题感知影响最大化模型,然后借助启发式算法选择种子节点。Li 等[10]考虑价格等因素,研究了产品在多条件限制的情况下,如何定价以实现收入最大化。赵玉芳等[11]考虑了社交网络中用户之间存在多种关系,且多种关系共同影响信息传播的情况,提出MR-RRset 算法,以解决多关系社交网络影响力最大化问题。
Kim 等[12]将影响最大化的研究对象转移到了动态图上,并设计了算法来处理动态图上的更新操作。Wang 等[13]在社交网络中定义了新颖的IM(influence maximization)查询,使用窗口滑动模型解决动态图上的实时影响最大化问题。Zhang 等[14]研究了网络中存在相互促进传播和相互抑制传播的不同关系时的影响力最大化问题。郭景峰等[15]对传统算法进行改进,使其适用于动态图的影响最大化问题,通过计算节点的删除或添加对当前采样集合的影响来重新计算种子节点集合。曹玖新等[16]设置了一个时间窗口,将节点间的联系看作一个动作。窗口随着时间向下滑动,此时新的动作进入窗口而旧的动作则退出,根据节点的进入和退出,判断是否需要对在上一个时间段所求出的窗口中的种子节点进行重新计算,以解决动态图中影响最大化问题。吴安彪等[17]以时序图为对象研究影响力最大化问题,对传统独立级联模型进行改进,并以此为基础提出了AIMT(advanced method for the influence maximization problem on temporal graph)和IMIT(improved method for the influence maximization problem on temporal graph)以解决时序图影响力最大化问题。魏磊[18]提出了一种基于节点度与网络最大系派相结合的度值衰减算法。Li 等[19]认为网络中不同节点间的传播概率是不同的,随着内容的变化有着不同的影响程度,并以此为基础研究了动态社交网络中影响最大化问题。
3 问题定义
3.1 基本定义
定义1基于时序关系的社交网络。给定网络GT(V,E,TE)表示基于时序关系的社交网络图,V表示节点的集合,E表示边的集合,其中|V|=n,|E|=m,TE表示网络中各节点间存在联系时刻的集合。
由于在社交网络的影响最大化问题中,经常使用图论的方法来表示社交网络,从而进一步分析影响最大化问题。本文给出了如图1 所示的静态图与基于时序关系的社交网络,并以此为例来说明静态图影响最大化问题和时序网络影响最大化问题在节点影响力计算方面的不同。相比于静态社交网络图G(边的权重表示节点的传播概率),时序社交网络图GT被赋予时间轴的概念,各节点只在特定的时间点存在联系,边上的权重表示两节点间存在联系的时刻,如图1(b)所示。相较于静态社交网络图1(a),图1(b)加入了时间权重的概念。如T(a,b)={3,6}表示节点a和节点b在3 和6 这2 个时刻存在联系。以真实的电子邮件网络为例,T(a,b)={3,6}表示用户a在3 和6 这2个时刻与用户b通过电子邮件进行了信息交流,其余时刻则不存在联系。因此,通过节点之间边的时间权重来体现时序社交网络的时序特性。现分别计算节点a在图1(a)和图1(b)中的影响范围,其计算过程如下。
为了便于计算,设图1(a)和图1(b)中各节点间传播概率相同,均为图1(a)中各边的权重值。在图1(a)中,节点a分别以0.1 和0.3 的概率去激活节点b和节点c。若此时节点c被激活,则节点c以0.1的概率去激活节点e,假设节点e此时被激活,则节点a成功将节点c和节点e激活,其影响范围为2。而在图1(b)中节点a分别以0.1 和0.3 的概率在3 和2 这2 个时刻去激活节点b和节点c。若节点c被激活,则节点c在时刻2 之后处于激活状态,由于节点c和节点e只在时刻1 存在联系,而在时刻1 节点c处于未激活状态,因此节点c不能将节点e激活,节点a只成功将节点c激活,其影响范围为1。
由此可见,若只是单纯地将基于静态图的影响力最大化算法应用在时序社交网络图上,则无法得到正确的结果,因此需要研究基于时序关系的社交网络影响最大化问题。
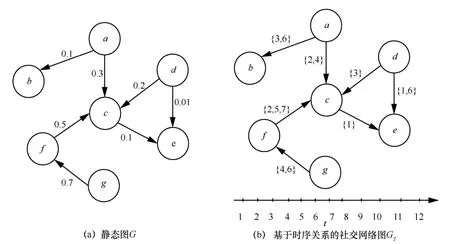
图1 静态图与时序社交网络
3.2 传播概率的计算
定义2传播概率。非活跃邻居节点v通过有向边(u,v)被其活跃父节点u激活成功的概率为传播概率,表示为Pu,v∈[0,1]。
在传统的影响力最大化算法研究中,计算节点间传播概率通常使用度估计的方法,即用该点入度的倒数来估计该点被上一级节点激活的概率,如式(1)所示。
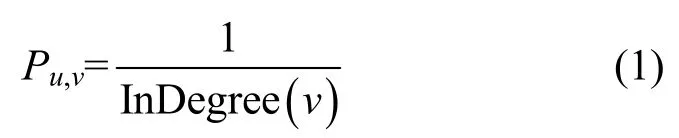
其中,InDegree(v)表示节点v的入度。
此方法在传统影响力最大化算法研究中已被很好地证实及应用。但是在基于时序关系的社交网络图中,该方法没有考虑到各节点间联系次数不同的问题,现针对此问题进行举例说明,如图2 所示。在静态图G中,由于节点c的入度为2,则节点c被节点a及节点d影响的概率均为。但是在图GT中,考虑连接次数因素时,可以发现节点c与节点a联系次数小于节点c与节点d的联系次数,而一个节点被联系的次数越多,意味着其被影响的概率越大,所以在图2(b)中节点c被节点a影响的概率应小于节点c被节点d影响的概率,其计算结果与图2(a)中不符,即用传统的度估计方法来计算时序社交网络图中节点影响概率是不准确的,因此,需要对传统计算方法进行改进。
在传统的度估计算法中,节点v被节点u激活的概率为边(u,v)占节点v所有入边的比重,即。而在基于时序社交网络的度估计算法中,由于时序关系的加入,每条边的权重不同,与两节点间联系次数|T(u,v)|相关,即联系次数越多的边,权重越大,且二者成正比关系,于是将边(u,v)的权重设定为|T(u,v)|,则边(u,v)占节点v所有入边的比重为,节点v被节点u激活的概率为
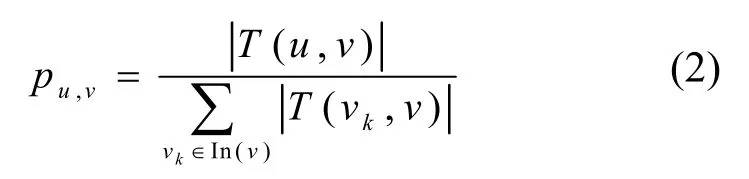
其中,|T(u,v)|表示节点u与节点v的联系次数,vk表示点v的所有入度节点,In(v)表示节点v的入度节点。

图2 传播概率计算示例
3.3 对加权级联模型的改进
3.3.1 传统的加权级联模型
传统的加权级联传播模型(WCM,weighted cascade model)为每条有向边(u,v)设置一个概率值且Pu,v∈[0,1],Pu,v表示节点u通过有向边(u,v)成功影响节点v的概率。该模型传播过程如下。在初始时刻t,种子节点u以概率Pu,v尝试激活它的非活跃邻居节点v。如果邻居节点v在t时刻有多个活跃父节点,则其父节点在t时刻依次对节点v进行尝试激活,如果邻居节点v被激活成功,则其将在t+1 时刻由非活跃状态转变为活跃,并以同样的方式去激活它的非活跃邻居节点。此过程一直循环,直到网络中没有新的节点被激活。
3.3.2 改进的加权级联模型
定义3节点活跃初始时间。节点v被其活跃父节点u成功激活的时刻为其活跃初始时间,表示为Actv,且Actv=min{t|(t∈T(u,v) &t≥Actu)}。
以图2(b)为例,设点d为种子节点(种子节点的初始活跃时间为0),若其成功激活节点c,则Actc=min{4,5}=4。
传统的影响最大化算法不需要考虑节点被激活的起始时间,而在基于时序的社交网络图中节点被成功激活的初始时间是需要被考虑的。因此,本文对传统加权级联模型进行改进,得到了一种新的基于时序社交网络图的传播模型——IWCM。
以图1(b)为例,设节点d为种子节点且成功将其邻居节点c激活,则节点c的初始活跃时间Actc=2,即节点c在时刻2 之后处于活跃状态,又由于节点c与节点e只在时刻1 时存在联系,此时节点c还处于未激活状态,因此节点c一定无法将节点e激活。
本节基于WCM 设计了IWCM,使信息可以在基于时序关系的社交网络图中进行传播。信息在时序社交网络图中通过IWCM 的传播过程描述如下。
1) 在最初始的网络中,设置所有节点的初始活跃时间Actv=−1,表示所有节点均处于非活跃状态。设置种子节点u的初始活跃时间Actu=0,表示种子节点在0 时刻处于活跃状态。此时种子节点u以一定的概率激活其邻居节点v,节点u有且仅有一次机会可以去尝试激活节点v。
2) 节点u在尝试激活节点v时,首先判断是否满足Actu≤max(T(u,v)),如果Actu>max(T(u,v)),则直接跳过该节点开始尝试激活下一个邻居节点;如果Actu≤max(T(u,v)),则节点u以概率激活节点v。
3) 无论节点u能否将节点v激活,节点u在以后的传播过程中都不会再激活节点v。
4) 如果节点v被成功激活,则记录其初始活跃时间Actv,其中Actv∈T(u,v),Actu≤Actv≤max(T(u,v))。
5) 在整个网络中,信息由新的活跃节点向非活跃邻居节点尝试传播,直到网络中没有新的节点被激活。
3.4 问题定义
基于上述问题的描述,本节对时序社交网络影响最大化问题进行定义及说明。首先对时序社交网络中节点影响力及边际收益的概念进行介绍。
定义4节点影响力。节点影响力是指在网络中可以被节点v成功激活的所有节点的集合,表示为σ(v)。
定义5边际收益。节点v的边际收益是指在种子集S中额外加入一个节点v所能带来的收益增量σv(S)。
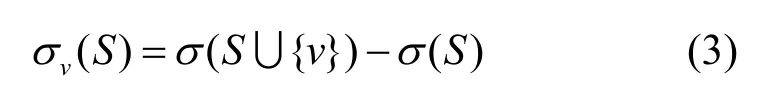
其中,σ(S)表示种子集合S的影响范围。
问题定义基于时序关系的社交网络影响最大化问题。给定时序社交网络图GT=(V,E,TE)以及特定的传播模型,在时序社交网络中找到一个节点集合S,其中集合S中含有节点个数|S|=k,使集合S的影响范围最广,集合S即为GT的种子节点集。
4 时序社交网络影响最大化算法
4.1 两阶段时序社交网络影响最大化算法
网络中度数较大的节点往往对其周边节点的影响力较强,但这只是局部最优的表现,并没有考虑到网络中所有节点的被影响情况,因此网络中度数大的节点一般具有较大的影响力,但并不一定具有最大的影响力。例如,在图3 中,节点a的度数最大,但是节点d拥有最大的影响范围。
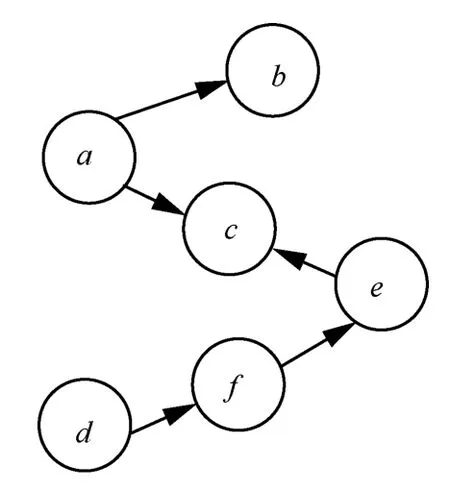
图3 影响范围示意
本文针对启发式算法这一特点,结合贪心算法可以精确计算出节点影响范围这一优点及时序社交网络影响最大化问题的时序特性,提出了TIM 算法,该算法的核心思想是将节点的选取过程分为2 个阶段。
1) 启发阶段及其时序化(时序启发阶段)。选取备选节点,考虑网络的时序特性,对所有节点进行影响力估算,选取估算值较大的节点作为备选节点。
在时序社交网络中,节点影响力不仅受到其出度的影响,还与两节点间的联系次数相关。如图4 所示,图中边的权重值表示两节点间的联系次数。由图4 可知,节点d与节点a的出度相同,均为2,根据度启发式算法可得,节点d与节点a的影响力大小相同。但是由于节点d与节点e、节点f的联系次数远远大于节点a与节点b、节点c的联系次数,即节点e、节点f被节点d尝试激活的次数大于节点b、节点c被节点a尝试激活的次数,因此节点f与节点e被激活概率应当大于节点c与节点b,即节点d的影响力应当大于节点a的影响力,这与度启发式算法得出的结果不同。
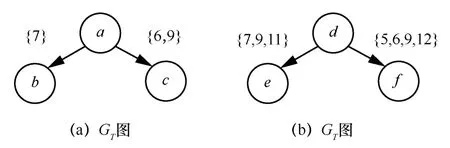
图4 节点影响力范围对比
针对此问题,为了使其适用于时序影响最大化问题,考虑节点间联系次数的因素,为节点影响力定义了新的估算方式,如式(4)所示。
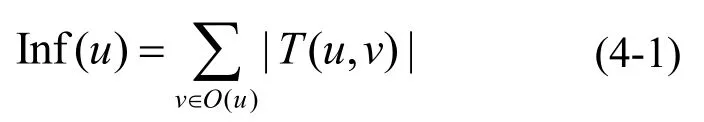
其中,Inf(u)表示节点u的影响范围,|T(u,v)|表示边(u,v)的联系次数,O(u)表示节点u的出度节点集合。
2) 贪心阶段及其时序化(时序贪心阶段)。从已过滤的备选节点中,选取最具影响力的节点。
解决传统影响最大化问题最有效的方法是每一步都选择当前最具影响力的节点加入种子集合中,直至找到k个节点。但此类算法由于要计算网络中所有节点的边际收益,从而使算法的运行时间过长,针对此问题,TIM 算法的贪心阶段将边际收益的计算对象由网络中所有节点缩减到了备选节点,并优化了节点间边际收益的计算方式,大大缩减了算法的运行时间。
优化后节点边际收益的计算过程为:首先读取每个节点可以激活的节点,并将可以被激活的节点放入与其父节点对应的列表中,如节点a可以激活节点b,则将节点b放入与节点a对应的列表σ(a)中,即σ(a)={b},同时计算出种子集可以激活的节点,并放入列表σ(S)中。如果想计算节点v的边际收益,则将σ(v)中节点与σ(S)中节点作对比,如果σ(v)中拥有3 个σ(S)中没有的节点,则节点v的边际收益为3。
针对时序社交网络的影响最大化算法,在计算节点影响力时,由于时序关系的加入,节点v能否被种子节点u激活不仅与激活概率Pu,v有关,还与初始活跃时间相关。当节点初始活跃时间Actu≤max(T(u,v))时,节点v才有可能被节点u激活。所以,在时序贪心阶段中,判断节点v能否被节点u激活,需满足2 个条件,即Actu≤max(T(u,v))和Pθ≤Pu,v,其中,Pθ为概率阈值。
时序贪心阶段的思想如下:该节点数法共执行k轮,每轮均从时序启发阶段选取的备选节点中选择边际收益最大的节点加入种子集合S中,直到|S|=k(其中,k为种子节点数)。
4.2 伪代码
用GT(V,E,TE)表示一个基于时序关系的社交网络,k为所需的种子节点数量,S为种子节点集合。算法1 给出了TIM 算法的执行过程。
算法1两阶段时序社交网络影响最大化算法
输入社交网络GT(V,E,TE),k
输出种子节点集合S
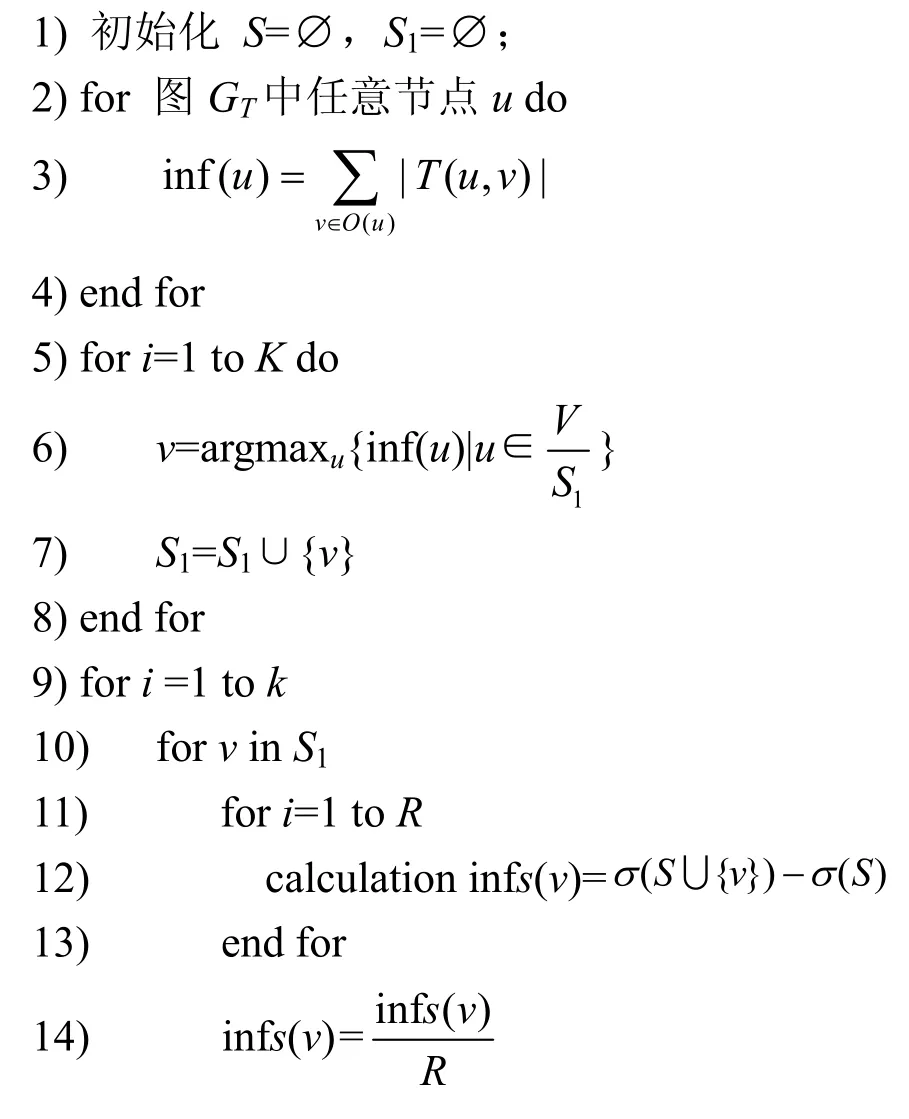
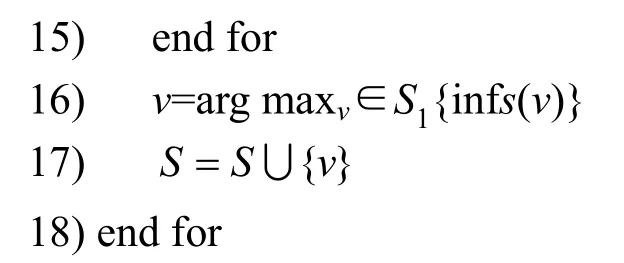
在算法1 中,步骤1)将备选种子集S1与种子集S初始化为空集;步骤2)~步骤4)估算所有节点的影响范围大小;步骤5)~步骤8)寻找影响范围估计值较大的前K(K为备选种子集的大小且k TIM 算法的时间复杂度分析过程如下。设网络GT(V,E,TE)的节点数为n,边数为m,种子集规模为k,网络中各节点间存在联系时刻的数量为t。算法1中,步骤2)~步骤4)计算所有节点Inf(u)值时产生的时间复杂度为O(n);步骤9)将计算节点影响力部分迭代k轮,故时间复杂度为O(k);步骤10)对所有备选非种子节点进行边际效应计算,计算完成后对所有备选非种子节点进行排序的运行时间为O(KlbK);步骤11)~步骤15)算法将节点影响范围的计算模拟了R次,故时间复杂度为O(R),综上所述,TIM 算法的时间复杂度为O(n+kRKlbK)。如果不采用TIM 算法将边际收益的计算对象由网络中所有节点缩减到备选节点,而直接选取贪心式算法计算所有节点的边际收益,则其时间复杂度为O(kRnlbn)。由于K≪n,即kRKlbK≪kRnlbn,因此TIM 算法的时间复杂度远远低于贪心算法。 本文选取了4 种不同规模的真实数据集作为输入数据,实现了在基于时序社交网络图中种子节点选取及种子影响力计算。 本文实验使用的数据集1(CollegeMsg)源于由私人消息组成的加州大学分校在线社交网络,边(u,v,t)表示用户u在时间t向用户v发送了一条私人消息[20]。数据集2(Email-Eu-core)为欧洲某大型研究机构的电子邮件数据,有向边(u,v,t)表示用户u在时刻t与用户v通过电子邮件进行了信息交流[21]。数据集3 源于Math Overflow 上的一个时间交互网络,边(u,v,t)表示用户u在时间t与用户v进行了信息交流[22]。数据集4 源于Ask Ubuntu 上的一个时间交互网络,边(u,v,t)表示用户u在时间t对用户v的答案发表了评论[21]。实验数据集参数如表1 所示。 表1 实验数据集参数 本文将基于时序社交网络图的影响力最大化问题分为两步解决。第一步为选取备选节点,通过改进的启发式算法实现节点的过滤,选出备选节点S1。第二步为选取种子节点,精确计算所有备选节点的影响范围,并选出影响力最大的前k个节点作为种子节点集。本文在实现了TIM 算法的同时,对基于时序社交网络的IMIT(improved method for the influence maximization problem on temporal graph)算法和基于覆盖阈值的影响力最大化(CTMD,coverage threshold maximum degree)算法以及一些经典算法进行复现,从算法的影响范围和运行时间2 个方面来对比分析各算法的优劣。 IMIT 算法是以时序社交网络为研究对象的影响最大化算法,该算法以贪心算法为基础,优化节点边际收益的计算方法,从而使其可以被应用于大规模时序社交网络[17]。 CTMD 算法是基于覆盖阈值的度最大启发式算法,利用改进的k-shell 算法计算节点影响力以选取初始种子节点,并计算两度以内节点的激活概率[23]。 IEIR(influence estimation influence ranking)算法是基于影响力估计和影响力排名的算法,是目前传统影响最大化算法中综合能力最好的算法[24]。 核覆盖算法(CCA,core covering algorithm)是基于网络层次结构和影响半径d的启发式算法,在实验中一般取d=1[25]。 DegreeDiscount 算法作为启发式算法的代表,选取度数最大的节点作为种子节点,然后将所选节点邻居的度数进行折扣,直到选择k个节点[5]。 greedy 算法为一个简单的贪心算法,用来做实验对比,计算出所有节点的影响力大小并进行排序,选取前k个节点作为种子节点[2]。 实验平台的操作系统为64 位的Windows 10,CPU 为英特尔 Core i5-8300H @ 2.30 GHz 四核,内存为8 GB,硬盘为128 GB,编程环境为Pycharm。 在种子节点选取阶段,IMIT 算法、CTMD 算法、IEIR 算法、CCA、DegreeDiscount 算法、greedy算法和两阶段时序社交网络影响最大化算法选取种子节点集合大小k分别为5、10、15、20、25、30、35、40、45 和50。 本文对相关算法在4 个不同的数据集上进行影响范围测试。影响范围influnece 是指在网络的初始阶段通过算法计算种子集,让种子集在网络中进行传播,最终影响到的节点个数。种子集的影响范围越广,说明算法的准确度越高。图5 给出了Email-Eu-core 数据集上的种子节点影响效果。从图5 中可以看到,greedy 算法影响范围最广,IMIT 算法和TIM 算法次之,其余算法中,属于启发式算法的DegreeDiscount 算法和CCA 的传播范围较好,IEIR算法和CTMD 算法的性能最差。 图5 Email-Eu-core 数据集上的种子节点影响效果 图6是CollegeMsg数据集上的种子节点影响效果。从图6 中可以看到,当k=50 时,greedy 算法和IMIT 算法信息传播范围最广,影响范围曲线几乎重合,且比TIM 算法、DegreeDiscount 算法、IEIR算法、CCA、CTMD 算法分别提高了16.8%、61.8%、81.1%、84.1%、90.4%。当k<20 时,greedy 算法与TIM 算法的影响效果折线几乎重合,其性能差异不大;当k>20 时,greedy 算法优于TIM 算法。CCA和CTMD 算法的性能最差。 图7 是Math Overflow 数据集上的种子节点影响效果。从图7 中可以看到,当k<40 时,greedy算法、TIM 算法与IMIT 算法的折线高度重合,影响范围几乎相同;当k>40 时,TIM 算法稍次于IMIT算法和greedy 算法。在其余算法中,IEIR 算法和DegreeDiscount 算法的影响范围较高,而CCA 和CTMD 算法的影响范围较低。 图6 CollegeMsg 数据集上的种子节点影响效果 图7 Math Overflow 数据集上的种子节点影响效果 图8是Ask Ubuntu数据集上的种子节点影响效果。从图8 中可以看到,TIM 算法和IMIT 算法的影响范围接近于拥有近似最优解的greedy 算法,且远远高于其余算法。当k<25 时,TIM 算法和IMIT算法的影响范围曲线与greedy 算法的曲线几乎重合,影响范围高度接近;当k>25 时,TIM 算法和IMIT 算法的影响范围略逊于greedy 算法。在其余4种算法中,DegreeDiscount 算法的影响范围最高,而CCA、CTMD 算法和IEIR 算法的影响范围较低。 本节实验在IWCM 传播模型下,分别对IMIT 算法、CTMD 算法、CCA、IEIR 算法、DegreeDiscount算法、greedy 算法和TIM 算法的运行时间进行了统计,所统计的时间为在4 种不同规模的数据集中,选择50 个种子节点的运行时间,如表2 所示。 图8 Ask Ubuntu 数据集上的种子节点影响效果 从表2 中可以看出,随着网络规模的增大,TIM算法、CTMD 算法、DegreeDiscount 算法、IEIR 算法、CCA、IMIT 算法的运行时间增幅较小,DegreeDiscount 算法的运行时间最短,TIM 算法次之,IMIT 算法、CTMD 算法、CCA 和IEIR 算法的运行时间较长,greedy 算法的运行时间最长,且随着网络规模的增大,greedy 算法的运行时间成指数级增长。 通过对实验结果的分析表明,IEIR 算法和CCA虽然是传统影响最大化算法中综合能力较好的算法,但由于时序影响最大化问题中时序关系的加入,导致算法的影响范围缩小,故不适用于时序社交网络的影响最大化问题的研究;CTMD 算法虽然是近两年较新的影响最大化算法,但同样没有考虑时序的因素,导致影响范围缩水;greedy 算法虽然影响范围最广,但运行时间也最长,由于现实生活中社交网络的规模一般较大,故该算法并不实用;DegreeDiscount 算法为启发式算法,运行时间最短,但影响范围也较小,达不到对算法影响范围的要求;IMIT 算法是以时序社交网络为研究对象的影响最大化算法,故能很好地贴合实际问题,同时该算法以贪心算法为基础,对节点边际收益的计算方法进行优化,相较于传统的贪心算法,其效率提高了300 倍。由于IMIT 算法是基于贪心算法的改进算法,因此其影响范围与贪心算法相近。与本文提出的TIM 算法相比,由于将节点影响力的计算范围由网络中所有节点缩减到了备选节点,导致节点影响范围的计算不够准确。由此可知,TIM 算法在影响范围略有降低的情况下,较大幅度地缩短了运行时间。以Ask Ubuntu 网络为例,当k=50 时,IMIT 算法的影响范围为423,而TIM 算法的影响范围为402,IMIT 算法的影响范围比TIM 算法提高了4.9%,但TIM 算法的运行时间比IMIT 算法缩短了一半,所以TIM 算法相比于IMIT 算法能以较小的影响范围为代价,换取更快的运行时间。 TIM 算法相较于IMIT 算法运行时间较短的原因如下。TIM 算法在时序启发阶段,节点影响力估算的时间复杂度为O(|V|)(V为网络中所有节点),而通过参考文献[17]可知,IMIT 算法的时间复杂度为O(ψ(v)|V|+|V|lb|V|),即TIM 算法时序启发阶段的运行时间要小于IMIT 算法。以Ask Ubuntu 网络为例,TIM 算法时序启发阶段的运行时间为0.093 s,而IMIT 算法为2.43 s,虽然TIM 算法还需要在时序贪心阶段对备选节点的影响范围进行精确计算,但备选节点数一般为100,相较于Ask Ubuntu 网络中75 555 的节点数,大规模地缩减了节点影响力的计算范围,该阶段的运行时间为0.52 s,所以TIM算法总体运行时间为0.093 s+0.52 s,即约为0.62 s,比IMIT 算法减少了近20%。IMIT 算法比TIM 算法影响范围广的原因如下。IMIT 算法对网络中所有节点的影响范围进行了精确计算,而TIM 算法只是对网络中所有节点进行了影响范围的估算,并选取估算值较大的前100 个节点进行影响范围的精确计算,而在影响力估算阶段由于计算的不准确性,可能出现影响范围较大节点的估计值较小,没有被选入备选节点中,从而损失了一部分的影响力。 表2 算法运行时间 综上所述,IMIT 算法更适用于大规模对影响范围要求较高的网络,而TIM 算法在小规模网络,例如Email-Eu-core 中,当k=50 时,备选节点的数量一般为100,而网络中总节点数为986,即在时序贪心阶段,节点影响力的计算范围仅缩减了89%,该比例较低,运行时间的优势体现不明显;在大规模网络,例如Ask Ubuntu 中,相较于网络中节点总数75 555,影响力的计算范围缩减了99.8%,虽然能节省大量的运行时间,但由于时序启发阶段节点影响力的估计范围较广,所以出现误差的概率较大,即计算影响力的准确度较差;而对于中等规模网络,例如Math Overflow 中,网络中总节点数为21 688,节点影响力的计算范围缩减了99.5%,该数量级适中,既可节约大量的时间成本,又能让影响力的误差值控制在较小的范围内,由表2 和图7可知,TIM 算法相较于IMIT 算法,在中等规模网络Ask Ubuntu 中,运行时间缩短了78.2%,而影响范围仅减少了2.25%,故TIM 算法更适于中等规模对运行时间要求较高的网络。 为解决以时序社交网络为研究对象的影响最大化问题,本文提出了TIM 算法。首先,通过改进度估计算法来计算节点间的传播概率;其次,对传统加权级联模型进行改进,使其可以应用于基于时序关系的社交网络上;最后,基于改进的加权级联模型提出了TIM 算法。在实际网络中,TIM 算法的影响范围远高于启发式类算法与传统影响最大化算法中综合能力最好的IEIR 算法和CCA,而与greedy 算法和IMIT 算法的影响范围相近;在运行时间方面,TIM 算法运行时间较快,略高于启发类算法,低于IMIT 算法、CTMD 算法、CCA 和IEIR算法,远低于greedy 算法。因此,TIM 算法在拥有较短运行时间的同时,保证了较广的影响范围,适用于时序社交网络的影响最大化问题。 在未来的工作中将会进行如下的深入研究:1)在基本时序社交网络影响最大化问题研究的基础上,考虑更多实际因素,如不同信息类型、成本、时间等因素对影响最大化问题的影响;2) 近年来有很多研究者利用社区结构来解决影响最大化问题并取得了很大的成果,未来可以尝试在时序社交网络图的基础上研究基于时序社交网络图的社区影响最大化。5 实验和评估
5.1 实验数据与参数设置

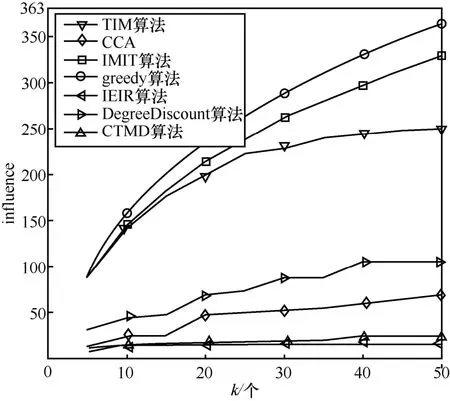
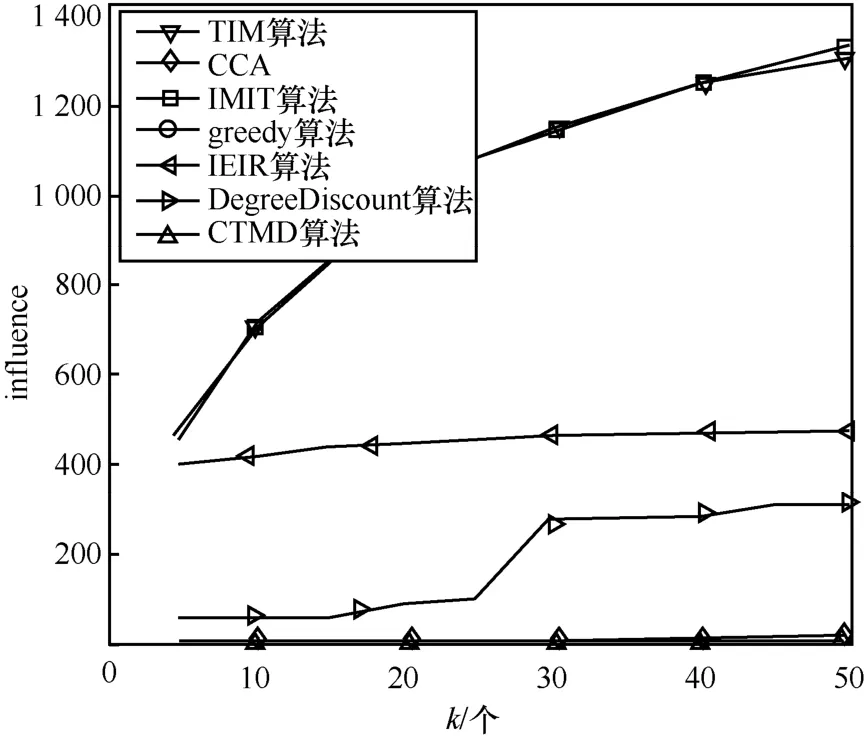
5.2 不同算法中种子节点影响力

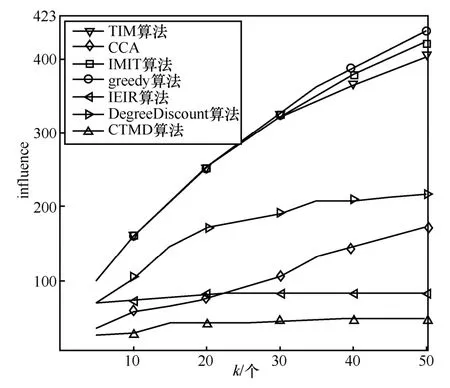
5.3 不同算法中种子节点选取时间
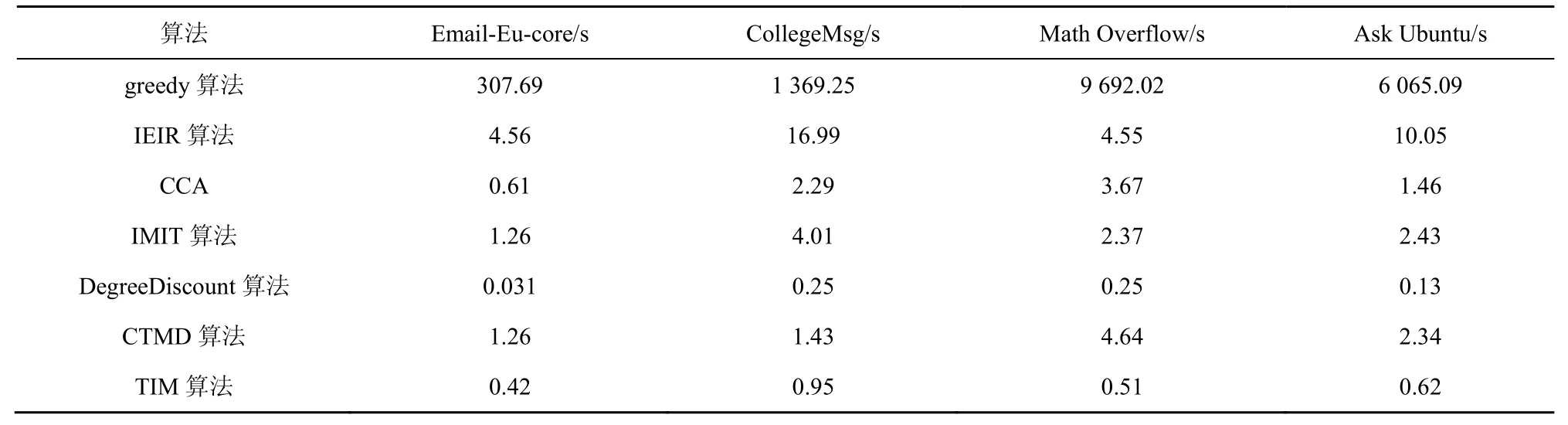
6 结束语
