基于DQN 的车载边缘网络任务分发卸载算法

赵海涛，张唐伟，陈跃，赵厚麟 ，朱洪波

（1.南京邮电大学教育部泛在网络健康服务系统工程研究中心，江苏 南京 210003；2.南京邮电大学江苏省无线通信重点实验室，江苏 南京 210003；3.南京邮电大学通信与信息工程学院，江苏 南京 210003）

1 引言

作为5G 移动通信代表性应用场景之一，车联网及自动驾驶已经成为热点研究领域，在未来将会经历前所未有的发展[1]。随着车联网等技术的快速发展及数据量的日益庞大，大量对计算资源高需求的车载应用任务随之出现，如自动驾驶、智能识别、实时路况等[2]。这些车载应用任务不仅需要大量的存储与计算资源，同时对于任务执行时延的要求非常严格，给现有车载设备的通信能力、计算能力带来了很大的挑战[3]。为了解决车辆终端与车载应用任务之间的矛盾，融合移动边缘计算（MEC,mobile edge computing）的协同通信技术被引入车联网中[4]。车辆终端携带的计算任务可以卸载到路边单元（RSU,road side unit）配置的MEC 服务器上，在车辆终端旁边就能够完成任务的计算及分析，有效缓解了车辆终端计算、存储资源不足的困境，减小了计算任务的处理时延与车辆终端能耗[5]。针对任务迁移和资源调度问题，国内外进行了大量相关研究。文献[6]对通信与计算融合技术的机遇与挑战做了大量的介绍，并针对“边缘智能”提出了具体的实施方案。然而，动态的车联网场景给MEC 技术的大规模应用带来了许多问题，车辆终端的高速移动及通信参数的变化导致计算任务卸载决策复杂化[7]。

目前车联网场景下计算任务卸载决策主要解决车载应用任务是否需要卸载及卸载多少的问题。卸载决策的主要优化目标有任务执行时延、能耗及时延与能耗的权衡等[8]。文献[9]提出了一种面向5G的边缘计算多用户卸载方案，将问题转换为多重背包问题，有效降低了任务执行时延。文献[10-12]基于各种数值优化算法，提出了一系列计算卸载决策及资源配置方案。基于马尔可夫决策过程理论（MDP,Markov decision process）的强化学习方法，如Q 学习算法、深度强化学习（DRL,deep reinforcement learning）方法如深度Q 网络（DQN,deep Q nework）也被研究人员用来解决卸载问题。文献[13]构建了马尔可夫决策过程函数，解决了车辆终端由于MEC 服务器服务范围不足而导致的服务中断问题，解决了单纯基于距离进行卸载服务的不足，但是该方法在卸载过程中没有对服务方的时延、能耗等成本进行合理的评估。文献[14]提出了一种基于DQN 的多用户单小区计算卸载与资源分配算法，联合优化任务执行时延与能耗的加权和，实现了任务总成本的下降。与其他方法明显不同的是，DQN 可以在没有任何先验信息的前提下与环境进行交互，从中学习并调整卸载策略以达到最佳的长期回报[15-16]，这对于动态时变的车联网环境来说尤其重要。

上述方法都没有针对不同车辆终端进行任务优先级划分，从而不能实现处理程序的优化。同时这些方法需要实时准确的信道状态消息，算法复杂度高、迭代步骤长，难以满足时延敏感型的车联网通信系统。针对以上研究中存在的问题，本文通过引入移动边缘计算，根据车辆终端任务属性的不同进行优先级划分，使车辆终端携带的计算任务能够直接在边缘节点进行处理；在车辆终端，基于DQN研究了计算速率最优的任务卸载策略，在信道条件时变的环境中能够根据过去的经验实现卸载策略的自我更新，从而有效降低任务执行时延、提高车联网车辆终端用户的使用体验。

2 系统模型

本文选取车辆终端、RSU 与其连接的MEC 服务器所构成的网络通信模型。由于车辆终端的快速移动，车联网络拓扑架构会产生动态变化。为了满足时延要求，车辆终端将其携带的计算任务迁移至RSU 连接的MEC 服务器中。这产生了2 个问题，具体如下。

1) 卸载决策的制定问题。由于计算任务的类型、信道增益均不相同，如果将计算任务统一卸载到MEC 服务器，在信道增益很差的情况下会造成非常严重的传输时延问题，同时车辆终端计算资源也得不到充分利用，导致计算资源浪费。因此本文根据车辆终端信道实时状态制定卸载决策，将部分车辆终端的计算任务卸载至边缘侧服务器，从而降低计算任务处理时延、提高计算资源利用率。

2) 计算资源分配问题。系统会根据业务类型分配优先级，但是相同类型业务由于其属性的不同，也可能具有不同的优先级需求，因此，必须在计算资源分配之前根据计算任务属性的不同进行预处理，否则相同的卸载决策会导致MEC 服务器不能合理分配计算资源，影响用户使用体验。

车联网环境下的计算任务卸载模型架构如图1所示。在该模型架构中，受限于较弱的计算能力，部分车辆终端会将自身携带的计算任务通过无线网络卸载到RSU 连接的MEC 服务器进行处理。首先，车辆终端会将自身携带的计算任务信息如最大可容忍时延、数据量大小、计算复杂度等上传至RSU。RSU 通过计算得到计算任务优先级，然后根据MEC 服务器的计算任务调度算法决定将哪些车辆终端的计算任务卸载至服务器。车辆终端随后接受RSU 的调度信息，开始卸载或执行计算任务。假设在计算任务执行过程中，一旦执行时间超过其最大容忍时延，就判定当前计算任务执行失败，并将当前计算任务执行时间设置为最大值。

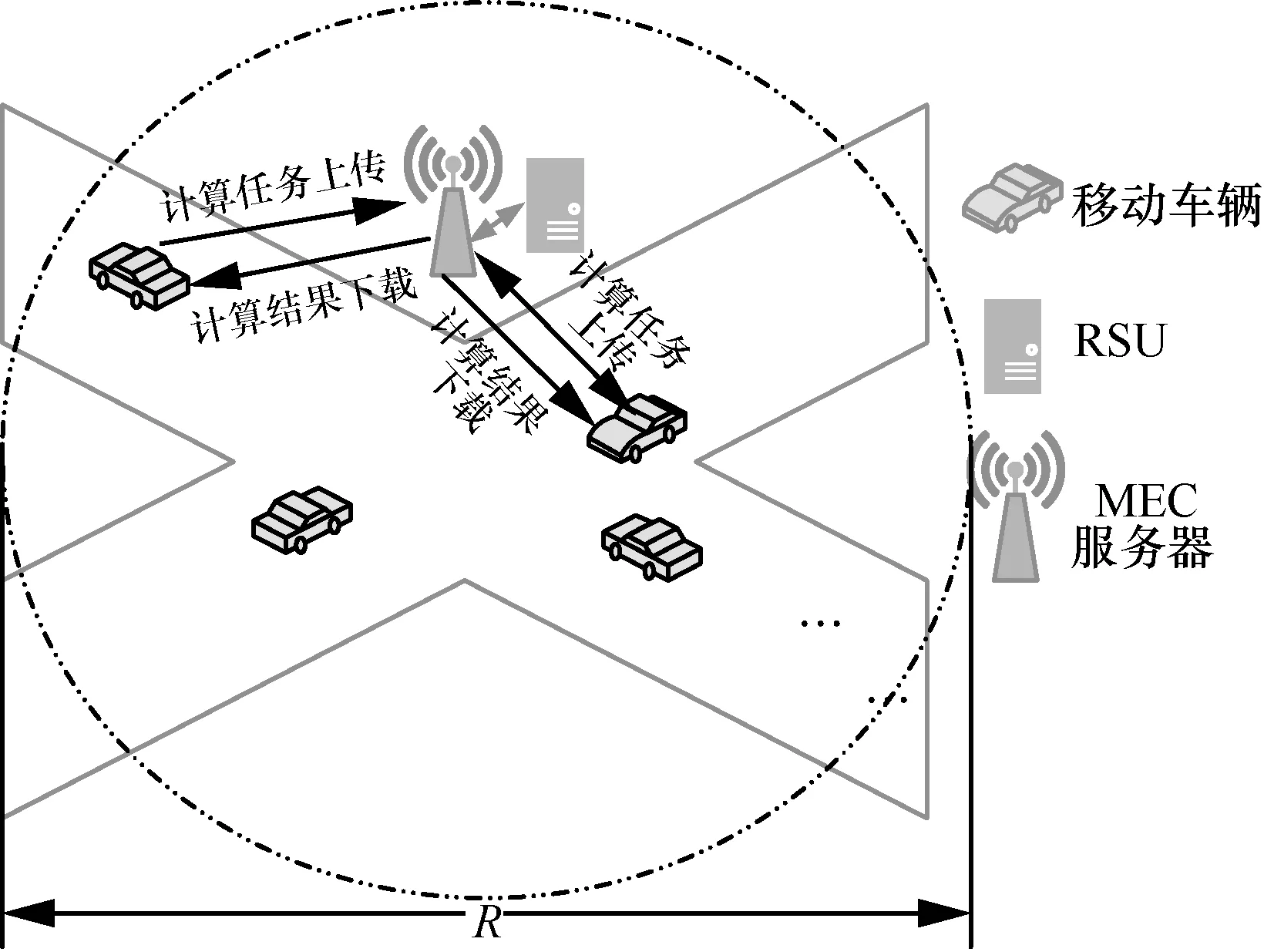
图1 计算任务卸载模型架构

本文假设RSU 覆盖范围内有K个车辆终端，车辆终端携带的计算任务表示为Ck=(Vk,Dk,Γk,Pk)，其中，Dk表示计算任务的数据大小，单位为bit；Vk表示计算任务计算复杂度，单位为round/bit；Γk表示计算任务最大可容忍时延，单位为ms；Pk表示计算任务的优先级，由RSU计算后得出。假设计算任务无论是在车辆终端执行还是卸载到MEC 服务器执行，以上参数均保持不变。RSU 覆盖范围内的所有车辆终端的计算任务表示为M={M1,M2,…,Mk}，其中k∈K。

3 车载边缘网络计算任务分发卸载方案

3.1 计算任务优先级划分

车辆终端将携带的计算任务卸载到MEC 服务器时，由于计算任务类型的不同导致所需要的计算资源也不同。层次分析法（AHP,analytic hierarrchy process）指将与决策总是有关的元素分解成目标层、准则层、方案层等层次，并在此基础之上进行定性和定量分析的决策方法，是一个多标准决策/多属性决策模型，非常适用于权重分配的计算任务调度应用场景[17]。本文通过AHP 算法可以给容忍时延小、计算复杂度高的计算任务分配相对高一些的权重系数，为MEC 服务器的计算资源调度过程提供更合理的依据，提高车辆终端计算任务的卸载执行成功率。

当确定计算任务的权重系数时，本文主要考虑计算任务的计算复杂度、数据总量和最大容忍时延这3 个评价因素，其中，计算复杂度的重要程度最高，数据总量次之，最大容忍时延最低。本文将计算任务目标层的因素进行两两比较，构造出评价因素判断矩阵A=(aij)3×3，以及目标层相对于准则层的判断矩阵B1,B2,…,B3=(aij)K×K。其中，

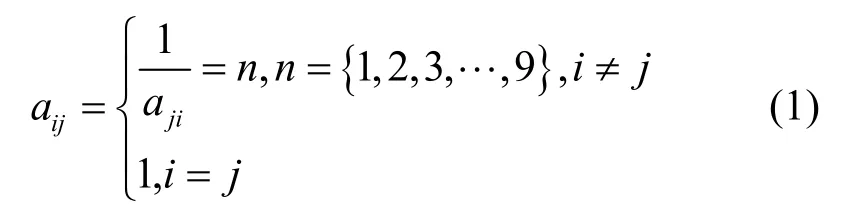
根据方根法求得判断矩阵Bk对应的权重向量元素，如式(2)所示。

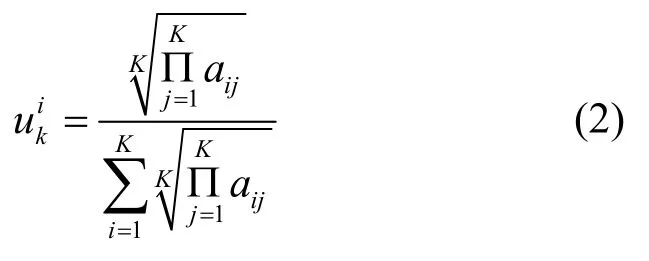
其中，k表示第k个终端车辆，i表示第k个终端车辆所携带任务的第i个评价因素，可以得到所有车辆终端计算任务的权重矢量矩阵为

根据同样的方法求得评价因素判断矩阵A的权重向量Δ=[Δ1,Δ2,Δ3]，其权重元素为

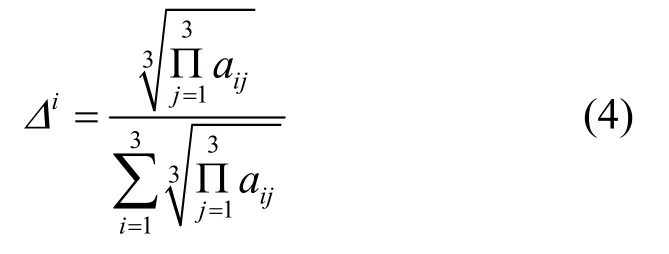
权重元素通过一致性检验后，得到所有计算任务的权重向量W，其中每一个元素分别代表对应车辆终端计算任务的权重，如式(5)所示。

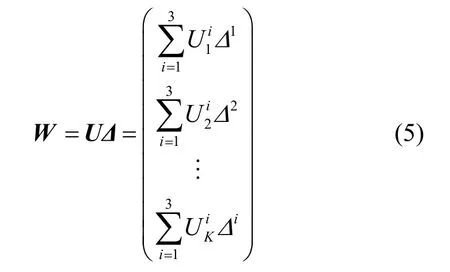
3.2 卸载决策制定问题的建模

车辆终端携带的计算任务分为车辆终端计算模式和卸载计算模式。车辆终端用于执行计算任务的总能耗Econstraint为额定值，当前计算任务执行能耗Ecurrent表示为

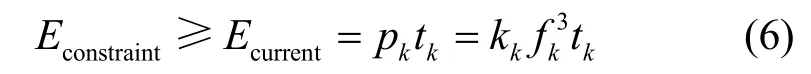
其中，pk为车辆终端发射功率，kk为能量效率系数，fk为车辆终端处理器频率，tk为计算任务传输时间或车辆终端执行时间。

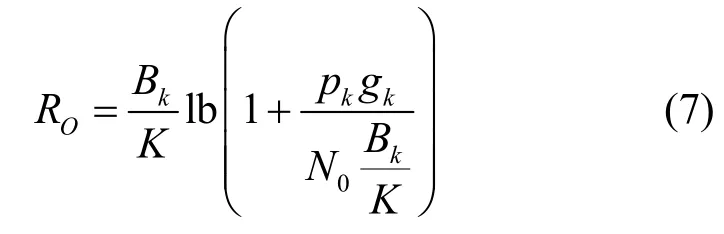
其中，Bk为当前车辆终端传输带宽，其中最大传输带宽为BHz，N0为信道传输噪声。基于LTE-V2X（long term evolution-vehicle to X）技术，本文假设无线信道增益gk、车辆终端发射功率pk及传输带宽Bk在对应的时间段内均是时变的，并且基于分布式方式下的SPS（semi persistent scheduling）资源分配算法[19]对RSU 覆盖范围下的车辆终端进行统一控制。本文以最大化计算任务处理速率为优化目标，以车辆终端能耗与传输带宽为约束，在求得计算任务处理速率最大加权和之后，可求得对应的计算任务最小执行时延。同时，基于式(5)得出的计算任务权重wk，对于优先级别更高的计算任务可以分配更多的计算资源，使其执行时间小于计算任务最大容忍时延，保证计算任务卸载过程成功进行。本文的优化目标为

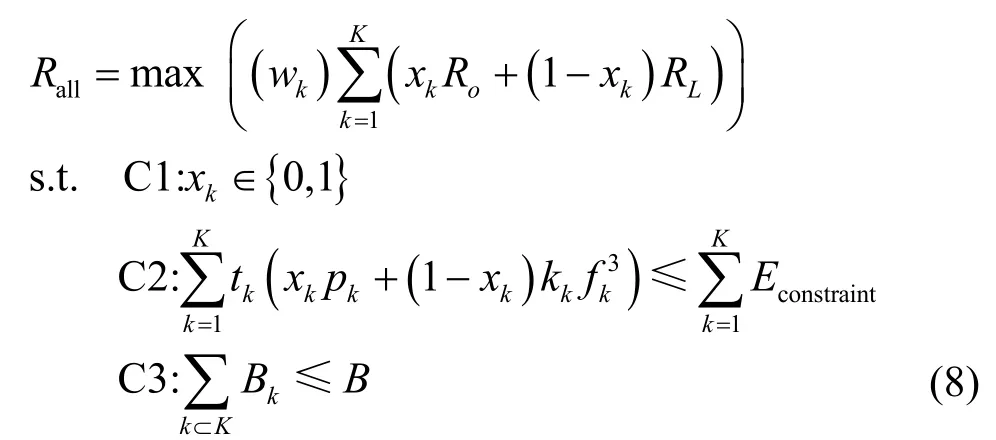
其中，xk表示为卸载决策向量元素，xk=0 表示车辆终端计算模式，xk=1 表示卸载计算模式；约束条件C2 和C3 分别表示计算任务执行能耗和车辆终端传输带宽不能超过额定值。

通过求出卸载决策向量的最优值可以求解式(8)所示优化问题。然而该问题是一个非凸问题，随着车辆终端数量及计算任务大小的增加，该问题的计算复杂度也会迅速增加。

3.3 AHP-DQN 任务分发卸载算法

面对上述挑战，传统的数值优化方法效率较低。本文提出了一种AHP-DQN 任务分发卸载算法，其核心思想是将Q 网络作为策略评判标准，通过Q网络遍历当前状态下的各种动作与环境进行实时交互，其动作、状态值、奖励值存放于回访记忆单元通过Q 学习算法经历多个迭代过程来反复训练Q网络，最后得到最佳卸载策略。与文献[14]算法不同的是，本文算法通过引入层次分析法对车辆终端计算任务进行预处理，提高MEC 服务器对计算资源的合理分配能力。同时重新定义了Q 网络中的奖励函数，以加权后的计算任务处理速率和为优化目标，减小算法迭代过程中的计算复杂度，加快算法收敛速度。本文的卸载决策算法致力于设计一个卸载策略函数，当MEC 服务器收到车辆终端的计算任务信息并得出计算任务对应的权重时，能够根据当前车辆终端的无线信道增益情况，快速调整深度学习网络参数θt，并生成计算任务卸载策略，策略函数可以表示为π:g→x。该策略函数的产生可以分为两步，具体如下。

1) 卸载决策动作的产生。当MEC 服务器收到车辆终端当前的信道增益信息后，深度学习网络根据当前观测到的状态st得到卸载动作向量Xt=[x1,x2,…,xK]，并根据式(7)生成奖励值rt。同时本文的动作状态函数Q(st,xt,θt)由深度学习网络确定，深度学习网络激活函数为ReLu 函数，网络输出函数为Sigmoid 函数，其对应卸载动作的概率值。

2)卸载决策动作的更新。根据式(9)实现动作状态函数的更新。

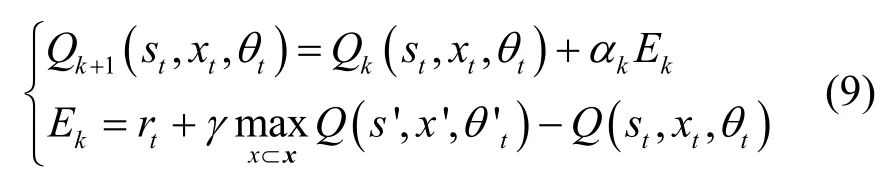
其中，αk与γ分别为学习速率与折扣因子，s'为第k次迭代过程中执行动作xt后的状态观测值，x'为状态s′下奖励值最大的动作，Ek为迭代过程中的累积奖励值。对于第k次迭代过程而言，通过最小化式(10)目标函数，可以更新网络参数θ，从而实现卸载决策动作的更新。

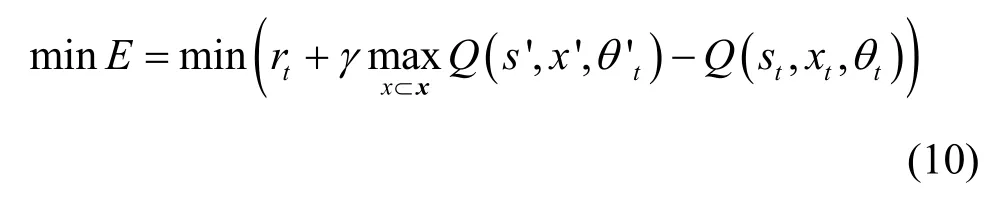
重复上述2 个步骤得到t时刻最佳状态对后，将该状态−动作对(gt,)放入经验池，作为新的训练样本。当经验池容量足够后，新生成的状态−动作对会代替旧的数据样本。深度学习网络反复学习最佳状态对(gt,)，并随着时间的推移生成更好的卸载决策输出。在存储空间有限的约束下，DNN 仅从最新生成的数据样本中进行学习，这种闭环强化学习机制会不断改善其卸载策略，直到收敛。本文算法伪代码如算法1 所示。

算法1AHP-DQN 计算任务分发卸载算法

输入计算任务的计算复杂度Vk、数据总量Dk及最大容忍时延Γk。根据式(1)～式(5)得到每个计算任务的优先级Pk，即计算任务的计算资源分配权重

输出车辆终端携带任务的最终卸载决策X=[x1,x2,…,xK]

4 仿真结果与分析

本节通过Python 编程语言对本文算法进行仿真以评估算法性能。本文仿真场景为IEEE 802.11p 标准规定下的车联网场景，仿真实验参数根据文献[20]及移动边缘计算白皮书相关约束进行假设。在车联网场景下，每个RSU 的覆盖范围为1 000 m，车辆终端速度假设为40 km/h，每个车辆终端计算能力为108round/s，车载车辆终端计算功率为3 W，发射功率为0.3 W。携带的计算任务数据（以kbit 为单位）服从[300,500]的均匀分布，计算任务复杂度（以兆轮为单位）服从[9 000,11 000]的均匀分布。下面将本文算法分别与全部车辆终端计算、Q 学习算法、DQN[14]进行比较。

本文算法收敛过程如图2 所示。纵轴分别表示训练过程中所有车辆终端的归一化计算速率及损失函数值。根据经验风险最小化的知识，收敛概率与网络复杂度负相关，结合应用场景的实际维度情况，本文选择了两层DNN 结构，同时在时延要求较高的车载边缘网络中并不注重未来的潜在回报，因此本文设置了一个较小的折扣因子γ。在样本不多的初期采用较高的学习速率αk，随着经验池样本增加，逐渐减小αk，避免损失函数过于震荡。在设计Q函数与奖励值时，一方面尽量使收敛过程中Q的均值为0，另一方面使奖励值的正反馈稍大些，保证初期奖励值的负反馈过程中能够采取人工干预提升正回报，加速收敛过程。从图2 可以看出，在车辆终端数目为10 的情况下，本文算法经过50 次迭代后，DQN 已经逐渐收敛到最优解。与Q 学习算法的收敛结果相比较，本文算法得到的优化目标具有更好的效果。从图2 还可以看出，尽管设置了较大的经验回放池尺度，由于贪婪概率ε的存在，收敛曲线存在些许波动，但不影响算法总体的收敛性。

图2 3 种算法的收敛过程

图3 中，在车辆终端数目为10 的情况下，将本文算法与全部车辆终端计算、Q 学习算法[14]进行比较。从图3 可以看到，随着计算任务复杂度的增加，3 种算法的计算任务执行成功率都在下降。当计算任务复杂度最高时，全部车辆终端计算的计算任务执行成功率只有24%，Q 学习算法的执行成功率由81%下降到了64%。与之相对应的是，本文算法的执行成功率保持了一个相对稳定的状态。与Q 学习算法一样，本文算法只对能耗及传输带宽做了相应的约束，但是随着计算任务复杂度的上升，计算任务的差异度变大，基于AHP 算法对计算任务做的预处理能够使MEC 服务器更加合理地调度计算资源，从而提高计算任务卸载执行成功率。

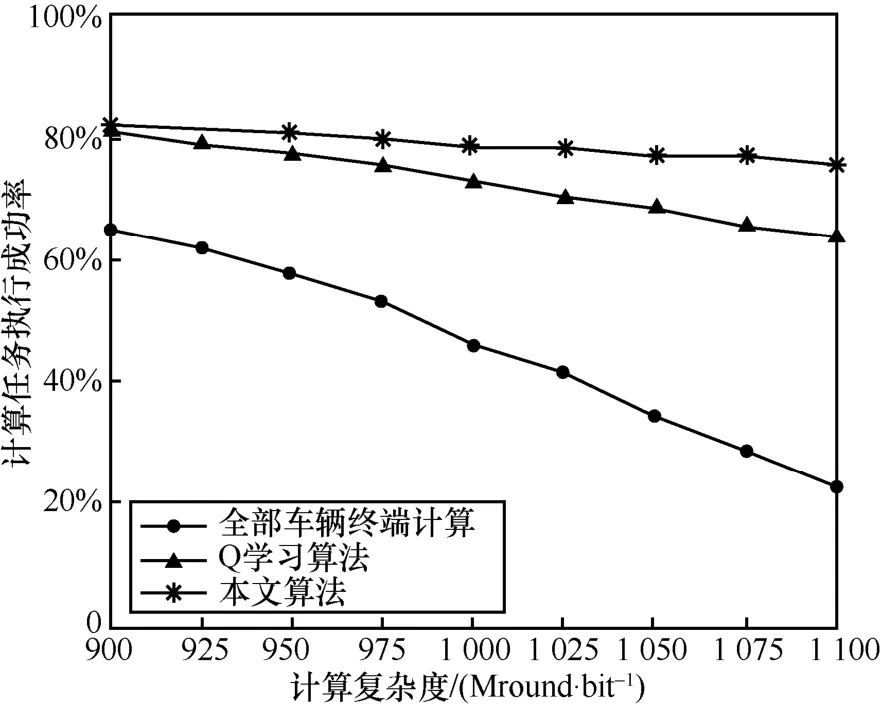
图3 计算任务执行成功率与计算复杂度的关系

在计算任务复杂度不变的情况下，将本文算法与全部车辆终端计算、Q 学习算法、DQN 进行比较，如图4 所示。从图4 可以看到，随着车辆终端数的增加，计算任务量变大，计算任务执行时延都随之上升。当车辆终端数目小于10 时，本文算法与Q学习算法、DQN 的执行时延几乎没有不同。当车辆终端数目超过10 时，本文算法的计算任务平均执行时延相比全部车辆终端计算的时延减少了95 ms，相比Q 学习算法减少了24 ms，相比于DQN 有些许提升。随着计算任务数目的增加，相比全部车辆终端计算与Q 学习算法，本文算法的卸载方案能够根据信道实际情况进行学习，从而做出更合适的卸载决策，使计算任务执行时延更小。但是在仿真实验中，仅改变车辆终端数目，车辆终端计算任务的计算复杂度、数据量大小等属性保持不变，基于AHP算法对计算任务做出的预处理产生的效果有限，因此本文算法与Q 学习算法的效果提升有限。

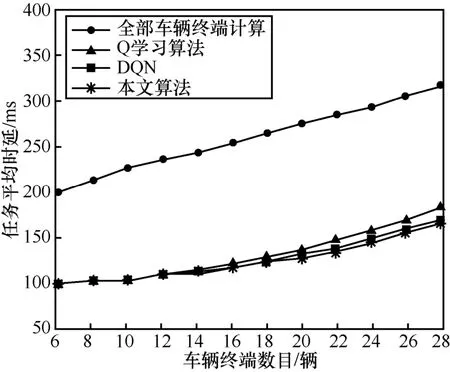
图4 任务平均时延与车辆终端数目的关系

在车辆终端数目为10 的情况下，随着一半的车辆终端计算任务计算复杂度的增加，4 种算法的计算任务平均执行时延都在增加，如图5 所示。从图5 中可以看出，在计算任务复杂度最高时，本文算法的计算任务执行时延与全部车辆终端计算相比减少了219 ms，与Q 学习算法相比减少了64 ms，与DQN 相比减少了24 ms。比较图4 与图5 可以看出，在计算任务差异度越大的应用场景中，本文算法优势越明显。随着计算复杂度的上升，不同车辆终端的计算任务差异度越大，MEC 服务器计算资源的分配权重也随之变化。与Q 学习算法和DQN 不同的是，本文算法对所有车辆终端的计算任务做了自适应优先级预处理，给优先级更高的计算任务分配了更多的计算资源，使计算任务执行成功概率更高，从而提高卸载决策正确率，有效减小了计算任务执行时延。

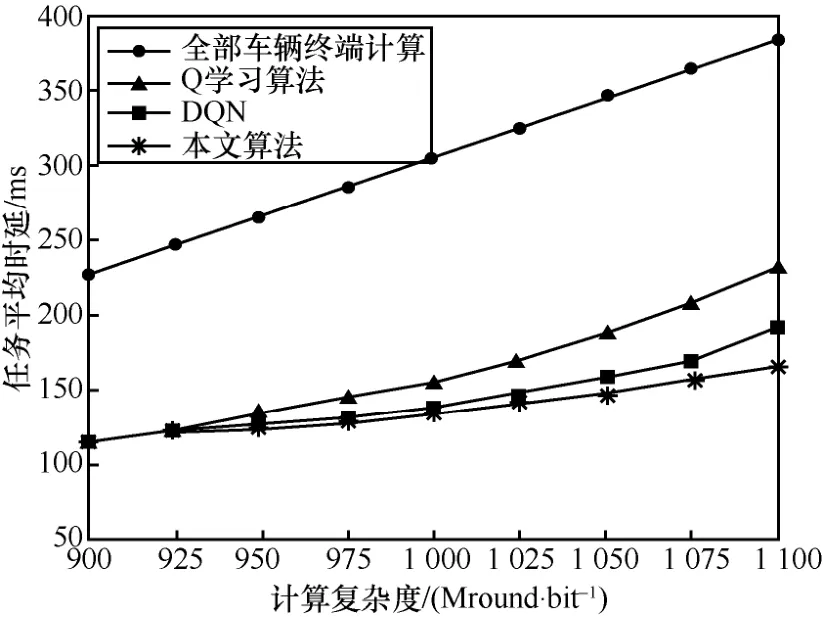
图5 任务平均时延与计算任务复杂度的关系

5 结束语

面向车联网环境中车辆终端受最大容忍时延及最大能耗约束的情况，本文提出了一种基于深度Q 网络的计算任务分发卸载算法。车辆终端首先根据自身计算任务大小、计算复杂度及最大容忍时延等因素对计算任务优先级进行合理划分，并根据车辆终端实时信道增益进行自主卸载决策部署，以找到最优策略。通过对该算法的大量仿真分析及数值验证，本文提出的AHP-DQN 任务分发卸载算法在不同的系统参数下都具有较好的性能。今后的研究将会考虑对DQN 的训练算法及神经网络结构进行持续优化改进，同时对无线电干扰等复杂环境因素也会加以考虑。