基于能效最大的无线供电反向散射网络资源分配算法

徐勇军，谷博文，陈前斌，林金朝

（1.重庆邮电大学通信与信息工程学院，重庆 400065；2.重庆邮电大学−伦敦布鲁内尔大学交叉创新研究院，重庆 400065）

1 引言

随着物联网（IoT,Internet of things）技术的发展，海量设备节点通过无线的方式接入物联网中，从而导致整个通信系统的能耗增大。与此同时，设备有限的电池容量与人们日益增长的速率需求之间的矛盾日益严峻[1-3]，因此，如何在提高传输速率的同时最大程度地减小网络能耗是一个亟待解决的关键问题。

近年来，反向散射通信技术[4]和无线供电通信技术[5]的出现，使解决上述问题变成了可能。具体来说，反向散射通信允许反向散射节点调制和反射入射的射频波来传输数据，而节点本身不对信号进行处理[4]。同时反向散射节点作为超低功耗的微型设备，可以灵活地进行大规模的部署，有效提升了网络覆盖范围。无线供电通信技术则缓解了物联网节点设备过于依赖电池供给的问题[5]，从而使基于无线供电的反向散射通信成为学术界和工业界的研究热点。

资源分配是无线通信网络中的关键技术，即通过动态调整发射功率来提高用户的服务质量[6]。目前，对反向散射网络资源分配问题的研究已取得一些有价值的成果[7-15]。针对典型的反向散射网络，文献[7]通过联合优化传输时间和传输功率使传输速率最大化。文献[8]通过优化反射系数、时间分配以及功率分配，来最大化系统吞吐量。为提高频谱利用率，文献[9-10]基于全双工方式接入的反向散射网络，提出了联合优化传输时间、反射系数以及发射功率的资源分配算法，使系统吞吐量最大化。基于非正交多址接入的反向散射网络，文献[11]考虑了能量收集门限和信干噪比的约束，通过联合优化反射时间和反射系数使系统吞吐量达到最大化。但上述工作都是针对传统的反向散射通信网络，没有对能量利用做进一步的讨论。基于无线供电反向散射网络，文献[12]提出了反向散射和收集−转发2 种模式协作的资源分配方案来最大化传输速率。在相同网络场景下，文献[13]研究了能量收集、反向散射和无线传输的最佳时间分配使吞吐量达到最大化。针对无线供电的认知反向散射网络，文献[14]通过研究反向散射、能量收集与能量传输的资源分配算法来最大化系统吞吐量。然而，上述工作主要集中在传输速率的提升，没有综合考虑系统能耗的影响。为了平衡传输速率与系统能量消耗的关系，文献[15]基于无线供电反向散射网络，提出了能效最大化的资源分配算法，该算法优化了反射系数、传输时间和发射功率，但并没有考虑对收集能量分配的联合优化，而这对系统传输速率的提高有着重要的意义。此外，部分研究采用的交替迭代算法和分块协调算法无法求得全局最优解。

为了提高设备运行周期和系统传输效率，求得多参量全局最优解，本文研究了基于无线供电的多载波反向散射通信网络资源分配算法，主要贡献如下。

1) 建立了一个多载波无线供电反向散射通信系统模型。为了提高传输效率，将信号传输分为反向散射通信阶段和数据传输阶段。考虑了发射功率约束和能量收集约束，建立了一个多变量多约束的能效最大化资源分配问题。

2) 由于上述模型含分式目标函数和多变量耦合关系，很难直接获得解析解。首先，利用Dinkelbach方法将目标函数转化为非分式问题，并分解为多个单变量求解的子问题；其次，根据信号传输阶段解耦的子问题，基于注水算法获得该阶段的最优功率分配因子；再次，将该最优值代入原问题；最后，利用变量替换方法，将关于其他优化变量的资源分配问题转换为凸优化问题，并利用拉格朗日对偶原理求得各变量的全局最优解。

3) 仿真结果表明，所提算法具有较好的收敛性能。与传统纯反向散射通信算法、纯能量收集算法相比，所提算法具有更好的能效。

2 系统模型

本文考虑由一个反向散射设备、一个接收器和一个基站组成的无线供电反向散射网络，如图1 所示。反向散射设备具有无线能量收集模块和反射电路。考虑系统传输时隙Tslot，该时隙包括数据反射阶段Tbc和数据传输阶段Ttd。在数据反射阶段，基站将信号发送到反向散射设备，反向散射设备在反射信号给接收器的同时收集能量。在数据传输阶段，将一部分收集能量用于反向散射设备向接收器的数据传输，以提高传输质量。假设总带宽被划分为K个正交子载波，每个子载波带宽为单位带宽。定义子载波集合为∀k∈ K={1,2,…,K}，每个子载波服从平坦衰落[16]。假设基站与接收器距离较远，因此可以忽略它们之间的干扰。系统参数如表1 所示。

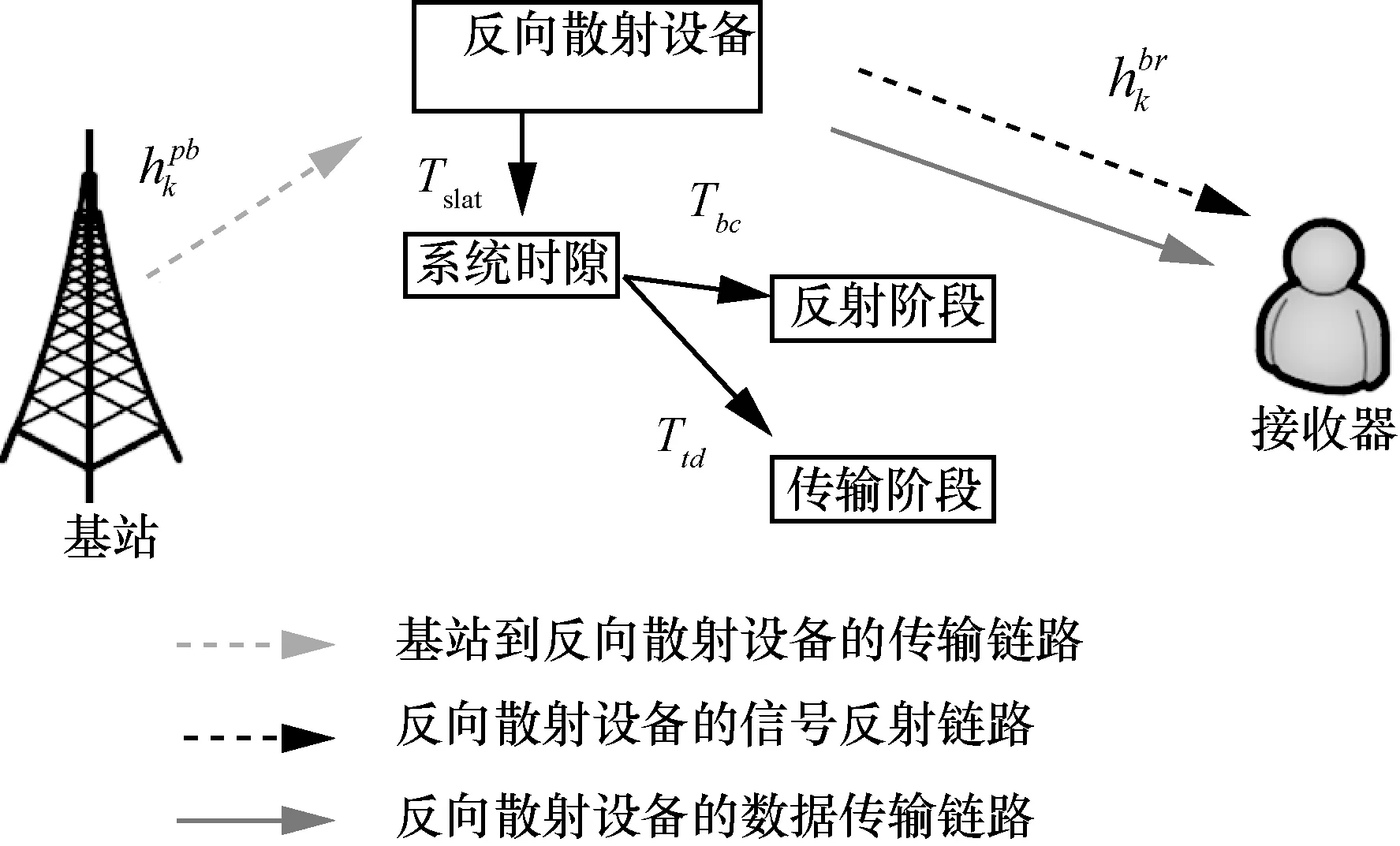
图1 无线供电反向散射网络模型

表1 系统参数

在Tbc期间，基站通过子载波k向反向散射设备发送信号sk(t)，满足E[|sk(t)2|]=1，则反向散射设备接收到信号y(t)可表示为

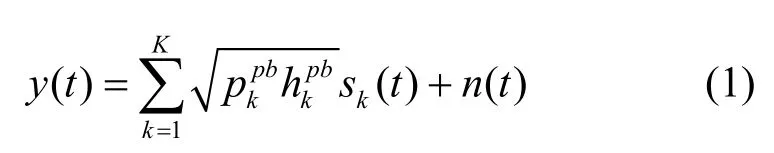
其中，n(t)表示接收端的噪声，满足n(t)～CN(0,σ2)。

本文的目标是在基站发射功率门限和收集能量约束下，通过对功率分配、时间分配、反射系数、能量收集分配系数的联合优化来使反向散射网络的能效最大。定义，则能效最大化模型建立为

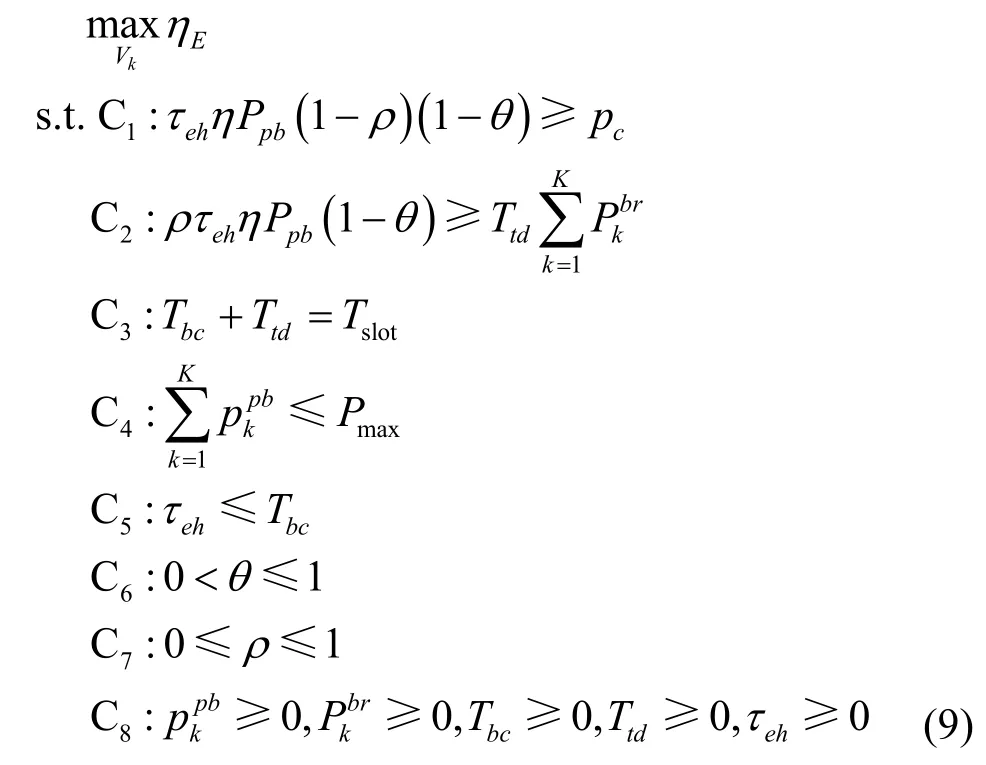
其中，约束条件 C1和 C2表示关于最小能量收集的约束，前者用于保障设备所收集的能量不小于其消耗的能量，后者用于限制数据传输的能量不超过分配的收集能量；约束条件 C3表示系统传输的时间；约束条件C4表示限制每个子载波上的最大发射功率；约束条件C5表示能量收集的时间不超过数据反向散射的时间。由于式(9)为多变量耦合形式的分式规划问题，该问题为非凸问题，难以求得解析解。

3 最优资源分配算法

基于Dinkelbach 方法[16]，目标函数式(9)可以转换为如下形式。

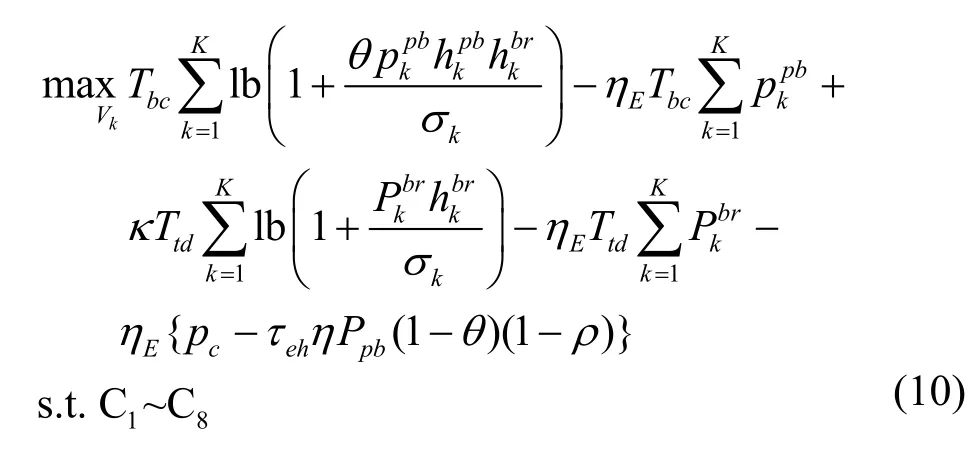
由式(10)可得，Ttd期间的数据传输功率仅受约束条件 C2约束。因此，本节首先求出最优的数据传输功率的闭式解，然后将其代入式(10)中，获得最优能量分配系数ρ*的闭式解，最后通过适当的变量替换将非凸问题转换为凸问题，即可求得全局最优解。

3.1 求解最优传输功率

由于反向散射设备处的可用发射功率受分配收集能量的限制，根据式(10)分解出关于数据传输功率的子问题为

3.2 求解最优能量分配系数ρ

讨论命题1 的目的是提出一个闭式表达式(17)，以得到最优收集能量分配系数。当满足条件时，最优能量分配系数ρ*会随着能量收集时间τeh增大而减小，也就是说收集的能量将更多（甚至全部）地用于电路消耗而不是数据传输。如果维持一个较高的能量分配系数，便意味着反向散射设备在Tbc期间将减少能量收集的时间τeh，系统则需要在有限的时间收集足够的能量，即减少信号反射系数θ或增加基站的信号功率Ppb，但上述措施将进一步降低系统能效；当条件成立时，最优能量分配系数ρ*会随着能量收集时间τeh的增大而增大，假设电池容量充足，则。从而，将为Ttd阶段数据传输提供更多的能量，与此同时，如果来自基站的信号功率Ppb增加，能量分配系数也会增加，这也说明了更高能效的可能性。

3.3 求解其他参数最优值

由于能量分配系数ρ≥ 0，则可用的信号反射系数θ必须满足

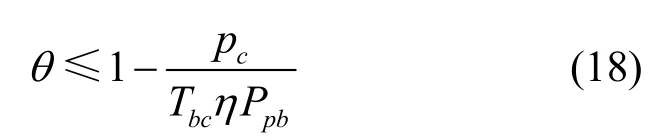
将式(15)和式(17)代入式(10)中，优化问题就可以转变为以下关于时间分配和功率分配的优化问题，即

其中，α和βk是约束条件 C4与 C10的非负拉格朗日乘子。式(21)可以重新描述为

基于梯度下降方法，令t表示迭代次数，ΔT、Δp、Δα和Δβ表示相应的迭代步长，则可以对优化变量和拉格朗日乘子通过式(29)～式(33)进行更新。

3.4 计算复杂度分析

本文考虑多载波反向散射网络，提出了联合优化发射功率、时间分配、能量分配系数、信号反射系数的能效最大化的资源分配算法。首先，由于系统为K个子载波确定最优的分配方案，此时需要 O(K)次运算。假设外层拉格朗日迭代次数和内层优化求解迭代次数分别为T和I，根据式(34)～式(38)，迭代更新需要 O(TK)次运算，内层迭代次数I是迭代次数O(IK)的多项式函数。所以算法的总计算复杂度为O(TIK3)。通过选择合适的步长，对偶算法可以很快取得收敛。

4 仿真结果与分析

本节针对多载波无线供电反向散射网络对所提算法进行仿真分析。为验证所提算法的能效性，本文分别对比了传统纯反向散射算法[7]和传统纯能量收集算法[12]。假设基站到反向散射设备的最大距离和反向散射设备到接收器的最大距离分别为6.2 m和1 m[4]。基站的天线增益和反向散射设备的天线增益设置为6 dBi[4]。信道模型为，其中dk是发射端和接收端之间的距离，χ=3是路径损耗指数[15]，其他仿真参数如表2 所示。

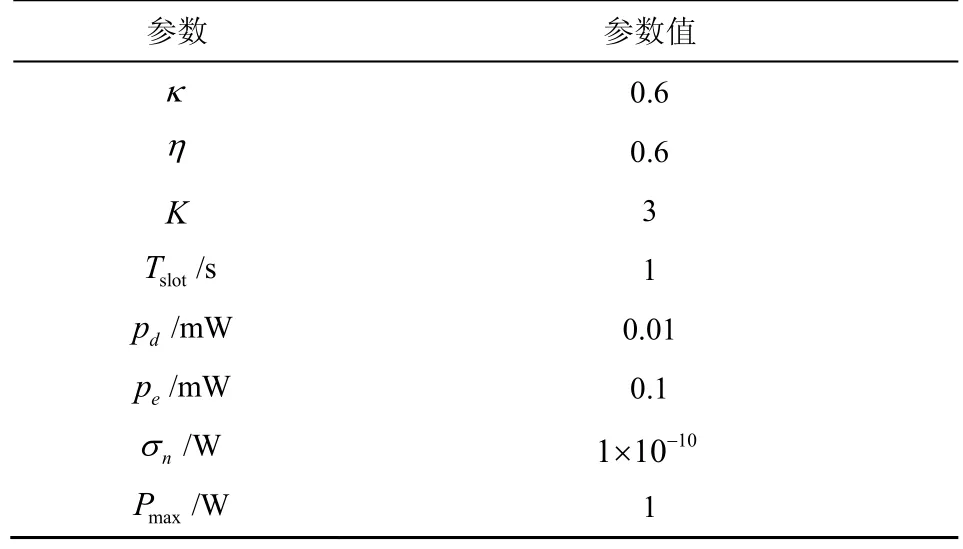
表2 仿真参数

图2 给出了不同子载波个数下系统的能效收敛性能。从图2 可以看出，系统能效随着迭代次数的增加逐渐增加，在经过大约5 次迭代之后趋于收敛，具有较好的收敛性。同时随着子载波个数的增加，系统能效也随之增加，其原因在于随着子载波个数的增加，可利用的频谱资源增加。同时正交频分多址接入技术可消除不同载波间的干扰。因此，传输效率增加，从而能效增加。

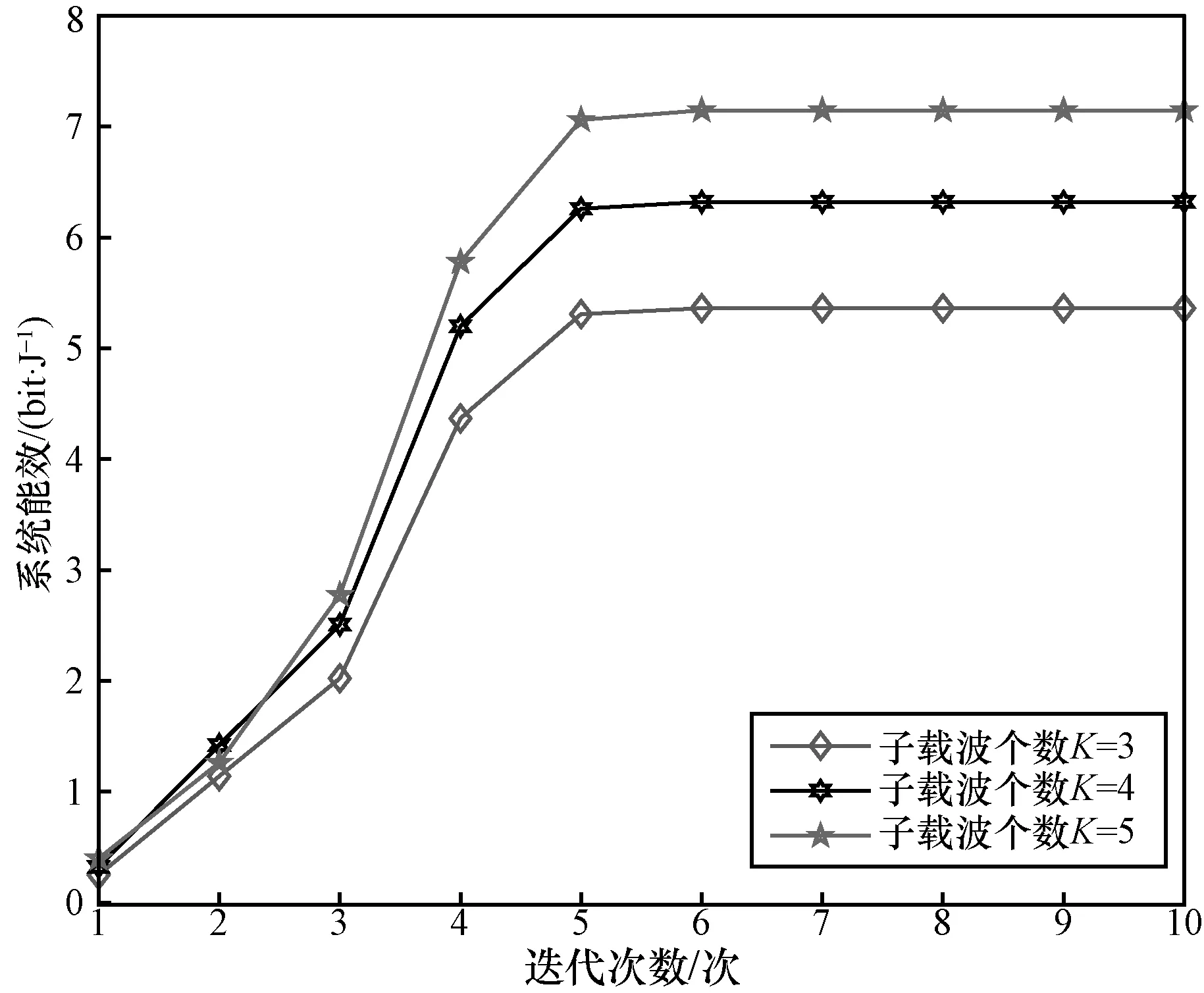
图2 不同子载波个数下系统的能效收敛性能

图3 给出了不同信道状态下系统的能效收敛性能。从图3 可以看出，所提算法在经过较少次的迭代后趋于收敛。同时基站到反向散射设备距离越近，系统具有的能效越好，其原因在于发送端与接收端距离越小，传输信道的增益越高，从而数据传输速率越高。

图3 不同信道状态下系统的能效收敛性能

图4 给出了不同算法下系统能效与基站功率门限的关系。从图4 可以看出，随着基站功率门限的不断增大，3 种算法的能效也随之增大且逐一收敛。具体来讲，传统纯反向散射算法的能效最低，而本文所提算法具有最好的能效。其原因在于传统纯反向散射算法仅是将收集的能量用来补偿设备消耗，这使得能量利用率低下。此外，传统纯能量收集算法则需要在传输数据前，消耗一定的时间来收集能量，这影响了数据传输的效率。而本文所提算法的传输模式为复合传输模式，兼具反向散射以及能量收集模式的优点。

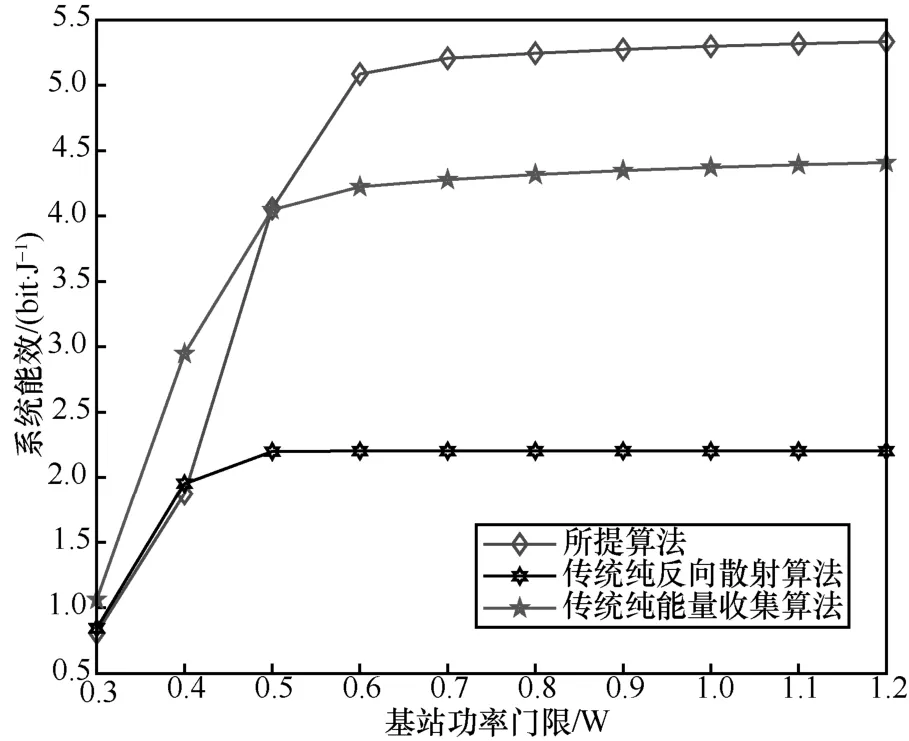
图4 不同算法下系统能效与基站功率门限的关系

图5 给出了不同算法下系统能效的收敛性能。由图5 可知，随着迭代次数的增加，3 种算法的能效也在逐渐增加。此外，所提算法在收敛后具有最大的能效，而传统纯反向散射算法的能效最小。其原因在于，传统纯能量收集算法需要一个专用的时隙来收集能量，然后才能进行数据传输。此外，传统纯反向散射算法则无法进一步利用收集能量进行数据传输。而本文所提算法结合了二者的优势，充分利用了时间和无线能量来使提升系统能效。

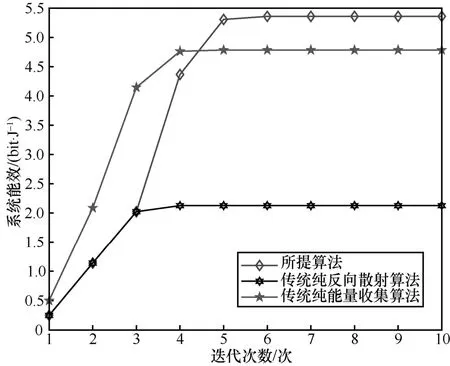
图5 不同算法下系统能效的收敛性能

5 结束语

基于多载波无线供电反向散射网络，在满足发射功率门限和能量因果关系的条件下，本文对基站发射功率、反射系数、能量分配系数、传输时间分配问题进行联合优化，以追求网络能效最大化；针对提出优化问题建立相应模型，利用Dinkelbach 理论和变量替换方法，将原始问题转化为易于求解的凸优化问题；基于拉格朗日对偶原理求得全局最优解，并对算法进行了复杂度分析。仿真验证了所提算法具有较好的收敛性和能效。

附录 命题1 的证明

证明由于式(21)是凸函数，因此不可能在变量ρ取值范围内直接获得目标函数的单调趋势，因此在做出判断之前，需先求得其驻点ρ0，则有

另一方面，根据约束条件C1，可得ρ满足。

结合上述2 个条件，即可证明所提命题。

证毕。