扩散应力诱导的锂离子电池失效机理研究进展

王亚楠, 李华, 王正坤, 厉青峰, 练晨, 何鑫

扩散应力诱导的锂离子电池失效机理研究进展

王亚楠1,2,3, 李华1,2,3, 王正坤1, 厉青峰1, 练晨1, 何鑫1

(山东大学1. 机械工程学院; 2. 高效洁净机械制造教育部重点实验室; 3. 机械工程国家级实验教学示范中心, 济南 250061)

在锂离子电池的充放电过程中, 由锂离子扩散过程产生的浓度梯度和活性材料锂化膨胀产生的变形会导致扩散应力。过大的扩散应力会造成活性颗粒的破裂、活性颗粒之间的分离、活性层的断裂以及活性层与集流体的分层等多种力学失效形式, 并最终导致电池出现容量衰减、阻抗上升和寿命缩短等一系列失效现象。因此扩散应力及其诱导的锂离子电池失效机理已经成为锂离子电池研究领域的热点之一, 具有重要的理论研究意义和实际应用价值。本文尝试从活性颗粒、活性电极、半电池、电池单元和电池单体等不同尺度, 综述近年来与扩散应力诱导的锂离子电池失效机理相关的研究进展, 介绍各尺度下扩散应力的产生机制和研究手段, 分析扩散应力对电池力学和电化学性能的影响规律, 梳理和总结扩散应力的影响因素, 最后对该领域今后的研究方向与发展趋势进行了展望。

锂离子电池; 扩散应力; 失效机理; 多物理场耦合模型; 综述

与镍氢电池、镍镉电池和铅酸电池等二次储能电池类型相比, 锂离子电池具有工作电压高、能量密度大、循环寿命长、无记忆效应等优点, 已成为目前纯电动和混合动力等新能源汽车的首选电池类型。为了满足对新能源汽车动力性、经济性、安全性、续航里程、充电速度等方面越来越高的要求, 锂离子电池需要具有更高的容量、更大的功率、更低的价格、更长的寿命以及更好的安全性。但是, 商业化的锂离子电池在生产、储存和使用过程中经常出现各种类型的失效现象, 如容量衰减、寿命缩短、内阻增加、电压降低、倍率下降、自放电、析锂、产气、内短路、热失控等, 而电池单体的失效会影响电池模组乃至整个电池系统的电化学性能、一致性、可靠性和寿命, 甚至导致严重的安全问题。因此, 对锂离子电池失效机理的研究具有重要意义。

造成锂离子电池失效的原因很多, 并且有些非常复杂[1]。而在锂离子电池的各种失效现象中, 有相当一部分是由电池内部产生的扩散诱导应力(简称扩散应力)直接或间接导致的[2]。过大的扩散应力会造成活性颗粒的开裂、破碎甚至粉化, 活性颗粒之间的分离, 活性层的开裂和断裂, 活性层与集流体的分层剥离等多种失效形式, 从而导致电池出现容量衰减、内阻增加、倍率下降和寿命缩短等多种失效现象[3]。由此可见, 扩散应力及其诱导的电化学性能的衰退对锂离子电池的性能和寿命具有非常重要的影响。由扩散应力诱导的锂离子电池的失效机理也是目前锂离子电池研究领域的热点之一, 国内外相关学者对该问题进行了大量的理论、实验和数值仿真等方面的研究工作。本文尝试对近年来与扩散应力诱导的锂离子电池失效机理有关的研究进行介绍、归纳和总结, 为今后更加全面和深入的分析与讨论提供参考。

1 不同尺度下的扩散应力

锂离子电池的扩散应力源于活性材料在锂离子嵌入和脱出过程中产生的体积变化, 可以在活性颗粒、活性电极、半电池、电池单元和电池单体等不同尺度下产生(图1)。一方面, 在锂离子电池的充放电循环过程中, 大量的锂离子嵌入/脱出活性材料, 使活性材料产生晶体结构和晶格大小的变化以及晶相和非晶相之间的相变, 从而导致活性材料发生膨胀或收缩, 在相邻颗粒、集流体和外部封装等结构的约束作用下产生扩散应力; 另一方面, 锂离子在活性材料内部的扩散过程会导致浓度梯度, 不同位置的不均匀锂浓度会造成活性材料的不均匀变形, 从而也在相应位置产生扩散应力。不同尺度下产生的扩散应力会诱导对应尺度下的失效形式, 并导致电池整体性能降低和寿命缩短。

在活性颗粒和活性电极等微观和介观尺度下, 目前还很难直接进行扩散应力的测量, 研究手段通常以理论建模和数值仿真为主; 而在半电池、电池单元和电池单体等介观和宏观尺度下, 已经有比较成熟的测量手段, 可以采用实验或数值仿真技术进行扩散应力的研究。实验测量一般是对制备的半电池或全电池进行电化学循环, 并采用力学量传感器或光学测试仪器测量电极或电池的应力/力或应变/变形, 同时监测电池的容量、阻抗和循环寿命等性能的变化。数值仿真所采用的模型以有限元模型为主, 主要类型有电化学–机械耦合模型、电化学–热–机械耦合模型和其他多物理场耦合模型等。通常需要先根据电化学模型计算出待求解区域的锂浓度分布, 然后根据锂浓度和电极材料的最大可嵌锂浓度max计算不同位置处的局部荷电状态(State of Charge, SOC)

图1 锂离子电池在不同尺度上产生的扩散应力

(a) Active particle[4]; (b) Active electrode[5]; (c) Half cell[6]; (d) Cell unit[7]; (e) Cell[8]

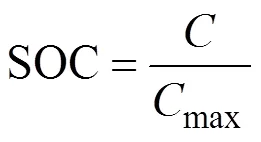
然后可以通过以下几种方法获取活性物质在充放电时的体积变化(即应变):

1)根据电极材料的体积变化率(Volume change ratio)随SOC的变化关系得到不同位置的体积变化。如石墨材料的体积变化率与SOC的关系如图2所示[9]。

2)根据电极材料的锂化膨胀系数计算出不同位置的体积变化[10]:

3)根据电极材料的偏摩尔体积计算不同位置的体积变化[11]:

最后根据体积变化和电极材料的力学参数(如弹性模量和泊松比)求解不同位置的扩散应力。通过研究扩散应力与电化学性能的相互作用关系, 寻找改善电池性能的方法, 如容量、寿命、阻抗、倍率等; 或通过研究扩散应力的影响因素, 寻找降低应力水平的措施。

图2 石墨材料的体积变化率与SOC的关系[9]

2 活性颗粒尺度下的扩散应力

当锂离子嵌入活性颗粒时, 会与活性材料及在此等候的电子发生电化学反应, 导致活性材料锂化膨胀, 同时在活性颗粒中产生浓度梯度; 活性颗粒外部材料的膨胀受到内部材料的约束产生径向拉应力和切向压应力; 而内部未锂化区域未发生膨胀, 受到外部膨胀区域的拉伸产生径向拉应力和切向拉应力(图3(a))[12]。当锂离子离开活性颗粒时, 外部锂化区域的锂离子最先流失, 导致活性材料脱锂收缩; 活性颗粒外部材料的收缩受到内部材料的约束产生径向压应力和切向拉应力; 而内部未脱锂区域未发生收缩, 受到外部收缩区域的挤压产生径向压应力和切向压应力(图3(b))[12]。当扩散应力超过活性材料的强度极限时, 活性颗粒会产生开裂、破碎、粉化等多种形式的力学损伤[13]。由于常见活性材料的拉伸强度极限远小于压缩强度极限, 因此当扩散应力为拉应力时, 往往更容易造成颗粒的损伤。

活性颗粒尺度下与扩散应力有关的研究主要是通过建立活性颗粒的多物理场耦合模型, 获取活性颗粒内部的锂浓度分布和扩散应力分布, 以及活性颗粒的结构、材料参数及电化学性能与扩散应力之间的关系, 最终从力学的角度定性/定量地给出活性颗粒的设计和优化方法。还有一些学者研究了位错、预锂化、相分离、粘结剂、外部约束、表面包覆和充放电策略等因素对活性颗粒中扩散应力的影响。

2.1 单颗粒模型

在充放电过程中, 活性颗粒内部的扩散应力水平受到多种因素影响。如果能够改变这些因素, 就有可能降低扩散应力, 减少活性颗粒的力学损伤, 从而达到延长电池使用寿命的目的。

活性颗粒的尺寸和形状都会影响扩散应力。Liu等[14]通过透射电镜(TEM)实验观察了球形硅颗粒的锂化过程, 发现在2 V的充电电压下, 锂离子从外部电解质流入硅颗粒中, 形成锂化外层并导致颗粒发生膨胀(图4)。当颗粒直径小于150 nm时, 颗粒在锂化时表面不会发生开裂; 当颗粒直径大于150 nm时, 随着锂化外层的不断膨胀, 颗粒表面先发生开裂, 并最终发生破碎。Hu等[15]根据断裂力学推导了具有预裂纹的磷酸铁锂颗粒不发生裂纹扩展的临界尺寸critical:

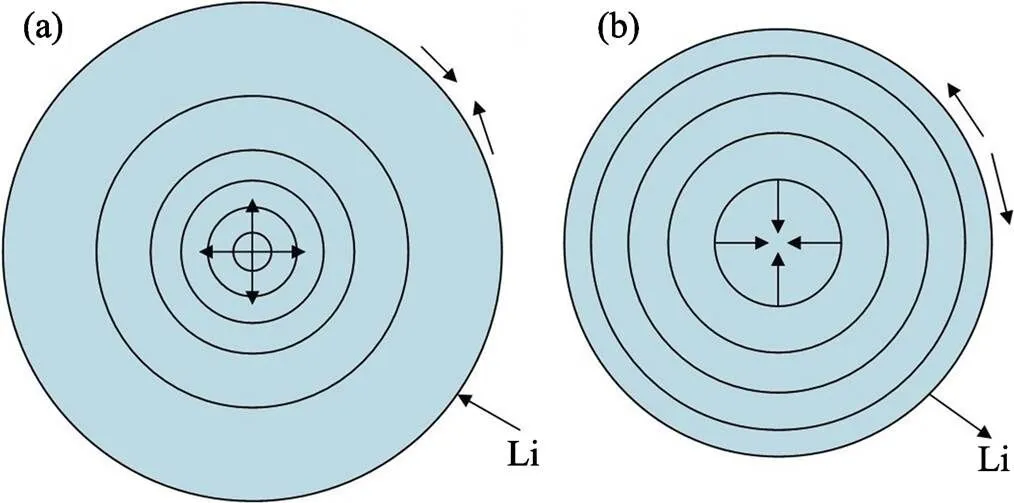
图3 活性颗粒中的径向应力和切向应力[12]

(a) Lithiation process; (b) Delithiation process

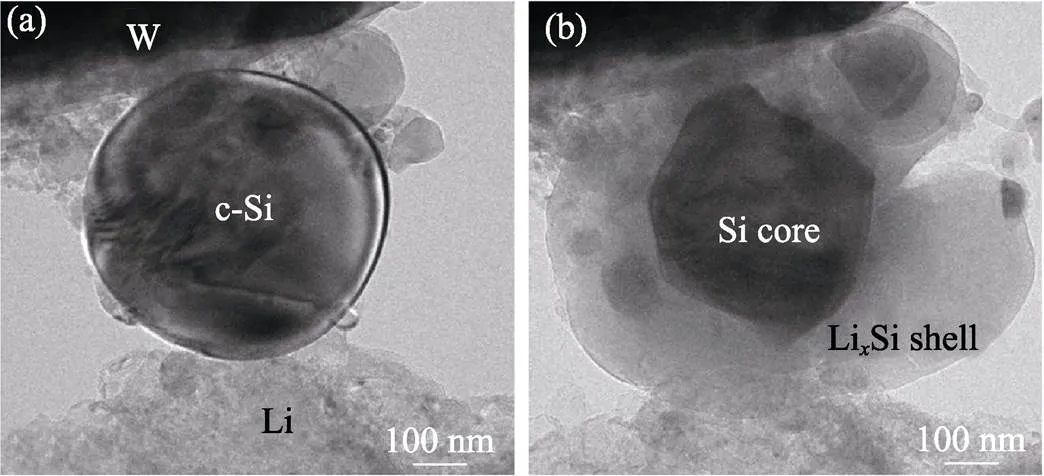
图4 球形硅颗粒的锂化过程[14]

(a) Initial state; (b) Outer layer expansion and surface cracking of the particle during lithiation

其中,为表面能,max为与边界有关的最大无量纲系数,为弹性模量,m为失配应变。当颗粒的特征尺寸低于临界尺寸critical时, 即使颗粒存在预裂纹也不会发生断裂。该结论适用于不同形状的颗粒。 Zhu等[16]分别建立了椭球形颗粒和球形颗粒的电化学–机械耦合模型, 研究了充放电时初始缺陷在两种颗粒中造成的裂纹扩展情况。对于球形颗粒, 电流密度越大, 颗粒直径越大, 最大主应力就越高, 颗粒初始缺陷造成的裂纹扩展就越严重; 对于椭球形颗粒, 当颗粒纵横比为1.5 : 1时最大主应力最高, 颗粒初始缺陷造成的裂纹扩展最严重。Purkayastha等[17]对比了立方形颗粒和球形颗粒在锂化和脱锂过程中的扩散应力分布, 发现在脱锂过程中, 立方形颗粒的最大主应力位于颗粒表面的棱边中点, 最大主应力的值高于球形颗粒表面的最大主应力; 而在锂化过程中, 立方形颗粒的最大主应力位于颗粒中心, 最大主应力的值与球形颗粒中心几乎相同。总体来看, 与椭球形和立方形的颗粒相比, 球形颗粒中的扩散应力水平较低, 更不容易在循环过程中产生裂纹。

空心颗粒结构的比表面积大、质量轻、单位体积负载量大, 物质传输路径短, 在锂离子电池领域具有良好的应用前景。Deluca等[18]分别建立了实心球形颗粒和空心球形颗粒的电化学–机械耦合模型, 发现在相同条件下的锂化过程中, 空心球形颗粒中的扩散应力水平远小于实心球形颗粒。陈等[19]研究了空心球形颗粒中的扩散应力分布, 计算结果表明锂化过程中颗粒内表面和外表面附近的切向应力较高, 而颗粒中间区域的径向应力较高。Li等[20]通过计算发现空心球形硅颗粒的内、外表面的锂浓度比越大, 颗粒内部的径向应力和切向应力就越大; 内、外表面的塑性变形可以有效降低不同锂化时刻下的径向应力和切向应力。

由于不同活性材料的锂化膨胀系数和材料力学参数不同, 因此活性颗粒的材料性质也对扩散应力具有重要影响。Zhang等[10]发现在恒定的外部锂浓度下, 球形颗粒径向和切向的锂化膨胀系数比越大, 颗粒内部的径向和切向应力越小。Zhao等[21]研究了活性材料的塑性变形对球形颗粒扩散应力的影响, 发现径向塑性变形大于切向塑性变形的活性材料更利于降低颗粒在锂化过程中的径向和切向应力。Li等[22]研究了应变率对球形硅颗粒中扩散应力的影响, 发现与未考虑应变率相比, 考虑应变率后切向应力和径向应力水平均降低了, 并且电流密度越大, 应变率对径向应力和切向应力的影响越大。

纳米线颗粒和纳米管颗粒是目前极具应用前景的一类活性颗粒类型。这类颗粒通常为直径较小的细长线状或管状结构, 很容易发生断裂。Ma等[23]通过电化学–机械耦合模型研究了纳米线颗粒中的扩散应力分布情况(图5(a))。在锂化过程中, 从颗粒中心到颗粒表面, 径向应力从最大值逐渐减小到0且始终为拉应力; 切向应力从最大拉应力逐渐减小到0, 然后转变为压应力且不断增大; 轴向应力始终为压应力且不断增大。Ryu等[24]研究了具有预裂纹的硅纳米线颗粒的裂纹扩展现象, 发现在锂化前期和脱锂后期颗粒的能量释放率最大, 可能造成严重的裂纹扩展而导致颗粒断裂; 减小颗粒的直径能够有效抑制裂纹扩展。Hardin等[25]建立了具有初始分层缺陷的硅纳米线颗粒的模型(图5(b)), 计算结果表明材料的屈服强度越小、颗粒的纵横比和半径越小, 锂化过程中的最大能量释放速率就越小, 可以减轻颗粒与集流体的分层现象。Lee等[26]通过扫描电镜(SEM)和仿真计算研究了受到机械夹持的硅纳米线颗粒的锂化过程(图5(c)), 发现机械夹持可以限制颗粒的锂化膨胀并在颗粒内部引起压应力; 该压应力降低了锂化过程中的最大拉应力, 从而增强了颗粒的抗断裂能力。Chen等[11]根据应变能理论推导了恒流充电条件下纳米线颗粒不发生断裂的临界半径:

图5 (a)纳米线颗粒及其锂化过程[23]; (b)具有初始分层缺陷的纳米线颗粒的初始状态和锂化膨胀状态[25]; (c)受到机械夹持的纳米线颗粒的初始状态和锂化膨胀状态[26]

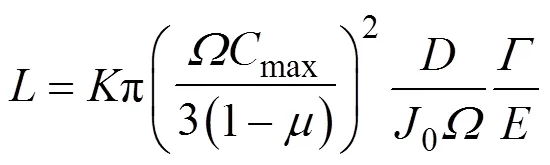
其中,max为颗粒中的最大锂浓度,为偏摩尔体积,为锂扩散系数,为弹性模量,为泊松比,0为充电倍率,为断裂能,为与裂纹长度和时间有关的无量纲系数。此外, 部分学者还研究了预锂化[27]、偏摩尔体积[28]、介质膨胀速率[29]、锂扩散系数的锂离子浓度依赖性[30]、弹性模量及其锂离子浓度依赖性[30]等参数对纳米线或纳米管颗粒中扩散应力的影响。

采用特定材料对活性颗粒进行包覆可以提高活性颗粒的导电性和稳定性等, 已经在锂离子电池领域得到了广泛应用。碳材料具有良好的导电性和力学性能, 成本较低, 是目前最常用的包覆材料之一。Hao等[31]建立了碳包覆的实心球颗粒的电化学–机械耦合模型(图6(a)), 发现碳包覆外壳可以有效降低活性颗粒内核的径向拉应力和切向拉应力。孙等[32]进一步对比了碳包覆的实心球颗粒和空心球颗粒, 发现在锂化和脱锂过程中, 碳包覆的空心球颗粒中的锂离子浓度分布比实心球颗粒更均匀, 因而扩散应力水平也更低(图6(b))。Hao等[33]研究了碳包覆外壳对纳米管颗粒中扩散应力的影响(图6(c)), 发现较薄的碳壳能够降低锂化和脱锂过程中颗粒内表面的切向拉应力, 但增大了脱锂过程中碳壳内的切向拉应力, 因此碳壳的厚度应当取适中的值。除此以外, Zhao等[34]研究了包覆硅纳米管颗粒的氧化铝外壳中的扩散应力, 发现外壳厚度越薄, 外壳与硅核发生界面脱离的概率越小, 但外壳发生断裂的概率越大。

根据活性材料在锂脱嵌过程中是否发生相分离, 活性颗粒的锂脱嵌可分为单相脱嵌机制和双相脱嵌机制。对于双相脱嵌机制材料(如磷酸铁锂等), 锂化相和未锂化相之间存在明显的相界面, 在相界面处锂浓度梯度急剧变化; 对于单相脱嵌机制材料(如石墨等), 从活性颗粒中心到表面的锂浓度是连续变化的。Deshpande等[35]研究了双相脱嵌机制的球形颗粒在脱锂过程中的扩散应力(图7(a)), 发现切向应力会在相界面处发生急剧变化; 锂化相和未锂化相的锂离子平衡浓度比和弹性模量比越大, 相界面处的切向应力变化越大, 颗粒越容易在相界面处发生分离。Drozdov等[36]研究了双相脱嵌机制的球形颗粒在锂化过程中的扩散应力, 结果表明颗粒表面的切向应力在锂化初始阶段先从0增加到最大压应力, 然后逐渐减小到0并转变为拉应力(图7(b)), 因而在锂化结束时更容易发生表面破裂。Huang等[37]通过计算发现在不完全放电后的短时间内再次充电后, 单相脱嵌机制的球形颗粒外层的切向应力仍然为压应力, 而双相脱嵌机制的球形颗粒外层出现较大的切向拉应力, 因而易于产生裂纹。总体来说, 双向脱嵌机制的活性颗粒中更容易存在拉应力或较高的应力梯度。

图6 (a)具有碳包覆外壳的实心球颗粒[31]; (b)碳包覆的实心球颗粒与空心球颗粒在锂化过程中的锂浓度分布[32]; (c)具有碳包覆外壳的的纳米管颗粒[33]

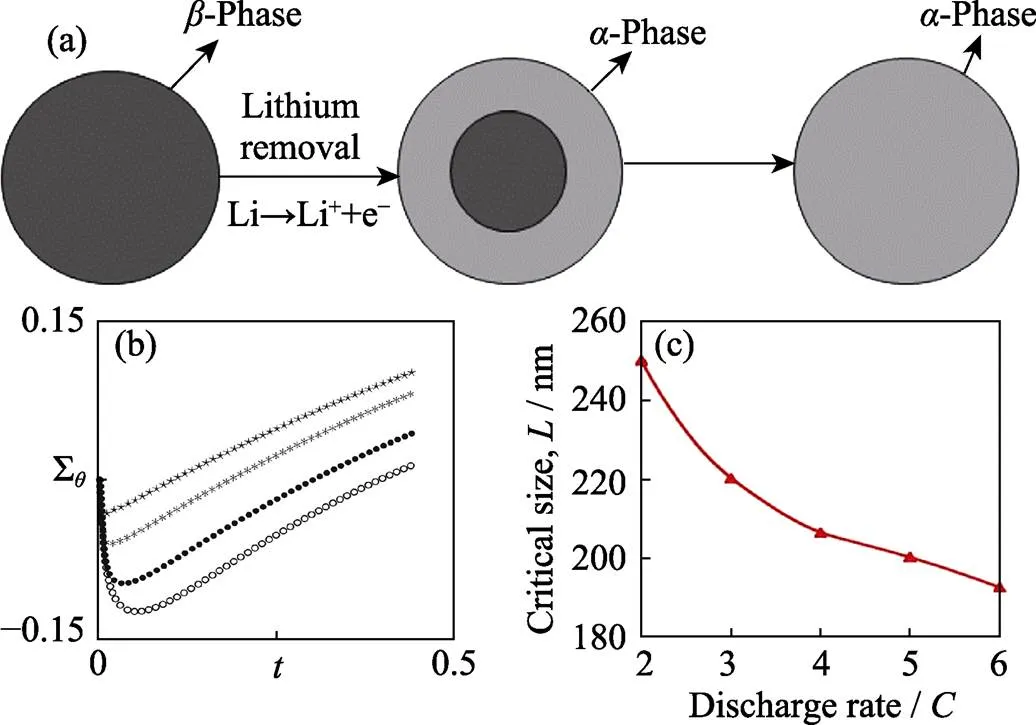
图7 (a)双相脱嵌机制的球形颗粒的脱锂过程[35]; (b)双相脱嵌机制的球形颗粒锂化过程中的表面切向应力[36], 其中空心圆, 实心圆, 星号和星形分别代表颗粒的初始无量纲尺 寸为0.01, 0.1, 1.0和10.0; (c)临界尺寸L与放电倍率的关 系[42]

位错是由原子的局部不规则排列造成的晶体材料内部的微观缺陷。在外力作用下, 位错会发生移动并导致宏观变形, 从而影响材料的力学性能。Liu等[38]通过实心球颗粒的电化学–机械耦合模型研究位错对充电过程中扩散应力的影响, 发现与没有考虑位错相比, 考虑了材料位错的活性颗粒内部的切向拉应力和径向拉应力都较小。魏等[39]也得到了类似的结论。Zhu等[40]和Li等[41]还分别研究了位错对空心球颗粒和纳米线颗粒中扩散应力的影响。总体来说, 由于位错产生的移动可以消耗一部分弹性应变能, 减小锂化引起的弹性膨胀, 因此有助于降低颗粒内部的扩散应力。

充放电的倍率和策略会影响活性颗粒中的锂浓度及分布, 从而影响扩散应力。Zhao等[42]研究了放电倍率对钴酸锂颗粒中扩散应力的影响, 发现放电倍率越高, 颗粒中的锂浓度分布越不均匀, 扩散应力也越大; 并通过仿真计算得到了放电倍率与颗粒不发生破裂的临界尺寸的关系(图7(c))。Lu等[43]计算了恒流–恒压(CC-CV)充电策略对扩散应力的影响, 发现充电电流越大, 恒流–恒压的切换时刻越早, 充电过程中的最大应力越高。而赵等[44]研究了CC-CV充电策略中恒流阶段和恒压阶段的充电中断对扩散应力的影响, 发现充电中断的持续时间越长, 充电中断引起的应力涨落越剧烈。Li等[4]结合恒流和恒压充放电的特点提出了恒流充电–恒压充电–恒流放电–恒压放电的四阶段充、放电策略, 可以有效降低整个充、放电过程中球形硅颗粒内部的平均扩散应力。

表1总结了单颗粒模型中影响扩散应力的因素。

2.2 多颗粒模型

在多孔复合电极中, 活性颗粒通常紧密地排列在一起, 粘结剂和导电剂分布在颗粒之间的间隙中。在充放电过程中, 锂离子扩散引起的浓度梯度导致活性颗粒内部产生扩散应力; 由于受到周围相邻颗粒、粘结剂、导电剂和集流体等材料的外部约束, 活性颗粒在锂化和脱锂过程中的体积膨胀和收缩也会导致内部产生扩散应力。通过多颗粒模型可以研究多孔电极内部扩散应力的分布和演变情况, 以及不同因素对扩散应力的影响规律。

Kim等[45]通过多颗粒电化学–机械耦合模型研究锂化过程中磷酸铁锂球形颗粒的扩散应力及其影响因素, 发现较小的颗粒直径和放电倍率有助于降低颗粒内部和表面的扩散应力。Ji等[46-47]进一步 考虑电极中活性颗粒的尺寸分散性; 发现充放电时在多颗粒结构的电极内部均存在不均匀分布的锂浓度(图8(a)), 进而导致不均匀分布的扩散应力场; 减小活性颗粒的直径和尺寸分散性可以降低颗粒内部的扩散应力, 并使多孔电极中扩散应力的分布更均匀。但是, 这类多颗粒模型的结构比较简单, 没有考虑粘结剂、导电剂和相邻颗粒等外部约束对扩散应力的影响。

表1 单颗粒模型中影响扩散应力的因素

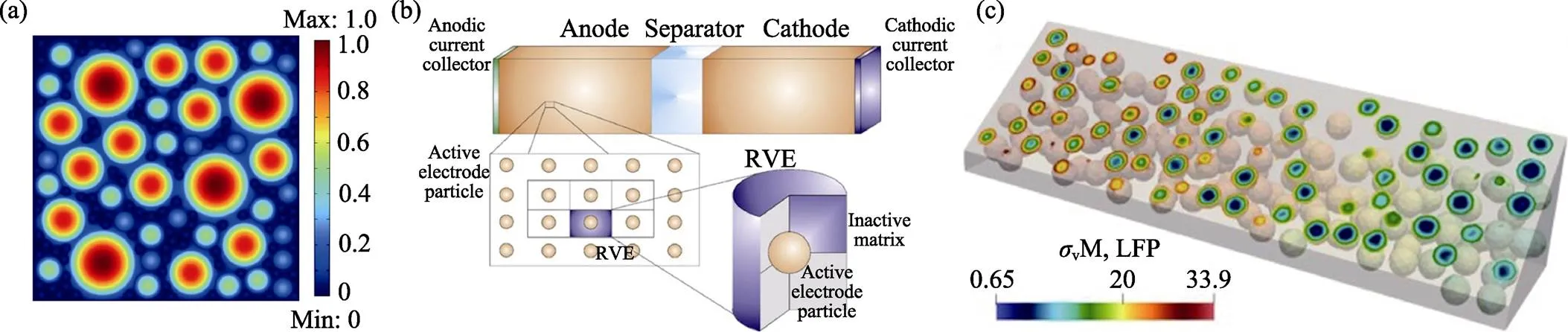
图8 (a)放电深度为60%时多颗粒模型中的锂浓度分布[46-47]; (b)考虑均匀基质的多颗粒模型及单颗粒–基质的代表性单元[48]; (c)考虑均匀基质的多颗粒–基质的电极结构及1C放电时活性颗粒的扩散应力分布[50]

部分学者将粘结剂和导电剂简化为包裹活性颗粒的均匀基质材料, 考虑了它们对多颗粒模型中扩散应力的影响。Dimitrijevic等[48]以单个球形颗粒与基质材料组成的代表性单元(RVE)为研究对象, 建立了考虑基质结构的硅锡复合材料多颗粒模型 (图8(b)); 发现活性颗粒的半径越大、活性颗粒之间的间距越小, 活性颗粒和基质界面上的拉应力就越大。Xu等[49]建立了由多个球形硅颗粒与基质材料组成的模型, 结果表明基质材料和颗粒材料的弹性模量比越大、颗粒之间的间距越小, 颗粒内的扩散应力水平就越高。Mai等[50]将研究对象进一步扩展为更多的颗粒和基质材料组成的结构, 建立了由磷酸铁锂球形颗粒和粘结剂基质组成的多颗粒模型(图8(c)); 发现颗粒和粘结剂中的最大Von Mises应力均随着锂化时间的延长和粘结剂弹性模量的增加而增大。

在有些多颗粒模型中, 粘结剂和导电剂与实际结构和形状更加接近。如Renganathan等[51]建立了具有球形和椭球形粘结剂和导电剂的石墨负极的多颗粒电化学–机械耦合模型, 发现放电倍率越大, 颗粒中的扩散应力越大; 负极的厚度和颗粒尺寸越小、孔隙率越大, 颗粒中的扩散应力就越小。Rahani等[52]研究了粘结剂对石墨负极扩散应力的影响, 计算结果表明粘结剂的屈服强度越小、含量越低, 各颗粒中的平均应力就越小; 采用壳状粘结剂的各颗粒中的平均应力小于采用桥状粘结剂的颗粒。总体来说, 较小的颗粒直径、较大的颗粒间距、较一致的颗粒尺寸、较小的基质弹性模量和较低的放电倍率都有助于降低颗粒中的扩散应力。

在上述模型中, 活性颗粒都是抽象得到的规则形状, 然而在实际情况中, 活性颗粒的形状通常并不规则。借助三维扫描技术可以获取电极的实际微观结构, 从而重建与实际情况更加吻合的多颗粒模型。Mendoza等[53]根据X射线断层扫描得到的钴酸锂正极的三维微结构, 建立了多颗粒电化学–机械耦合模型(图9(a)), 通过计算发现电极中的平均Von Mises应力随着充电时间的延长而线性增大; 颗粒表面的粘结剂能够显著降低颗粒内部的拉应力, 甚至将部分区域的拉应力转变为压应力, 使颗粒更不容易破裂。Wu等[54]采用同样的方法扫描得到了NMC111正极(NMC指三元复合正极材料LiNiMnCoO2, 其中++=1, 111指镍、锰、钴三种元素的配比, 即::=1 : 1 : 1)的模型, 并研究了电极内部的扩散应力分布情况(图9(b))。结果表明与导电网络分离的活性颗粒由于没有锂离子嵌入, 因此几乎没有扩散应力(Case A); 最大扩散应力出现在颗粒之间相互连接的狭小区域(Case B), 容易导致颗粒的断裂; 在颗粒之间没有相互连接的自由表面附近(Case C), 颗粒表面的扩散应力大于颗粒内部。

3 活性电极尺度下的扩散应力

锂离子电池的正/负极片通常由正/负极活性层和集流体构成。其中活性层是由活性材料、粘结剂和导电剂等成分组成, 为多孔颗粒复合材料, 集流体为金属薄片, 正极通常采用铝箔, 负极通常采用铜箔。正/负极片被多孔的隔膜分隔, 电解液填充在隔膜与活性层的微孔内, 为电化学反应输运锂离子, 而集流体的作用是输运电子。在充放电循环中, 锂离子在活性材料内的扩散会引起活性层的膨胀或收缩, 在集流体的约束作用下产生扩散应力; 同时, 锂离子的扩散过程也会引起不均匀的浓度分布, 进而导致不均匀的变形, 在活性材料内部也会产生扩散应力。因此, 锂离子在活性层中的扩散和集流体对活性层的约束是活性电极尺度下产生扩散应力的主要原因, 活性材料的性质、活性层的结构以及集流体的厚度、弹性模量、塑性变形和预应变等都会对扩散应力产生影响。

按照结构的不同, 在活性电极尺度下与扩散应力有关的模型主要有电极单元、薄膜电极、双层电极和对称电极等, 其中电极单元是从活性层中提取的代表性微元, 薄膜电极仅由活性层组成, 双层电极的集流体仅有一面涂抹活性层, 而对称电极的集流体两面都涂抹活性层。该尺度下与扩散应力有关的研究主要是通过将活性层简化为均质材料, 建立电极单元、薄膜电极、双层电极或对称电极的多物理场耦合模型, 研究活性层、集流体、活性层–集流体界面等不同方面的因素对电极力学和电化学性能的影响。

3.1 电极单元和薄膜电极模型

电极单元模型通常是从电极的活性层中提取某个代表性微元, 并假设锂离子在微元内部扩散而产生浓度梯度; 同时在微元外部施加约束条件, 以模拟周围活性材料或集流体的约束作用。而薄膜电极模型通常提取一部分具有完整厚度的活性层作为研究对象, 锂离子在活性层中扩散而产生浓度梯度, 活性层的底面施加约束条件以模拟集流体的约束作用。齐等[55]通过电化学–机械耦合模型研究了圆柱形和平板形磷酸铁锂电极单元在锂化过程中的扩散应力分布(图10(a)), 发现锂浓度均在锂离子的扩散方向上逐渐降低, 导致边界处的扩散应力最小而远离边界的扩散应力最大。Liu等[56]研究了硬币形硅薄膜电极中的扩散应力分布及其影响因素(图10(b)), 发现锂化过程中的最大主应力集中在侧面以及靠近侧面的顶面边缘, 使这些地方的电极材料更容易发生断裂。

活性材料的性质和局部缺陷都会影响电极中的扩散应力。Gao等[57]通过建立具有外部约束和预裂纹的电极单元模型, 发现活性材料的塑性变形可以有效降低电极内部的扩散应力水平, 从而提高电极的抗断裂能力。因此应当尽量采用塑性较强的活性材料。Chen等[58]建立了考虑位错的硅薄膜电极的电化学–机械耦合模型(图10(c)), 发现在恒压和恒流充电的任何时刻, 位错都降低了电极中的拉应力, 使电极更不易断裂。Wu等[59]建立了锰酸锂电极单元模型, 计算结果表明电极单元中存在的椭圆形的电化学惰性区(由局部缺陷形成的不参与任何电化学反应的区域)会造成不均匀的扩散应力分布, 这一方面可能导致活性颗粒的开裂, 另一方面还可能导致粘结剂的失效和活性颗粒之间的分离。因而在生产时应当尽量减少活性材料的内部缺陷。

3.2 双层电极和对称电极模型

将薄膜电极模型的约束条件替换为集流体, 可以得到双层电极模型。在集流体的另一侧表面上再增加一层活性层, 可以得到对称电极模型。在双层电极和对称电极中, 扩散应力诱导的主要失效形式是活性层与集流体的分层和活性层的断裂[60]。当活性层–集流体界面的应力差过大时, 活性层与集流体会发生界面滑动和分层等失效现象; 当活性层自由表面的扩散应力过大时, 会使活性层表面产生裂纹, 甚至造成活性层的断裂。

由于集流体对活性层的约束作用, 集流体的弹性模量、塑性变形、厚度和预应变等都会对电极中的扩散应力产生影响。Ji等[61]通过双层电极模型发现, 集流体和活性层的弹性模量比越小, 活性层–集流体界面上的应力差和活性层自由表面上的扩散应力就越小。宋等[62]和Song等[63]分别建立了石墨活性层–铜集流体的双层电极(图11(a))和对称电极(图11(b))的电化学–机械耦合模型, 发现在充、放电过程中, 集流体的塑性变形可以减弱其对活性层的约束, 从而降低集流体和活性层中的扩散应力。Liu等[64]发现集流体的弹性模量和屈服极限越小, 界面的分层程度就越小, 这与Ji等和宋等的结论是一致的。此外, Liu等[65]和Hao等[66]还分别研究了集流体的厚度和预应变对双层电极中扩散应力的影响。总体来说, 较柔软的、塑性较强的集流体更利于减小电极中的扩散应力, 降低电极的失效概率。

活性材料的性质、组分和活性层的结构也会影响电极中的扩散应力。Lu等[5]建立了锡双层电极的电化学–机械耦合模型, 计算表明活性层的蠕变可以降低恒流充电时集流体和活性层中的扩散应力水平。Song等[67]研究了考虑单相脱嵌机制和双相脱嵌机制的双层电极中的扩散应力; 在充电时单相电极沿活性层厚度方向上的锂浓度连续变化, 而双相电极中的锂浓度在相界面处急剧变化, 因而扩散应力更大, 也更容易断裂。Li等[68]考虑了活性材料的应变率, 发现硅双层电极中的最大扩散应力始终发生在活性层和基底界面附近, 容易造成活性层和集流体的分层。He等[69]比较了石墨/硅活性层–铜集流体对称电极中活性层弹性模量的锂浓度依赖性(图11(c))对扩散应力的影响。对于石墨活性层来说, 由于石墨材料的弹性模量随锂离子浓度的增大而增大, 活性层和集流体内扩散应力的水平都更高; 对于硅活性层来说, 由于硅材料的弹性模量随锂离子浓度的增大而减小, 活性层和集流体内的扩散应力的水平都更低。Liu等[70]发现在锡双层电极的活性层中添加石墨烯不仅可以降低活性层自由表面的最大扩散应力, 还可以降低活性层–集流体界面上的应力差。Zhang等[71]发现负指数梯度的活性层(活性材料的弹性模量在厚度方向呈负指数变化)对锰酸锂对称电极有三个作用, 首先可以降低活性层–集流体界面的应力差, 减少活性层与集流体的分层和滑移; 其次可以降低活性层自由表面的最大压应力, 从而减少活性层自由表面的失效; 最后可以降低充电过程中的能量释放速率, 减小电极发生断裂的可能性。Lu等[72]研究了硬币形双层电极模型的界面分层现象, 结果表明较小的活性层直径有助于降低充电末期的界面分层程度。

图10 模型示意图

(a) Cylindrical and plate electrode units[55]; (b) coin-shaped thin film silicon electrode[56]; (c) thin film silicon electrode considering dislocations[58]

图11 (a)考虑集流体塑性变形的双层电极的初始状态和锂化变形[62]; (b)石墨活性层和铜集流体组成的对称电极模型[63]; (c)石墨和硅的弹性模量随SOC的变化[69]

硅双层电极在第一次电化学循环后可能发生开裂而形成一系列硅岛, 这些硅岛起初与集流体保持连接, 在多个循环后可能与集流体部分或完全分层, 进而导致电池容量急剧下降。硅岛与集流体的分层通常需要经历裂纹成核、裂纹扩展和完全分层3个步骤。Pal等[73]建立了受到集流体约束的非晶硅岛的电化学–机械耦合模型(图12(a)), 发现硅岛与集流体界面的分层首先发生在硅岛的角部区域, 并随着电化学循环的进行逐渐向硅岛的中心区域传播。Haftbaradaran等[74]研究了预裂纹对受到基底约束的方形硅岛的影响。发现当中心位置没有预裂纹时, 方形硅岛不可能在中心位置产生裂纹成核和裂纹扩展现象; 但即使边缘位置没有预裂纹, 方形硅岛也能在边缘位置产生裂纹成核和裂纹扩展现象。Yang等[75]通过原位扫描电镜和仿真计算研究了具有不同初始缺陷的硅岛双层电极的断裂过程, 发现硅岛会在椭圆形初始缺陷的长轴尖端附近发生断裂, 这是由于此处的扩散应力最大; 椭圆形初始缺陷的长、短轴的长度比越大, 最大扩散应力越大, 硅岛发生断裂的时刻也越早(图12(b))。总体来说, 为了减少硅岛的裂纹扩展, 需要预防初始缺陷, 尤其是硅岛中心位置的缺陷以及线条形的缺陷。

图12 (a)硅双层电极发生开裂形成硅岛(上), 以及受到集流体约束的硅岛双层电极模型(下)[73]; (b)具有初始缺陷的硅岛双层电极在锂化后的扩散应力分布, 初始缺陷的长、短轴的长度比分别为0.2, 0.4, 0.6, 0.8和1[75]

4 半电池、电池单元和电池单体尺度下的扩散应力

4.1 半电池

在活性颗粒和活性电极等微观和介观尺度下, 目前常用的研究手段仍然以仿真计算为主。将电极与其他电池组分组装为半电池后, 可以通过实验测试手段观察电极的失效过程或获取电极内的扩散应力水平。半电池尺度下与扩散应力有关的实验研究通常是先在基底上制备工作电极, 再将工作电极、集流体、纯锂对电极、隔膜和电解液组装为半电池, 然后对半电池进行电化学循环, 同时采用显微可视化技术或者光学测量方法, 分析工作电极的力学和电化学性能。

通过对工作电极内部的微观结构进行可视化观察, 可以揭示电极失效的微观机理。Chen等[76]制备了铝掺杂锰酸锂电极/纯锂半电池并进行恒流电化学循环, 通过扫描电镜观察电极中活性颗粒的失效现象。发现在第一次充电过程中较大的颗粒更容易产生裂纹, 并在放电过程中裂纹扩展; 经过多次充放电循环后, 最终颗粒完全断裂。由此认为活性颗粒的断裂模式分为单次循环过程中拉应力过大导致的脆性断裂和多次循环过程中裂纹扩展导致的疲劳断裂。Xu等[77]制备了NMC311正极/纯锂半电池并进行5充放电循环, 通过X射线成像技术研究三元正极的失效现象。结果表明活性颗粒的断裂以及活性颗粒与粘结剂的分离是电极材料破坏的主要形式, 并且越靠近隔膜, 电极材料的破坏越严重(图13)。Yim等[78]发现在集流体的约束作用下, 硅碳复合负极体积膨胀引起的扩散应力会导致活性层与集流体的分层、活性颗粒的断裂以及活性颗粒与粘结剂的分离(图14)。Li等[79]制备了网状碳薄膜电极/纯锂半电池并进行充放电循环, 通过扫描电镜观察碳电极的形貌演化情况。结果表明网状碳薄膜电极在嵌锂后不易出现扭曲和断裂等形式的结构破坏, 具有良好的力学稳定性。

部分学者还研究了电极的结构或材料对其电化学和力学性能的影响。如Li等[80]通过扫描电镜观测了非晶硅电极/纯锂半电池中硅电极的裂纹扩展现象, 发现硅电极的厚度越小, 裂纹密度就越大, 开裂形成的硅岛的尺寸就越小(图15)。通过理论推导得到了硅电极不产生裂纹的临界厚度c:

图13 NMC311正极中颗粒的失效情况[77]

(a) Three-dimensional view of the electrode; (b) Views of the location near the separator and the current collector

图14 (a)循环前、(b)后硅碳复合负极的扫描电镜照片[78]

其中,c为与断裂韧性有关的抗断裂强度,为弹性模量,为泊松比,为电极的应力。Zhang等[81]通过多光束光学传感器和扫描电镜研究了半电池中氧化硅电极的扩散应力, 发现在第一次循环过程中, 初始电极内的孔隙不仅能够容纳颗粒的体积膨胀, 减缓压应力的上升, 而且能够促进颗粒的重新排列, 改善电极内部的导电网络; 因此建议应在保证能量密度的前提下, 尽可能提高氧化硅电极的孔隙率。Qu等[82-83]制备了具有不同纳米结构的铝掺杂硅薄膜电极, 并通过扫描电镜研究了硅电极/纯锂半电池中铝掺杂硅薄膜电极在充放电循环时的表面形态和微观结构。结果表明硅电极的纳米孔结构能有效促进电解质的渗透并容纳活性材料的体积变化, 从而降低电极中的扩散应力。Zhang等[84]通过集流体剥离实验和扫描电镜研究了粘结剂/溶剂体系对锰酸锂电极性能的影响。在所考虑的4种粘结剂/溶剂体系中, 聚丙烯酸(Poly-Acrylic Acid, PAA)粘结剂/N-甲基吡咯烷酮(-Methyl Pyrrolidone, NMP)溶剂体系的锰酸锂电极在多次电化学循环后的容量衰减最小, 这是由于采用该粘结剂/溶剂体系后, 一方面活性层与集流体的粘结强度最高, 活性层与集流体不易发生分层破坏; 另一方面电极中二次颗粒的尺寸和尺寸分散性都最小, 有助于降低颗粒中的扩散应力, 并使不同颗粒间的扩散应力分布更均匀。

除了上述内容以外, 有些研究还通过光学方法测量得到基底的应变, 再由此计算出工作电极中的扩散应力水平。如Sethuraman等[85]制备了石墨电极/纯锂半电池, 利用多光束光学传感器和晶圆曲率法测试得到了石墨电极中的扩散应力, 发现在第一次锂化过程中, 扩散应力始终保持压应力, 并且在锂化结束时达到峰值; 在第一次脱锂过程中, 电极内的压应力先迅速降低到0, 然后转变为拉应力并增大到峰值(图16(a))。Pharr等[86]制备了非晶锗电极/纯锂半电池并进行恒流电化学循环, 结果表明在锂化过程中, 锗电极中的压应力先迅速增大, 然后逐渐减小; 在脱锂过程中, 锗电极中的压应力先迅速减小到0, 然后转变为拉应力(图16(b))。

图15 硅电极的裂纹扩展现象[80]

(a) Fresh electrode; (b) Electrode of 1000 nm thickness after 5 cycles; (c) Electrode of 500 nm thickness after 5 cycles; (d) Electrode of 200 nm thickness after 10 cycles

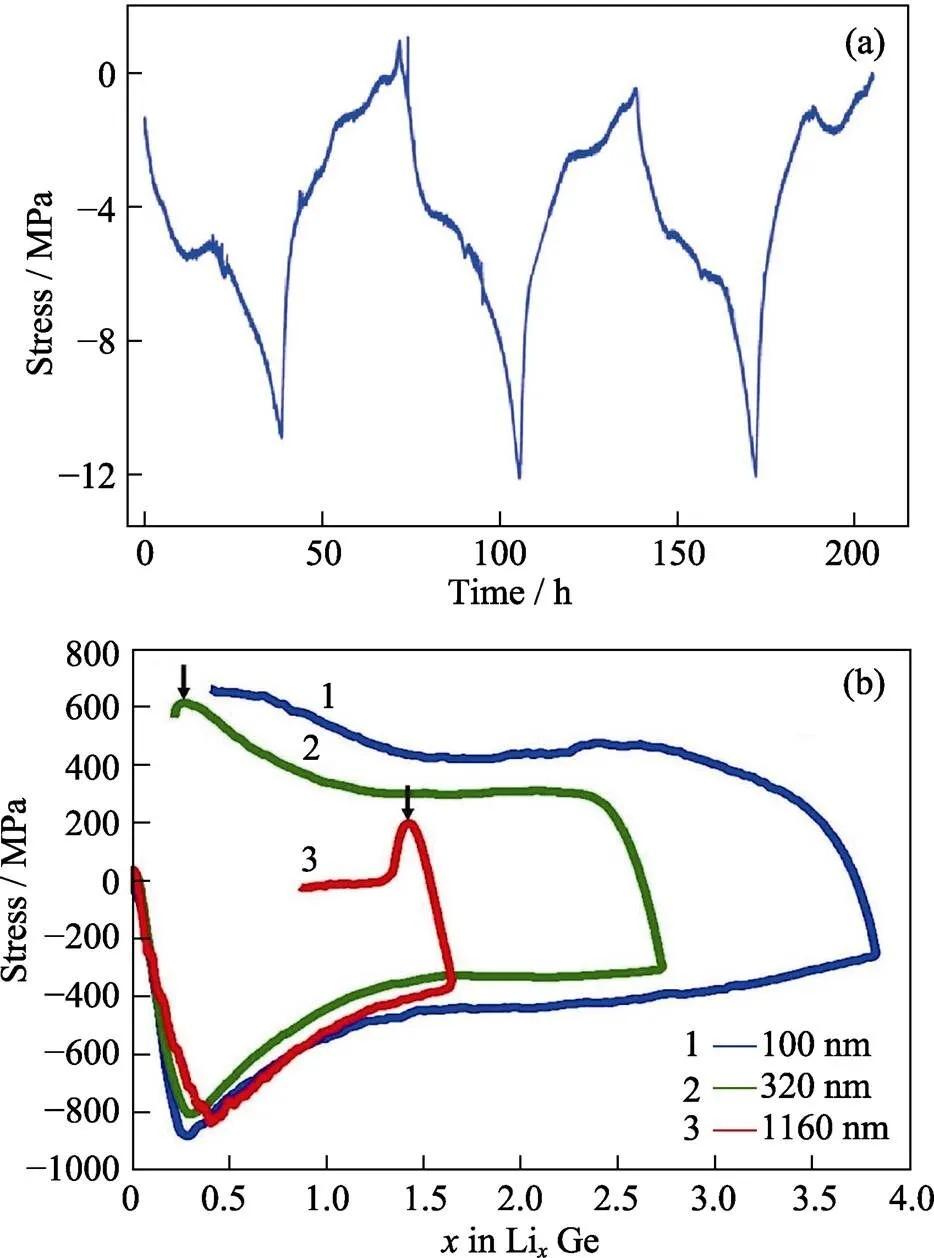
图16 (a)前三个循环期间石墨负极中的扩散应力[85]; (b)锂化和脱锂期间锗电极中扩散应力的演变, 其中箭头代表电极发生断裂的时刻[86]

4.2 电池单元

电池单元由正极片、负极片、隔膜和电解液组成。电池单元尺度下扩散应力的研究可以通过实验或仿真手段进行。数值仿真研究通常是建立包含一组正极片–隔膜–负极片的电池单元的多物理场耦合模型, 极片中的活性层采用多孔颗粒结构或均质材料结构。通过仿真计算得出电化学循环过程中电极内的扩散应力, 并进一步研究扩散应力的影响因素或扩散应力对电池性能的影响规律。

通过仿真计算可以得到电化学循环过程中电池单元内扩散应力的分布情况。Suthar等[87]建立了钴酸锂/石墨电池单元的电化学–机械耦合模型, 发现在整个充电过程中石墨负极的最大径向应力和最大切向应力都出现在靠近隔膜的活性颗粒中。Yang等[88]通过计算发现, 在放电初期, 磷酸铁锂/石墨电池单元中隔膜附近的负极颗粒表面的切向应力最大。Wu等[89]建立了锰酸锂/石墨电池单元模型, 发现在循环过程中负极的最大第一主应力出现在放电结束时活性颗粒的表面, 而正极的最大第一主应力出现在放电和充电结束时活性颗粒的中心。总体来说, 充放电过程中靠近隔膜的负极颗粒容易产生较高的扩散应力。

通过电池单元模型也可以研究不同设计变量对扩散应力的影响。Fu等[8]研究了充放电循环中锰酸锂/石墨电池单元中的扩散应力。计算结果表明倍率越大, 正极和负极中的扩散应力也越大; 静置过程中锂离子浓度梯度逐渐减小到0, 扩散应力也逐渐降低到0。Dai等[7]通过计算发现在锰酸锂电极中添加镍钴铝成分(NCA)会增大放电早期颗粒中的最大径向应力, 但会显著降低放电末期的最大径向应力, 因此应当折中考虑选择适当的NCA比例。Rieger等[90]研究了放电过程中正、负极耳的布置形式对钴酸锂/石墨电池单元中扩散应力的影响(图17), 发现对于极耳平行布置的电池单元, 放电初期极耳附近的扩散应力最大, 放电中期电池单元中部的扩散应力最大, 而放电末期远离极耳处的扩散应力最大; 对于极耳对称布置的电池单元, 放电初期极耳附近的扩散应力最大, 放电后期电池单元中部的扩散应力最大; 但整体来说极耳平行布置的电池单元中正、负极的最大扩散应力大于极耳对称布置的电池单元。

4.3 电池单体

在电池单体尺度下, 扩散应力一部分来源于上述活性电极尺度下产生的扩散应力, 另一部分则是外部约束造成的。在电池单体的充电过程中, 负极活性层处于富锂状态, 发生膨胀变形, 而正极活性层处于贫锂状态, 发生收缩变形; 放电过程则刚好相反; 电池单体的整体变形为正、负极活性层共同作用的结果。当电池单体受到外壳(如圆柱电池和方形电池)或装配(如软包电池)约束时, 就在电池单体尺度下产生扩散应力。循环变化的高水平扩散应力会造成电池中各组分的变形甚至损伤, 最终导致容量衰减、阻抗上升和寿命缩短等失效现象。

图17 放电期间电池单元中的扩散应力分布, 放电深度分别为(a) 8%, (b) 54%, (c) 67%和(d) 100% [90]

由于电化学–机械耦合模型的计算量普遍较大, 对于动辄具有几十甚至上百个电池单元的电池单体来说目前还难以直接采用, 因此该尺度下与扩散应力有关的研究通常以实验手段为主。一般采用外部夹具或约束装置对电池单体施加外部压力或约束, 同时进行电化学循环, 研究外部压力或约束对电池单体电化学性能和力学性能的影响。

在常用的锂离子电池中, 负极材料的锂化膨胀系数通常比正极材料大, 因而会导致充电过程中电池的厚度增加, 而放电过程中电池的厚度减小。Rieger等[91]通过激光扫描技术研究了钴酸锂/石墨软包电池在充电过程中不同位置的厚度变化情况, 发现电池的整体厚度随着SOC的增加而增大。充电前期不同位置的厚度变化几乎是均匀的, 而充电后期极耳附近的厚度变化远高于其他位置。张等[92]研究了磷酸铁锂/石墨软包电池在充放电循环过程中的变形情况。在高倍率充电时, 电池持续膨胀; 在低倍率充电时, 电池在充电初期和后期膨胀, 在充电中期收缩。在高倍率放电时, 电池在放电初期和中期收缩, 在放电后期膨胀; 在低倍率放电时, 电池在放电初期和后期收缩, 在放电中期膨胀。于等[93]对锰锂氧化物/石墨方形电池施加了外部固定约束, 采用应变式测力传感器测量2充放电过程中电池表面的压力变化情况(图18)。结果表明无论是充电还是放电过程, 电池表面的压力与SOC的关系总是分为3个阶段: 充电过程中先迅速增长, 达到大约50% SOC时基本保持不变, 达到80%SOC后又迅速增长; 而放电过程与此相反。

图18 方形电池在充放电过程中的表面压力的(a)实验原理图和(b)随SOC的变化曲线[93]

(a) Experimental schematic diagram; (b) Change of surface pressure with SOC

外部约束或压力也会对电池的电化学性能产生影响。Sauerteig等[94]通过电化学阻抗谱(EIS)研究了外部压力对电极和隔膜的离子输运性能的影响 (图19(a)), 发现随着外部压力的增大, 正极、负极和隔膜的离子输运阻抗也不断增大, 这可能是由于正极、负极和隔膜的多孔结构不断压缩, 导致其孔隙率减小, 迂曲度增大造成的。Barai等[95]采用外部约束夹具对NMC111/石墨软包电池施加不同的外部压力并进行充放电循环, 发现在0、0.03和0.1 MPa的外部压力下, 电池在1200次循环后的阻抗上升分别为7.5%、39%和18%(图19(b))。这可能是由于当外部压力较小时, 压力使隔膜产生蠕变, 隔膜的孔隙率降低, 离子传输阻抗上升; 而当外部压力较大时, 压力使活性颗粒与电解液接触更充分, 导致活性颗粒与电解液之间的离子传输阻抗降低。总体来看, 电池的阻抗随外部压力的增加而增大; 但是当外部压力达到一定程度后, 阻抗又会减小。

外部约束或压力也与电池的循环寿命有关。Cannarella等[96]通过压缩试验机和约束夹具对锂钴氧化物/石墨软包电池施加外部压力并进行充放电循环, 发现与无约束、0.5和5 MPa外部压力相比, 在0.05 MPa外部压力下电池的容量衰减最小 (图19(c))。Wünsch等[97]采用约束夹具对NMC622/石墨软包电池施加了不同类型的外部约束, 同时进行了循环老化实验和峰值功率实验。结果表明在无外部约束、恒定厚度约束、弹性元件约束和恒力弹簧约束4种条件下, 采用恒力弹簧约束的电池循环寿命最长, 在无外部约束时循环寿命最短(图19(d))。Li等[98]通过激光扫描装置测量了无约束的NMC111/石墨软包电池在循环过程中的体积变化情况, 发现在寿命末期电池会产生较大的不可逆形变; 如果电池模组采用刚性约束, 可能造成电池内部的压力升高; 因此在设计电池组结构时, 应当设置缓冲层以提供合适的外部约束。

但是, 上述研究没有详细说明为什么不同的外部压力水平会影响电池的循环寿命。Mussa等[99]采用高精度弹簧夹具对NMC111/石墨软包电池施加不同水平的外部压力并进行充放电循环, 发现与0.66、0.99和1.98 MPa外部压力相比, 1.32 MPa时电池的容量衰减最慢。这可能是由于外部压力可以抑制活性颗粒表面的SEI膜的破裂和屈曲, 减少活性颗粒与电解质的副反应, 从而抑制SEI膜的再生, 降低可循环锂的不可逆损失。张军等[100]采用外部加压装置对卷绕工艺的软包电池施加不同的外部压力并进行充放电循环, 发现当施加1 kN外部压力时, 电池的容量衰减最小; 而当外部压力超过2 kN时, 电池负极片会发生断裂; 当不施加外部压力时, 负极片与隔膜之间容易发生析锂; 两者都会导致电池产生严重的容量衰减。总体来说, 为了尽可能延长电池的使用寿命, 外部压力应当在一定范围内取适中值。

图19 (a)外部约束和EIS测试的实验原理[94]; (b)不同外部压力下阻抗随循环次数的变化[95]; (c)外部约束对电池循环寿命的影响, 蓝色、绿色、黄色和红色线条分别代表0, 0.05, 0.5和5 MPa的外部约束[96]; (d)健康状态(State of Health, SOH)随循环次数的变化, 蓝色、红色、黄色和紫色线条分别代表无外部约束, 恒定厚度约束, 弹性元件约束和恒力弹簧约束[97]

除了上述针对软包电池或方形电池进行的研究以外, 也有部分研究关注圆柱电池中的扩散应力。Pfrang等[101]通过X射线扫描和激光显微镜研究存在中心针的18650圆柱电池的卷芯变形情况, 发现在长期充放电循环后卷芯会发生显著的变形, 并且中心针附近的卷芯变形最严重(图20)。卷芯的变形会引起正、负极和集流体的分层, 从而导致电池的容量衰减, 阻抗上升。因此可以通过提高活性层与集流体的粘结强度来改善圆柱电池的循环性能。Schuster等[102]通过实验发现NMC/石墨圆柱电池在循环初期容量衰减速率比较慢, 而从大约80%的残余容量开始, 容量衰减的速率突然迅速增加, 最终导致电池失效。Bach等[103]利用计算机断层扫描、拆解检查和电化学分析等辅助方法进一步研究上述容量跳水现象的原因, 发现电芯内部压力的不均匀分布会引起负极上的局部快速析锂, 从而导致锂的不可逆损失, 进而造成电池容量的急剧衰减。因而在设计电池外包装或模组结构时应尽量保证电池表面压力的均匀分布。

表2对以上与扩散应力有关的电池单体的失效现象及机理进行了总结。

图20 充放电循环后卷芯的变形情况(a)X射线扫描结果和(b)激光显微镜结果[101]

表2 与扩散应力有关的电池单体的失效现象及机理

5 总结与展望

扩散应力是锂离子电池力学研究领域的核心问题之一, 锂离子电池的多种失效现象均与扩散应力密切相关。与扩散应力有关的研究不仅关系到电池的安全性、可靠性和耐久性, 而且对高比能、大容量和长寿命的新型电池的研发至关重要。从上述国内外研究进展可以看出, 目前在活性颗粒、活性电极、半电池、电池单元和电池单体尺度下已经涌现了大量关于扩散应力诱导的锂离子电池失效机理的研究, 研究方法和技术手段都较为丰富和成熟。但是仍有一些关键问题需要进一步研究和解决:

(1)在活性颗粒和活性电极尺度下, 与扩散应力有关的建模通常需要对实际结构进行大量的简化和假设, 难以精确地反映电化学过程中电池的各项参数对扩散应力和电化学性能的实际影响; 需要进一步建立与实际情况更吻合的理论模型或有限元模型;

(2)由于电化学–机械耦合有限元模型的计算量较大, 目前电池单体尺度下与扩散应力有关的研究通常以实验为主; 随着计算机性能的不断发展与提高, 需要探索充放电过程中多层电池单体内部扩散应力的计算方法和分析手段;

(3)外部压力水平或约束形式会显著影响电池单体的循环寿命, 然而目前外部压力水平和分布与电池循环寿命及失效形式之间的关系尚未完全摸清, 与扩散应力有关的电池单体的失效机理仍不十分明确, 有必要进一步研究并明确上述关系, 为电池单体的压力设计和电池模组的约束设计提供参考依据;

(4)固态电池技术目前正处在快速发展过程中, 而当前与固态电池扩散应力有关的研究较少, 需要加强对固态电池中扩散应力的研究。

[1] WANG Q Y, WANG S, ZHANG J N,. Overview of the failure analysis of lithium ion batteries., 2017, 6(5): 1008.

[2] BELOVA I V, MURCH G E. Thermal and diffusion-induced stresses in crystalline solids., 1995, 77(1): 127–134.

[3] ZHAO Y, STEIN P, BAI Y,. A review on modeling of electro- chemo-mechanics in lithium-ion batteries., 2019, 413: 259–283.

[4] LI H L, SONG Y C, LU B,. Effects of stress dependent electrochemical reaction on voltage hysteresis of lithium ion batteries., 2018, 39(10): 1453–1464.

[5] LU Y J, CHE Q, SONG X,. Stress self-relaxation arising from diffusion-induced creep in bilayer lithium-ion battery electrode., 2018, 150: 164–167.

[6] CHOI Z S, KRAMER D, MÖNIG R,. Correlation of stress and structural evolution in Li4Ti5O12-based electrodes for lithium ion batteries., 2013, 240: 245–251.

[7] DAI Y L, CAI L, WHITE R E. Simulation and analysis of stress in a Li-ion battery with a blended LiMn2O4and LiNi0.8Co0.15Al0.05O2cathode., 2014, 247: 365–376.

[8] FU R J, XIAO M, CHOE S Y. Modeling, validation and analysis of mechanical stress generation and dimension changes of a pouch type high power Li-ion battery., 2013, 224: 211–224.

[9] MEI W X, DUAN Q L, QIN P,. A three-dimensional electrochemical-mechanical model at the particle level for lithium-ion battery., 2019, 166(14): A3319–A3331.

[10] ZHANG X Y, CHEN H S, FANG D N. Diffusion-induced stress of electrode particles with spherically isotropic elastic properties in lithium-ion batteries., 2016, 20(10): 2835–2845.

[11] CHEN B B, ZHOU J Q, PANG X M,. Fracture damage of nanowire lithium-ion battery electrode affected by diffusion- induced stress and bending during lithiation., 2014, 4(40): 21072–21078.

[12] CHRISTENSEN J, NEWMAN J. Stress generation and fracture in lithium insertion materials., 2006, 10(5): 293–319.

[13] SUN H H, MANTHIRAM A. Impact of microcrack generation and surface degradation on a nickel-rich layered Li[Ni0.9Co0.05Mn0.05]O2cathode for lithium-ion batteries., 2017, 29(19): 8486–8493.

[14] LIU X H, ZHONG L, HUANG S,. Size-dependent fracture of silicon nanoparticles during lithiation., 2012, 6(2): 1522–1531.

[15] HU Y H, ZHAO X H, SUO Z G. Averting cracks caused by insertion reaction in lithium–ion batteries., 2011, 25(6): 1007–1010.

[16] ZHU M, PARK J, SASTRY A M. Fracture analysis of the cathode in Li-ion batteries: a simulation study., 2012, 159(4): A492–A498.

[17] PURKAYASTHA R, MCMEEKING R. Stress due to the intercalation of lithium in cubic-shaped particles: a parameter study., 2016, 51(12): 3081–3096.

[18] DELUCA C M, MAUTE K, DUNN M L. Effects of electrode particle morphology on stress generation in silicon during lithium insertion., 2011, 196(22): 9672–9681.

[19] CHEN B B, ZHOU J Q, LIU Z. Effects of thermal diffusion in hollow lithium ion battery with spherical particle electrode., 2016, 38(3): 1–7.

[20] LI J, FANG Q H, WU H,. Investigation into diffusion induced plastic deformation behavior in hollow lithium ion battery electrode revealed by analytical model and atomistic simulation., 2015, 178: 597–607.

[21] ZHAO K J, PHARR M, CAI S Q,. Large plastic deformation in high-capacity lithium-ion batteries caused by charge and discharge., 2011, 94: s226–s235.

[22] LI Y, ZHANG K, ZHENG B,. Effect of local velocity on diffusion-induced stress in large-deformation electrodes of lithium-ion batteries., 2016, 319: 168–177.

[23] MA Z S, GAO X, WANG Y,. Effects of size and concentration on diffusion-induced stress in lithium-ion batteries., 2016, 120(2): 025302.

[24] RYU I, CHOI J W, CUI Y,. Size-dependent fracture of Si nanowire battery anodes., 2011, 59(9): 1717–1730.

[25] HARDIN G R, ZHANG Y, FINCHER C D,. Interfacial fracture of nanowire electrodes of lithium-ion batteries., 2017, 69(9): 1–5.

[26] LEE S W, LEE H W, RYU I,. Kinetics and fracture resistance of lithiated silicon nanostructure pairs controlled by their mechanical interaction., 2015, 6: 7533.

[27] CHANG S, MOON J, CHO K,. Multiscale analysis of prelithiated silicon nanowire for Li-ion battery., 2015, 98: 99–104.

[28] PENG Y Z, ZHANG K, ZHENG B L. Stress analysis of a cylindrical composition-gradient electrode of lithium-ion battery in generalized plane strain condition., 2016, 65(10): 1–8.

[29] PENG Y Z, LI Y, ZHENG B L,. Influence of local velocity on diffusion-induced stress and axial reaction force in a hollow cylindrical electrode of lithium-ion batteries with considering expasion rate of medium..,2018, 67(7): 27–35.

[30] DESHPANDE R, QI Y, CHENG Y T,. Effects of concentration-dependent elastic modulus on diffusion-induced stresses for battery applications., 2010, 157(8): A967–A971.

[31] HAO F, FANG D. Diffusion-induced stresses of spherical core- shell electrodes in lithium-ion batteries: the effects of the shell and surface/interface stress., 2013, 160(4): A595–A600.

[32] SUN F N, FENG L, BU J H,. Effect of stress on electrochemical performance of hollow carbon-coated silicon snode in lithium ion batteries., 2019, 68(12): 42–51.

[33] HAO F, FANG D. Tailoring diffusion-induced stresses of core-shell nanotube electrodes in lithium-ion batteries., 2013, 113(1): 013507.

[34] ZHAO K J, PHARR M, HARTLE L,. Fracture and debonding in lithium-ion batteries with electrodes of hollow core-shell nanostructures., 2012, 218: 6–14.

[35] DESHPANDE R, CHENG Y T, VERBRUGGE M W,. Diffusion induced stresses and strain energy in a phase-transforming spherical electrode particle., 2011, 158(6): A718–A724.

[36] DROZDOV A D. A model for the mechanical response of electrode particles induced by lithium diffusion in Li-ion batteries., 2014, 225(11): 2987–3005.

[37] HUANG S, FAN F, LI J,. Stress generation during lithiation of high-capacity electrode particles in lithium ion batteries., 2013, 61(12): 4354–4364.

[38] LIU Z J, ZHOU J Q, CHEN B B,. Interaction between dislocation mechanics on diffusion induced stress and electrochemical reaction in a spherical lithium ion battery electrode., 2015, 5(91): 74835–74843.

[39] WEI P F, ZHOU J Q, DENG K J,. Effect of dislocation on spherical particle electrode for lithium ion battery., 2015, (4): 719–722.

[40] ZHU J W, ZHOU J Q, CHEN B B,. Dislocation effect on diffusion-induced stress for lithiation in hollow spherical electrode., 2015, 20(1): 37–46.

[41] LI J, FANG Q H, LIU F,.Analytical modeling of dislocation effect on diffusion induced stress in a cylindrical lithium ion battery electrode., 2014, 272: 121–127.

[42] ZHAO K J, PHARR M, VLASSAK J J,. Fracture of electrodes in lithium-ion batteries caused by fast charging., 2010, 108(7): 073517.

[43] LU B, SONG Y C, ZHANG J Q. Selection of charge methods for lithium ion batteries by considering diffusion induced stress and charge time., 2016, 320: 104–110.

[44] ZHAO Y F, LÜ B. Stress evolution induced by charging shut-down in lithium-ion batteries., 2018, 40(1): 77–82.

[45] KIM S, HUANG H Y S. Mechanical stresses at the cathode– electrolyte interface in lithium-ion batteries., 2016, 31(22): 3506–3512.

[46] JI L, GUO Z S. Analytical modeling and simulation of porous electrodes: Li-ion distribution and diffusion-induced stress., 2018, 34(1): 187–198.

[47] JI L, GUO Z S, WU Y J. Computational and experimental observation of Li-ion concentration distribution and diffusion-induced stress in porous battery electrodes.., 2017, 5(9): 1702–1711.

[48] DIMITRIJEVIC B J, AIFANTIS K E, HACKL K. The influence of particle size and spacing on the fragmentation of nanocomposite anodes for Li batteries, 2012, 206: 343–348.

[49] XU R, ZHAO K J. Mechanical interactions regulated kinetics and morphology of composite electrodes in Li-ion batteries., 2016, 8: 13–21.

[50] MAI W J, YANG M, SOGHRATI S. A particle-resolved 3D finite element model to study the effect of cathode microstructure on the behavior of lithium ion batteries., 2019, 294: 192–209.

[51] RENGANATHAN S, SIKHA G, SANTHANAGOPALAN S,. Theoretical analysis of stresses in a lithium ion cell., 2010, 157(2): A155–A163.

[52] RAHANI E K, SHENOY V B. Role of plastic deformation of binder on stress evolution during charging and discharging in lithium- ion battery negative electrodes., 2013 160(8): A1153–A1162.

[53] MENDOZA H, ROBERTS S A, BRUNINI V E,. Mechanical and electrochemical response of a LiCoO2cathode using reconstructed microstructures., 2016, 190: 1–15.

[54] WU L M, XIAO X H, WEN Y H,. Three-dimensional finite element study on stress generation in synchrotron X-ray tomography reconstructed nickel-manganese-cobalt based half cell., 2016, 336: 8–18.

[55] QI H R, FENG L, WANG S B,. Stress relaxation through electrochemical diffusion in electrodes.(), 2016, 46(8): 1–15.

[56] LIU M. Finite element analysis of lithium insertion-induced expansion of a silicon thin film on a rigid substrate under potentiostatic operation., 2015, 275: 760–768.

[57] GAO Y F, ZHOU M. Coupled mechano-diffusional driving forces for fracture in electrode materials., 2013, 230: 176–193.

[58] CHEN B B, ZHOU J Q, ZHU J W,. Diffusion induced stress and the distribution of dislocations in a nanostructured thin film electrode during lithiation., 2014, 4(109): 64216–64224.

[59] WU B, LU W. A battery model that fully couples mechanics and electrochemistry at both particle and electrode levels by incorporation of particle interaction., 2017, 360: 360–372.

[60] ZHANG J Q, LÜ B, SONG Y C. A review of fracture in lithium- ion battery electrodes., 2017, 38(1): 18–37.

[61] JI L, GUO Z S, DU S Y,. Stress induced by diffusion, curvature, and reversible electrochemical reaction in bilayer lithium-ion battery electrode plates., 2017, 134: 599–609.

[62] SONG X, LU Y J, SHI M L,. Effects of plastic deformation in current collector on lithium diffusion and stress in bilayer lithium- ion battery electrode., 2018, 67(14): 1–9.

[63] SONG Y C, LI Z Z, ZHANG J Q. Reducing diffusion induced stress in planar electrodes by plastic shakedown and cyclic plasticity of current collector., 2014, 263: 22–28.

[64] LIU M, GAO C H, YANG F Q. Analysis of diffusion-induced delamination of an elastic-perfectly plastic film on a deformable substrate under potentiostatic operation., 2017, 25(6): 065019.

[65] LIU D Y, CHEN W Q, SHEN X D. Diffusion-induced stresses in an imperfect bilayer electrode of coin-shaped lithium-ion batteries., 2016, 55: 167–180.

[66] HAO F, FANG D N. Reducing diffusion-induced stresses of electrode– collector bilayer in lithium-ion battery by pre-strain., 2013, 242: 415–420.

[67] SONG Y C, LI Z Z, SOH A K,. Diffusion of lithium ions and diffusion-induced stresses in a phase separating electrode under galvanostatic and potentiostatic operations: phase field simulations., 2015, 91: 363–371.

[68] LI Y, ZHANG J, ZHANG K,. A defect-based viscoplastic model for large-deformed thin film electrode of lithium-ion battery., 2019, 115: 293–306.

[69] HE Y L, HU H J, SONG Y C,. Effects of concentration- dependent elastic modulus on the diffusion of lithium ions and diffusion induced stress in layered battery electrodes., 2014, 248: 517–523.

[70] LIU D Y, CHEN W Q, SHEN X D. Diffusion-induced stresses in graphene-based composite bilayer electrode of lithium-ion battery., 2017, 165: 91–98.

[71] ZHANG X Y, HAO F, CHEN H S,. Diffusion-induced stress and delamination of layered electrode plates with composition- gradient., 2015, 91: 351–362.

[72] LU B, SONG Y C, GUO Z S,. Modeling of progressive delamination in a thin film driven by diffusion-induced stresses., 2013, 50(14/15): 2495–2507.

[73] PAL S, DAMLE S S, KUMTA P N,. Modeling of lithium segregation induced delamination of a-Si thin film anode in Li-ion batteries., 2013, 79: 877–887.

[74] HAFTBARADARAN H, XIAO X C, VERBRUGGE M W,. Method to deduce the critical size for interfacial delamination of patterned electrode structures and application to lithiation of thin-film silicon islands., 2012, 206: 357–366.

[75] YANG L, CHEN H S, SONG W L,.optical observations and simulations on defect induced failure of silicon island anodes., 2018, 405: 101–105.

[76] CHEN D, KRAMER D, MÖNIG R. Chemomechanical fatigue of LiMn1.95Al0.05O4electrodes for lithium-ion batteries., 2018, 259: 939–948.

[77] XU R, YANG Y, YIN F,. Heterogeneous damage in Li-ion batteries: experimental analysis and theoretical modeling., 2019, 129: 160–183.

[78] YIM T, CHOI S J, JO Y N,. Effect of binder properties on electrochemical performance for silicon-graphite anode: method and application of binder screening., 2014, 136: 112–120.

[79] LI C L, SUN Q, JIANG J Y,. Electrochemistry and morphology evolution of carbon micro-net films for rechargeable lithium ion batteries., 2008, 112: 13782–13788.

[80] LI J C, DOZIER A K, LI Y C,. Crack pattern formation in thin film lithium-ion battery electrodes., 2011, 158(6): A689–A694.

[81] ZHANG J Z, ZHANG J, WANG D,. Stress evolution in SiO electrodes for lithium-ion batteries during electrochemical cycling., 2017, 190: 79–82.

[82] QU F, LI C L, WANG Z M,. Eutectic nano-droplet template injection into bulk silicon to construct porous frameworks with concomitant conformal coating as anodes for Li-ion batteries., 2015, 5: 10381.

[83] QU F, LI C L, WANG Z M,. Metal-induced crystallization of highly corrugated silicon thick films as potential anodes for Li-ion batteries., 2014, 6: 8782–8788.

[84] ZHANG Z A, ZENG T, LAI Y Q,. A comparative study of different binders and their effects on electrochemical properties of LiMn2O4cathode in lithium ion batteries., 2014, 247: 1–8.

[85] SETHURAMAN V A, WINKLE N V, ABRAHAM D P,. Real-time stress measurements in lithium-ion battery negative- electrodes., 2012, 206: 334–342.

[86] PHARR M, CHOI Y S, LEE D W,. Measurements of stress and fracture in germanium electrodes of lithium-ion batteries during electrochemical lithiation and delithiation., 2016, 304: 164–169.

[87] SUTHAR B, NORTHROP P W C, RIFE D,. Effect of porosity, thickness and tortuosity on capacity fade of anode., 2015, 162(9): A1708–A1717.

[88] YANG X G, BAUER C, WANG C Y. Sinusoidal current and stress evolutions in lithium-ion batteries., 2016, 327: 414–422.

[89] WU W, XIAO X R, WANG M,. A microstructural resolved model for the stress analysis of lithium-ion batteries., 2014, 161(5): A803–A813.

[90] RIEGER B, ERHARD S V, KOSCH S,. Multi-dimensional modeling of the influence of cell design on temperature, displacement and stress inhomogeneity in large-format lithium-ion cells., 2016, 163(14): A3099–A3110.

[91] RIEGER B, SCHUSTER S F, ERHARD S V,. Multi-directional laser scanning as innovative method to detect local cell damage during fast charging of lithium-ion cells., 2016, 8: 1–5.

[92] ZHANG L J, CHENG H Z, MENG D J. Experiment study on ETSS coupling mechanism and identification of key parameter for lithium-ion batteries., 2017, 51(8): 142–148.

[93] YU C C, DAI H F. The stress measurement and analysis of the lithium-ion battery., 2015, 21(8): 14–17, 32.

[94] SAUERTEIG D, HANSELMANN N, ARZBERGER A,. Electrochemical-mechanical coupled modeling and parameterization of swelling and ionic transport in lithium-ion batteries., 2018, 378: 235–247.

[95] BARAI A, TANGIRALA R, UDDIN K,. The effect of external compressive loads on the cycle lifetime of lithium-ion pouch cells., 2017, 13: 211–219.

[96] CANNARELLA J, ARNOLD C B. Stress evolution and capacity fade in constrained lithium-ion pouch cells., 2014, 245: 745–751.

[97] WÜNSCH M, KAUFMAN J, SAUER D U. Investigation of the influence of different bracing of automotive pouch cells on cyclic lifetime and impedance spectra., 2019, 21: 149–155.

[98] LI R H, REN D S, GUO D X,. Volume deformation of large-format lithium ion batteries under different degradation paths., 2019, 166(16): A4106–A4114.

[99] MUSSA A S, KLETT M, LINDBERGH G,. Effects of external pressure on the performance and ageing of single-layer lithium- ion pouch cells., 2018, 385: 18–26.

[100] ZHANG J, HAN X, HU C J,. An optimization of the pressing force applied onto the module structure of soft-package lithium-ion battery., 2016, 38(6): 669–673+715.

[101] PFRANG A, KERSYS A, KRISTON A,. Long-term cycling induced jelly roll deformation in commercial 18650 cells., 2018, 392: 168–175.

[102] SCHUSTER S F, BACH T, FLEDER E,. Nonlinear aging characteristics of lithium-ion cells under different operational conditions., 2015, 1: 44–53.

[103] BACH T C, SCHUSTER S F, FLEDER E,. Nonlinear aging of cylindrical lithium-ion cells linked to heterogeneous compression., 2016, 5: 212–223.

Progress on Failure Mechanism of Lithium Ion Battery Caused by Diffusion Induced Stress

WANG Yanan1,2,3, LI Hua1,2,3, WANG Zhengkun1, LI Qingfeng1, LIAN Chen1, HE Xin1

(1. School of Mechanical Engineering, Shandong University, Jinan 250061, China; 2. Key Laboratory of High-Efficiency and Clean Mechanical Manufacture of Ministry of Education, Shandong University, Jinan 250061, China; 3. National Demonstration Center for Experimental Mechanical Engineering Education, Shandong University, Jinan 250061, China)

During charge and discharge of lithium-ion battery, the concentration gradient produced by lithium- ion diffusion process and deformation caused by lithiation expansion of the active material result in diffusion-induced stress. Excessive diffusion-induced stress can cause various mechanical failure modes such as cracking of active particles, separation between active particles, fracture of active layers, and delamination between active layers and current collectors, which eventually leads to a series of failure phenomena such as capacity attenuation, impedance rise and cycle life loss of the battery. Therefore, the diffusion-induced stress and the derived failure mechanism of lithium-ion battery become one of the research hotspots in the field of lithium-ion batteries, which has important theoretical and practical value. In this paper, research progress of the failure mechanism of lithium-ion battery caused by diffusion-induced stress in recent years is reviewed from different levels of the active particle, the active electrode, the half-cell, the cell unit, and the cell. The generation mechanism and research methods of diffusion-induced stress are introduced. The influence of diffusion-induced stress on the mechanical and electrochemical properties of the battery is analyzed, and the influencing factors of the diffusion-induced stress are summarized. Finally, the future research directions and development trends are prospected.

lithium-ion battery; diffusion-induced stress; failure mechanism; multiphysics coupling model; review

TM912

A

1000-324X(2020)10-1071-17

10.15541/jim20190622

2019-12-06;

2020-02-27

国家自然科学基金(51405269); 汽车仿真与控制国家重点实验室基金(20181102)National Natural Science Foundation of China (51405269); Foundation of State Key Laboratory of Automotive Simulation and Control (20181102)

王亚楠(1981–), 男, 博士, 讲师. E-mail: wyn@sdu.edu.cnWANG Yanan(1981–), male, PhD, lecturer. E-mail: wyn@sdu.edu.cn