基于混合方向性距离函数的长三角地区碳排放绩效评价

（合肥工业大学管理学院，合肥 230009）

引 言

联合国发布的 《2019年可持续发展目标报告》指出，气候变化以及发展不平等问题是当今世界面临的两大主要挑战。2019年11月22日，气候变化绿皮书 《应对气候变化报告2019：防范气候风险》指出，2018年全球平均温度较工业化前水平高出1℃。中国作为负责任的大国，在面对减排压力时，要双手同时抓经济发展和碳减排。为了实现双赢，对碳排放绩效进行评价有助于碳减排工作的展开，符合可持续发展目标。习近平总书记提出支持长江三角洲区域一体化发展并上升为国家战略，着力落实新发展理念。因此，对长三角地区碳排放绩效进行评价有利于其更好地发展低碳经济。

碳排放绩效衡量指标经历了单要素到多要素两个发展阶段。最初，大多数学者利用单要素指标来评价碳排放绩效， 如Mielnik和Goldemberg José[1]、Sun[2]、 Ang 和 Liu[3]分别提出 “碳指数” 即单位能源碳排放量、单位GDP碳排放量和能源强度即单位GDP的能源消耗量。单要素评价指标简单易懂，但是由于忽略了其他投入要素而无法对决策单元进行全面合理的评价。Ramanathan[4]提出了全要素思想，认为要结合所有投入要素、能源消耗和碳排放分析碳排放绩效。Zhou等[5]基于非径向方向性距离函数，提出碳排放绩效指数为潜在碳排放强度与实际碳排放强度的比值，Zhang和Choik[6]将其定义为全要素碳排放性绩效（TCPI）。

在生产过程中，非期望产出通常会伴随着期望产出而产生。在对经济发展进行评价时，考虑非期望产出有助于更好实现可持续发展目标。Ca⁃ves等[7]在进行绩效评价时忽略了非期望产出，Pittman[8]在其基础上进行了改进，将非期望产出纳入绩效评价分析框架。本文研究碳排放绩效评价，主要考虑的非期望产出是二氧化碳排放量。目前，碳排放绩效评价方法主要包括随机前沿分析法（SFA）和数据包络分析法（DEA）。DEA相对于SFA更加简便广泛，因为DEA不需要预先设定生产函数就可以得出结果，而且DEA更适用于多投入多产出的效率评价。DEA常与方向性距离函数结合进行绩效评价。CCR和BCC模型是DEA中传统的两种径向分析模型。Chung[9]在Shephard提出的产出距离函数基础上提出了能够同时降低非期望产出并增加期望产出的方向性距离函数DDF，并结合径向DEA计算决策单元的效率得分。在DEA发展进程中，非径向DEA测算逐渐兴起，如SBM模型。 Fukuyama和 Weber[10]指出存在非零松弛时，径向效率测算方法会高估效率值，Zhang等[11]指出径向DDF因未考虑松弛偏差而高估效率值。Zhou等[5]运用非径向方向性距离（NDDF）函数测算了有无热电联厂的能源绩效和碳排放绩效。Zhang等[11]提出全要素非径向距离函数（TN⁃DDF）和能源环境非径向距离函数，并定义测算全效率的指标和能源环境绩效指标。王兵和侯冰清[12]运用全局非径向方向性距离函数测算了中国30个省市的全要素绿色效率和全要素绿色生产率。Tone[13]指出径向测算方法忽视了投入产出的非径向松弛，非径向测算方法虽然处理了松弛问题但是忽视了投入产出的径向特征，从而提出径向测算方法与非径向测算方法的联合分析框架——混合测算方法，将投入和产出细分为径向部分和非径向部分。国内学者陈黎明等[14]、杨皓然和吴群[15]运用混合测算方法测算生态效率，杨皓然的研究结果显示混合方向性距离函数下的效率得分介于径向测算与非径向测算效率得分之间。

Oh等[16]基于全局方向性距离函数测算了46个国家的碳排放绩效。李涛和傅强[17]、马大来等[18]、 王群伟等[19]分别利用不同的方法测算了中国不同省市层面的碳排放绩效。曲晨瑶等[20]利用超效率DEA模型分析了中国制造业不同行业的碳排放效率及其影响因素，得出碳排放效率影响因素具有行业异质性。向鹏成和张棚[21]、高鸣和宋洪远[22]、 王喜平和刘兴会[23]分别对中国建筑业、农业和电力行业的碳排放绩效进行了分析研究。

现有大多数学者采用的径向测算方法因未考虑松弛偏差而高估效率值，非径向测算方法因忽视了投入产出的径向特征而可能低估效率值，采用HDDF测算的结果会更准确。目前已有的大多数碳排放绩效研究都是基于国家或者省级层面，而区域碳排放绩效评价研究较少。因此，本文运用非角度的HDDF对长三角地区的全要素碳排放绩效进行分析，并且进一步考虑到样本的时间动态和组间异质性，探讨中心区城市和非中心区城市在组技术前沿和全局技术前沿的绩效水平，以期为长三角地区成为绿色低碳的未来城市并实现更高质量一体化发展提供科学依据。

1 研究模型

1.1 研究方法

1.1.1 方向性距离函数

本文综合Tone[13]提出的效率混合测度和方向性距离函数，构建混合方向性距离函数模型测算碳排放绩效。假设有N个决策单元（DMUn，n＝1，2，…，N）， 每个决策单元有M项投入（Xmn，m＝1，2，…，M），H项期望产出S项非期望产出。 混合效率测度方法下，需要将投入、期望产出和非期望产出拆分成径向和非径向两部分。M项投入拆分为m1项径向投入、m2项非径向投入。即投入矩阵X分解为径向投入部分和非径向投入部分，即Xmn＝（XR，XNR），其中m＝m1＋m2。期望产出分解为径向期望产出部分和非径向期望产出部分，即Yd＝（YRd，YNRd），其中h＝h1＋h2。非期望产出分解为径向非期望产出部分和非径向非期望产出部分即Yu＝（URu，YNRu）T， 其中s＝s1＋s2。 方向向量分解为径向部分和非径向部分：g＝（gR，gNR，gRd，gNRd，gRu，gNRu）。

通过计算式（1）求解混合方向性距离函数：

Oh[16]、 Zhang 和 Choi[6]考虑了研究样本的时间动态和组间异质性，构建了3种环境生产技术，分别为同期环境生产技术、跨期环境生产技术和全局环境生产技术，分别用符号TC、TI、TG来表示。同期环境生产技术针对同一组样本在某一时期t的技术状况，跨期生产技术针对同一组样本在整个样本时期内的技术状况，全局生产技术针对所有样本组在整个时期的技术状况。3种环境生产技术对应3种类别的技术前沿，DMU0在3种情况下的效率得分也不同，其对应的混合方向性距离函数分别表示为

1.1.2 全要素碳排放绩效

基于Zhou等[5]对碳排放绩效的定义，碳排放绩效是潜在碳排放强度与实际碳排放强度的比值，通过式（2）测算全要素碳排放绩效：

基于前述的3种环境生产技术，可以计算出3种静态碳排放绩效，即同期碳排放绩效（TCPIC）、跨期碳排放绩效（TCPII）和全局碳排放绩效（TCPIG）。TCPI的值越大，说明DMU0的效率越高，等于1时，表明DMU0是相对有效的。

1.1.3 全要素碳排放绩效的动态变化及其分解

根据 Oh[16]、 Zhang 和 Choi[6]的方法， 通过式（3）计算指数MHMCPI，以反映碳排放绩效动态变化。考虑到时间动态和组间异质性，本文将MH⁃MCPI指数分解为3个部分，见式（3）：第1部分是效率变化（EC），衡量DMU0在t＋1时期和t时期对同期环境技术前沿追赶的比例；第2部分是最佳实践差距变化，是DMU0在t＋1时期和t时期的同期环境技术前沿对跨期环境技术前沿追赶的比例；第3部分是技术差距变化效率，是DMU0在t＋1和t时期跨期环境技术前沿对全局环境技术前沿追赶的比例。

1.2 变量选取与样本数据来源

1.2.1 投入变量

参照多数学者的研究，本文选择能源指标和非能源指标两类指标作为投入变量。非能源指标包括资本存量和劳动力，能源指标指能源消耗量。

资本（K）：向娟[24]运用永续盘存法计算出中国各城市2009年的固定资本存量，刘常青等[25]根据向娟的研究方法计算出2014年中国地级以上城市的资本存量。本文在二者的研究基础上运用永续盘存法计算出长三角地区各地级市2014～2018年的资本存量数据。

劳动力（L）：本文根据各城市统计年鉴中的从业人员数，将年初与年末从业人员的平均数作为劳动力指标。

能源（E）：能源数据来源于各城市统计年鉴中的综合能源消费量。

1.2.2 产出变量

本文选择地区生产总值（GRP）和工业生产总值（GIP）作为期望产出，选择二氧化碳排放量（C）作为非期望产出。地区生产总值和工业生产总值数据来源于各城市统计年鉴。二氧化碳排放量数据无法从统计年鉴中直接获取，需要经过计算获得。根据程豪[26]介绍的 《2006年IPCC国家温室气体清单指南》，可以根据式（4）计算出二氧化碳排放量。

其中能源消耗量数据来源于各城市统计年鉴，本文选取原煤、焦炭、原油、汽油、煤油、柴油、燃料油、液化石油气和天然气消耗量作为能源消耗指标，并根据指南中提供的各能源的二氧化碳排放系数，运用公式计算出各城市的二氧化碳排放量指标。

1.2.3 样本数据来源

本文以长三角地区各地级市作为研究对象。长三角区域一体化发展规划中明确以27个城市为中心区，辐射带动整个长三角高质量发展。鉴于中心城市和非中心城市在经济发展水平等方面的区别，本文将长三角各城市划分为中心区城市和非中心区城市两组。这种处理方法可以将中心区城市与非中心区城市的碳排放绩效进行对比，计算所得的组前沿下的绩效水平更加公平。由于部分城市在样本期间的数据存在缺失，故剔除数据缺失的几个城市，以剩余33个城市投入、产出的平衡面板数据分析研究碳排放绩效情况。本文数据来源于 《中国统计年鉴》、《中国区域经济统计年鉴》、《能源统计年鉴》以及各城市统计年鉴。

1.3 确定径向变量和非径向变量

基于HDDF的要求，首先需要确定投入、产出变量中的径向变量和非径向变量。Chiu等[27]运用Spearman相关系数检验确定，认为相关系数超过0.76的两个变量相关性强，应该作为径向变量；否则，作为非径向向量。

从表1可知，3个投入变量之间的Spearman相关系数均小于0.76，因此3个投入变量均为非径向投入变量；地区生产总值与工业生产总值之间的Spearman相关系数大于0.76，因此地区生产总值与工业生产总值作为径向产出变量，二氧化碳排放量作为非径向产出变量。

表1 斯皮尔曼相关系数检验

2 碳排放绩效及其动态变化测算结果与讨论

2.1 全局碳排放绩效测算结果

本文利用软件MAXDEA ULTRAL7.11测算了2014～2018年长三角地区33个城市的碳排放绩效，包括TCPIC、TCPII和TCPIG。TCPIG的测算结果如表2所示，（1）从两个组别的绩效平均值可以看出，在2014～2018年间，中心区城市绩效均值均高于非中心区城市的均值，表明前者的碳排放绩效水平总体上优于后者；（2）分别从两个组内部碳排放绩效可以得到，组1中心区的24个城市中，上海、无锡和苏州2014～2018年碳排放绩效均高于0.9，均值分别为0.9284、0.9759和0.9673，其中碳排放绩效最好的是无锡市。中心区城市中多数城市的碳排放绩效均值处于0.5～0.8区间水平，包括常州、南通、扬州等14个城市。南京、舟山、铜陵、安庆、滁州、池州和宣城的碳排放绩效均不足0.5，处于相对较低水平。组2非中心区的9个城市中，宿迁和黄山2014～2018年碳排放绩效相对较高，其他7个城市的碳排放绩效均值均不足0.5； （3）从省市层面差异可得，上海市、江苏省、浙江省、安徽省的碳排放绩效均值依次递减，安徽省的碳排放绩效最差。江苏省的无锡和苏州碳排放绩效相对较好，南京的碳排放绩效最差，这与徐国泉和栾昊[28]的研究结果一致。浙江省的杭州、宁波和绍兴碳排放绩效相对较好，舟山碳排放绩效最差，每年的绩效均值均在0.3左右。安徽省的芜湖和黄山碳排放绩效相对较好，其他地区碳排放绩效多数低于0.5，其中池州市碳排放绩效最差，均值只有0.1995。

表2 2014～2018年长三角地区33个城市TCPIG测算结果

续 表

2.2 碳排放绩效的动态变化

以（1，1）为中心将图1区域划分为4个象限。右上角区域为第一象限，位于第一象限的点EC与EPC均大于1，称为 “双高型”区域，位于该区域的城市可以作为其他城市改善碳排放绩效的标杆。样本期间内随着时间推移，位于该象限城市的实际生产在向同期生产前沿面靠近，效率在逐步提高；同时当期技术前沿在向跨期技术前沿靠近，实际最优生产技术在向潜在最优生产技术追赶，生产技术水平在进步。图1结果显示，位于第一象限的城市包括上海、苏州、合肥、宁波等，其中大多数城市隶属于江苏省。

左上角区域为第二象限，位于该象限的城市EC小于1而BPC大于1，这些地区的实际生产逐渐远离同期生产前沿面，效率在退步，但同时生产技术水平在进步，如温州、淮南、安庆等。该象限城市应该着重提高效率水平，将技术高效应用到减排上去。研究对象中大多数城市都位于第二象限，其中城市主要隶属于安徽省。

左下角区域为第三象限，位于第三象限的城市EC小于1且BPC小于1，称为 “双低型”区域。这些地区在样本期间效率水平和技术水平都在逐渐退步，如芜湖、台州等城市。位于此区域的城市应特别引起重视，无论是效率方面还是生产技术方面，都应该采取措施加以改进，防止碳排放绩效持续恶化。

右下角区域为第四象限，位于第四象限的点EC大于1而BPC小于1。位于该象限的城市效率水平逐渐提高，但是生产技术水平在逐渐退步，如绍兴等。

图1结果显示，绝大多数城市BPC位于第一、二象限，BPC大于1，表明生产技术进步是驱动长三角地区碳排放绩效提高的主导因素，技术创新是长三角地区实现低碳经济的重要环节。此外，安徽省和浙江省的大多数城市存在效率低下问题；与中心区相比，非中心区城市多位于图1左侧，表明非中心区的技术效率在退步，这些区域需要通过提高管理效率和资源配置效率来改善碳排放绩效。

图1 2014～2018年EC与EPC均值分布散点图

图2结果显示，中心区在样本期间内TGC恒为1，非中心区恒大于1，表明中心区城市始终处于长三角地区环境生产技术的制高点，引领长三角地区发展低碳经济；而非中心区城市的低碳经济发展状况虽然落后于中心城市，但在样本期间向中心区城市追赶。非中心区城市在未来应该保持良好势头，在中心区的引领下提高碳排放绩效。

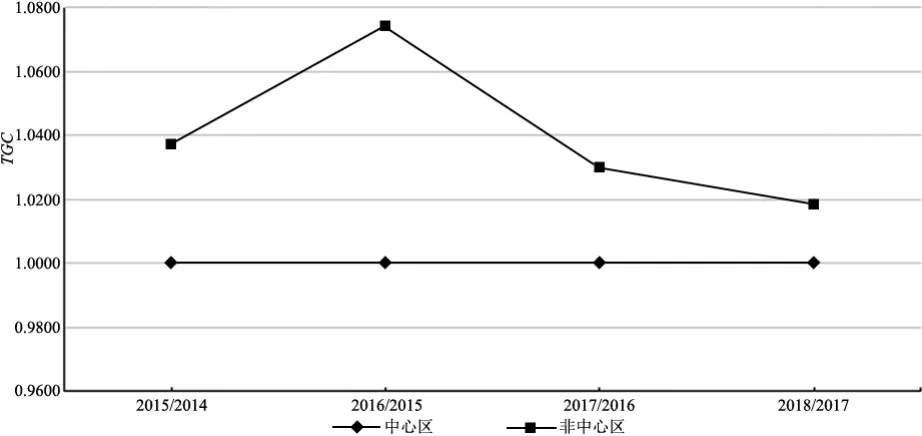
图2 2014～2018年TGC变化趋势

图3展示了江苏、浙江、安徽3省内各地级市的MHMCPI、EC和EPC四分位图。江苏省的低碳经济发展状况最好，浙江省次之，安徽省最差。江苏省碳排放绩效总体发展态势向好，这源于效率的改善和生产技术的进步。此外，江苏省碳排放绩效内部差异最小，发展相对更加均衡，浙江省内部差异相对更大。安徽省内部差异大，尤其是EC不仅小于1且分散，表明安徽省效率退步，且各城市效率水平差异大。总体来看，3个地区的环境生产技术都在进步，技术进步是推动长三角地区发展低碳经济的驱动力。

图3 江浙皖内部地级市MHMCPI、EC、EPC四分位图

3 结 论

研究发现，长三角地区24个中心区城市的碳排放绩效总体上优于非中心区城市，且前者的环境生产技术始终领先于后者。非中心区城市应当以中心区城市为前进目标，引领自身优化环境生产技术，进而改善碳排放绩效。位于中心区的上海、无锡和苏州碳排放绩效最优，位于非中心区的黄山碳排放绩效相对较优。这些低碳经济发展相对较好的城市应当继续发挥自身在技术创新和管理效率方面的优势，并进一步提高碳排放绩效水平，带领其他地区共同发展。

内部低碳经济发展不平衡是长三角地区存在的一个问题。各个省份之间差异明显，而且各省内差异也较大，低碳经济发展状况极不平衡。上海、无锡和苏州碳排放绩效水平较高，绩效值高于0.9；而南京、舟山、池州和宣城等城市相对较低，不足0.5甚至更低。上海、江苏、浙江、安徽的碳排放绩效平均水平依次降低，同时其内部差异程度也依次扩大。因此，长三角地区应当促进内部协同发展，减小碳排放绩效的内部差异。

效率恶化是制约长三角地区碳排放绩效提高的一个主要原因。技术进步促进长三角地区提高碳排放绩效，而效率恶化抑制了绩效的改善。无论是中心区城市还是非中心区城市，在环境生产技术方面始终在进步。但大部分城市的效率恶化效应超过了技术进步效应，导致碳排放绩效不升反降，尤其是安徽省效率恶化问题最严重，且内部差异很大。

合肥、宁波、杭州等地区在样本期间内无论是在技术创新还是管理效率方面都积极向好，表明其未来提高碳排放绩效的潜力较大；而台州、芜湖等地区在样本期间内既存在技术退步又存在效率恶化，应该着力弄清问题所在，并采取措施积极应对，以防最终导致其碳排放绩效的大大降低。