基于MQ-RBF-FD求解对流扩散方程的二阶算法

姚林，唐泉

(新疆师范大学 数学科学学院，新疆 乌鲁木齐 830017)

对流扩散方程能够模拟许多物理、化学、经济和金融的现象从而进行预判，对其数值解的研究由来已久，已有的数值方法包括有限差分(FD)[1]、有限元(FE)[2]和边界元方法[3]等。一般采用局部插值格式[4]进行推导，需要一个网格来支持操作。对流扩散方程的特点是包括一阶导数的对流项和二阶导数的扩散项，对于网格的选择要求很严格，如果选择的网格结构不合适，数值逼近将会产生迎风效应和数值扩散。径向基函数(RBF-FD)方法[5]是一种局部有效的无网格方法，广泛用于求解多尺度和偏微分方程等，解决了选择合适网格的困难，具有数值精度高、构造数值格式容易和程序操作简单等优点。因此，本文将基于RBF-FD方法的优点，构造出稳定和有效的数值格式，避免出现数值振荡和数值扩散。

本文主要研究对流扩散方程的数值逼近问题，考虑这类方程：

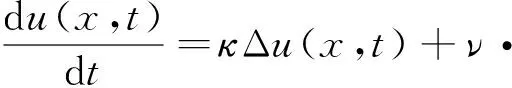
边界条件和初始条件为

其中，Ω是二维区域，t∈(0,T]，T是终止时间，κ=[κx,κy]T是扩散系数，ν=[νx,νy]T是对流系数，u=u(x,t)表示依赖时间t的函数，g(x,t)表示边界函数，u0(x)表示初始条件。

本文提出一种新颖的二阶离散格式求解对流扩散方程[6]。采用二次元局部的径向基函数(MQ-RBF-FD)方法进行空间离散[7]，时间分裂使用交替迭代算子分裂方法[8-9]，BDF2方法用于时间离散。首先，使用维数分裂格式把二维方程转化成沿X和Y方向的算子，梯度算子和拉普拉斯算子使用MQ-RBF-FD公式进行离散[10]，推导出空间二阶格式；其次，时间分裂采用交替迭代格式，可以有效减少分裂误差，迭代格式使用BDF2方法进行离散，目的是使时间格式上也达到二阶精度；最后，进一步测试出适当的迭代步数，目的是平衡时间和空间步长，再选取适合的形状参数c，最终使得数值解达到高阶精度。数值实验能够验证本文提出的二阶方法要大大优于FD方法。

1 空间二阶算法的推导过程

我们应用五点RBF-FD公式离散对流扩散方程中的梯度算子和拉普拉斯算子。采用维数分裂格式分裂二维对流扩散方程：

其中

(1)

同理

这里使用φi(x)替换上式中的u(x)

φi(x1)=ω1φ1(x1-h)+ω2φ2(x1)+ω3φ3(x1+h)，

(2)

Δφi(x1)=γ1φ1(x1-h)+γ2φ2(x1)+γ3φ3(x1+h)，

(3)

(4)

公式(4)表示MQ径向基函数，从式(2)和(3)中求出ωi,γi(i=0,1,2)，同理求出ωi,γi(i=0,3,4)[11-12]。Ax,Ay离散格式如下：

其中，h是空间步长，通过维数分裂，MQ-RBF-FD方法，简单技巧处理，即可在空间格式上获得二阶格式，相比于FD方法，精度更高。通过空间离散，二维对流扩散方程转化成常微分方程组，下面讨论时间分裂和时间离散方法。

2 时间分裂和离散的推导形式

时间分裂使用交替迭代格式[13]，时间离散采用BDF2方法。按照第1节处理方法，可以得到全离散格式：

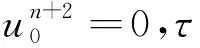
为达到二阶精度，我们需要找到最优迭代步数去平衡空间步长和时间步长。下面通过两个数值算例验证算法的合理性。

3 数值实验

3.1 数值实例1

算例1，我们考虑热传导方程：

这里u(x,y,t)属于温度函数，Ω=[0,1]×[0,1]，精确解：

uexact(x,y,t)=exp(-(κx+κy)π2t)sin(π(x+y))。

首先，通过数值实验选出最优形状参数c，我们选择扩散系数κx=κy=0.01，τ=h，T=1，迭代步数i=5。图1说明最优形状参数c在1附近，我们统一选择c=1。表1表示收敛阶和误差，说明MQ-RBF-FD方法优于FD方法。其次，选择扩散系数κx=0.1,κy=0.001,τ=h,T=1，形状参数c=1，迭代步数i=5。表2同样表示收敛阶和误差，说明扩散系数选取不同影响收敛阶和误差。

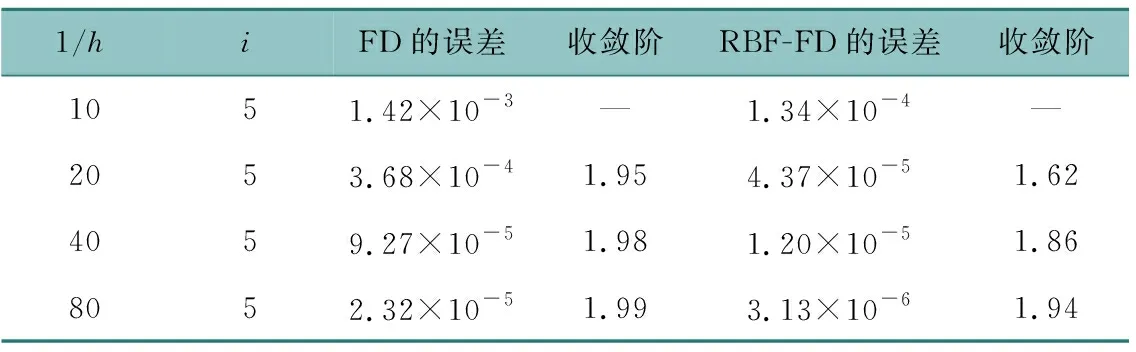
表1 RBF-FD方法和FD方法收敛阶和误差比较(κx=κy=0.01)Table 1 Convergence order and error comparison for RBF-FD and FD method(κx=κy=0.01)

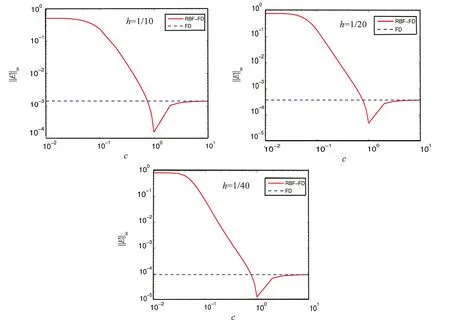
图1 不同的形状参数c之间的误差比较 Fig.1 Error comparison among different shape parameters

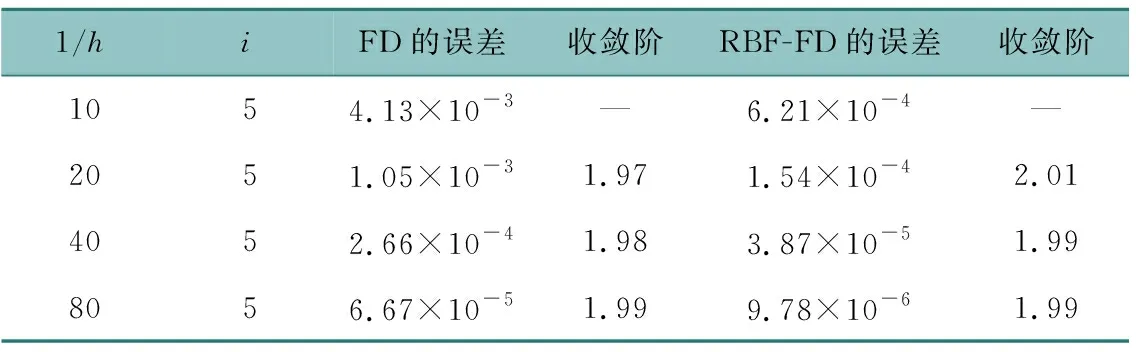
表2 RBF-FD方法和FD方法收敛阶和误差比较(κx=0.1，κy=0.001)Table 2 Convergence order and error comparison for RBF-FD and FD method(κx=0.1，κy=0.001)

3.2 数值实例2

算例2，我们考虑含有对流项的对流扩散方程：

解析解：

首先，我们选取扩散系数κx=κy=1，对流系数νx=νy=1，a=1,b=0.1,τ=0.5h,T=0.1，选取合适的迭代步数i=121，最优形状参数c=2，表3表示收敛阶和误差。其次，选取对流系数νx=νy=10，最优形状参数c=0.2，其他参数不变，表4表示收敛阶和误差。表3和表4比较说明对流系数不同，结果影响很大。最后，选取空间步长h=1/30，迭代步数i=261，其他参数与表3系数相同，得到数值解。图2表示数值解图和精确解图之间的比较。

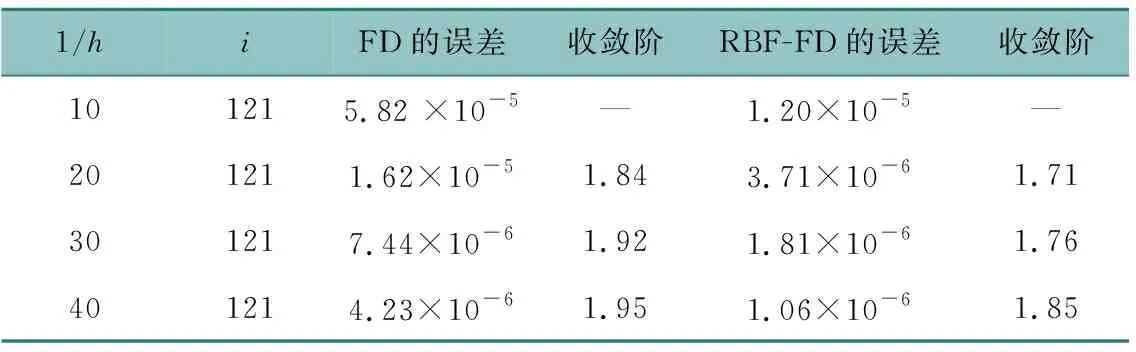
表3 RBF-FD方法和FD方法收敛阶和误差比较(υx=υy=1，c=2)Table 3 Convergence order and error comparison for RBF-FD and FD method(υx=υy=1，c=2)

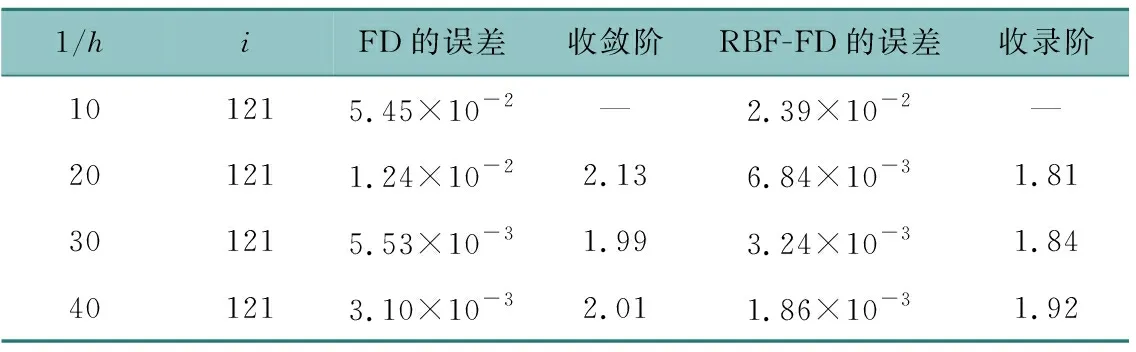
表4 RBF-FD方法和FD方法收敛阶和误差比较(υx=υy=10，c=0.2)Table 4 Convergence order and error comparison for RBF-FD and FD method(υx=υy=10，c=0.2)

4 结论

本文提出一种新颖的二阶算法求解对流扩散方程，着重描述了二阶算法的推导过程以及时间离散的推导形式，阐述了维数分裂和交替迭代格式在处理对流扩散方程中的优势，说明了迭代步数在平衡时间和空间步长中的重要作用。数值算例印证了本文提出的二阶算法的合理性和可行性，且精度远远高于FD方法。将来我们会考虑给出二阶算法的理论证明。