钢筋混凝土悬索桥有限元分析

张文帅，杨毅

（1.安徽建筑大学研究生院，安徽 合肥 230000；2.安徽水安建设集团股份有限公司，安徽 合肥 230000）

1 理论分析

1.1 悬索桥简介

悬索桥是一种悬吊体系桥梁，又名吊桥，由桥塔、主缆、吊索、桥面等体系组成，主要承重结构是悬索，如图1。桥体自重和移动荷载等竖向荷载经吊索分配，根据吊索的刚度传至主缆，进一步传至锚墩，横向荷载由整体桥梁结构共同承受，受力的分配取决于刚度的大小[1]。由于悬索桥刚度较小，在移动荷载作用下，相对于其他结构的桥梁，会产生较大的变形，因此对悬索桥运行时的受力状态进行分析显得十分重要。

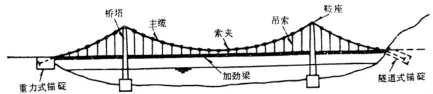
图1 悬索桥总体布置图

1.2 悬索桥理论发展[2]

1.2.1 传统的弹性理论

在十九世纪八十年代的欧洲，Navier和Castigliano尝试将拱结构的力学原理应用到对悬索桥的内力的分析，由此，悬索桥最初的弹性理论被人们所熟知。

用弹性理论计算时，应满足下列假设：

①吊索和主缆全部为柔性，吊索随跨密布；

②吊索弧线形状及坐标受外载后不发生变化；

③加劲梁截面特性保持不变；

根据上述三条假设可得到如下结果

水平力影响线：

其中：l—悬索桥跨度；lso—主缆长度；EC—主缆弹性模量；E—加劲梁弹性模量；

I—加劲梁惯性矩；Ac—主缆截面面积；Ψ1—主缆倾角；f—主缆垂度；

加劲梁剪力：Qx=Q0-tanΨ。

但由于传统弹性理论本质上忽略了变形对内力的影响，而事实上变形对内力是有一定影响，所以当悬索桥的跨度过大时，应采用挠度理论和有限位移理论进行计算更为准确。

1.2.2 挠度理论

挠度理论的假设与弹性理论大致相同，仅考虑主缆和吊索的变形对内力的影响。

图2 悬索桥挠度理论模型图

根据图2理论模型图可得到挠度理论的基本微分方程：

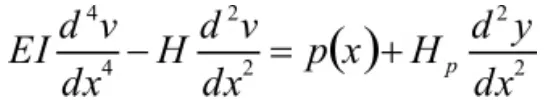
其中：E—弹性模量；I—惯性矩；Hp—活荷载荷载水平；Hg—恒荷载水平拉力；H=Hg+Hp

此理论受到长期广泛应用，但由于忽略了吊索以及加劲梁的非线性因素，准确度受到影响，由此有限元和有限位移理论逐渐兴起。

1.2.3 有限元和有限位移理论

随着计算机的快速发展，有限元和有限位移理论快速兴起。相对于上述弹性理论和挠度理论，有限元和有限位移理论在矩阵位移法的基础上充分地考虑了恒定荷载作用下的各种非线性因素的影响，此外，计算机对模型进行精确地分析计算，使有限元分析结果与现实的受力更符合，能够更快地对结构进行受力分析，保证结果的严谨性和准确性。

1.3 匀速常量力和匀速简谐力动力响应

1.3.1 匀速常量力作用

如图3所示，在作用在简支梁上常量力F从左向右匀速移动，忽略质量的影响，得到振动表达方程：，式中EI为抗弯刚度，m为质量。

图3 匀速常量力通过简支梁

振动的动力位移表达式：

将上述两式合并，再利用正交性可得到简化振动方程：

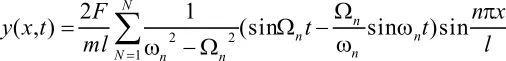
1.3.2 匀速简谐力作用

汽车因路面不平整产生的惯性力可当做一种简谐力，作用在简支梁上的简谐力从F1cosΩpt左向右匀速通过时，得到匀速简谐力动力响应的表达式：

式中ωn为固有频率，Ωp为扰动频率，Ωn为广义频率

2 工程概况

悬索桥主塔采用H型钢筋混凝土结构，C30混凝土，间距为120m，高度为54m，加劲梁为钢筋混凝土桁架，并在桥的两岸设置引桥，总体跨度为220m，主缆和吊索采用镀锌钢丝绳，垂跨比f/1=1/9，吊索共有52对，基本结构如下图4和图5。

图4 主桥的总体布置图（a）

图5 主桥的总体布置图（b）

3 数值分析

3.1 单元选择

为了准确地对悬索桥进行分析计算，建立有限元模型是不可或缺的一个重要部分，因此要针对悬索桥各个结构功能的不同，选用不同的有限元单元进行模拟，才能保证模型的准确性[3]。

图6 BEAM4单元几何

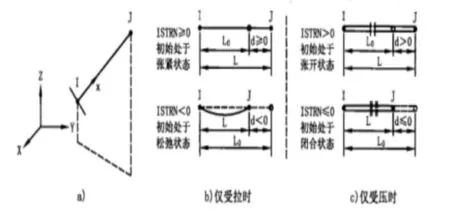
图7 LINK10单元几何

图8 SHELL63单元几何

材料参数表 表1

其中加劲桁架和桥塔使用BEAM4单元；主缆和吊索使用LINK10单元；桥面板模型使用SHELL63单元。各单元几何如图6～图8[4]。

3.2 悬索桥结构所用材料的力学参数

悬索桥使用的材料力学参数如表1。

图9 整体缆索塔柱模型

3.3 模型的建立

悬索桥有限元模型能否准确的建立，它对于结果分析有着举足轻重的作用，会对计算结果产生较大的影响，当悬索桥在恒定荷载作用下处于平衡状态，由于主缆受到桥体自身的重力荷载作用，主缆将受到的力传至锚墩，使得桥体处在受力均衡的平衡状态下，内力和外力之间的作用能够相互消除，从而桥体的各个结构都有初始应力，因此从这样的平衡状态下再进行下一步的分析比较合理且符合实际情况[5]；但当移动荷载作用于桥体时，初始的平衡状态不复存在，外力作用时，初始应力可以消除部分影响，在此失衡状态下结构必须通过建立新的协调方程达到另一个的平衡状态。

悬索桥结构在恒定荷载作用下的变形是不容忽视的，变形量是无法提前预料的，因此桥梁的结构刚度必须随着变形不断地进行变化，采用迭代的方法进行分析计算才能满足建立模型的要求，对于这种特殊要求，可以采用修正后的拉格朗日描述，即对于在时间内使结构产生变形的内力，均可用t时刻进行描述。

建立模型时，首先建立单侧缆索、塔柱模型，将模型对称复制到另一侧可得到整体缆索塔柱模型如图9，对桥面的建模采用自下而上的方法，得到桥面模型如图10。本例中悬索桥有限元模型相对来说比较简单，其中节点1159个，单元3273个。

对建立好的整体模型进行网格划分，分别对桥塔塔柱、塔柱之间的连接件进行划分如图11，在分别对主缆、桥塔塔基、加劲桁架两端施加边界条件，悬索桥的约束情况如图12。

图10 桥面模型

图11 有限元模型网格划分

图12 悬索桥约束情况

3.4 加载和求解

首先需要对主缆的初始应变进行不断调试，比较在不同初始应变的情况下跨中挠度是否最小且无限接近零，加劲桁架的结构部分最大轴力是否达到最小，以此来确定模型的初始位置。跨中挠度以及结构内力的最大值变化情况如下表2。

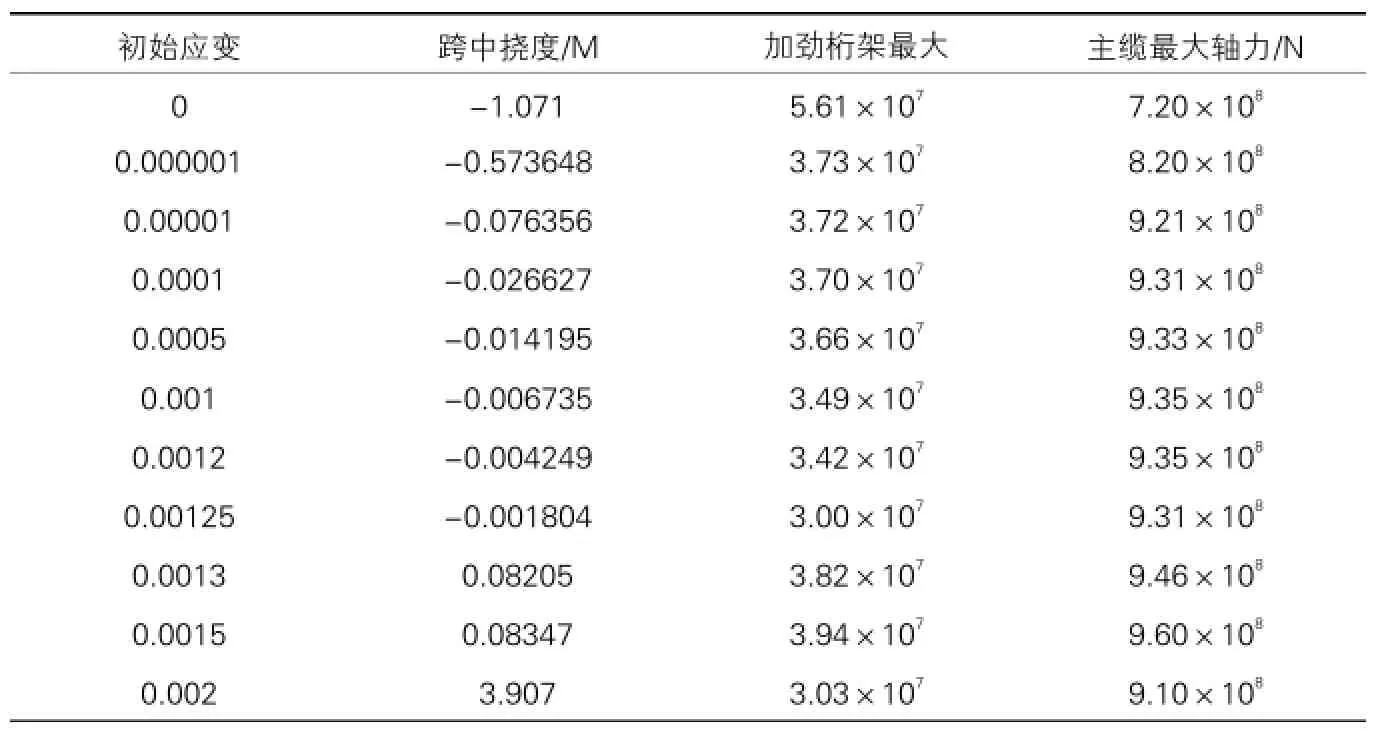
不同初应变下桥体跨中挠度和最大轴力 表2

结合表2和图13，可以看出桥梁挠度随着初始应变的增加而逐渐降低，当初始应变达到0.00125时，桥面的变形弯曲是最细微的；此外如图14轴力随着初始应变的增加而降低，达到极值点，此时初始应变为0.00125时，轴力最小，又随着初始应变的增加而逐渐增加，呈非线性，因此可以大体上确定，当初始应变为0.00125时，对此悬索桥进行有限元模拟分析可以满足实际工程的精度需求。

图13 桥梁挠度变化图

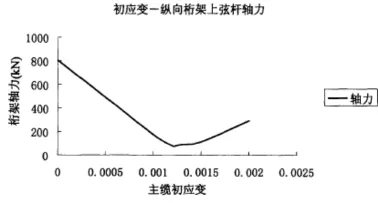
图14 上弦杆轴力变化图

在强迫振动问题中，在结构本身位置不变的情况下，对在挠动力作用下的强迫振动问题进行讨论，当结构的固定频率和挠动频率一致时，结构将会发生共振。所以强迫共振问题是必须要考虑到的。本例分别采用两种不同的情况进行分析：分别将移动荷载分为匀速常量力荷载和匀速简谐力荷载。其中荷载mg=2000N，假设车辆的四个车轮分别承担集中荷载，且数值相同，车轮距离设为6m，简谐力 F=500cos（10t），荷载速度为80km/h。

对荷载的移动速度、荷载经过一个单元所需时间、常量力的大小、简谐力的圆频率等进行参数定义，采用FULL的瞬态动力学分析法，且不能忽略重力对结果的影响，然后在车辆移动荷载的作用下对建立好的有限元模型加载求解。

3.5 结果后处理

在匀速常量力荷载的作用下，当荷载移动到跨中位置附近时，得到位移云图如图15，应力云图如图17，y向最大位移在距离桥塔最近的两根吊索的顶端，其值为0.060478m，最小位移在桥面的端部以及桥塔和桥面的交界处，其值为-0.001804m。桥体最大应力是4.46×106Pa，最小应力是61658Pa。

在匀速简谐力荷载的作用下，当荷载移动到跨中位置附近时，得到位移云图如图16，应力云图如图18，y向最大位移在距离桥塔最近的两根吊索的顶端，其值为0.060448m，最小位移在桥面的端部以及桥塔和桥面的交界处，其值为-0.001804m。桥体最大应力是4.48×106Pa，最小应力是62496Pa。

另外在结果后处理过程中，得到当移动荷载从桥上通过的过程中，桥上各个节点随荷载移动时竖向位移和速度的变化，在匀速常量力荷载作用下，得到各节点位移随时间变化图和速度随时间变化图，以跨中节点为例，如图19和图21，在在匀速简谐力荷载作用下，得到各节点位移随时间变化图和速度随时间变化图，以跨中节点为例，如图20和图22。

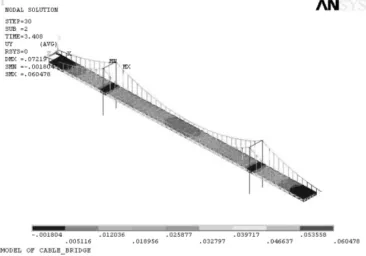
图15 匀速常量力荷载下桥梁y向位移云图

图16 匀速简谐力荷载下桥梁y向位移云图

图17 匀速常量力荷载下桥梁应力云图

图18 匀速简谐力荷载下桥梁应力云图

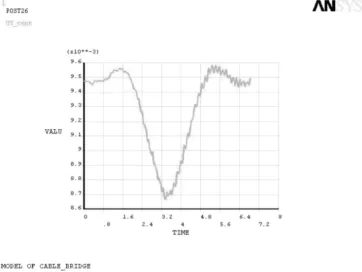
图19 跨中节点在匀速常量力作用下y向位移变化图

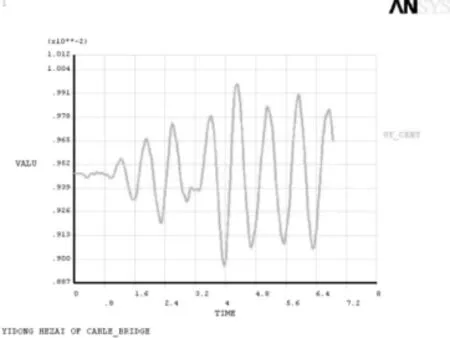
图20 跨中节点在匀速简谐力作用下y向位移变化图

在匀速常量力作用下，位移是从大到小再到大的过程，在移动荷载即将离开桥梁时，节点的y向位移是最大的，这相似于理论的分析结果。在匀速简谐力作用下，随着频率逐渐增大，当频率挨近桥梁的固有频率，可能会发生比较大的动态响应，使桥梁发生共振。

4 结论

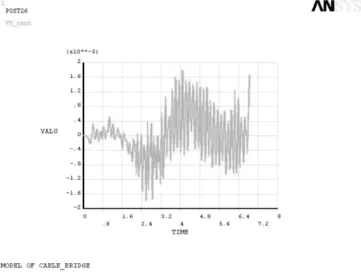
图21 跨中节点在匀速常量力作用下y向速度变化图

图22 跨中节点在匀速简谐力作用下y向速度变化图

通过上述的ANSYS数值模拟，对主缆的初始应变进行不断调试确定了初始位置，了解到钢筋混凝土悬索桥在匀速常量力和匀速简谐力下的位移的最大、最小值以及所处的位置和应力的分布情况，这让我们可以提前预测到荷载的最不利位置，为桥梁的正常运营、保证交通流畅提供了理论依据，是预防事故发生的根本保障，总之，ANSYS可以对比较复杂的结构进行数值模拟，计算结果和理论值误差较小，能够为实际工程提供指导性建议。