导弹垂直发射燃气排导系统两相流场数值分析

2020-11-02王俊敏邴笑寒

海军航空大学学报 2020年4期

王俊敏，邴笑寒，田琼，王楠

（1.91001部队，北京100089；2.92916部队，海南乐东372534；3.91375部队，北京102443）

导弹垂直发射系统具有通用性好、生命力强、全方位发射、发射率高等诸多优点[1-4]，被越来越多地应用于舰上。然而，导弹垂直发射的过程中将产生大量带有固体颗粒高速、高温燃气流，能否将燃气流顺利安全排出是实现导弹垂直发射的关键问题[5]。通过数值计算的方法对复杂的燃气流流场进行分析，可为燃气排导系统的安全防护以及优化设计等方面提供理论支撑。

目前，针对燃气流流场分析研究已经出现了大量成果。文献[6]分析了垂直发射装置内部流场结构，通过数值计算着重分析了排导系统被流场压强分布情况，总结了流场的激波结构特点。文献[7]给出了发射装置的物理模型，分析计算了导弹意外点火情况下的燃气排导系统承受的压强载荷。

文献[8]以舰载垂直发射系统燃气流场作为研究对象，分别给出了导弹点火后未动、导弹运动至发射箱1/4，1/2，3/4高度和导弹尾部刚出发射箱时等5种典型状态下的燃气流场分布规律。

然而，以上文献均只考虑了单纯的气相流场分布，忽略了颗粒相对流场分布的影响。本文以导弹垂直发射系统气固两相流场为研究对象，使用两相控制方程，采用“计算单元内颗粒源项算法”（PSIC）对两相流进行解耦计算，并利用FLUENT就导弹垂直发射高度和燃烧室压强对三维燃气流场参数分布的影响进行了着重分析，为下一步分析燃气排导系统损伤机理奠定基础。

1 模型建立

1.1 几何模型

导弹在发射的过程中，喷管尾部的气流流速远远大于导弹在发射箱内的移动速度。当导弹的运动位移较小时，可忽略其造成的流场变化；而当导弹运动位移增加时，燃气流对系统底部的压强将迅速减少。因此，可以将燃气排导系统内导弹发射起飞时的燃气流场用导弹在静止状态发射的流场简化，通过对导弹静态发射的流场计算来确定导弹发射时燃气排导系统受到的最严酷的载荷。燃气排导系统流场计算几何模型按如下简化方式建立：

1）忽略发射过程中弹体外突结构对流场的影响；

2）只考虑喷管扩张段，喷管喉部给定入口条件；

3）认为导弹与发射箱之间无间隙；

4）忽略压力室入口处格栅、瓜瓣结构。

简化后，模型分为排气道、压力室、发射箱和导弹喷管喉部4个部分。计算模型如图1所示。

图1 燃气排导系统几何模型Fig.1 Geometric model of gas exhaust system

1.2 气相控制方程

导弹发射时，发动机喷管喷出的高速燃气流具有很大的马赫数，须将燃气流看作可压缩气体处理，在计算时，必须考虑喷管内流和外流之间的相互作用。针对这一复杂流场，本文应用可压缩的、雷诺N-S平均方程来对流场进行计算。N-S 方程是湍流方程的通解，对于这种复杂流场，可以通过求解如下湍流N-S方程组得出结果。

式（1）～（6）中：t 表示时间；ρ 是流体密度；u、v 和w是x、y、z 方向上的速度矢量的分量；Fx、Fy和Fz是微元体上x、y、z 方向上的合力；τx、τy和τz表示粘性应力τ 的在不同方向上的分量；p 为微元体的压力；k 为流体传热系数；cp为比热容；T 为气相温度；ST为粘性耗散项；R 是摩尔气体常数。

1.3 颗粒相控制方程

本文对燃气排导系统内颗粒相的数值模拟采用了确定轨道的颗粒轨道模型[9-16]。颗粒相在流场内经历了十分复杂的变化过程，为了简化计算，本文将颗粒相简化为性质不变且密度为均值的球形颗粒，并假设颗粒相的质量不发生损失。

基于以上假设，颗粒相控制方程如下。颗粒相连续性方程：

式（7）中：vpn是颗粒速度在流管截面的垂直分量；A是通道截面。

颗粒相的动量方程：

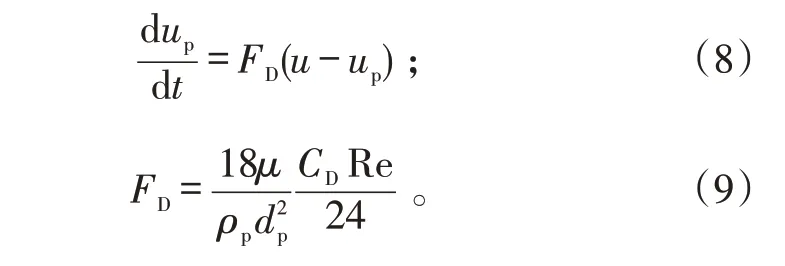
式（8）、（9）中：ρp为颗粒相密度；u 和up分别为气相以及颗粒相的速度；dp为颗粒直径；CD为颗粒相阻力分布。

雷诺数Re 定义为：

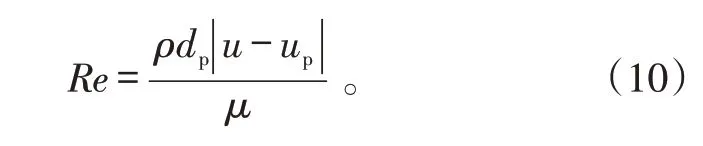
式（10）中：ρ 为气相密度；μ 为物理系数粘数。不同Re 下颗粒相阻力的分布为：

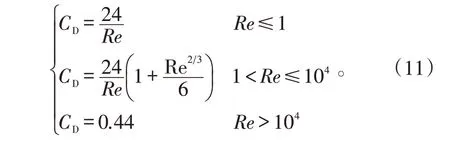
颗粒相的能量方程：

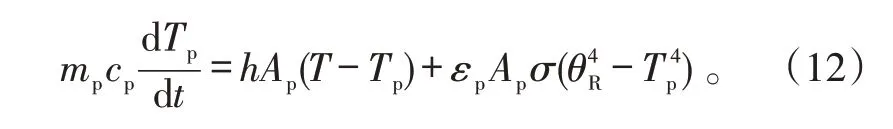
式（12）中：mp为颗粒质量；Ap为颗粒表面积；cp为颗粒比热容；T 为气相温度；Tp为颗粒相温度；h 为对流系数；θR为辐射温度。

1.4 湍流模型

本文研究的发射装置内燃气流属于高雷诺数流动，并且在压力室底部发生了很剧烈的弯曲运动，通过对3 种湍流模型[17]的优缺点进行分析，根据实际情况，选择标准k-ε 二方程模型对湍流流场进行计算：

1.5 两相耦合算法

对于颗粒轨道模型，一般采用“计算单元内颗粒源项算法”（PSIC）对两相流进行耦合计算。该方法首先对气相流场进行计算；然后，在流场环境中加入颗粒相并计算其运动过程中粒性参数的变化；将得到参数变化反馈到气相流场中，流场受到颗粒相的反馈作用发生参数的改变，这样交替对离散相与连续相进行求解，直到两相方程均收敛为止[18]。图2 给出了PSIC算法流程。

图2 PSIC算法Fig.2 PSIC algorithm

在进行两相耦合的计算过程中，颗粒相与气相的能量、质量以及热量都发生了交换，交换作用的方程式如下：

气固两相质量交换方程：

气固两相动量交换方程：

气固两相热量交换方程：

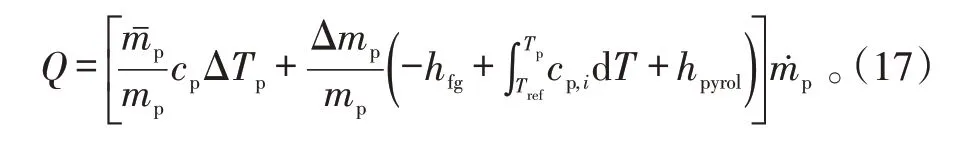
式（15）～（17）中：Δmp为颗粒相质量差；mˉp为平均颗粒相质量；F 为相间作用力；Q 为相间交互热；ṁp为颗粒质量变化率；hfg为对流系数；Tref为标准参考温度。

2 模拟计算

2.1 网格划分

本文对燃气排导系统整个计算区域采用六面体结构化网格进行离散。进行超音速流动计算时，对网格划分的要求很高，图3 为发射高度10dn（dn为喉部直径）时，对计算区域离散化所采用的网格。

后文中，不同发射高度下的模型均采用该方法对计算区域进行离散。

图3 部分计算网格Fig.3 Computing grid

2.2 燃气参数

含铝固体推进剂燃烧所产生的燃气流为高速、高温并且含有强烈腐蚀性的超音速流。燃气流内部成分十分复杂，很难对其进行完全的模拟，为了简化计算，进行如下假设：

a）认为燃气流是均质混合的气体；

b）燃气流与空气无化学反应；

c）燃气的比热比和热传导率恒定；

d）燃气流的分子粘性系数符合Sutherland定律。

燃气性能参数见表1。

表1 燃气性能参数Tab.1 Gas parameters

2.3 燃气颗粒相属性

2.3.1 Al2O3的物理特性

本文以球形Al2O3作为燃气中的固体颗粒，关注的对象主要是喷出喷管出口后的颗粒在流场中的运动。颗粒的物理参数按照喷管出口条件来计算更为合理。为了便于计算，假定在流动过程中颗粒相的比热、密度等参数为常值。

根据纯气相流场计算可得喷管出口平均温度为1 800K 。 Al2O3的温度由喷管出口温度来给定。Al2O3的熔点为2 318K，沸点为3 250K，在喷管出口处Al2O3呈固相，比热为1 254 kJ/(kg ⋅K)。根据Al2O3的密度随温度线性变化关系式[17]：

式（18）中：Tp为颗粒相温度；Tr为参考温度，对固相Al2O3取294.4 K ；ρmpr为参考温度下的颗粒密度，在294.4 K 时，Al2O3的密度为3 964.5 kg/m3。

计算得1 800 K 时，Al2O3的密度为3 800 kg/m3。

2.3.2 Al2O3的尺寸分布

颗粒尺寸分布是颗粒相最重要的特性。关于固体火箭喷管中的粒子分布，人们已经做了大量的研究。目前，学界基本认同Al2O3粒子在喷管出口处的尺寸分布服从对数正态分布：

式（19）中：σ 为正态分布的标准差；Dˉ为质量平均直径。

由文献[19]可知，本文入口条件下颗粒粒径集中在0.3～10 μm ，质量平均直径为4.23 μm ，约有96%的颗粒粒径小于15 μm。为了简化计算，选取5 组颗粒直径代表粒子尺寸正态分布对两相流场进行计算。图4为标准差σ=0.46，质量平均直径为4.23 μm的分布密度函数近似直方图。

2.3.3 颗粒相质量流量计算

应用FLUENT计算两相流时，须要在入口处输入各尺寸颗粒相的质量流率。喷管入口处颗粒相质量流率按照气相质量流率的20%加入。其中，喷管入口处气体质量流率计算式为：

2.企业在信息平台建设中的职责和权利。职业经理人信息平台建设主要是为企业的人才需求而服务，企业是最大的受益者，所以企业的职责主要包括提供职业经理人真实绩效技能信息、兑现职业经理人的劳动合同、查询企业拟选聘职业经理人信息等。

式中，

固体火箭燃气中，γ=1.216，R=270.3 J/kg，计算可得K=0.039 634。

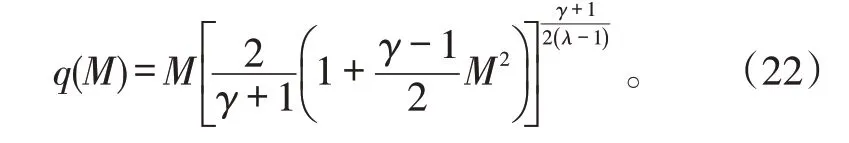
在喷管喉部M=1，则q(M)≈1。

本文中喷管喉部面积为4.753 89×10-3m2，计算可得ṁ=34.4 kg/s。每组颗粒的质量流率可以由燃气的质量流率与颗粒相的质量分数的乘积求得。

2.4 定解条件

2.4.1 颗粒相边界条件

入口条件：每组尺寸颗粒给定质量流率，假设喷管入口处颗粒相速度等于当地气相速度，在喷管入口处以面源的形式加入流场中，每组颗粒平均地由喷管喉部面进入流场。

出口条件：将排气道出口设为逃逸条件，颗粒溢出计算区域，颗粒轨道计算停止。

2.4.2 气相边界条件

入口条件：将喷管喉部设为流场的压力入口，给定总温总压，具体数值根据压比的实际情况来确定。

出口条件：将排气道出口设为流场的压力出口，排气道出口与外界相连，出口压力为一个标准大气压。

壁面条件：其余面均设置为无滑移固壁边界条件。

2.5 计算结果

本文从2个方面对燃气排导系统内的气固两相流场进行分析：

1）分析实际发射高度以及发射参数情况下的计算结果。重点讨论压力室内射流结构以及燃气排导系统内流动规律。

2）改变发射高度（喷管口距压力室底部的距离H）以及膨胀压比n（n=Pe/Pa，Pe为喷管喉部静压，Pa为外界大气压），分析以上因素对流场的影响。

2.5.1 实际发射工况下的三维流场分析

导弹在实际发射工况发射时，发射高度H=10dn，喷管喉部总压Po=10 MPa，气相温T=3 200.8 K。分别截取X=-0.943 m、Z=1.315 m、Z=0 m、X=0 m、Y=0.85 m、Y=0 m 这6 个截面以及压力室底面，讨论各截面流场参数分布情况。

1）X= -0.943 m 截面。图5 给出了X= -0.943 m截面各参数分布的情况。导弹点火后，燃气射流直射进压力室内。燃气流在喷管喉部的压力为10 MPa。燃气流压力在喷管内急剧下降，喷管出口处的压力为0.245 MPa。随后，燃气流离开喷管口，在压力室内迅速膨胀后被压缩，欠膨胀燃气射流在压力室内形成马赫结构，变为2 个波节。流场最大马赫数为4.2，出现在第1 个波节中心位置，随着燃气流向压力室底部流动，第2个波节中心马赫数降至3.3。在整个核心区域内，燃气射流都处于超音速状态。除射流核心区域外，燃气流在压力室内的壁面流动基本处于亚音速状态。燃气流贴附在压力室底部流动的过程中卷吸上部燃气形成漩涡结构。

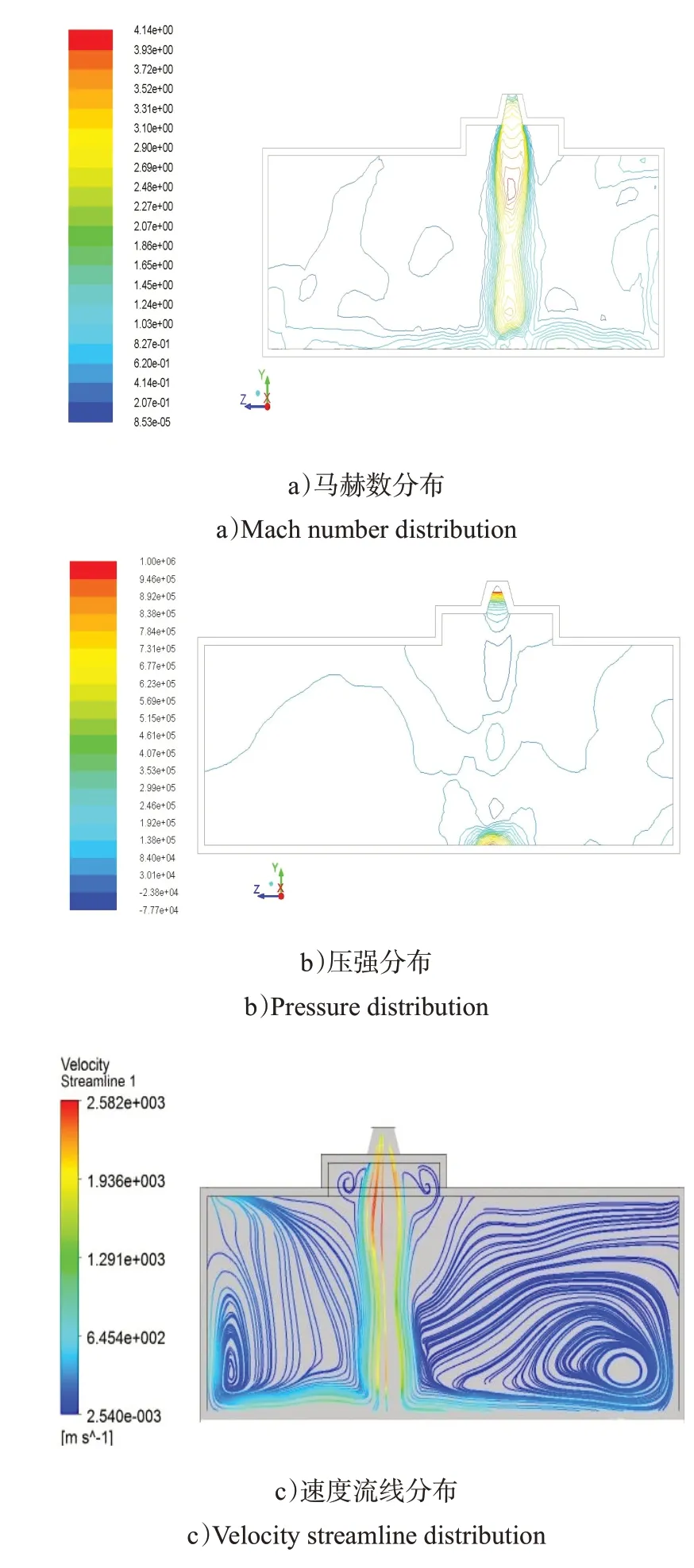
图5 X= -0.943 m 截面各参数分布Fig.5 Parameter distribution of X= -0.943 m

2）Z=1.315 m 截面。如图6 所示，压力室内压力值明显大于排气道内压力值，压力最大值出现在燃气流直射区域。由图6 可知，由于压力室底部导流板的作用，燃气流核心区域进入了排气道，而压力室侧壁附近燃气流由于没有足够的动能进入射流核心区域，在射流核心区域与压力室侧壁间产生了漩涡。激波后的超音速燃气流在贴附导流板流动过程中卷吸上部气流形成不同尺寸的漩涡结构。由于大量燃气流同时涌入排气道以及涡流动的挤压作用，有部分燃气流倒流回发射箱，由发射箱与弹体的间隙流出。自由射流区马赫数分布不规则，不存在相交激波，这是因为在两相射流中存在相间作用，颗粒不仅受燃气作用追随燃气运动，还受惯性作用保持原有运动状态影响气相速度的变化，使得气相在某个位置产生参数突变的可能性降低，从而阻碍了相交激波的形成。

图6 Z=1.315 m 截面各参数分布Fig.6 Parameter distribution of Z=1.315 m

3）Z=0 m 截面。Z=0 m 截面接近压力室侧壁。从图7 中可以看出，压力室侧壁区域燃气流主要为亚音速状态，燃气流通过导流板流向排气道，由于空间突然减小以及燃气的挤压作用，燃气流在压力室入口加速至超音速状态。压力室内部有着十分剧烈的漩涡运动，排气道入口处产生了较强的回流涡。

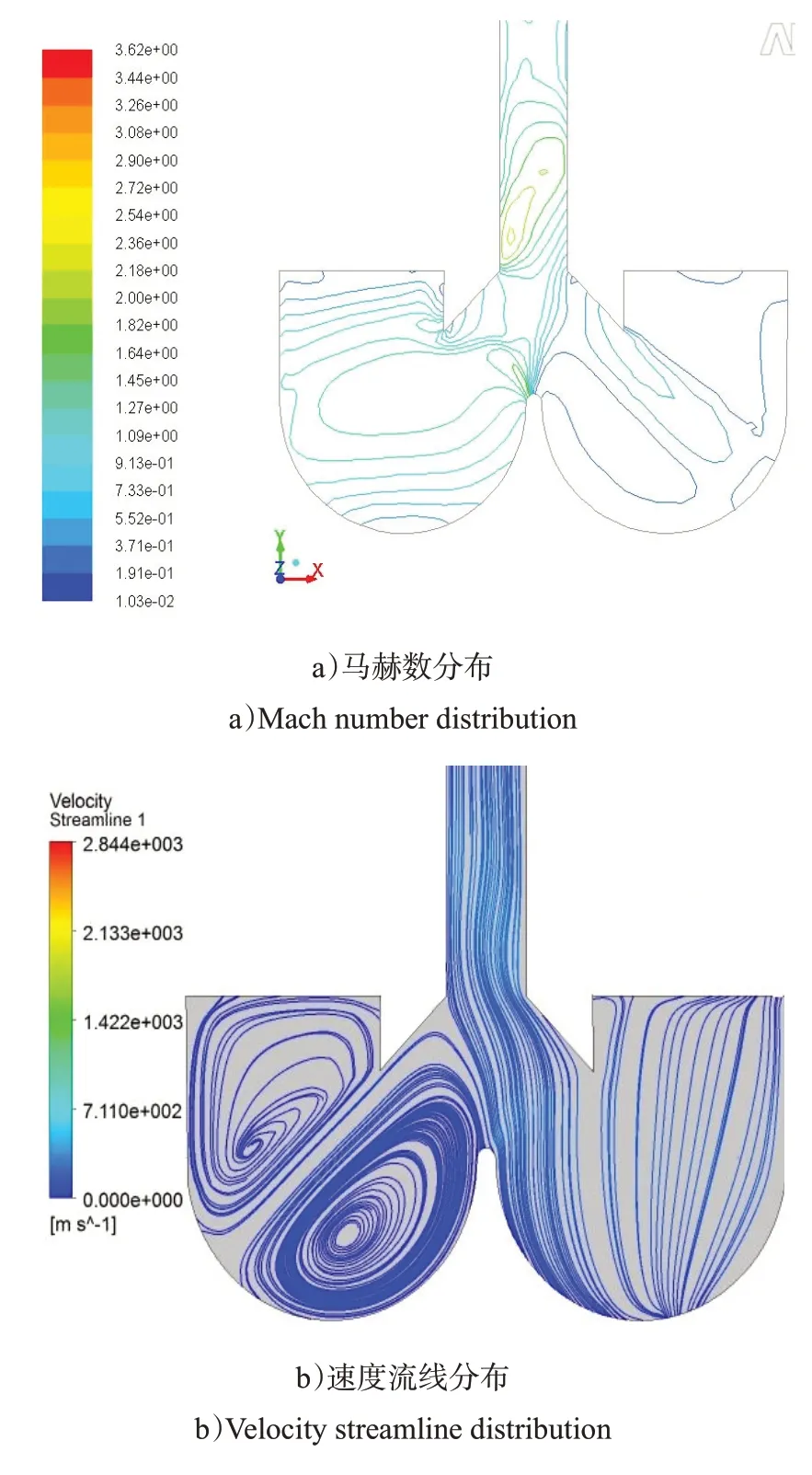
图7 Z=0 m 截面各参数分布Fig.7 Parameter distribution of Z=0 m

4）X=0 m 截面（排气道中心截面）。从图8 可以看出，排气道内燃气流马赫数与压力均沿Y 轴正方向逐渐减小，排气道内燃气流属于亚音速燃气射流。排气道内靠近直射发射位区域的马赫数与压力略大于其他区域。

图8 X=0 m 截面各参数分布Fig.8 Parameter distribution of X=0 m

5）Y=0.85 m 截面。Y=0.85 m 截面临近喷管出口位置，该位置燃气流在X 、Z 方向有很好的对称性。由图9可知，燃气流的核心区域为超音速燃气流，其他区域均为亚音速燃气流。

图9 Y=0.85 m 截面各参数分布Fig.9 Parameter distribution of Y=0.85 m

6）Y=0 m 截面。图10表示Y=0 m 截面燃气流马赫数等高线向Z 轴负方向偏移。流场变化的主要原因是压力室内存在漩涡结构，压力室壁面位置的漩涡流动如图10 b）所示。

图10 Y=0 m 截面各参数分布Fig.10 Parameter distribution of Y=0 m

7）压力室底部。由图11可知，由于超音速燃气流强烈的冲击作用，压力室底部燃气直射区域出现了一个强压区，该区域为平板激波结构。激波位置燃气流速降至亚音速，燃气流在压力室底部向四周流动的过程中膨胀加速至超音速，超音速燃气流受到压力室壁面的约束在壁面夹角处出现高压区。

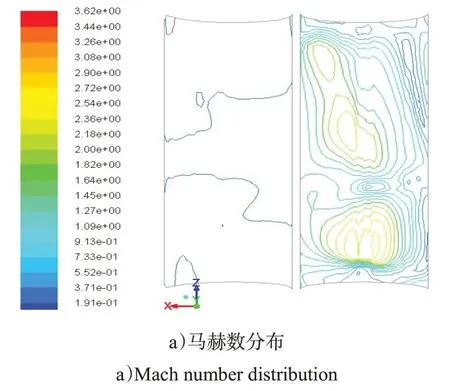
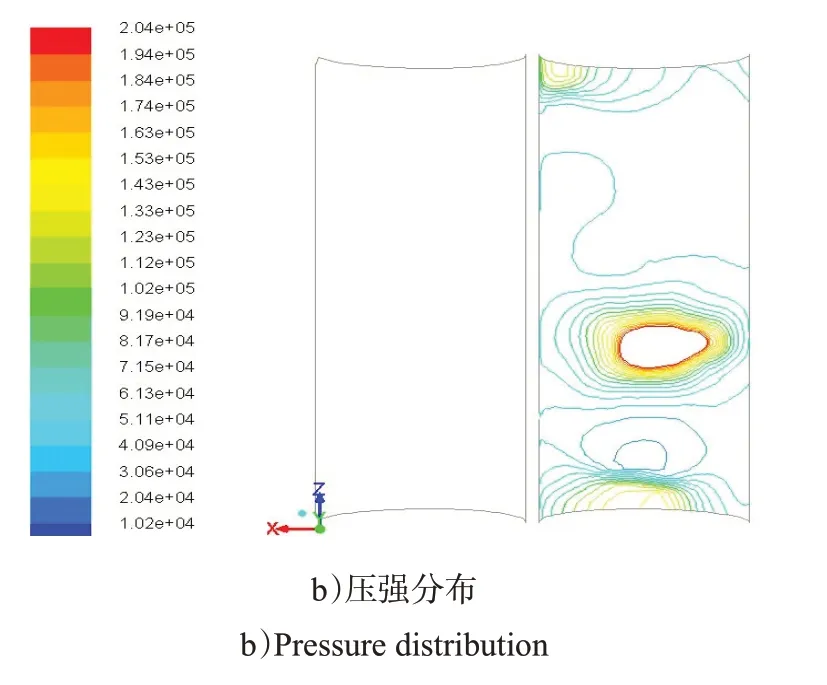
图11 压力室底部各参数分布Fig.11 Parameter distribution at the bottom of pressure chamber

通过对以上7组流场典型截面参数分布情况进行分析，燃气排导系统流场特征总结如下：

1）燃气流在整个核心区域内都处于超音速状态，在压力室以及排气道内基本处于亚音速状态；

2）射流核心区域由波节组成，各波节结构相似，波节随着射流流动方向逐渐减小。其中，心马赫数也逐渐降低；

3）压力室内部有着十分剧烈的漩涡运动，在压力室壁面夹角附近尤其明显，这些漩涡运动导致射流核心区域发生轻微偏移；

4）超音速燃气流冲击压力室底部形成激波结构，激波后燃气流贴附压力室底部向四周流动并膨胀加速至超音速，在壁面夹角处产生强压区；

5）排气道内燃气流马赫数与压力沿出口方向逐渐减小，并且压力略大于外界大气压。

2.5.2 流场影响因素分析

前文分析了实际发射高度以及发射参数情况下的流场参数分布。接下来讨论发射高度（喷管口距压力室底部的距离H）以及燃烧室压强Po对三维流场参数分布的影响。各情况计算参数如表2所示。

表2 计算参数表Tab.2 Calculation parameters

1）讨论发射高度对流场的影响。在给定入口压比情况下，分别对发射高度H 为10dn、15dn和30dn的3 种情况进行分析，讨论导弹发射高度对流场参数分布的影响。

从图12 中可以看出，当H=30dn时，燃气流核心区划分为4 个完整波节，波节随射流流动方向逐渐减小，最末端波节的中心马赫数降至1.35。随着发射高度减小至15dn时，燃气流核心区域分为3 个完整波节，第3 个波节中心马赫数降至3。当H=10dn时，燃气流核心区只划分出2 个完整的波节，但是燃气流末端波节中心的马赫数最高，为3.3。3种发射高度下的燃气流核心区域均为超音速燃气流。

图12 不同发射高度马赫数分布Fig.12 Mach number distribution at different launching heights

从图13中可以看出，欠膨胀燃气流的压力在发射箱内经过多个先上升后下降的过程形成激波结构。波节中心压力值随着燃气流动方向逐渐减小。随着发射高度的增加，燃气流末端波节中心压力值逐渐减小。

图13 不同发射高度压强分布Fig.13 Pressure distribution at different launching height

如图14 所示，当发射高度H=15dn时，燃气流冲击压力室底部形成激波，激波后燃气流贴附压力室底部向四周流动，燃气流膨胀加速至超音速。激波强度以及贴附压力室底部燃气流速度对比H=10dn时的有所降低。

图14 H=15dn 时压力室底部各参数分布Fig.14 Parameter distribution at the bottom of pressure chamber when H=15dn

由图15 可知，当发射高度H=30dn时，压力室底部激波现象与H=15dn时基本一致，但激波强度以及贴附压力室底部燃气流速度低于H=15dn时的状态。

图16 为不同发射高度下压力室底部X 方向压力曲线变化如曲线图。从图中可以看出，发射高度为10dn时，压力室底部产生的激波强度最大，压力室底部激波强度随着发射高度的增加而减小。

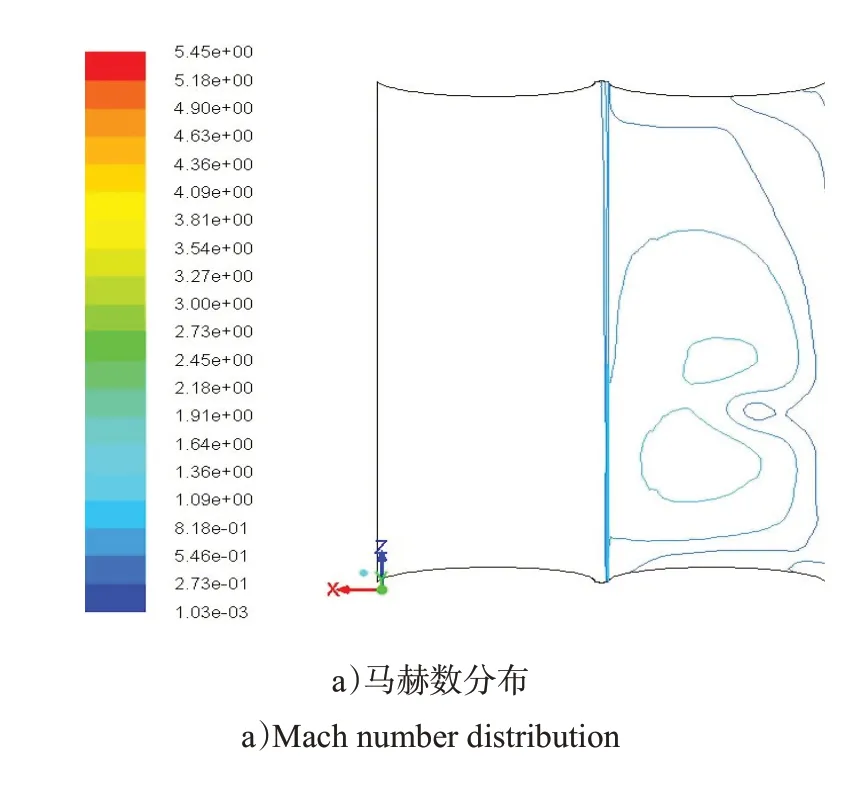
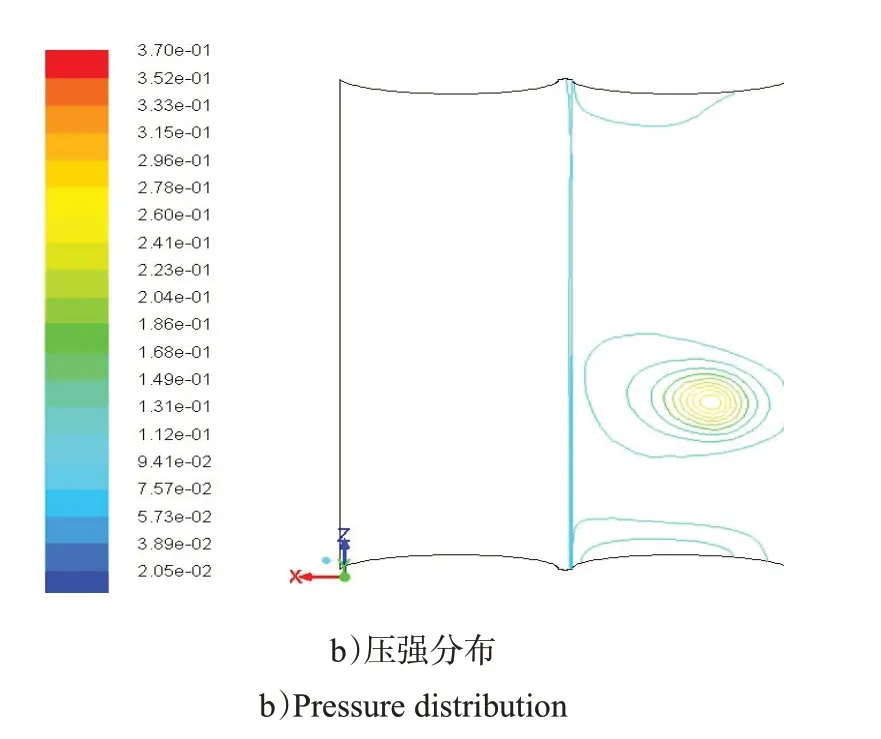
图15 H=30dn 时压力室底部各参数分布Fig.15 Parameter distribution at the bottom of pressure chamber when H=30dn

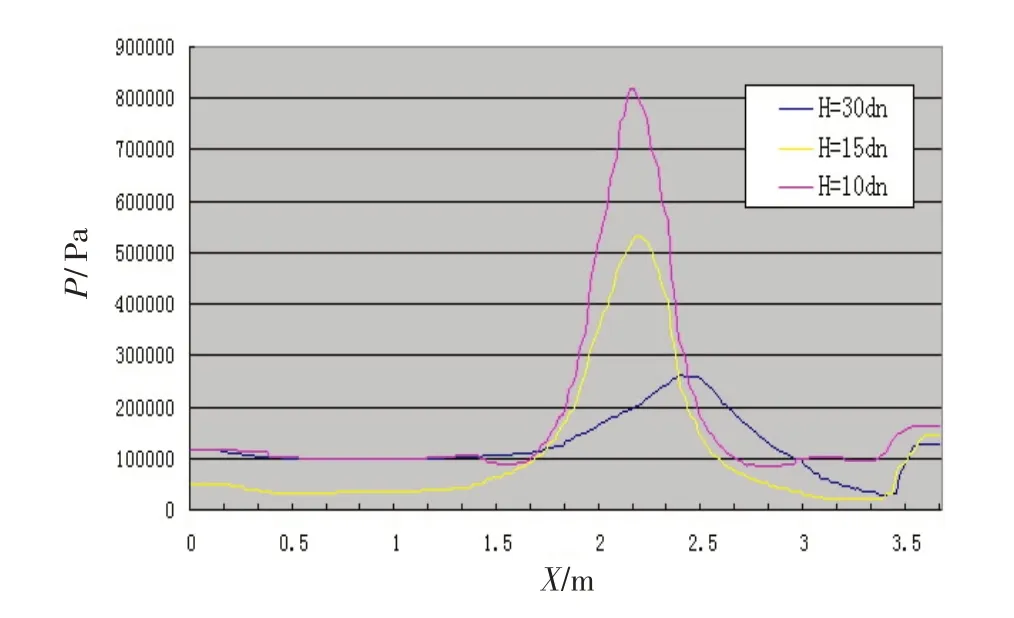
图16 不同发射高度下压力室底部X 方向压强分布Fig.16 Pressure distribution in the X direction at the bottom of pressure chamber at different launching height

综上分析，导弹发射高度对流场参数分布的影响主要表现在：随发射高度增加，燃气流冲击压力室底部产生的平板激波强度减小；燃气流核心区域波节数增加；燃气流末端波节中心马赫数以及压力值降低；贴附压力室底部导流板的燃气流速度降低。

2）讨论燃烧室压强对流场的影响。对于给定尺寸的喷管结构，膨胀压比n（n=Pe/Pa，Pe为喷管喉部静压，Pa为外界大气压）的改变就是燃烧室压强Po的改变。本文分别对压比为1.5、2.0和2.5这3种情况进行分析，讨论燃烧室压强Po对流场的影响。

图17为喷管轴心方向压强分布。由图可知，燃气压力在喷管内急剧下降；随后，压力在发射装置内经历了先上升后下降的过程，波峰出现在2个波节之间，压比n=2.5 时波峰压力最大并且波峰与喷管出口之间的距离最远，当燃烧室压强Po减小时，波峰与喷管出口之间距离以及波峰压力也随之变小。由于燃气流冲击压力室底部产生激波，燃气流在接近压力室底部时压力迅速上升。