110 kN 核热发动机推力室非平衡流动传热数值模拟研究
2020-10-31李子亮
李子亮,徐 凯
(北京航天动力研究所,北京100076)
1 引言
随着深空探测技术的不断发展,核热推进的优势逐渐显现,与化学推进相比,核热推进具有比冲更高、工作时间更长且不依赖太阳能的优点[1-2]。 核热推进的核心是核热火箭发动机,早在上世纪五十年代中期,国外就已开始核热火箭发动机的研制工作,具有代表性的是美国930 kN 推力的NERVA 发动机和苏联35 kN 推力的RD—0410 发动机[3-4]。 我国核热推进技术研究起步晚,基础较为薄弱,但反应堆工程技术基础比较雄厚[3]。 核热发动机发展的主要趋势是模块化和小型化,目前美俄重点发展30 ~100 kN、比冲900 s以上的核热火箭发动机,将多个核热火箭发动机捆绑使用,以满足不同任务需求[5-7]。
核热火箭发动机中的氢通过反应堆芯被加热至高温并经喷管膨胀做功产生推力,国外核热火箭发动机研制中普遍将核反应堆的设计作为重点,而对堆芯下游高温氢在推力室的流动传热过程关注较少[8]。 对于以氢为推进剂的核热火箭发动机,氢在流经推力室收缩扩张喷管时,气体的压力和温度不断变化,并伴随有限速率的离解反应,因此核热火箭发动机推力室流动传热的计算需要考虑氢气非平衡离解的影响。 非平衡流动广泛用于化学推进火箭发动机推力室流场的计算,目前核热发动机内氢的流动研究主要集中在低压高温非平衡流动二维计算和高温高压平衡流动的一维计算[9-10],而对推力室内高温高压氢非平衡流动对发动机性能参数的影响研究不充分。 鉴于此,本文以110 kN 核热火箭发动机推力室为研究对象,通过数值模拟方法对推力室的流动传热进行建模仿真,研究堆芯下游推力室内高温高压氢的非平衡离解作用对发动机性能和再生冷却传热的影响。
2 模型与计算方法
2.1 几何建模与网格划分
根据110 kN 核热火箭发动机设计参数建立推力室身部和喷管延长段三维几何模型,其中堆芯出口直径为416 mm,喷管面积比300,身部采用铣槽式再生冷却通道且数目可变,具体参数如表1 所示。
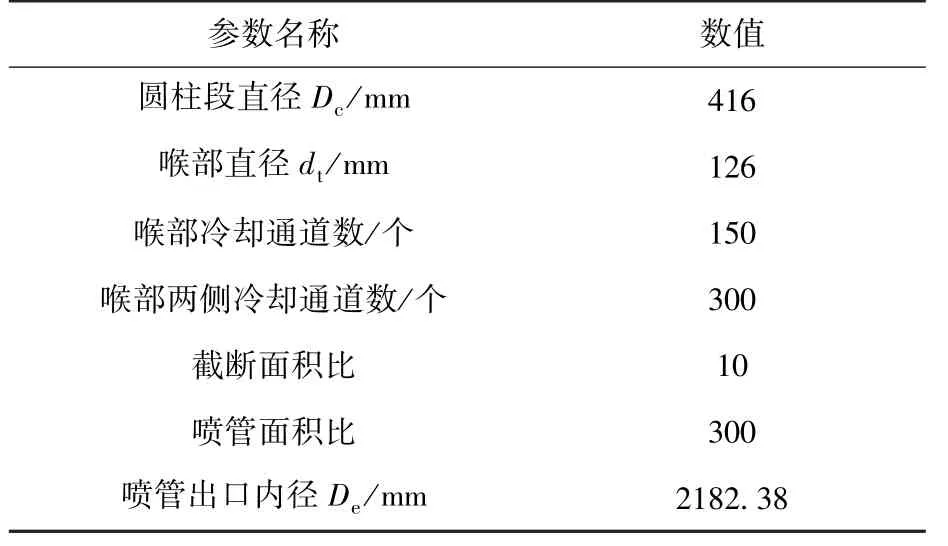
表1 推力室设计参数Table 1 Design parameters of thrust chamber
为节省计算成本,根据模型的周向对称性,选择夹角为1.2°的单个通道的推力室模型进行计算。 采用ICEM 软件对模型进行网格划分,计算域网格总数为654.974 万,其中以六面体网格为主,对与流体接触的壁面附近网格进行加密,保证壁面y+≈1,如图1 所示。
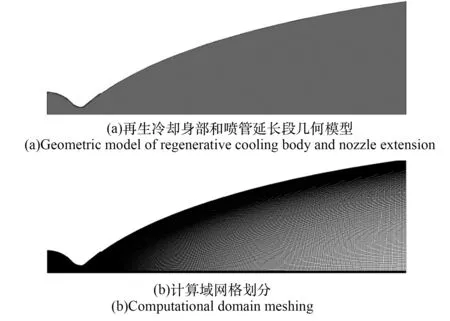
图1 推力室几何模型与网格划分Fig.1 Geometric model and meshing of thrust chamber
2.2 控制方程
气体在推力室的流动过程满足粘性N-S 方程,遵循质量守恒、动量守恒和能量守恒,气体控制方程如式(1)~(3)所示。
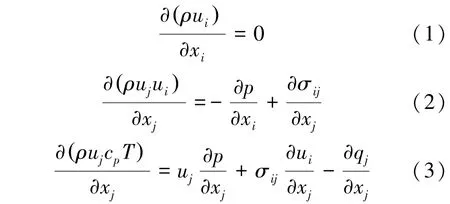
式中,μ 为分子粘度,qi为热流量,σij为粘性张量,cp为比热容,ρ 为密度,T 为温度,p 为压力。
固体传热控制方程如式(4)所示。
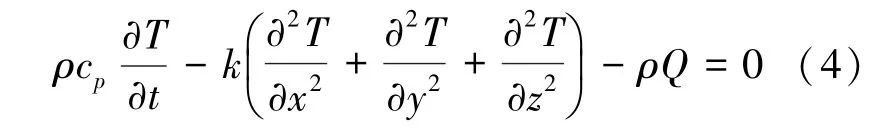
式中,Q 为热源,k 为导热系数。
2.3 湍流模型
SST k-ω 湍流模型是由k-ε 模型和k-ω 模型组成的复合模型,并充分集成了二者的优点。SST k-ω 湍流模型用湍流计算时,近壁面低雷诺数区采用k-ω 模型,远壁面完全湍流区采用k-ε模型,在计算受限空间流场时,SST k-ω 模型较其他双方程模型具有显著的优越性,因此,采用SST k-ω 模型对推力室流场进行计算。
SST k-ω 湍流模型的输运方程如式(5)~(9)所示。
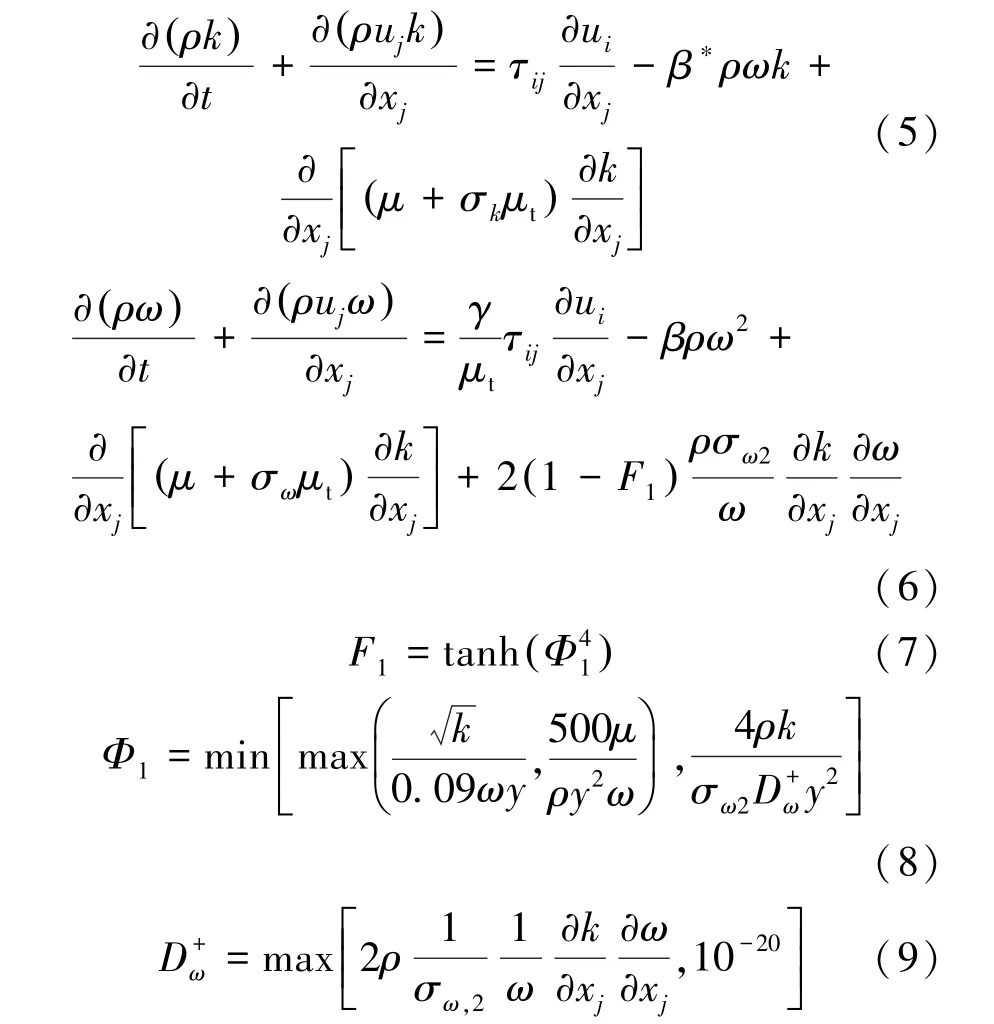
SST k-ω 模型湍流粘度表达式如式(10) ~(12)所示。
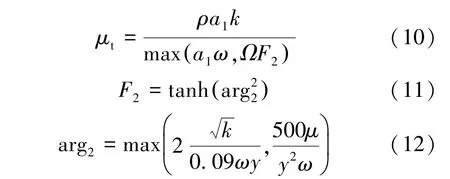
式中,τij为雷诺应力张量,Ω 为涡度张量,μ为层流粘度,μt为湍流粘度,y 为到壁面的距离,模型常数a1=0.31, β*=0.09, σk1=0.85, σω1=0.5, σk2=1.0, σω2=0.856。
2.4 化学反应模型
采用有限速率反应机理计算氢在推力室喷管内的非平衡流动。 氢离解的可逆反应式为式(13)。
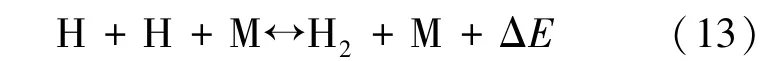
式中,M 代表H 或H2,ΔE 代表反应吸收或释放的能量。 氢的离解反应采用有限速率/涡耗散模型计算。
2.5 介质物性
经堆芯换热后的高温氢气满足理想气体状态方程,比热为温度的多项式函数,粘度满足苏萨兰公式,导热率满足动力学理论。 冷却通道内超临界氢的密度、比热、导热率和粘度随压力和温度变化,拟合为压力和温度的多项式,再生冷却传热内壁面与肋的材质为锆铜,外壁材质为电铸镍,将其比热、导热率拟合为温度的函数。
2.6 边界条件
将计算域边界设定为以下4 类边界条件:
1)入口边界条件:高温氢气的入口为压力入口边界,根据已知堆芯出口参数给定氢的入口压力、温度和组分含量;超临界氢的入口为质量流量入口,给定入口质量流量、压力和温度,并给定相应湍流的湍动强度和水力直径。
2)出口边界条件:氢气和超临界氢的出口均为压力出口,给定出口压力、温度和相应的湍动强度与水力直径。
3)壁面边界条件:内壁面为流固耦合壁面,给定粗糙度为4 μm,外壁面为非耦合壁面,定义其为光滑绝热壁面。
4)对称边界条件:计算域中过轴线的燃气、室壁和冷却通道两侧面为对称面。 无离解态是指氢分子不发生离解的状态;平衡离解冻结态是指在推力室入口氢气离解反应已达到平衡,喷管内的流动过程中气体组分不再发生变化;无热沉积非平衡离解态是指在不考虑热沉积的条件下氢气在喷管内非平衡流动的状态;热沉积下非平衡离解态是指考虑热沉积的条件下氢气在喷管内非平衡流动的状态。 在计算中通过定义入口初始组分和有限化学反应机理进行计算。 在计算热沉积条件下的非平衡流动时,将5 MPa 和2750 K 下离解平衡态的组分作为推力室入口的初始组分,假设反应堆中子在推力室的热沉积能量均匀分布,在计算中作为体热源。 推力室计算域主要参数如表2 所示。
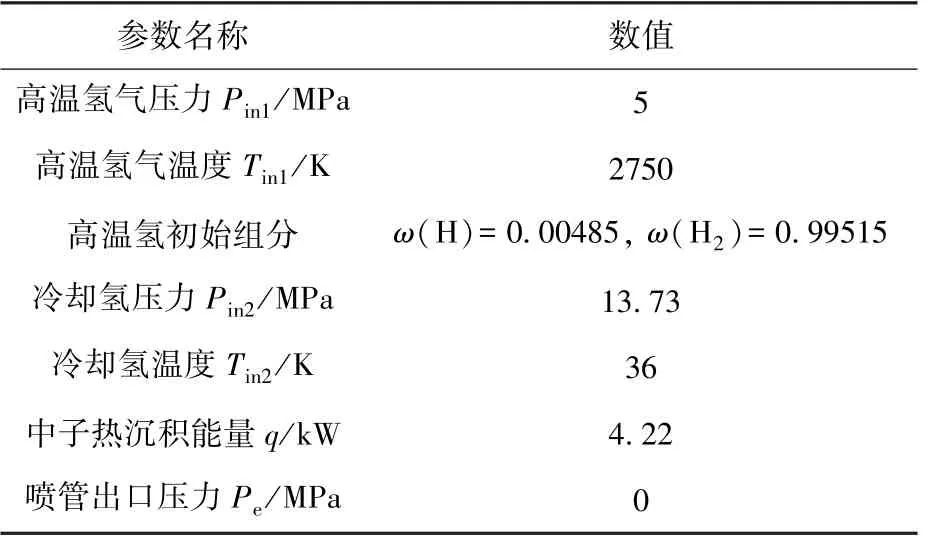
表2 计算域主要参数Table 2 Parameters of thrust chamber
2.7 计算求解
将流固界面作为耦合内壁面,对燃气和冷却剂的流动与壁面的传热进行同步耦合求解,采用DO 模型计算辐射传热过程;流体项采用二阶迎风格式进行离散,采用SIMPLE 算法处理压力和速度的关系,采用24 个CUP 进行并行计算求解,能量方程解的收敛精度为10-6,连续性和动量方程收敛精度为10-3。
3 结果与讨论
高温氢在推力室喷管发生非平衡离解反应时计算域主要参数分布如图2 所示。 可以看出推力室冷却通道内流体域的压力最大且温度最低;高温高压氢经喷管膨胀做功,轴向压力和温度不断降低,速度不断升高,并在出口达到最大值。
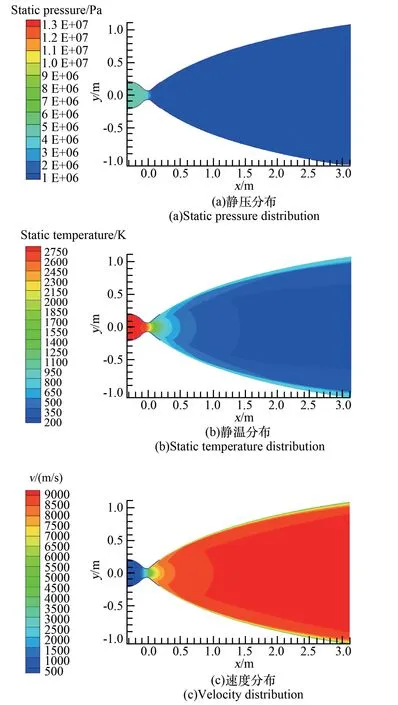
图2 非平衡离解态下推力室计算域内主要参数分布Fig.2 Main parameters distribution in the calculation domain of thrust chamber under non-equilibrium dissociation
图3 和图4 分别为非平衡离解态的氢分子和氢原子在推力室喷管内的质量分数分布。 高温高压氢在收缩扩张过程中,氢原子不断重组为氢分子,氢分子的质量分数逐渐增加,其中在喷管收敛段气体组分质量分数变化最大。 在相同的轴向位置,由于推力室身部再生冷却的作用,身部壁面附近气体温度较低,有利于氢原子的重组,从而使壁面附近的氢分子质量分数高于壁面远端流场中的质量分数,如图3 所示。
表3 为氢在无离解态、平衡离解冻结态、无热沉积非平衡离解态和热沉积下非平衡离解态的推力室再生冷却压降、温升和比冲计算结果,从表中可以看出,在4 种状态下,再生冷却氢的压降均为0.47 MPa,而温升和比冲存在差异。 非平衡离解态下的温升较平衡离解冻结态和无离解态稍高,这主要是因为喷管内非平衡态的氢随着轴向温度和压力的降低,壁面附近已离解的氢原子重新组成氢分子,并放出能量,对再生冷却传热起到促进作用。 无离解态和平衡离解冻结态下氢的温升接近,平衡离解冻结态的比冲要高于无离解态,这是因为平衡离解冻结态的氢中含有一定量的氢原子,气体密度更低,相同条件下其比冲更高;非平衡离解态的温升和比冲要高于平衡离解冻结态和无离解态,这是因为非平衡离解态的氢原子在喷管收缩扩张段重组为氢分子(图3 和图4),该过程放出的热量一部分使壁面传热增强,温升变大,另一部分热量转化为动能使喷管出口比冲增加。由于推力室上的中子热沉积能量很小,使得无热沉积非平衡离解态和热沉积下非平衡离解态的温升与比冲十分接近,因此,热沉积对喷管比冲和再生冷却传热的影响可以忽略。
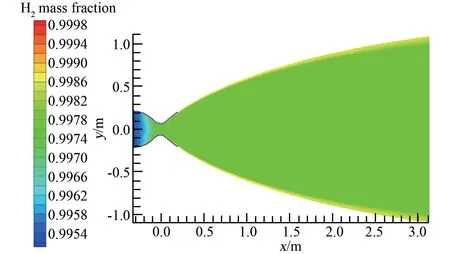
图3 非平衡离解态下的氢气质量分数分布Fig.3 Mass fraction distribution of hydrogen under non-equilibrium dissociation
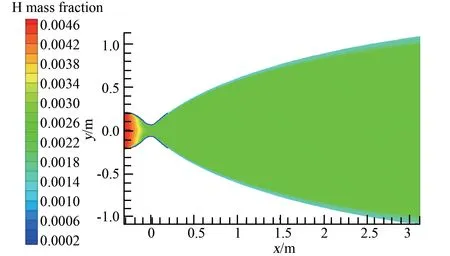
图4 非平衡离解态下的氢原子质量分数分布Fig.4 Mass fraction distribution of hydrogen atom under non-equilibrium dissociation

表3 不同状态下推力室主要技术指标数值计算结果Table 3 Calculation results of main technical indicators of thrust chamber under different conditions
图5 和图6 为不同离解态下推力室身部燃气壁面热流密度和温度的轴向分布曲线。 从图中可以看出,热流密度与壁面温度的峰值(57 MW/m2与522 K)出现在喉部(x =0)上游附近,且燃气壁面温度均低于材料的温度上限。氢为非平衡离解态时,喉部壁面热流与温度均高于无离解态与平衡离解冻结态,此外,当氢为无离解态和平衡离解冻结态时,壁面热流密度与温度十分接近。
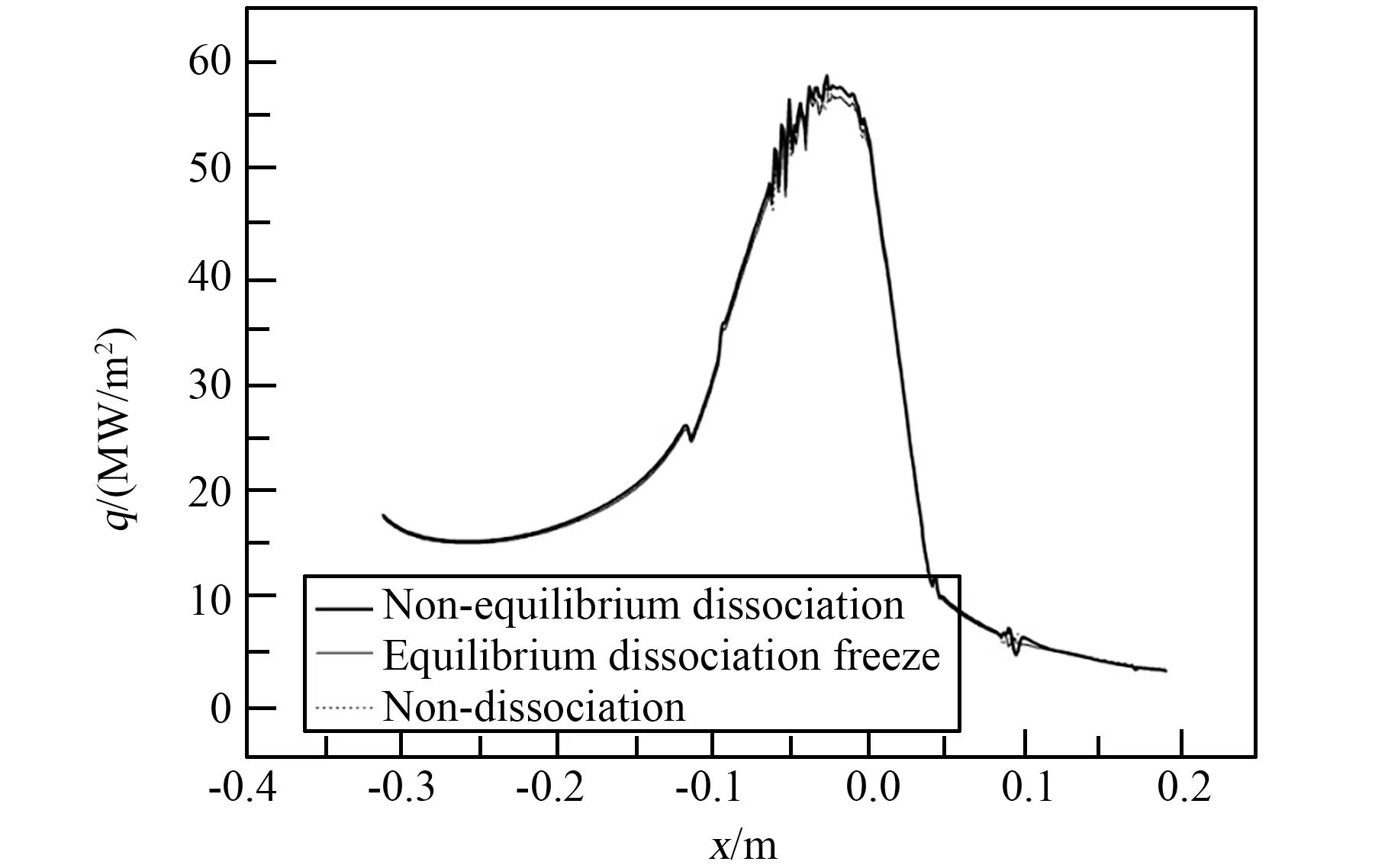
图5 不同离解态下燃气壁面热流密度轴向分布曲线Fig.5 Axial distribution curve of heat flow density on thrust gas wall under different dissociation state

图6 不同离解态下推力室燃气壁面温度轴向分布曲线Fig.6 Axial distribution curve of temperature on thrust gas wall under different dissociation state
4 结论
1)110 kN 核热发动机推力室流动传热仿真中应考虑非平衡有限速率离解反应对再生冷却传热和发动机比冲的影响,该计算方法更加合理。
2)高温离解的氢原子在喷管内会发生重组并放出热量,非平衡离解态下计算得到的温升、比冲、喉部壁面热流密度与温度均高于无离解态和平衡离解冻结态的相应值。
3)反应堆中子在推力室热沉积对再生冷却传热影响很小,在计算中可忽略不计。
