基于大数据驱动的地方经济短期预测研究

吴睿辉，周湘贞

（1.广州南洋理工职业学院，广东 广州 510900；2.中国社会科学院 财经战略研究院，北京 100028）

随着大数据技术的不断发展，将大数据技术的强大分析能力运用于地方经济统计与分析成为可能。经济指标组成复杂且统计难度大，仅仅依靠每年政府公开的基本统计数据来进行分析效率低下［1］，因为政府的数据统计具有一定的滞后性，再者政府的统计数据有相当一部分是依靠人工统计及汇报统计，数据的完整性和精确性较差。经济发展易受社会环境的变化，或者不确定因素的影响，仅仅靠人工统计数据也无法分析微观环境对地方经济带来的瞬态影响。因此，基于大数据驱动和大数据技术的地方经济分析为地方经济预测及分析带来新的机遇。地方经济短期预测的意义在于为决策者提供近期政策规划的科学支撑。

大数据驱动为地方经济预测分析提供了数据支持［2］，还需要有数据分析工具或者方法对大数据进行细致分析。当前，采用机器学习或者深度学习算法在经济预测方面已经取得了一些成就，文献［3］和文献［4］均采用神经网络算法对地方经济实现预测，前者是基于最小绝对收缩和选择算法（Least absolute shrinkage and selection operator，Lasso）优化算法，后者结合小波理论进行优化，均取得较好效果。但是，上述方法在实际应用中的准确度不够理想。短期经济预测的关键内容是GDP预测，其直接影响了整体经济发展趋势，也是经济预测的关键指标。本文基于大数据环境，采用深度信念网络（Deep belief network，DBN）算法来完成地方经济短期GDP预测，以进一步提高地方经济预测的准确度。

1 地方经济指标获取

选取GDP作为经济预测对象，以便最直接地反映经济发展状况。为了建立地方经济短期预测模型，必须对影响地方经济的类别及相关指标进行提取，全面评估影响地方经济的各要素，尽量提取与地方经济相关度高的指标。

本文选取了5个类别共15项预测指标［5-6］，如表1所示。经济环境类、进出口类和消费类指标可以通过政府网站的公告数据、年鉴等渠道获取。投资和资源类指标利用爬虫程序通过互联网动态获取最新数据［7］。在Python等平台上利用Numpy工具包将指标自动地进行表格输出，同时调用开源的Tushare财经数据API进行数据采集。

选取地方经济预测对照样本后，进行地方经济短期预测指标选取，将所有预测指标归一化处理，再结合地方GDP生产总值生成带标签的特征向量，最后通过算法学习得到预测结果。

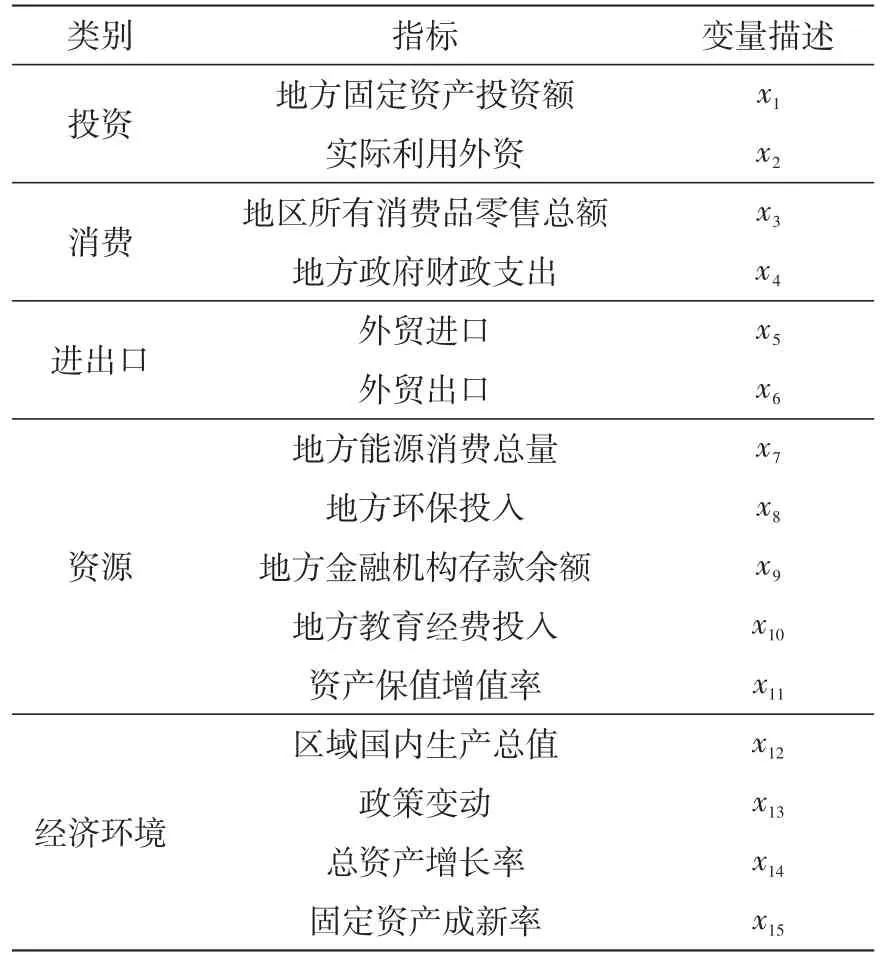
表1 经济预测指标Tab.1 Economic forecast index

2 DBN算法分析

设DBN的可视层为v=(v1,v2,…,vm)，隐藏层为h=(h1,h2,…,hn)，(v,h)∈{0,1}m+n，一个稳定的受限玻尔兹曼机（Restricted boltzmann machine，RBM）由能量参数θ={w,c,b}决定，w为两层间的权值，c和b分别表示各自的偏移。

可视层相对于单个隐藏神经元的概率为［8］

式中：P(v,h)求解只考虑了1个神经元，那么对n个隐藏神经元作用于可视层的概率为

可视层m个神经元作用于隐藏层概率［10］

针对m个可视神经元，第i个隐藏神经元被触发概率［10］

针对n个隐藏神经元，第j个可视单元被触发的概率为［11］

其中，机概率函数σ(·)为

对于N个输入样本v=(v0,v1,…,vN)，且v0,v1,…,vN独立同分布，因此

样本集v的似然估计记作

要求解L(θ)的最大值，可以转化为求解lnL(θ)最大值［12］

式中：η为学习速率，且η＞0。

对于单个样本v0=(v01,v02,…,v0m)，对样本进行对数求解［13］，得

式（12）对θ={w,c,b}求偏导得

条件概率满足

将式（14）代入式（13）得

对θ={w,c,b}的3个参数w、c、b分别求偏导，得到

现在得到RBM的3个参数的更新方法［14］

这种更新方法称为RBM的预训练，满足迭代次数阈值时，输出得到稳定的RBM结构。

对于包含l层隐藏层的DBN，h=(h1,h2,…,hl)，那么可视层的联合概率分布为［15］

DBN网络由多层RBM叠加而成，其中k=0,1,2,…,l-1，h0=u。

通过预训练得到θ={w,c,b}初始优化值，然后采用反向传播算法，继续微调θ={w,c,b}，当预测误差达到规定阈值时，算法结束，得到稳定的DBN模型。

3 实例仿真

为了验证大数据环境下DBN深度学习算法对地方经济短期预测的性能，采用Matlab进行实例仿真。以重庆市为例，结合年鉴获得2009至2018年共计10年的部分经济数据，剩余指标数据通过爬虫程序获得，将两者获得数据进行Python处理，进行归一化和向量化处理生成数据样本，样本按年度共分为10组。

3.1 DBN网络规模对经济短期预测的性能影响

参照表1，选取15个经济指标作为数据样本，地方GDP值作为预测对象，通过DBN深度学习算法来预测2018年度之后的GDP值。将2009至2016年共7组的经济数据样本作为输入，分别对2017、2018和2019年度的GDP值进行预测，与实际3个年度GDP值19 500.27亿元、20 363.19亿元和23 605.77亿元进行对比，设置预测准确率阈值为90%。

3.1.1 隐藏层层数对经济预测的影响 隐藏层层数对均方误差（Mean square error，MSE）和训练时间的影响如图1所示。随着隐藏层数Lh增加，经济预测的MSE在减少，Lh数从1至2，MSE从0.3以上迅速下降至0.1以下，下降幅度大；Lh在［2，6］区间，MSE缓慢下降，当 Lh超过4时，MSE趋于稳定；在DBN规模为1和2时，虽然MSE较大，但对经济预测的适应度较差，因此过小的DBN规模并不适合用于地方经济短期预测。

随着Lh增大，训练时间增加，特别是当Lh在4以上时，训练时间快速增加；当Lh为6时，训练时间达到了1 300 s；而 Lh在［1，4］区间，训练时间变化较小。原因是Lh增加使预训练时间增加，但反向微调权重的时间却在减少，两者综合使训练时间变化较小。

综合而言，隐藏层数为4时，MSE接近稳定，且训练时间未有明显增加，在MSE和预测时间之间折中平衡，将Lh设定为4时，能够较好地满足地方经济预测的需求。

3.1.2 隐藏层神经元数量对DBN预测性能的影响 对隐藏层神经元数量Nh进行差异化设置，同样设置预测准确度阈值为90%，验证MSE对Nh的敏感度。初始设置每层Nh分别为［2，3，4，5］，共计4层，总量为［8，12，16，20］，利用剩余的3组样本对模型进行测试，对比中国统计年鉴重庆市获得的实际值，求解不同规模结构下的均方误差。结果见表2所示。

当Nh变化时，3组样本的均方误差变化较小。均方误差并不总是随着隐藏层神经元数据量的增加而减小，当Nh为16时，3组样本预测的均方误差最小，当神经元数量为20时，预测误差增加。因此设置Nh等于16，更适合重庆市经济预测。

3.2 不同算法对地方经济短期预测的性能分析

为了进一步验证本文算法在地方经济短期预测的性能，采用本文算法与其他常用的4种经济预测算法，对比分析2017、2018和2019年度经济GDP总量。DBN网络Nh为16个，Lh为4层。仿真计算3个年份预测平均准确率和平均MSE，结果如表3所示。

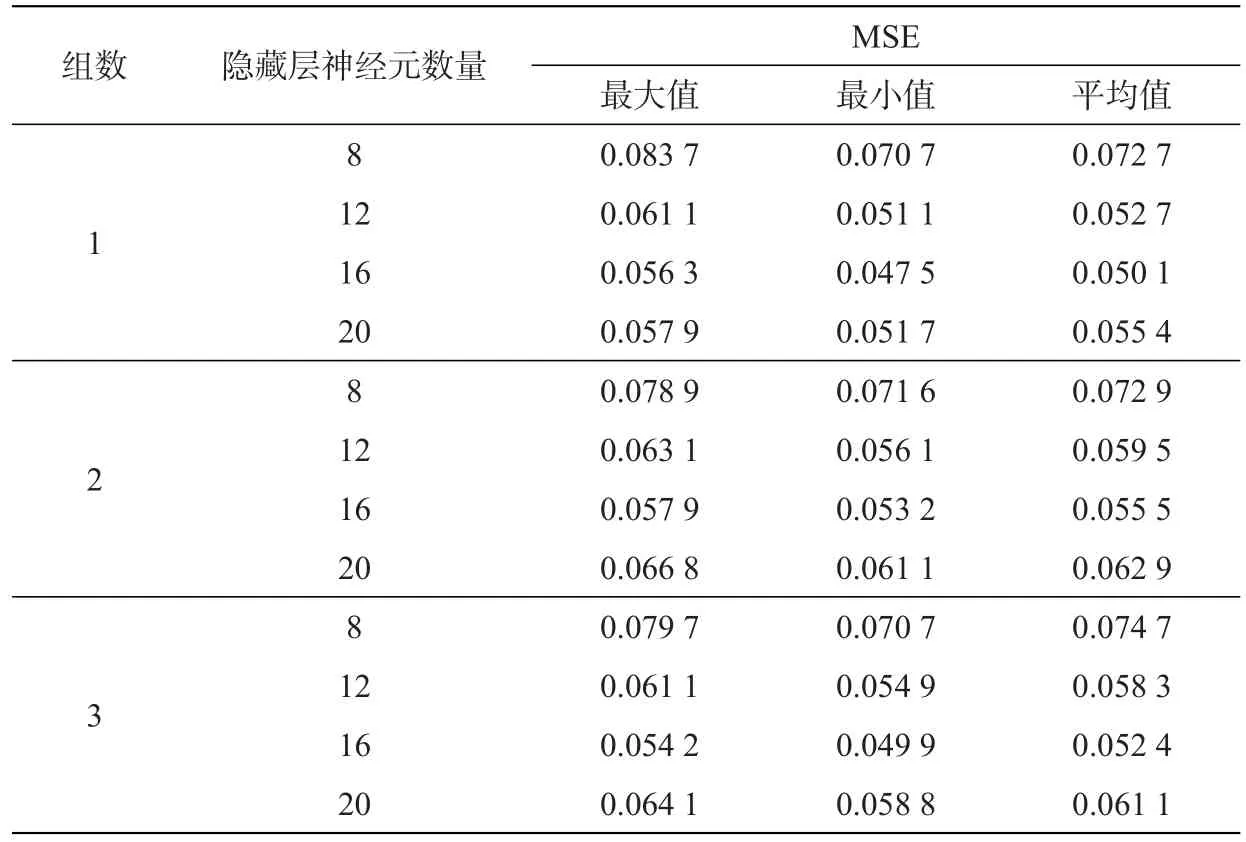
表2 不同网络规模的预测均方误差Tab.2 Prediction mean square error of different network scales

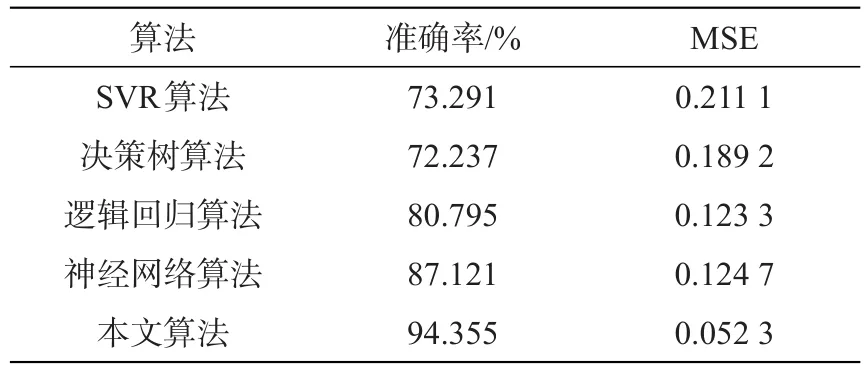
表3 不同算法的经济预测准确率和MSETab.3 Economic prediction accuracy and MSE of different algorithms

本文算法在地方经济短期预测准确率优势明显，达到了94.355%，SVR和决策树算法的预测准确率较差，神经网络和逻辑回归算法的准确率虽然达到80%以上，但是这2种算法的MSE均超过了0.1，表明这2种算法对地方经济短期预测的性能并不稳定，本文算法的MSE为0.0523，性能最优。

4 结 论

在大数据环境下，方便获取地方经济数据样本，结合DBN深度学习算法来实现对地方经济短期预测。以地方GDP为预测对象，通过DBN深度学习算法完成地方经济短期预测。在DBN训练过程中，进行权重参数的正反向交叉调节，获得最优参数后确定DBN结构。实验结果表明，相比于常用经济预测算法，基于DBN深度学习算法对地方GDP的预测准确度更高，且MSE较小。后续研究将进一步从DBN网络规模、学习率等方面研究，以提高地方经济短期预测的时间性能。也可将年度预测改为季度或者按月预测，进一步细化地方经济短期预测粒度，提高大数据驱动下的地方经济短期预测的适用度。