基于ANSYS的双连拱隧道开挖有限元分析

束永峰 杨毅

摘 要：本文使用ANSYS这一有限元分析软件对公路双连拱隧道开挖的过程进行有效的数值模拟，通过对建立的模型进行4次载荷步模拟，从载荷步的模拟可以得出一系列云图，这些云图可以理论上精确反映出公路双连拱隧道的围岩及支护结构的应力应变及内力的动态变化.通过对应力应变及内力的变化规律的分析，了解开挖过程采用的支护结构以及开挖方式的安全性及可靠性.从而让施工单位分辨清围岩及支护结构的复杂变化规律，提高施工过程的安全性.

关键词：有限元分析;载荷步;应力应变;安全性;可靠性

中图分类号：U452  文献标识码：A  文章编号：1673-260X（2020）08-0043-05

引言

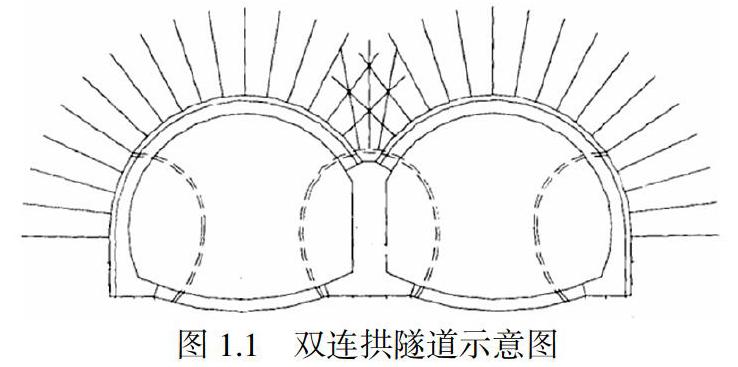
近些年来公路双连拱隧道在大跨度隧道工程中的使用越来越频繁，双连拱隧道有诸多优点，例如其占地面积较小，从而使得空间的利用率大大提升;其次双连拱隧道的开挖有利于连续作业，使得工期得以缩短，造价有所降低.正由于双连拱隧道的使用的频率之高以及它具有的这些优点，因此本文拟采用ANSYS有限元分析软件对一双连拱隧道开挖进行数值模拟.

1 工程概况

该公路双连拱隧道位于合肥某公路隧道，隧道处于V级围岩，跨度为23m，单拱为单心圆，墙的厚度为1.6m.采用？覫25锚杆作为支护结构，每边的隧道洞各使用20根？覫25锚杆.混凝土采用C30的混凝土.根据本工程的施工法案可以明确此公路双连拱隧道采用中导正洞全断面法开挖的方法.

2 模型建立

2.1 基本假定

为了简化运算，做出如下几条基本假定

（1）土体为理想的弹塑性材料.

（2）同一材料均质、各项同性.

（3）锚杆为弹性体.

（4）不考虑支护结构施工对土体的扰动.

2.2 本构模型

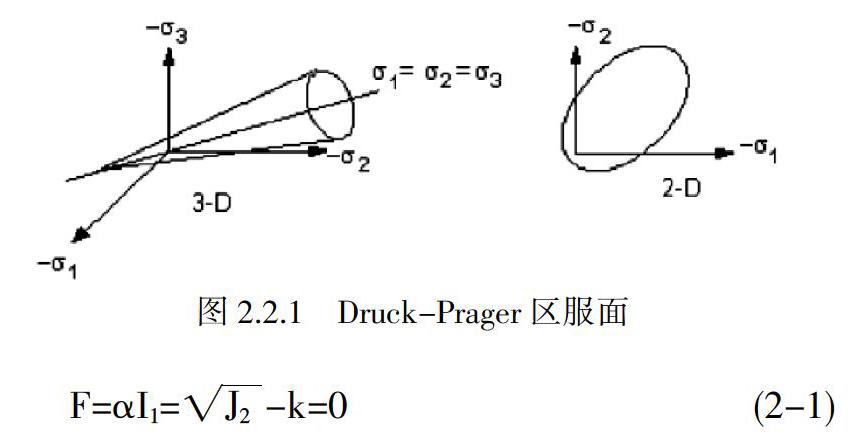
混凝土、土体以及岩石这些材料的受拉区的区服强度远小于受压区的区服强度，并且在材料受到剪力的时候，颗粒会因此而膨胀，所以在这种情况下，这些材料不适合Vonmise区服准则，相应的采取土力学中一个十分准确且经典的Druck-Prager区服准则.在土力学上将这些符合Druck-Prager区服准则的材料称之为DP材料，这给本次ANSYS建模提供了理论依据，因此这次建立的ANSYS模型，用DP材料来模拟混凝土、土体以及岩石，运用Druck-Prager这一十分准确且经典的区服准则会使分析到的结果更加准确.Druck-Prager区服面如图2.2.1所示.

2.3 模拟时采用的材料的各项力学参数

围岩的参数以及材料的参数分别如表2.2.1和表2.2.2所示.

2.4 计算模型的建立

模型的建立对于隧道的数值分析至关重要，选择什么样的模型很大程度上决定了计算结果的准确性，因此在此双连拱隧道选择的模型应该合理的反应实际情况，并且可以反应其边界条件以及外部荷载.隧道工程的几何形状以及围岩的初始应力十分复杂，因此要忽略掉一些无关重要的因素，退而求其次的选择重要的因素，这里采用岩土力学的数值计算计算方法——围岩和支护结构视为一整体，共同作为隧道的受力体系.因此此双连拱隧道的计算模型采用——复合整体模型，这样就简化了网格的划分以及节约了计算时间.在建模的时候针对后期不同步骤的岩土赋予不同的材料编号，除此之外要善于利用单元分组的功能，这样可以使后期复杂的操作步骤变得明了.

另外在此次的ANSYS建立模型时，参照王新敏教授《ANSYS机构分析单元与运用》这本教材.用具有塑性、蠕变、辐射膨胀等特性的平面单元PLANE42模拟围岩;用具有拉、压、弯性能的特征的梁单元BEAM3模拟衬砌结构;用具有承受单轴拉压特性的杆LINK1单元模拟锚杆.

邊界条件.隧道开挖的实际上边界条件在无穷远处位移为零的位置，然而在ANSYS模拟过程中，这一个边界条件是取不出来的，需要对建模的边界条件进行简化，使其建立的模型在分析的时候依旧有意义，故在一定特定范围进行模拟.本文建立的ANSYS模型的边界条件为x方向取离隧道中心距离为左右60m，下边界取离隧道中心距离为40m.

几何模型和网格划分如图2.4.1所示.边界条件如图2.4.2所示.

2.5 连续施工的计算

连续施工的的计算通过开挖过程中ANSYS软件所得到的云图对应的数据.在实际的建模过程中，用载荷步和杀死单元的办法来模拟隧道开挖过程.

通过采用王新敏教授《ANSYS工程结构数值分析》教材中介绍的杀死单元的方法来选取需要的节点编号，通过节点编号的选取来模拟挖去的围岩编号，杀死单元的方法简明扼要.根据施工方案，此双连拱隧道主要使用锚杆进行支护，锚杆嵌入岩体中，可以和岩体形成一个的稳定的整体结构，在实际的模拟也是将锚杆和岩体当做一整体，这一可以极大地提高岩体的的整体性和安全性;另外锚杆对隧道表面岩体的受力状态得以发生变化，让原本岩体表面的二项受力状态变为如今三项受力状态.

根据隧道开挖有限元分析中，载荷步常用的方法是将载荷步分为4个步骤进行，此论文沿用此方法.载荷步1：计算自重应力场;载荷步2：首先进行中导洞开挖，然后对中导洞进行支护，最后浇筑中墙部分;载荷步3：首先进行回填中墙的左侧部分，然后开挖右洞部分，支护右洞部分，最后对仰拱进行浇筑;载荷步4：首先开挖左洞部分，然后对左洞进行支护，最后浇筑仰拱.

由上述的四步载荷在ANSYS软件中可以得到四个双连拱隧道模拟求解迭代收敛过程图（横轴代表累计迭代数，纵轴代表绝对收敛准则），载荷步1、载荷步2、载荷步3、载荷步4的求解迭代收敛过程图分别如图2.5.1、2.5.2、2.5.3和2.5.4所示.

3 计算结果分析

3.1 载荷步1对应的云图

载荷步1：计算自动应力场.总位移矢量云图、等效应力云图分别如图3.1.1和图3.1.2所示，由图3.1.1可以得出在载荷步1时的总位移矢量的最大值为0.009115m.由图3.1.2可以得出在载荷步1时的等效应力的最大（小）值分别为707182Pa和12353.1Pa.

3.2 载荷步2对应的云图

载荷步2：中墙等效应力云图、初期支护弯矩云图、初期支护轴力云图及总位移矢量云图分别如图3.2.1、3.2.2、3.2.3和3.2.4所示.由图3.2.1可以看出中墙等效应力的最大（小）值分别为0.375×107Pa和309174Pa.由图3.2.2可以得出初期支护弯矩的最大（小）值分别为27196.6N/m和-27173.2N/m.由图3.2.3可以得到初期支护轴力的最大（小）值为36045.1Pa和-249355Pa.由图3.2.4可以得出总位移矢量的最大值为0.344×10-3m.

3.3 载荷步3对应的云图

载荷步3：初期支护和右隧道衬砌弯矩云图、初期支护和右隧道衬砌轴力云图、隧道锚杆轴力云图和总位移矢量云图分别如图3.3.1、3.3.2、3.3.3和3.3.4所示，由图3.3.1可以得出初期支护和右隧道衬砌弯矩的最大（小）值为118732N/m和-118782N/m.由图23.3.2可以得出初期支护和右隧道衬砌轴力的的最大（小）值为83427.8Pa和-993342Pa.由图3.3.3可以得出隧道锚杆轴力的最大（小）值为7068.14Pa和552.657Pa.由图3.3.4可以得出总位移矢量的最大值为0.001328m.

3.4 载荷4对应的云图

载荷步4：隧道衬砌弯矩云图、隧道衬砌轴力云图、隧道锚杆轴力云图和总位移矢量云图分别如图3.4.1、3.4.2、3.4.3和3.4.4所示.由图3.4.1可以得出隧道衬砌弯矩的最大（小）值为133393N/m和133331N/m.由图3.4.2可以得出隧道衬砌轴力的最大（小）值为-292325Pa和0.12×107Pa.由图3.4.3可以得出隧道锚杆的最大（小）轴力分别为8050.34Pa和-3838.5Pa.由图3.4.4可以得出总位移矢量的最大值为0.001328m.

4 计算结果分析

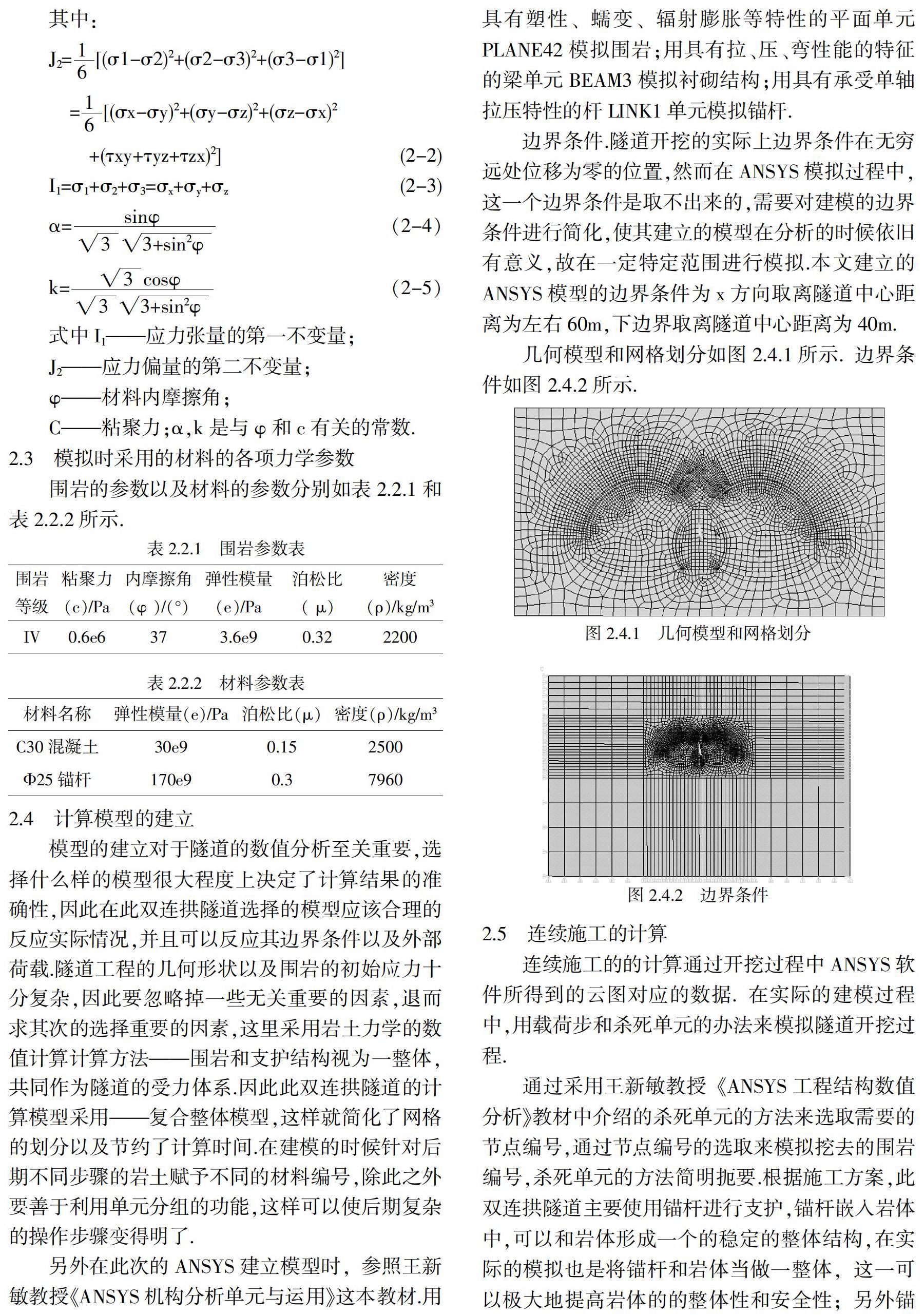
锚杆的极限锚固力：

P=K·Nt=D·L·qr  （4-1）

式中K——安全系数

Nt——锚杆轴向拉力设计值

D——锚固体直径

L——锚杆锚固段长度

qr——灌浆体与地层间的粘结强度设计值，可取0.8倍标准值

查找《基坑工程手册》可以得到锚杆灌浆体与一般岩体（软岩）间的粘结强度标准值为0.3～1.0MPa，在这里取最小值qr=0.3Mpa，在施工方案里锚杆入岩土的深度为L=2m，D=25mm，由上式可以得P=K·Nt=？仔·D·L·qr=3.14×25×10-3×2×0.8×0.3×106=37680Pa.在上述的ANSYS1模擬过程中锚杆的轴力都没有超过锚杆的极限锚固力，因此在开挖工程中锚杆支护这种形式是安全可靠的，此外由得到的云图可以了解锚杆的最大轴力一般出现在与衬砌想接触的地方，这使得施工的过程可以预知危险，可以再衬砌的地方进行喷锚技术，加固衬砌的稳定性.

另外由上面的ANSYS模拟得到的玉兔可以得到衬砌轴力的最大轴力一般出现在隧道拱的中央以及双连拱隧道连接的仰拱部位，这使得我们可以预知荷载最不利的地方的大概位置，从而在开挖的过程中给予施工过程的加固和监测.

5 结语

通过上述的ANSYS数值模拟，了解到公路双连拱隧道在开挖过程应力应变和内力的变化的最大值和最小值所处的位置以及支护结构锚杆的轴力分布情况，这样可以给施工提供很多不利因素的解决办法，达到提前预知危险源的作用.相信在未来的隧道开挖前一定也会经常采用这些有限元分析软件对隧道进行建模分析，这些分析得到的理论数据会给施工带来了诸多方便，例如采取什么样的支护结构等，这对未来施工有一定的指导意义.

参考文献：

〔1〕混凝土设计规范（GB50010-2010）.2015.

〔2〕杨伯源，张义同.工程弹塑性力学[M].北京：机械工业出版社，2014.

〔3〕陈秋南.隧道工程[M].北京：机械工业出版社，2017.

〔4〕李广信.土力学（第二版）[M].北京：清华大学出版社，2013.

〔5〕王新敏.ANSYS机构分析单元与运用[M].北京：人民交通出版社，2011.