Hirota方程的畸形波解和有理解

陈琪

摘 要：本文通过一般达布变换方法，构造了Hirota方程的一阶和二阶畸形波解和有理解，并通过图像比较了这两种解.另外，文章还对二阶畸形波解和有理解进行了分解.

关键词：Hirota方程;一般达布变换;畸形波解;有理解

中图分类号：O175  文献标识码：A  文章编号：1673-260X（2020）08-0001-03

0 引言

畸形波又称怪波，巨波，超级波等，是一种短时间内存在于局部区域的大振幅波动.它首先在海洋中被发现[1，2]，最早由Draper[3]提出，随后Smith[4]以非线性薛定谔方程为模型来研究海洋里的畸形波，它能够较好的描述畸形波的动力学特征.调制不稳定性被认为是畸形波产生的主要机理，另外孤子的碰撞也会产生畸形波[5].畸形波还广泛地出现在很多领域中，比如非线性光学[6，7，8]、Bose-Einstein凝聚（BEC）[9]、等离子体物理[10]、超流氦[11]、Capillary流[12]，还有经济[13]等很多方面.

本文旨在通过一般达布变换方法[14]构造Hirota方程的畸形波解和有理解，通过选取不同的参数值，得到了不同的解，并通过图像比较了一阶以及二阶畸形波解和有理解.之前也有其他作者用不同的方法对Hirota方程做过研究，也得到了一些很好的结论[15，16，17].

1 Hirota方程的一般达布变换

2 Hirota方程的畸形波解和有理解

2.1 一阶畸形波解和一阶有理解

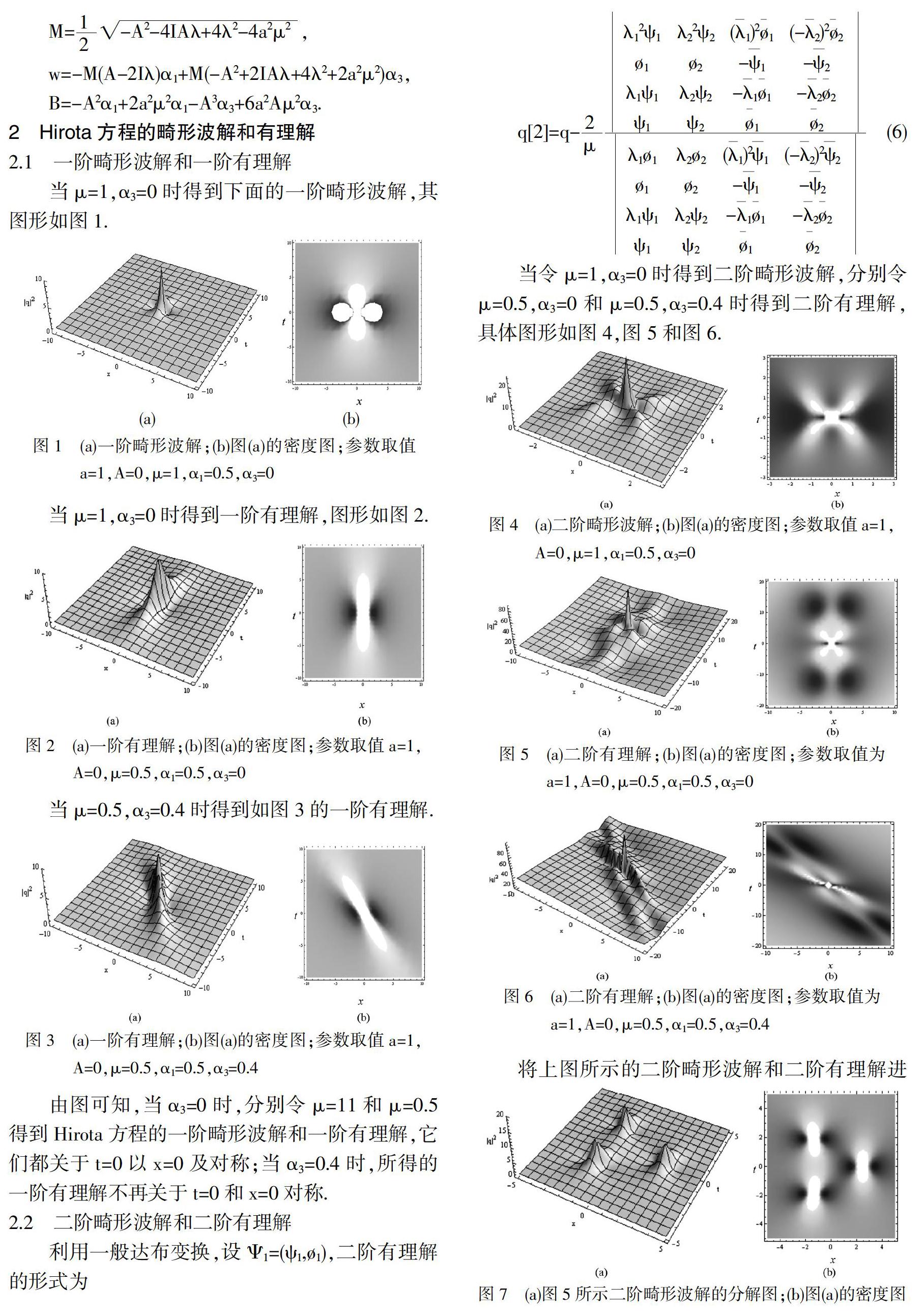
当？滋=1，？琢3=0时得到下面的一阶畸形波解，其图形如图1.

当？滋=1，？琢3=0时得到一阶有理解，图形如图2.

当？滋=0.5，？琢3=0.4时得到如图3的一阶有理解.

由图可知，当？琢3=0时，分别令？滋=11和？滋=0.5得到Hirota方程的一阶畸形波解和一阶有理解，它们都关于t=0以x=0及对称;当？琢3=0.4时，所得的一阶有理解不再关于t=0和x=0对称.

2.2 二阶畸形波解和二阶有理解

将上图所示的二阶畸形波解和二阶有理解进行分解（参考文献[18]）可得如下图7，图8和图9.

3 结论

本文对Hirota方程进行研究，通过一般达布变换方法求出了方程的一阶和二阶畸形波解和有理解，并且具体展示了它们的图形.文章通过选取不同的参数值，得到了不同的解，这对畸形波的传播控制研究有一定的参考价值.

参考文献：

〔1〕LIU P C. A chronology of freaque wave encounters [J]. Geofizika， 2007， 24（1）： 57-70.

〔2〕NIKOLKINA I， DIDENKULOVA I. Rogue waves in 2006-2010 [J]. Natural Hazards and Earth System Sciences， 2011， 11： 2913-2924.

〔3〕DRAPER L. ‘Freak ocean waves [J]. Oceanus， 1964， 10（4）： 13-15.

〔4〕SMITH R. Giant waves [J]. Journal of Fluid Mechanics， 1976， 77（3）： 417-431.

〔5〕DALFOVO F， GIORGINI S， PITAEVSKII L P， et al. Theory of Bose-Einstein condensation in trapped gases[J]. Reviews of Modern Physics， 1999， 71（3）： 463-512.

〔6〕SOLLI D R， ROPERS C， KOONATH P， et al. Optical rogue waves [J]. Nature， 2007， 450： 1054-1057.

〔7〕AKHMEDIEV N， DUDLEY J M， SOLLI D R， et al. Recent progress in investigating optical rogue waves [J]. Journal of Optics， 2013， 15（06）： 060201.

〔8〕胡文成，張解放，赵辟，楼吉辉.光纤放大器中非自治光畸波的传播控制研究[J].物理学报，2013， 62（02）：024216.

〔9〕BLUDOV Yu V， KONOTOP V V， AKHMEDIEV N. Matter rogue waves [J]. Physical Review A， 2009， 80（3）： 033610.

〔10〕RUDERMAN M S. Freak waves in laboratory and space plasmas [J]. European Physical Journal Special Topics， 2010， 185（01）： 57-66.

〔11〕GANSHIN A N， EFIMOV V B， KOLMAKOV G V， et al. Observation of an inverse energy cascade in developed acoustic turbulence in superfluid helium [J]. Physical Review Letters， 2008， 101（06）： 065303.

〔12〕SHATS M， PUNZMANN H， XIA H. Capillary rogue waves [J]. Physical Review Letters， 2010， 104（10）： 104503.

〔13〕YAN Z Y. Financial rogue waves [J]. Communications in Theoretical Physics， 2010， 54（05）： 947-949.

〔14〕GUO B L， LING L M， LIU Q P. Nonlinear Schr dinger equation： Generalized Darboux transformation and rogue wave solutions[J]. Physical Review E， 2012， 85（02）： 026607.

〔15〕ANKIEWICZ A， SOTO-CRESPO J M， AKHMEDIEV. Rogue waves and rational solutions of the Hirota equation[J]. Physical Review E， 2010， 81（04）： 046602.

〔16〕TAO Y S， HE J S. Multisolitons， breathers， and rogue waves for the Hirota equation generated by the Darboux transformation[J]. Physical Review E， 2012， 85（02）： 026601.

〔17〕LI L J， WU Z W， WANG L H， et al. High-order rogue waves for the Hirota equation[J]. Annals of Physics， 2013， 334： 198-211.

〔18〕CHEN Q， ZHANG W G， ZHANG H Q， et al. Rogue wave solutions for nonlinear Schr？dinger equation with variable coefficients in nonlinear optical systems [J]. Communications in Theoretical Physics， 2014， 62（03）： 373-382.