论学生思维参与的数学公式教学①——以“三角恒等变换”起始课为例

伍春兰 许文军

(1.北京教育学院 100120 ； 2.北京市第五中学 100007)

1 问题提出

数学公式背后隐藏着丰富的教育资源，适度的挖掘和利用，可达成更高的教育功能. 然而课堂观察发现，很多数学教师习惯于淡化公式的来源，简化公式的推导，重视公式的结构(记忆)和应用(解题). 仅靠规模化地知识应用(解题)的学习方式，于高考应试而言是高效的，但就思维训练来说则是欠缺的.此种现象，主客观的因素都有. 客观上高中三年知识两年赶完一年复习(甚至更长)，造成了新授课时的紧张.主观上，原因有三：教学观念偏差，系统设计不足，教材开采不够.

下面以高中“三角函数恒等变换”起始课为例，探讨如何系统设计，创设学生更多思维参与的教学活动.

2 系统设计

三角恒等变换，按照《普通高中数学课程标准(2017年版)》(以下简称《标准》)，包括和角、差角、倍角的三角函数(正弦、余弦、正切)公式，以及积化和差、和差化积、半角公式. 虽然后三组公式并不要求记忆，但六组公式，与之前学习的三角函数概念、两组公式(诱导公式、同角三角函数基本关系式)交织，成为了不少学生学习三角函数的噩梦. 面对公式众、变换 (角、名称、升降幂等)广 、联系密的学习内容，创设学生思维参与的构建知识网的活动才是王道.

2.1 “诱导”引入

现行普通高中数学人民教育出版社A版(以下简称人教A版)、人民教育出版社B版(以下简称人教B版)，北京师范大学出版社(以下简称北师大版)教科书，关于三角恒等变换，从内容顺序，到章/节头导言和情境，差异显见(表1). 与生活、社会有关的情境有益于学生应用意识的培养，但从承前启后的视角，我们更赞同人教A版的导言. 因为和、差角公式的认知起点是诱导公式，依从特殊到一般的思想，学生能自然进入和、差角公式的探究. 这样的引入，既经历了推理思考，也为学生形成三角函数公式的逻辑结构奠定良好的基础. 当然，现实情境与数学情境共进则是更妙的选择.

表1 各版教科书三角恒等变换章/节头导言和情境

续表

2.2 “多头”探究

现行教材遵从《标准》规定：经历推导两角差余弦公式的过程，由此推导其余的和角、差角、倍角的公式. 虽然各版本教材推导两角差余弦公式创设的问题情境(见表1)不同，但都直接指向两角差余弦. 需要思考的是：怎能想到先搞定两角差余弦，为什么不是两角和正弦，其它是否可以？

事实上，Cα-β，Cα+β，Sα-β，Sα+β四个公式，只需证明之一，就可借由诱导公式或变量代换推得另外三个. 即，四个公式谁领衔都不为过. 自上世纪50年代开始，教材经历了4次之变. 最早的教材是先证明Sα+β，70年代改Cα-β为首，90年代再改Cα+β为始.[1]自2003年《普通高中数学课程标准(实验)》颁布后，又回归到Cα-β. 可见，Cα-β，Cα+β，Sα-β，Sα+β谁为首席，教材编写者为学生操碎了心. 问题是学生领情吗？为此我们调研了上研究课的学生，问卷和统计结果见表2. 统计结果表明：近五成的学生首选和角作为先导，只有三成多学生将差角作为首选. 各组研究的顺序，基本上以正弦或余弦为始.

表2 学生调研统计

续表

考虑到学习者为北京市某示范高中校的数学优生，我们将和、差、倍角三组公式的整体“多头”推导，作为了三角恒等变换起始课的内容，不仅强化数形结合的逻辑推理，而且将三组公式纳入到相应的知识框架中，为灵活解决相关问题奠基.

3 合作探究

3.1 和差倍角何为首

教师请选择倍角为首的学生L发言：“倍角可看成两个角相加的特例，我原来想特殊到一般，现仔细一琢磨，倍角公式证明了，也无法直接应用到和角或差角上，还得再从头证明”. “也不是完全无用”教师总结道，“从特殊到一般是一种常用的研究方法，至少可让我们通过特殊的样态，推知一般的形式”.

经过比较，学生明确了由和角或差角出发研究均可，因为证明了和角或差角公式，经过换元或特殊化即可得到另外两组公式.

3.2 齐头并进谁争雄

至于选择哪个具体三角函数开始研究，毫无悬念地学生一致认可正弦或余弦函数. 于是根据前测，将学生分为四组探求公式，并确定了研究任务和顺序(表3).

表3 研究任务和顺序

3.2.1 起始公式的探究

4个组都无意间将α、β、α±β限制到锐角范围，不约而同地通过构造三角形，利用锐角三角函数的定义、相关三角形以及相关线段的关系等知识构造方程，得到相应的结论.

为什么要构建三角形？各组都回应了理由. 比如，“构造直角三角形，就能利用锐角三角函数的定义表示各边，然后利用三角形的等积变换以及相关三角形面积间的关系，列出以sin(α+β)为未知数的方程(图1)”“构造了含α、β、α-β的直角三角形，利用锐角三角函数的定义以及相关线段间的关系，列出以sin(α-β)为未知数的方程(图6)”“构造了含α、β、α-β的直角三角形，利用锐角三角函数的定义、勾股定理以及相关直角三角形间的关系，列出以cos(α-β)为未知数的方程(图7)”.

表4 初始公式证明

续表

续表

虽然探究有局限，但数形结合使学生对公式本质有了深刻认识，得到的公式结构为进一步严格证明指明了方向.学生在课后总结时说：“在解决问题时，要抓主要矛盾，当然选择策略也很重要！”“自己推导的公式，觉得特别清楚，印象深刻”.

图9

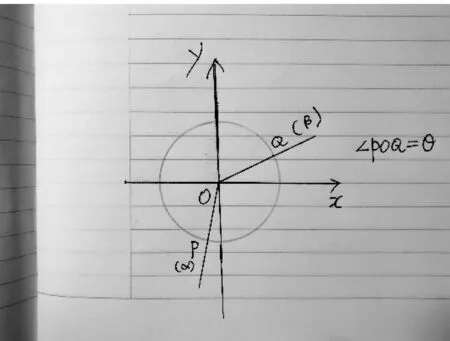
图10

学生刚学完向量知识，却没有人用此工具解决问题. 无论是想用因受阻而放弃，还是不熟悉而不愿意用，当他们用自己熟悉的构造三角形的方法和方程思想部分解决问题后，再回到向量方法，不仅找到了新旧知识之间的联系，而且也开阔了问题解决的视角，理解了现行教材以差角的余弦为始的用意，对向量作为工具的认识有了提升.

3.2.2 其余公式的探究

Cα-β，Cα+β，Sα-β，Sα+β作为起始公式分组证明后，学生推导同角的余弦或正弦公式的方法主要有三种：构造三角形、利用同角基本关系式、逆用诱导公式. 比较后，学生领悟到通过诱导公式可以充分利用已证明的公式，也省去了分类讨论的繁琐. 值得指出的是，逆用诱导公式，本质上是恒等变形(等式1). 学生在变形中，联想、转化、构建等活动，让他们体验到战胜挑战的满足，同时思维得到了锻炼.

=cosαcosβ-sinαsinβ.

等式1 采用诱导公由Sα+β推导Cα+β

当甲组的同学W亮出和角正切的推导过程及结果(等式2)时，乙组的一名同学质疑：能否只用两角的正切表示两角和的正切？见W有些迟疑，教师提示到：看看式子的结构.W喃喃到：“分子分母均为二次齐项式，分子分母可同除以cosαcosβ”. 于是他继续推导(等式3)，此时教室里响起了掌声，这该是对同学W独立思考的奖赏吧.

等式2Tα+β的推导过程1

等式3Tα+β的推导过程2

4 思考建议

4.1 先行组织者与逐步分化循序渐进

奥苏伯尔(D·P·AuSubel，1918-2008 )从学生获取信息的角度，提出了教学顺序：起点应先确定在学习层级的较高点，即先呈示一个一般的、有较大包容性的、较抽象的概念和原理，即所谓组织者. 由于组织者一般是在学习内容之前呈现的，故被称为先行组织者. 然后采用逐步分化原则，再学习一些具体的学习内容.[2]这一主张，为数学章节教学提供了一种思路，即整体——部分——整体. 首先章节的起始课，应构建“先行组织者”，为后续学习提供导航作用的知识框架，以及为思维参与提供支撑的思维支架. 其次章节的后续学习，采用逐渐分化的原则，体现了从整体到部分的认知过程. 最后章节的复习课，再次复盘“先行组织者”，既有利于新内容的学习，又能深化己有相关内容的理解．这样的教学顺序，与知识的组织方式契合，也符合学生的认知，有助于帮助学生形成良好的知识结构. 本节课的设计，正是构建“先行组织者”的起始课.

近几年，国内外学者进一步拓展了“先行组织者”的理论，提出“先行组织者”在包容性和抽象概括程度上既可以高于学习材料，也可以低于学习材料．[3]根据数学学科本身的系统性、逻辑性，从结构上说，“先行组织者”主要有上位组织者、下位组织者、并列组织者及类比组织者等.[2]

4.2 知识积累与思维训练并驾齐驱

杜威(Dewey，1859-1952)概括了思维的三种价值：有意识、有目的的行为的可能；系统化预测的可能；拓宽了客观事物的含义.[4]前两者属于实际价值，能让学生更好地遇见当今或未来的社会生活；而第三种价值，在于让学生精神世界的丰盈. 本课例起始公式的探究中，教师创设“多头”探究活动，以及放手让学生在数与形的构建中分组遨游，没有牵引学生直接应用解析几何及向量工具快速证明，其意义在于既重视实用思维的价值，更尊重学生的认知起点，关注其学科价值的充实. 实践表明只有在充分思维训练过程中获得的知识，才是“活”的、能得以有效运用的知识.