波浪条件下刚性植被茎干紊流对沉积物再悬浮的促进作用*

易雨君，唐彩红，张尚弘

(1：北京师范大学水环境模拟国家重点实验室，北京师范大学环境学院，北京 100875) (2：华北电力大学水利与水电工程学院，北京 102206)

水生植被广泛分布于河流、湖泊以及滨海湿地等浅水域中，为鱼类、底栖动物和其他水生动物提供食物和栖息地[1-3]. 水生植被可以吸收水体过剩营养物质，净化水质改善透明度；通过植物根系稳定河床保护河岸；还可衰减波浪，避免海岸带遭受侵蚀[4-5]. 在浅水域，沉积物易受风生波影响导致再悬浮，加剧悬浮颗粒中营养物和污染物的释放，从而导致水体营养物质的增加以及水质恶化[6]. 太湖的原位观测实验表明，太湖底泥沉积物再悬浮的临界剪切应力为0.03～0.04 N/m2，风生浪是导致太湖底泥沉积物再悬浮的主要驱动力，当风速达到6.5 m/s时，沉积物再悬浮含量以及水体氮磷营养物质浓度会急剧增加[6]. 一方面，水生植被可以有效削减波浪并降低近床面波速[7-8]，从而减少波浪驱动的沉积物再悬浮[9]；另一方面，有研究表明波浪与植被的相互作用能增强近床面的紊流[10-11]，而紊流的增加能增强沉积物的再悬浮作用. 研究发现，柔性沉水植被的刚性叶鞘具有与挺水植被类似的性质，刚性叶鞘部分产生的近床面紊动能与波浪轨道运动半径(Aw)和植株间距(S)的比值(Aw/S)有关，当Aw/S> 0.5时，相比无植被情景，植被能有效增加近床面紊动能[11]. 随机排列的红树林模型植被实验结果表明，波浪驱动的沉积物悬浮浓度与紊流强度之间存在正相关关系，再悬浮的临界波速在植被层内相对于光滑床面更低，其原因在于植被产生的紊流作用促进了沉积物再悬浮[12]. 当植被产生的紊流强度增加了近床面的总紊流强度时，沉积物悬浮浓度也随之增强[13]. 相比实验室研究，田间尺度上密集的鳗草冠层内波浪速度和紊流的减少，反过来减少了沉积物再悬浮[14]. 同样，在浅水湖泊中，与无植被区域相比，沉水和挺水植物的存在使滇池福宝湾生态恢复区的底泥再悬浮量、氮磷释放量均削减了80%以上[9]. 田间观测和实验室观测之间互相矛盾的结果反映了植被对波浪衰减[15]和紊流形成的双重影响[11]. 即是植被产生的紊流可以局部增强沉积物再悬浮作用[12-13]，但是大面积植被的波浪衰减可以有效减少沉积物的再悬浮[14]. 本研究以植被茎干产生的紊流可局部增强沉积物再悬浮为切入点，旨在阐明波浪条件下刚性植被茎干产生的紊流如何影响沉积物再悬浮过程，提出沉积物再悬浮植被紊流模型，基于该模型预测沉积物再悬浮的临界波速，通过水槽试验的实测数据对该模型进行验证，并将其扩展到其他研究中.

1 植被紊流与临界波速的理论关系

植被产生的紊流涡旋将能量从平均流场转移到紊流中，单向水流中非淹没刚性植被产生的紊流模型ktv可表示为[16]：

(1)

式中，U为空间和时间平均的纵向速度，CD为植被拖曳力系数，φ是植被固相体积分数，δ为比例因子. 对圆柱形植被茎干而言，φ=mπd2/4，其中m为植被茎干密度(根/m2)，d为植被直径. 公式(1)适用于d/S<0.56 的植被情景.

研究表明，近床面总紊动能(kt)可表示为植被产生的紊动能(ktv)与床面产生的紊动能(ktb)之和，即是kt=ktv+ktb[17]. 在光滑床面的单向流动中，ktb与水流产生的床面剪切应力τc之间存在线性关系，已有研究证实光滑床面τc/ρktb=0.19[18]. 此外，床面剪切应力可以根据流速U和床面摩擦系数Cf估算，即τc=ρCfU2，使得ktb=CbU2，其中Cb≈Cf/0.2. 结合公式(1)，单向流中近床面总紊动能可表示为：

(2)

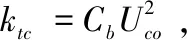
(3)

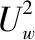
将公式(2)中的流速替换为波速，可得波浪驱动下的植被紊流方程为：

(4)

(5)

2 实验设计与方法

根据2016年对白洋淀春、夏、秋3个季节12个采样点的水生植被野外采样(图1a)，S1～S12分别为东关码头、鸳鸯岛、淀头、端村、采蒲台、圈头、枣林庄、光淀张庄、王家寨、大口子、烧车淀以及旅游码头. 结果显示，白洋淀挺水植被以芦苇和香蒲为主，芦苇株高为2.70±0.33 m，株茎为0.77±0.15 cm，沉水植被以金鱼藻、菹草、眼子菜科为优势种. 同时采集12个采样点的沉积物，将其带回实验室物理风干后用激光粒度分析仪(Microtrac S3500 Particle Size Analyzer)进行粒径测量. 结果表明，白洋淀12个采样点的沉积物平均中值粒径D50=0.076 cm，属于细砂，各采样点的沉积物粒径分布见图1b. 相比较而言，白洋淀沉积物粒径大于太湖(D50=0.009 mm)、龙感湖(D50= 0.007 mm)以及巢湖的湖岸(D50=0.007 mm)和湖中心(D50=0.010 mm)[21].

图1 白洋淀采样点分布(a)，不同采样点的沉积物颗粒级配曲线(b)Fig.1 Distribution of sampling sites in Lake Baiyangdian(a)，accumulative percentage of sediment size of different sampling sites(b)

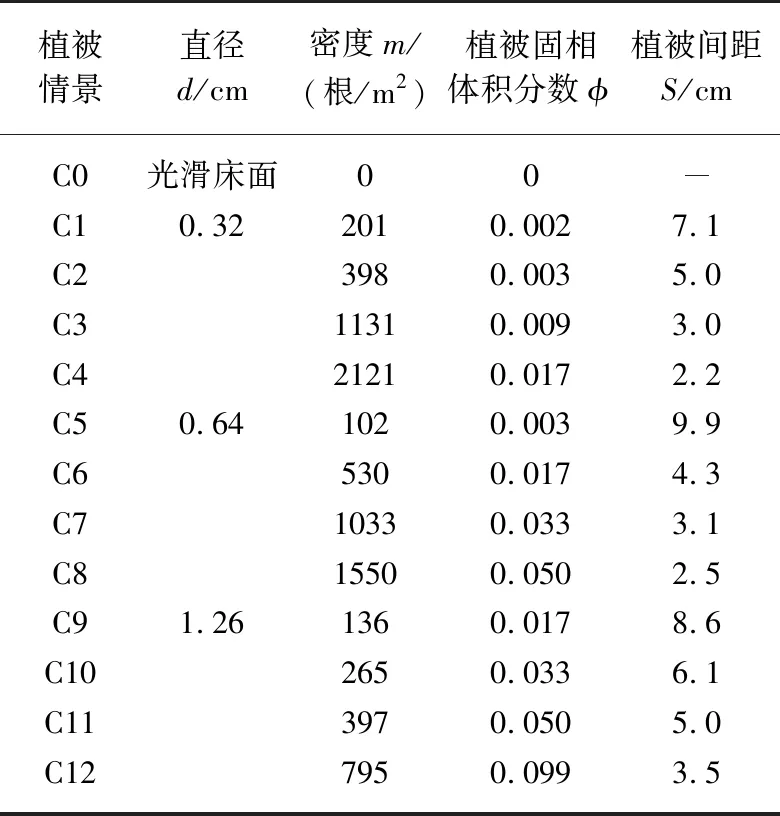
表1 波浪水槽试验参数设置

图2 波浪水槽以及植被铺设示意Fig.2 Schematic of wave channel and vegetation experiments

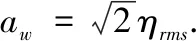
波浪的瞬时速度u(t)可分解为时均流速Uc、震荡的波浪流速Uw(t)和紊动流速u′(t)(以u为例，对于v和w相同)：

u(t)=Uc+Uw(t)+u′(t)

(6)

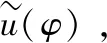
(7)

(8)

本文以TKE表示波周期内所有相位的时间平均的实测紊动能，以kt表示植被紊流模型的计算紊动能. 运用光学后向散射浊度仪(OBS，Seapoint Sensors Inc.)测量悬浮颗粒浓度，将其放置于植被层纵向和横向中间位置，浊度仪探头位于沙床上方5 cm处，探头朝下. 每个波浪情景下，浊度仪以20 Hz的采样频率连续采集10 min，将电压输出结果转换为悬浮颗粒浓度.

3 结果与讨论

3.1 植被紊动能

对于单向流，淹没植被层顶部阻力不连续，通过剪切层不稳定性产生紊流相干结构，并在冠层顶部产生紊流峰值[24]. 相比较而言，在波浪情景下，只有长波(T> 12 s)流经密度较大的植被层时会在冠层顶部产生剪切层不稳定性[25]. 本研究所采用T=2 s的波浪情景未产生紊流相干结构，故仅考虑植被茎干产生的紊流.

图3 不同植被情景下的近床面紊动能TKE和的关系Fig.3 Relationship between measured near-bed turbulent kinetic energy and within vegetation canopy

对于单一直径的植被(d=0.32、0.64或1.26 cm)，植被茎干φ越大所产生的TKE越大(图4). 对于相同的φ，直径仍然影响TKE，尤其是对于直径较大的植被，如φ=0.017和0.05，相同φ不同直径所产生的TKE差异更大. 在图4b, c中，植被固相体积分数φ=0.017的3种直径的植被层产生的TKE相近，但当φ=0.05时，直径d=0.64 cm(图4b)和d=1.26 cm(图4c)的植被层所产生的TKE则存在明显差异. 此外，当波浪轨道运动半径与植被间距的比值Aw/S越大时(Aw=UwT/2π)，刚性植被茎干所产生的紊动能越大，尤其是当Aw/S≥ 1时，植被茎干产生的紊流可以传播到整个植被层，前人对沉水植被刚性叶鞘的研究也揭示了同样的结果[11]. 而对于Aw/S< 0.5，本研究中茎干产生的紊流与前人研究中[11]光滑床面产生的TKE相当，Zhang等的结果是基于φ=0.011～0.051[11]，该植被φ范围小于本研究中的φ范围(φ=0.0016～0.099). 本研究中的Aw/S=0.16～3.21(图4)，当Aw/S> 1时，植被阻力主导水流，导致冠层内的波速小于冠层外；相反，波的传播与主导惯性力有关，在Aw/S< 1的情况下冠层内的速度会变大[13]，这表明植被所产生的TKE将根据Aw/S的不同分为两部分.

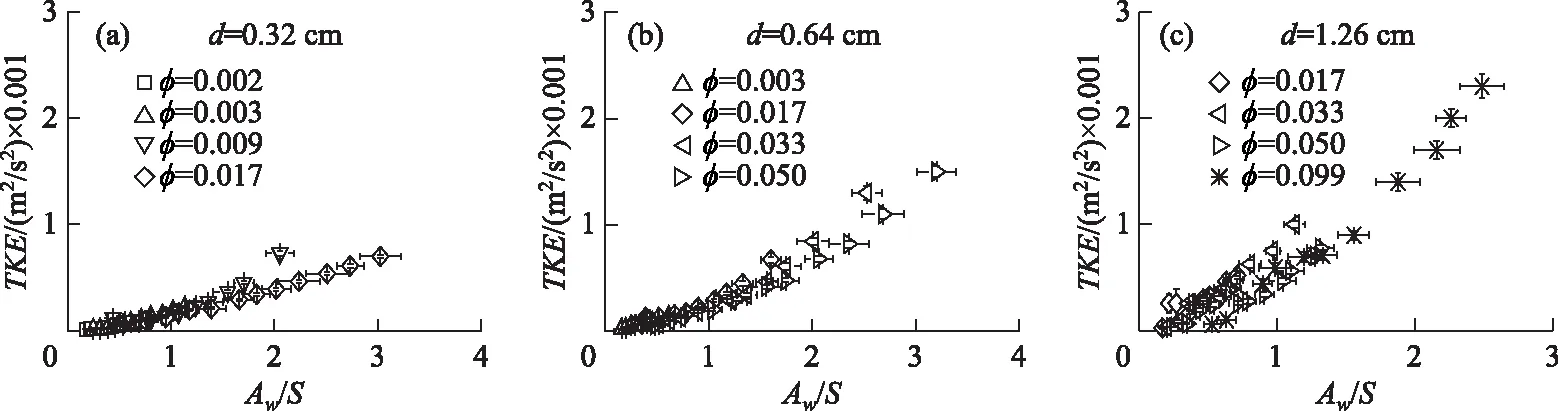
图4 实测植被层近床面紊动能TKE与Aw/S的关系Fig.4 Relationship between measured near-bed TKE and Aw/S

为确定植被紊流模型中紊流的比例因子δ2，将实测TKE与紊流模型预测值(公式(4)等式右边第一项)进行比较，比较结果如图5所示. 从图3可知，φ=0.002和0.003的植被层具有与光滑床面(φ=0)相近的紊流水平，因此图5中不考虑φ=0.002和0.003的植被产生的紊动能. 植被阻力系数CD根据Keulegan-Carpenter数[26](简称KC数，KC=UwT/d)估算，得到3种直径的植被阻力系数CD=1.5±0.3. 实测紊动能与公式(4)中植被紊动能的预测值的线性拟合的斜率为δ=0.78±0.02(95%CI)，即紊流比例因子δ2=0.61±0.02.

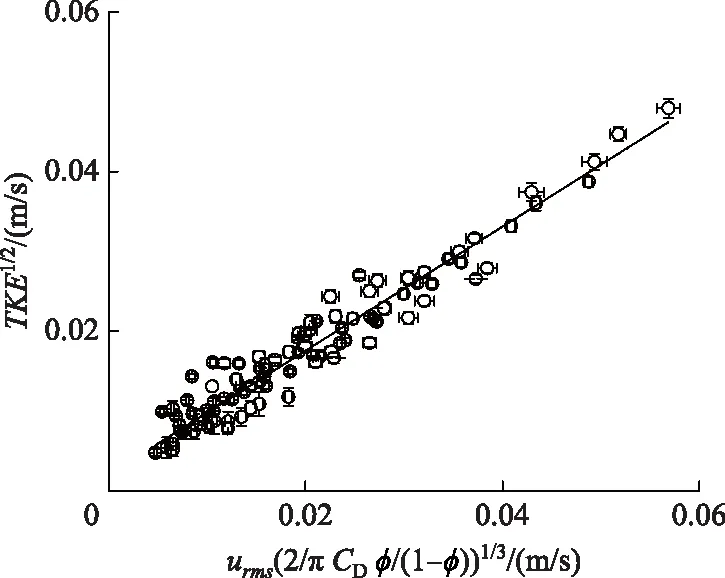
图5 近床面紊动能实测值与植被紊流模型计算值对比Fig.5 Comparison of measured near-bed TKE with predicted vegetation-generated turbulence

3.2 沉积物再悬浮浓度与临界速度

沉积物再悬浮浓度受植被固相体积分数和波浪条件共同影响，用φ表示直径和密度的影响(图6). 当悬浮颗粒平均浓度高于OBS仪器噪声水平时，则认为沉积物开始悬浮，此时的波速为沉积物再悬浮的临界波速，仪器噪声水平即是不同植被情景下静水时测量浓度的平均值，为7 mg/L. 本研究所用的模型沙的沉降时间为沙子在OBS测量深度(h′=5 cm)上的标准化沉降速度，即沉降速度ws=0.4 cm/s，沉降时间h′/ws=1.25 s. 对于已经悬浮的颗粒沙，沉降时间小于波浪周期(T=2 s)，表明部分颗粒在较小的波浪条件下沉降.

除密度较小的植被情景(φ=0.002和0.003)外，其余植被情景下沉积物再悬浮的临界波速小于光滑床面的临界速度值，一旦沉积物重新悬浮，相同的波速下，悬浮浓度随植被固相体积分数φ的增加而增加(图6). 该结果表明，在大多数植被情景下，与光滑床面相比，植被的存在增强了沉积物再悬浮. 同样的结果也曾被报道：悬浮浓度受到固体体积分数φ的影响，且具有较大φ的植被情景下沉积物再悬浮时间更早[27]. 在直径更大(d=2 cm)的模型植被层中，单向水流下的沉积物再悬浮浓度随φ的增加而增加[28]. Tinoco和Coco[12]也阐明了植被层中的沉积物再悬浮浓度随φ(φ=0、0.008、0.047、0.079)的增加而增加这一类似结论，在波浪扰动下，植被产生的紊动能比床面切应力更能促进沉积物再悬浮.

图6 沉积物再悬浮浓度与urms之间的关系Fig.6 Suspended sediment concentration as a function of wave velocity (urms)

所有直径的植被层中沉积物再悬浮临界速度urms,c随固相体积分数φ的增加而降低(图7)，由此可知，φ对沉积物再悬浮的重要性高于植被直径d，这一试验结果与植被茎干产生的紊流控制沉积物再悬浮理论一致(公式(4)右边第一项). 因此，本研究将圆柱形植被层影响下的沉积物再悬浮临界速度的观测范围限定在植被直径d=0.32～1.26 cm.

图7 不同直径植被下沉积物再悬浮临界速度与植被固相体积分数Fig.7 Critical velocity for wave-driven resuspension within arrays of circular cylinders of diameter d versus solid volume fraction φ

光滑床面所测量的沉积物颗粒(D50=85±21 μm)再悬浮的临界速度均值为urms,co=9.1 cm/s，则光滑床面沉积物再悬浮临界状态的最大波速即是轨道波速Uw= 12.8±0.9 cm/s. Shields数 (θ=τb/(ρs-ρ)gD50)与颗粒粒径相关，可用于确定颗粒运动的临界状态，当θ值大于临界θ时，可认为是沉积物再悬浮的初始状态[29]. 由此可知，小颗粒的再悬浮临界速度较低. 遵循Yang等[17]与Tinoco 和 Coco[12]的结论，植被产生的紊流是沉积物颗粒起动和再悬浮的主要驱动因素. 图8比较了悬浮颗粒浓度和近床面的紊流水平，在大多数直径情景下(d=0.32、0.64、1.26 cm)，沉积物悬浮颗粒浓度在TKE≈3×10-4m2/s2时高于测量仪器噪声水平7 mg/L(图8中的黑虚线). 已有研究发现在d=2 cm的随机植被分布格局中，波浪扰动的植被情景下，沉积物再悬浮的植被紊动能阈值TKE≈ 6×10-4m2/s2[12]. 此TKE阈值略大于本研究中的阈值(TKE≈ 3×10-4m2/s2)，其原因是该文献研究使用的沉积物颗粒(D50=280 μm)稍大于本研究(D50= 85±21 μm).

图8 不同植被情景下沉积物悬浮物浓度与近床面紊动能之间的关系Fig.8 Suspended sediment concentration as a function of near-bed turbulent kinetic energy for cylinder diameters (a) 0.32 cm, (b) 0.64 cm, and (c) 1.26 cm

所有试验情景中有4种情景的沉积物再悬浮临界紊动能低于前文所述的临界水平(3×10-4m2/s2)，分别是光滑床面(φ=0)、直径d=0.32 cm的φ=0.002和φ=0.003(图8a)，以及直径d=0.64 cm的φ=0.003(图8b). 可能的原因是，对于光滑床面和φ值较低的情景，床面产生的紊流是近床面总紊动能的最主要来源. 因此，在推求沉积物再悬浮的临界紊动能时，不考虑上述4种情景的TKE. 根据其余植被情景得到沉积物再悬浮的临界紊动能kt,c=2.6±1.0(×10-4m2/s2)，其中kt,c的不确定性为不同植被情景的标准偏差.

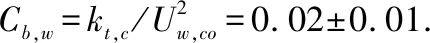
图9 沉积物再悬浮临界波速实测值与模型预测值Fig.9 Comparison of predicted and measured critical wave velocity

本研究仅考虑具有单个周期(T=2 s)的波，对应野外的风生波，可近似于例如大型浅水湖泊太湖风生浪的波浪周期T= 1.2～1.8 s和波高(2 cm和10 cm)[30]. 但本文提出的植被紊流模型可能不适用于流经植被层的长波，长波会在植被冠层顶部产生剪切紊流，并有助于再悬浮[25]，如受海洋重力波等长波影响的潮滩植被. 此外，本研究所提出的波浪驱动下刚性植被层中沉积物再悬浮模型，可与植被影响下的波浪衰减模型相结合，综合考虑植被层对波浪的衰减和沉积物再悬浮的抑制作用，以及植被茎干产生的紊流对沉积物再悬浮的促进作用，以此得到实际野外波浪扰动下植被对沉积物的综合影响，并得出基于沉积物沉降或再悬浮需求的适宜植被面积、植被密度和高度等分布特征，为浅水湖泊和滨海湿地生态修复与保护提供科学指导与关键参数.

4 结论