I&I自适应的STATCOM与发电机励磁鲁棒协调控制

杜超凡,张 蕾,孙崧强,朱家豪

(西安工程大学 电子信息学院,陕西 西安 710048)

0 引 言

我国电网是以大规模、大机组、超高电压、远距离传输及高度自动化等为发展特征,电网的互联特性使得系统的稳定性问题显得尤为重要[1-2]。柔性交流输电系统(flexible AC transmission systems, FACTS)作为有效提高电网互联稳定性的先进技术之一,是国内输电网络中维持电压稳定的重要装置[3-4]。STATCOM作为一种FACTS装置,具有改善电压质量、调节无功功率、提高系统暂态稳定性等性能[5-6]。另一方面,发电机励磁对解决系统稳定性问题具有显著的优势[7-9]。因此,研究STATCOM与发电机励磁的协调控制系统极具价值和意义。

近年来,国内外学者在STATCOM与发电机励磁协调控制方面做了许多研究。文献[10]应用Hamiltonian能量方法设计了发电机励磁与STATCOM的协调控制方法,并以多机系统为例进行验证,保证了电力系统的稳定性,但未考虑系统中不确定参数对系统稳定性的影响。文献[11]在无源性理论的基础上采用反步法逆推设计控制律,但未考虑在遭受未知扰动时,发电机端电压的稳定性。另外,相关文献还采用了其他控制理论,包括目标全息反馈法[12]、模糊控制[13]、自适应反步法[14-15]等。这些控制方法使STATCOM与发电机励磁系统的控制性能进一步加强。自适应反步法作为一种处理非线性系统控制问题的有效工具,广泛应用于具有典型非线性特性的电力系统,并取得了较好的效果。但自适应反步法对系统中参数估计依赖于确定性-等价原理,要求系统满足下三角结构。为此引入了文献[16]提出的I&I自适应控制方法,设计了一种新型的模块化参数自适应方法,不依赖于传统自适应方法中的确定性-等价原理,在参数估计误差构造时,引入非线性可调函数使得参数自适应律的设计更加灵活可控,有效提高了参数自适应辨识能力。

综上所述,针对STATCOM与发电机励磁的协调控制系统中存在阻尼系数不易精确测量和未知扰动难以处理的问题,设计了I&I自适应鲁棒协调控制方法。采用I&I自适应控制法设计参数自适应律;在反步法设计控制律过程中,采用已设计的参数自适应律,并根据L2-增益抑制理论来定义能量函数,从而消除未知扰动对于系统暂态稳定性的影响。在参数摄动和未知扰动发生的情况下,保证了发电机功角和STATCOM接入点电压的暂态稳定性。

1 系统模型

本文考虑如图1所示装设STATCOM的单机无穷大电力系统(single machine infinity system, SMIB)。发电机经过变压器与带有短路器的输电线路相连,STATCOM装设在线路中点处,这也是能有效提高系统输电容量、延长输电距离的最佳接入点[17-18]。本文所提STATCOM与发电机励磁自适应鲁棒协调控制方法包括励磁控制律uf、STATCOM控制律us及参数自适应律的设计。

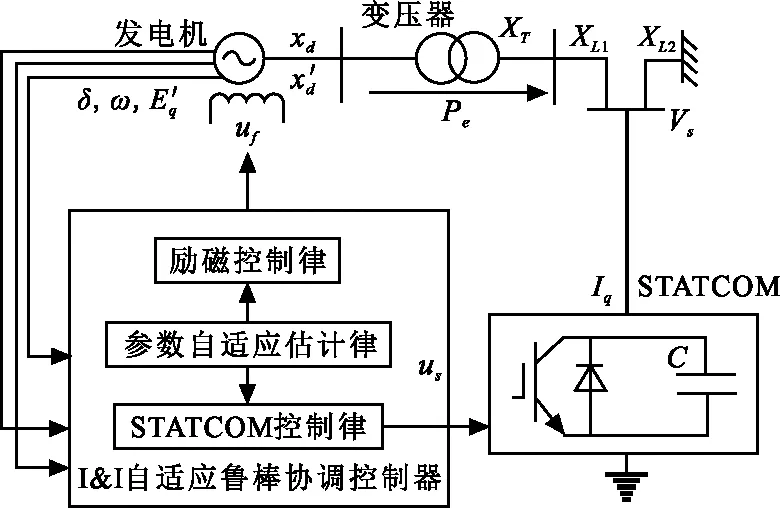
图 1 装设STATCOM的SMIB系统Fig.1 SMIB system with STATCOM

采用文献[11]所用的模型,发电机励磁采用3阶模型,STATCOM采用1阶电流源模型。假设如下:①发电机的机械功率Pm为常数;②不考虑调速器的作用。在此基础上,建立图1中STATCOM与发电机励磁系统的状态方程:

(1)

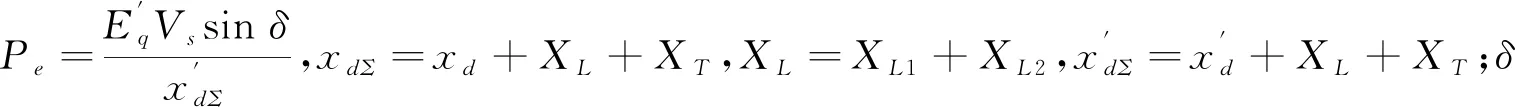
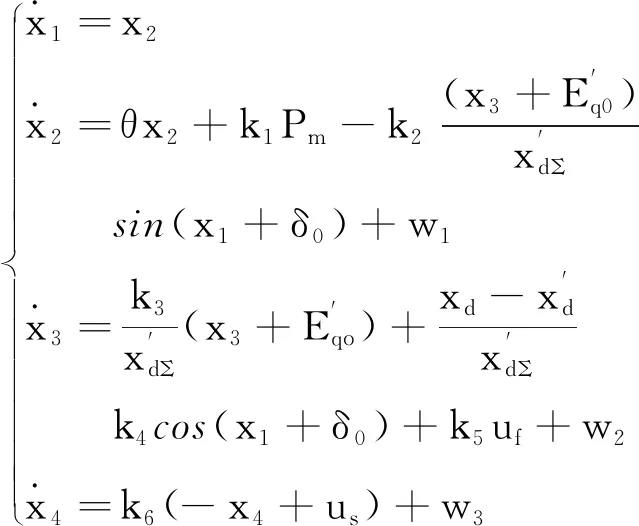
(2)

假设系统的调节输出为y=[q1x1q2x2]Τ,其中q1、q2分别为x1+x2的非负加权比重系数,且满足q1+q2=1。

控制目标:在考虑系统中参数不确定且遭受未知扰动的情况下,设计自适应律来辨识不确定参数θ,并通过反步法设计控制律uf、us使系统在遭受扰动时,状态变量x1、x2、x3、x4不会失去同步而导致系统失衡,在扰动发生后,所有状态变量暂态响应曲线有界且稳定运行于某一平衡点。

2 I&I自适应鲁棒协调控制设计

2.1 参数自适应律设计

采用I&I自适应控制法为系统中不确定阻尼系数设计参数自适应律。首先,定义参数估计误差为

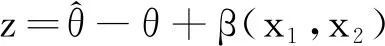
(3)

(4)

由于满足wi≤hi,设计参数自适应律为

(5)

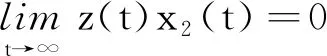
2.2 鲁棒协调控制器设计

首先,将高阶系统降阶成4个低阶子系统;然后,采用反步法推导励磁控制律uf、STATCOM控制律us,并根据L2-增益抑制理论来定义扰动输入的能量函数;最后,根据耗散理论证明所设计的方法能保证系统具有鲁棒抑制能力[20]。

定义系统的状态误差函数为

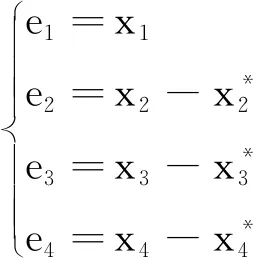
(6)

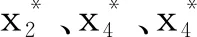
步骤1:对上述定义的第1个系统状态误差e1求导得

(7)

步骤2:对上述定义的第2个系统状态误差e2求导得

(8)

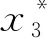
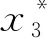
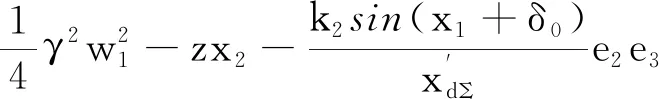
(9)

步骤3:对上述定义的第3个系统状态误差e3求导得

(10)

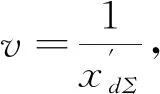
(11)

为消除前3阶子系统中未知扰动w1和w2对输出系统暂态定性的影响,定义第2个能量函数为H2,将调节输出y和式(11)代入,可得

(12)

步骤4:根据整个系统(2)构造新的状态变量,将设计虚拟控制律为

对上述定义的第4个系统状态误差e4求导得

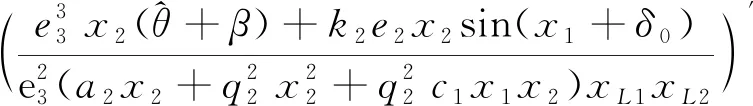
(13)

将STATCOM控制律us设计为

(14)

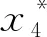
(15)

2.3 系统稳定性证明

引理1[20]令γ≥0,∀T≥0,STATCOM与发电机励磁的协调控制系统在uf、us控制律的作用下,闭环协调控制系统满足如下耗散不等式成立:

(16)

式中：V(·)是系统(2)的储存函数,则称系统(2)具有L2-增益且小于γ。

根据引理1,令储存函数V=V4,将两边进行积分可得

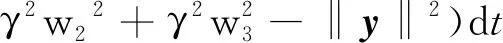
(17)

由式(17)可知,在系统遭受未知扰动的情况下,具有L2-增益抑制能力。LaSalle-Yoshizawa定理可知,所设计的参数自适应律,励磁控制律和STATCOM控制律使得闭环系统中的状态变量x1、x2、x3、x4都是一致有界的,且渐近稳定。

3 仿真验证

为验证本文所设计的I&I自适应鲁棒协调控制(adaptive coordinated control, BACC)方法在系统稳定性方面的控制效果,在Matlab/Simulink环境下,将所设计的方法与参考文献[12]中基于传统自适应反步协调控制(traditional adaptive backstepping coordinated control, TABCC)方法在相同运行情况下进行仿真分析。

系统初始工作在稳态平衡点,假设系统在t=0.1 s时,输电线路上STATCOM接入点在母线左侧发电机的输电线路中发生短路故障,经0.1 s切除故障后,将本文所设计的BACC方法与TABCC方法进行仿真对比。

x1(发电机的功角)和x2(发电机的角速度)的暂态响应曲线分别如图2和图3。

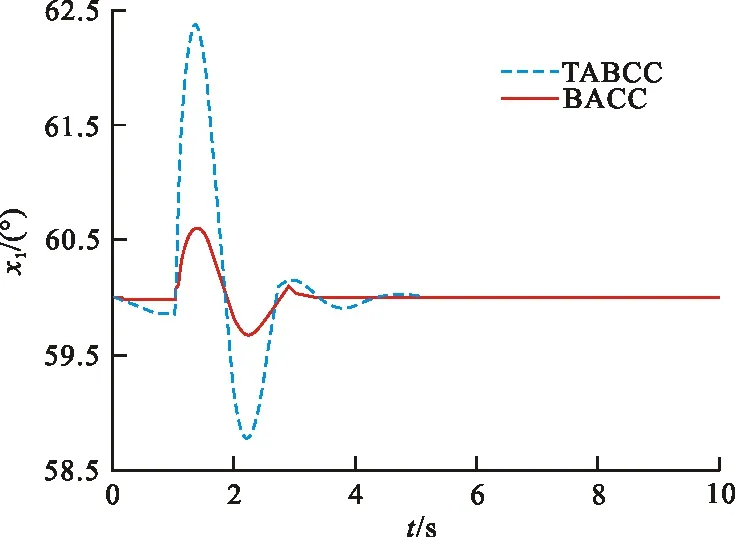
图 2 状态变量x1的暂态响应曲线Fig.2 Transient response curve of state variable x1

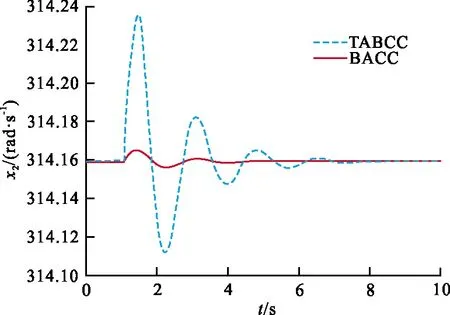
图 3 状态变量x2的暂态响应曲线Fig.3 Transient response curve of state variable x2

由图2～3可知,在输电过程中发生扰动后,在BACC方法的作用下,发电机功角的暂态响应曲线振荡幅值小,且减少了40%左右;发电机角速度的暂态响应曲线振荡幅值小且时间短,将扰动后的过渡过程缩短了3 s左右。

x3(发电机的暂态电势)和x4(STATCOM接入系统的等效电流)的暂态响应曲线如图4和图5。由图4～5可知,在发生扰动后,相比于传统的TABCC方法,发电机暂态电势的暂态响应曲线振荡范围小,且能很快恢复到故障前的运行状态;STATCOM接入系统的等效电流的暂态响应曲线开始振荡不明显,但在运行2 s之后,振荡幅值明显减小且5 s后就逐渐稳定。

图6为不确定参数θ的响应曲线图。由图6可知,所设计的BACC方法,只需0.1 s左右,即可以迅速地将估计值稳定在-0.17,且与所设置的真值基本一致,故可得基于I&I自适应控制方法所设计的参数自适应律能够有效辨识不确定参数,提高参数的自适应能力。

图 4 状态变量x3的暂态响应曲线Fig.4 Transient response curve of state variable x3

图 5 状态变量x4的暂态响应曲线Fig.5 Transient response curve of state variable x4

图 6 不确定参数估计响应图Fig.6 Estimated response curve of uncertain parameters

4 结 语

本文通过I&I自适应鲁棒协调控制方法对系统中参数自适应律、励磁控制律和STATCOM控制律进行设计,提高了系统中参数自适应辨识能力,同时增强了系统的鲁棒性。在设计过程中,将参数自适应律和控制律分开设计,不需要在反步法中递推地构造含参数估计误差的状态变量,从而避免了反步法中存在的“计算膨胀”和“过参数化”问题。仿真结果表明了所设计的BACC方法能有效改善系统的暂态性,保证了发电机功角、转子角速度等输入变量在所设计的控制方法下都具有良好的暂态性能。