基于耦合方程的系泊系统浮动区域状态研究

王 帅

（长春光华学院基础教研部，吉林 长春 130033）

0 引言

在潮汐等因素的影响下，考虑风力、水流力和水深对系统的影响，海上系泊系统为一个多自由度的耦合系统运动，首先建立起海上系泊系统对风力、水流力和海水深度的不同情况进行假设，对钢管的静平衡进行分析，通过不同情况的数据分析，利用耦合方程得出不同情况下钢桶钢管游动区域。并且在如下的条件基础上找出浮标游动距离与风速、海水速度、水深的关系。

1 系泊系统耦合方程

当系泊系统在海上作为刚体做六个自由度的振荡运动。系泊系统的六个自由度的运动是互相关联即耦合运动。 因此，考虑系泊系统在海上运动应考虑其耦合影响。

两自由度耦合运动是最简单的多自由度耦合系统。 所以对于多自由度耦合运动系统的讨论，首先从两自由度系统运动系统开始，并加以推广。

由达朗贝尔方程：

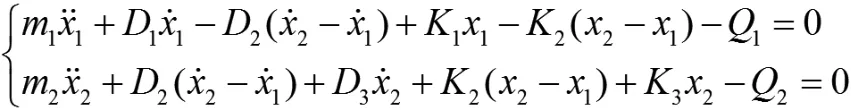
可以推出：

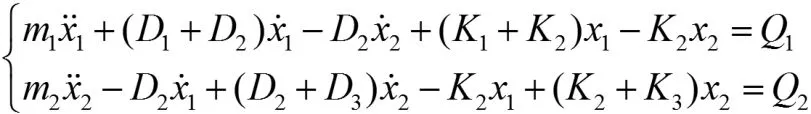
其中：

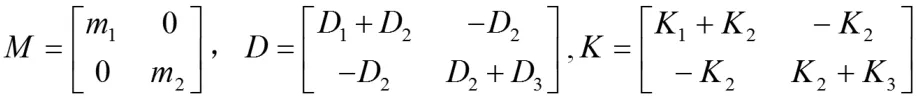
2 海上系泊系统漂浮模型

当浮标受风力和潮汐等因素的影响，会在一定范围内产生漂移。一段时间后，由于钢管、铁桶和锚链对浮标的牵引作用，整个系统将处于静平衡状态。

海上系泊系统受力为，T 为下方钢管给予浮标的拉力，φ 为拉力T 的倾角，Fa为风力作用在浮标上产生的水平力，Fc为海水流动作用在浮标上的水平力，Mg为浮标的重力，FB（θ，h）为水给予浮标的浮力，h 为浮标的吃水深度。

设Ma为风引起的对过浮标中心轴的力矩；Mc为海流引起的对过浮标中心轴的力矩xc，zc为钢管在浮标底部系点与浮标重心的水平及垂直距离，la（θ，h）为风力中心与浮标重心的距离。 其中， 可知Fa=0.625×Sv2，可得 Ma=Fala（θ，h）。同理，由 Fc=374×Sv2，可得 Mc=Fclc（θ，h）。通过受力平衡可以得到：Fa+Fc=Tcosφ，FB（θ，h）

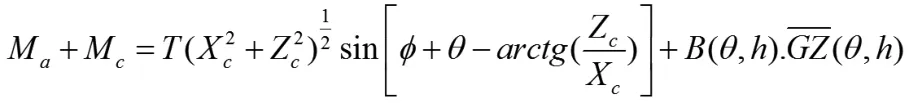
综上所述，未知量T、φ 与下方钢管及重物球的悬挂状态有关，因钢管为4 节，所以从海平面逐个依次向下积分。

钢管的受力情况分析，其中T 为拉力，dT 表示ds上的拉力变化，dφ 表示在拉力变化作用下产生的倾角变化。F 为单位长度上的法向流拖曳力；G 为单位长度上的切向流拖曳力；Vc为流速。

根据数据，钢管每根长1 m，重10 kg，即钢管单位长度重量为10 kg，根据平衡关系：

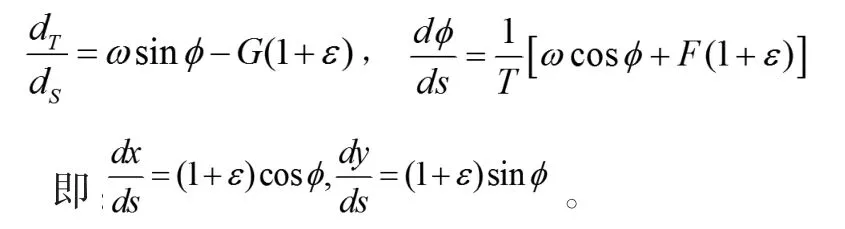
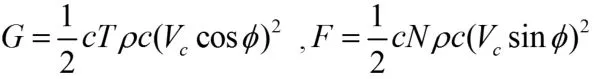
将上述方程整合，得到一组微分方程，根据上面对浮标的分析，先假定一个h，带入钢管微分方程计算，若结果不成立则重新假定，最终用逐步近似法得出符合条件的解。

3 锚链形状及浮标游动区域

设系泊点离海底距离H0，刚拉起锚链长S0，触底长度为L0，浮标在海风的作用下发生游动，此时投影长度为X，锚链形状为L，则根据悬线理论解得：锚链形状（卧链长度）变化：ΔL=L0-L，可得漂移区域：E=XX0-ΔL=9.78。 海水深度为 16～20 m，此时分别取海水深度为16 m～18 m 和20 m 进行研究，由数据可知，假设海水速度最大可达到1.5 m/s， 风速最大为36 m/s，即取海水速度区间[0，1.5]m/s，取风速[0，36]m/s 进行研究。 此时，浮标受风力和海水作用力的影响发生倾斜，通过受力分析可得：

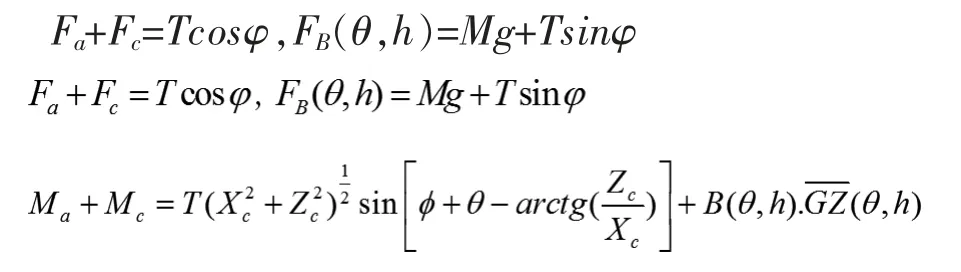
根据钢管平衡关系可知：

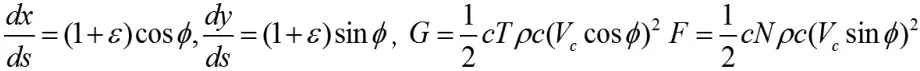
通过逐步近似法， 得出各变量之间关系如图2所示。

4 结论

本文首先建立了海上系泊系统的耦合方程，并对方程加以分析，在此基础上运用分段外推法对海上运动系统进行求解，求解出其在海上浮动区域的倾斜角度、吃水深度和具体的浮动区域范围等运动状态。

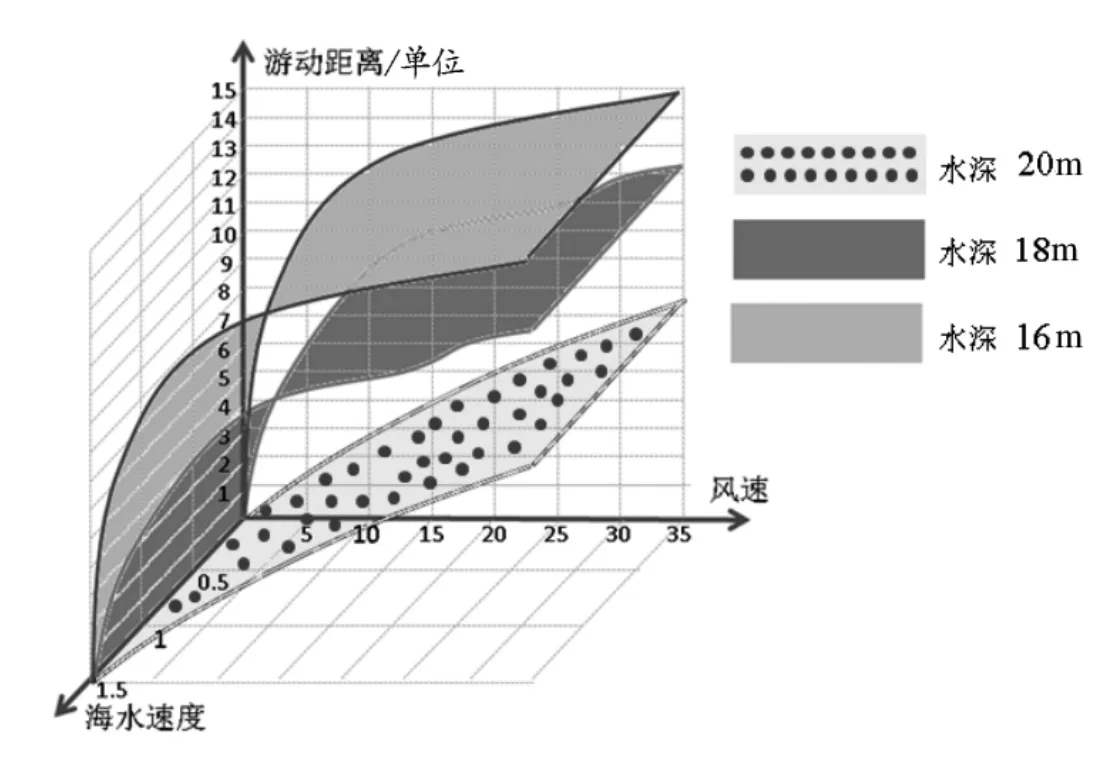
图1 系泊系统游动距离图

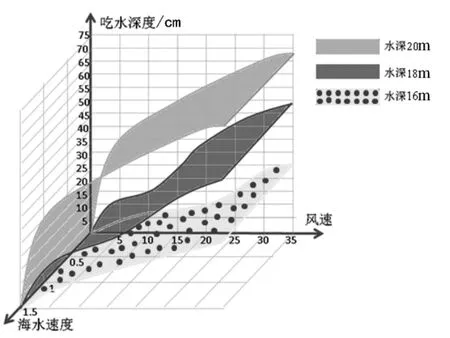
图2 系泊系统吃水深度