小学数学教师图形与几何知识状况调查——以上海市浦东新区为例
2020-10-28尹瑶芳
尹瑶芳
小学数学教师图形与几何知识状况调查——以上海市浦东新区为例
尹瑶芳
(上海市浦东新区教育学院附属学校,上海 201299)
图形与几何是小学数学课程内容的重要组成部分,为了解小学数学教师对图形与几何知识的掌握状况及特点,以浦东新区为例,运用问卷调查和个别访谈对研究问题进行探究,结果显示:知识掌握程度按照从多到少的排序为坐标几何、度量几何、画法几何、演绎几何、直观几何、变换几何和与之相关的文化知识,其中坐标几何、度量几何和画法几何总体掌握较好;变换几何和与之相关的文化知识最为欠缺;直观几何和演绎几何知识掌握较为薄弱,居于中间.年龄、教龄和职称与教师图形与几何知识有显著相关,在某些维度表现上有差异;性别、学历与教师图形与几何知识没有显著相关.研究对提升小学数学教师知识提出了建议.
图形与几何知识;教师知识评价;教师特征变量;小学数学教师
1 问题提出
教师专业化发展思潮促进教师知识的研究,其焦点问题是教师知识的问题,课程改革的实施要求教师拥有适切的知识结构,小学数学教师学科知识缺失的现状急需改变.
众多学者从不同角度强调学科知识在教师知识结构的重要作用.例如,艾尔伯兹(Elbaz F.)[1]的学科“内容知识”;舒尔曼(Shulman)[2]的“学科知识”;林崇德、申继亮、辛涛[3]的“本体性知识”;叶澜[4]的“学科专业知识”等.王桃枝[5]指出,专业学科的理论知识是专业课教师知识结构的特色所在,学术无专攻,就不能成为本专业学科的教师.
一些学者从不同视角开展小学数学教师知识结构的现状调查研究,在新课程改革实施的十多年之中,曹培英[6]、陈慧君[7]、卢锦玲[8]、李渺[9]、李琼[10]等通过调查研究,得出中国小学数学教师本体性知识缺失是存在的,以至于在教学过程中出现诸多问题,不仅影响了数学教学质量的提高,也在一定程度上影响了学生的全面发展.
学者们对教师知识结构的表述虽不一致,但都会把学科知识放在首位,因为学科知识不仅是教师从事某门课教学的基础,同时又是实现教师专业化的一个很重要的因素.所以,研究教师的学科知识是有价值的,有利于丰富教师教育培训理论依据,有助于推进小学数学教学和教育实践.教师学科知识的完善对于促进教师专业化有着不可小视的作用.
为了解小学数学教师对学科知识的掌握状况及特点,了解其知识素养能否胜任新课程改革不断深入的需要,通过阅读文献,了解国内外教师教育的相关理论[11]和研究[12],将其作为研究的理论基础[13].以2011版国家数学课标为依据,从数学学科知识(mathematics knowledge,以下简称MK)的视角出发,对小学数学教师学科知识中的图形与几何知识的掌握现状展开调查分析.以上海市浦东新区为例,通过整群抽样的方法选取样本教师作为研究对象,具体研究的问题是:小学数学教师图形与几何知识掌握现状如何?具体分解为以下小问题:小学数学教师图形与几何知识掌握总体现状如何?在7个维度上表现如何?教师特征变量(性别、年龄、教龄、学历和职称)对图形与几何知识掌握是否存在影响?
2 研究设计
2.1 研究方法
研究采用问卷调查法和个别访谈法,编制测验卷对小学数学教师进行调查,依据访谈提纲进行若干教师的个别访谈,调研在2016学年度第一学期的第6周先是抽部分教师集中进行预测验,批改后对某些题目微调,对测试方式等作适当调整,第7周进行正式卷测试,由学校教导组织教师集中某教室在规定时间内完成;2016学年度第二学期的第8周,请数学学科带头人在课程培训中抽时间请学员独立完成,最后对数据运用SPSS19.0软件进行统计分析.个别访谈依据访谈提纲,运用面谈或微信视频等方式了解教师解题过程的困惑,分析教师知识掌握薄弱原因等.
2.2 工具编制
图形与几何是小学及初中阶段的主要知识点[14].研究重在考查教师掌握知识的状况,测试问卷分为两个部分.第一部分是关于教师的个人背景信息,如性别、年龄、学历、教龄、职称、是否为骨干教师等;第二部分是图形与几何的知识测验题目,从7个方面考查教师知识(如表1所示),包括直观几何、度量几何、变换几何、坐标几何、演绎几何、画法几何、与之相关的文化(表中简称“相关文化”).
研究者参考已有问卷[15],选择并改变了部分题目.第一部分是判断题,共9题,每题3分;第二部分是单项选择题,共8题,每题3分;第三部分是简答题,即开放题,共7题,每题7分.题目考查类别及对应题目如表1所示.
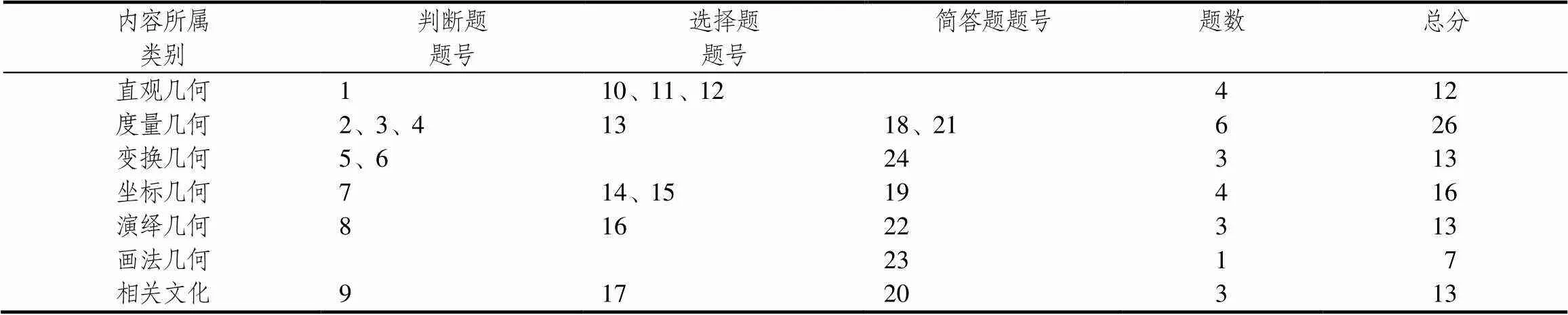
表1 图形与几何测试题的分布
测试卷的信度在可接受范围内,根据SPSS19.0统计分析软件进行数据分析,自编测试题的分半信度为0.812,克隆巴赫系数为0.782,信度较好.测试题是根据《义务教育数学课程标准(2011年版)》《小学数学研究》[16]进行编制的,每道测试题有明确的命题依据及考查目的,请相关专家对测试卷进行了审阅,专家认为测试卷结构和内容效度都是合理的.
测试卷的难度和区分度根据相关计算公式获得.直观几何测验的各项目区分度为0.30~0.54,平均区分度为0.43;画法几何测验的项目区分度为0.37;度量几何、坐标几何和演绎几何测验的各项目区分度在0.20~0.47之间,平均区分度为0.37;变换几何、与之相关的文化测验的各项目区分度在0.25~0.91之间,平均区分度为0.51;从中可以看出具备良好的测试区分度.
测试以基础题的水平为准,结合考虑题目区分度,因受测验时间和题目数量的限制,基础题目所占比例较多,适当考虑中等难度题目和较难题目.从调查结果看,教师在基础题目上的得分率较高,也证实了预先研究设计的判断.
2.3 样本选取
采用分层抽样和整体抽样相结合的方法,分别从上海市浦东新区4个教育署共抽取50所小学,其中地处市区学校20所,地处城镇学校18所,地处乡镇小学12所.从中抽取252位小学数学教师作为研究对象,共发放问卷270份,回收有效问卷252份,问卷回收率为93.3%.其中男教师39人,占比15.5%,女教师213名,占比84.5%.访谈对象从4个年龄段中分别选取2位非骨干教师,从区骨干教师和学科带头人中选取2位,共10位教师.
使用SPSS19.0统计分析软件对252位教师的图形与几何知识成绩进行正态性检验,结果表明,描述统计结果中,偏度系数为0.153,峰度系数为0.306;两个系数都小于1,数据呈近似于正态分布;看总分的标准Q-Q图中,各点近似围绕着直线,说明数据呈近似正态分布,说明选取的样本具有较好的代表性.
2.4 评分标准
开放题评分标准由研究者和两位小学数学专家讨论后得出,例如第20题简答题评分标准如表2所示.
3 数据统计与分析
对问卷调查数据使用SPSS19.0统计软件进行统计处理与分析,先把每份测试卷的原始数据一一输入,然后进行描述性统计与分析、相关分析、差异分析和回归分析.对个别访谈数据进行质性分析,得出的结果佐证和补充测试结果.

表2 第20题简答题评分标准
3.1 图形与几何知识的整体状况
对被试成绩进行分析,采用普遍认同的评价等级划分:90分及以上为“优秀”;80~89分为“良好”;60~79分为“合格”;60分以下为“须努力”.
3.1.1 教师图形与几何知识的成绩描述
统计结果显示(如图1),252名样本教师总成绩处于合格(=60)及以上的为221人,占87.7%,平均分73.1分,中位数76.0分,众数85.0分,标准差13.6分,极差81.0分,说明小学数学教师图形与几何总体成绩较好,但离散程度大.
各分数段人数分布,教师总成绩主要集中在“60~69”“70~79”“80~89”这3个中间分数段,人数分别是54人、77人和71人,占比分别是21.4%、30.6%、28.2%.其中,“90~100”有19人,占比7.5%;而“0~29”“30~39”“40~49”“50~59”分别有2人、4人、12人、13人,分别占比0.8%、1.6%、4.8%、5.2%.
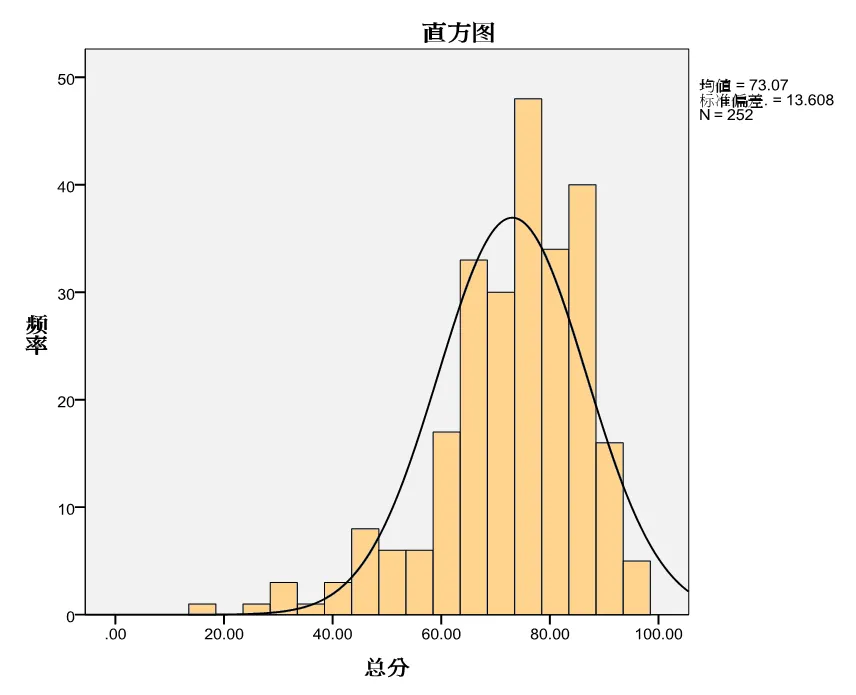
图1 教师图形与几何总成绩分布
3.1.2 教师图形与几何知识掌握水平分布
统计结果显示:达到优秀的有19人,占比7.5%,达到良好的为71人,占比28.2%,这两项总计有35.7%的教师对图形与几何的知识掌握得较好.合格的有131人,占比52.0%,说明大部分教师掌握了基本的图形与几何知识,而须努力的人数有31人,占比12.3%.说明这部分教师图形与几何知识非常欠缺.
进一步对教师图形与几何得分状况分析,结果显示,不同教师的图形与几何知识结构具有不同特点.以得分为82分(良好水平)的4位教师为例,虽然4人的总分相同,但只有教师2在7个维度的得分率稍显均衡,其他3人在各维度的得分率均具有较大的差异.
3.1.3 教师图形与几何各维度的得分状况
通过对图形与几何知识7个维度进行细化分析,从得分情况来看,坐标几何平均得分率最高为84.4%,标准差为2.43;与之相关文化平均得分率最低为49.1%,标准差为3.34,具体如表3所示.
依据得分率来看,7类知识教师得分率从高到低的排序为:坐标几何、度量几何、画法几何、演绎几何、直观几何、变换几何、与之相关的文化的知识.其中掌握最好的坐标几何知识,最差的是与之相关的文化知识.标准差最大为4.52是度量几何,表明教师得分与均值之间差异较大;画法几何标准差最小为2.70,说明教师得分与均值之间差异较小.
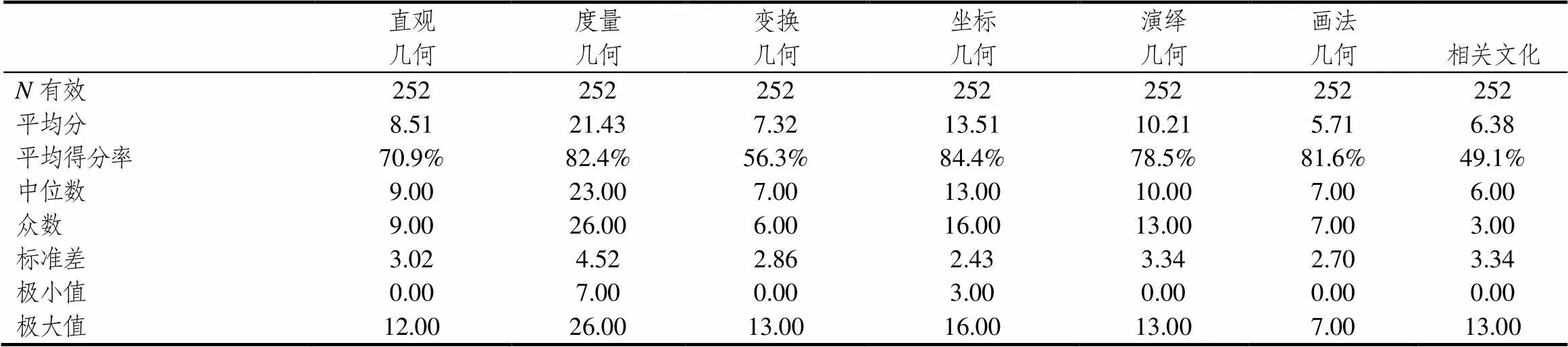
表3 教师图形与几何知识各维度的得分状况
使用SPSS19.0统计软件对图形与几何7个维度的分值进行Pearson相关性分析,结果显示,如直观几何与度量几何、变换几何、坐标几何、演绎几何、画法几何、与之相关的文化之间的相关系数分别为0.237、0.322、0.124、0.322、0.273、0.365,除了直观几何与坐标几何之间的相关系数在0.05水平(双侧)上呈现出显著相关,其它全部在0.01水平(双侧)上显著相关.
从各维度的掌握水平划分,达到优秀和良好的教师其知识掌握较好.而合格只能说是教师掌握知识的下限,但还是有许多欠缺之处,需要加以学习和提升.
如表4所示,百分比表示在相关维度中达到相应等级的样本教师的数量与总量的比,从中能一目了然看出教师各维度图形与几何知识掌握状况.
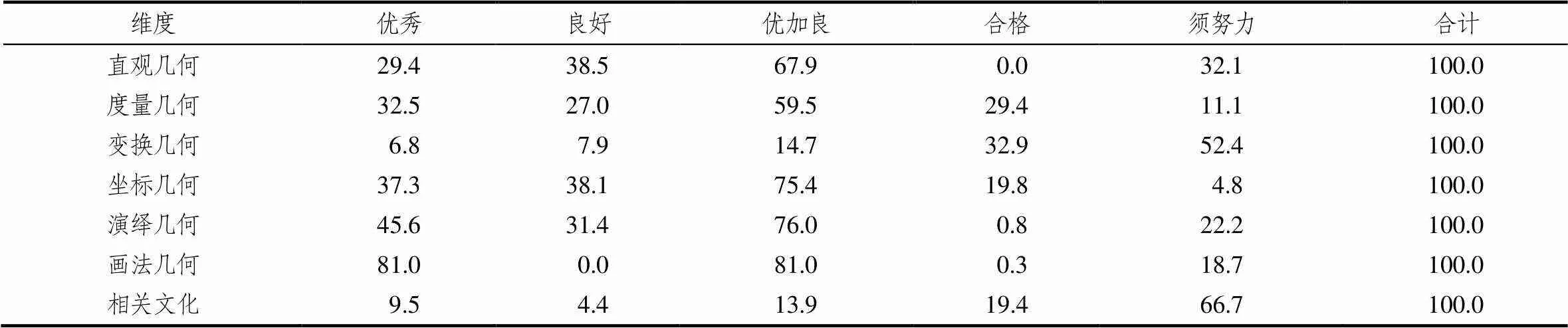
表4 教师图形与几何知识各维度掌握状况
从优秀加良好的等级占比来看,从高到低排列:画法几何、演绎几何、坐标几何、直观几何、度量几何,这些维度教师掌握较好.而较欠缺的变换几何和与之相关的文化,占比不到15%,与之对应的须努力分别为52.4%和66.7%.
从中发现,样本教师在直观几何等7个维度的知识掌握状况,坐标几何、度量几何和画法几何总体掌握比较理想,做得较好;演绎几何和直观几何相对掌握得较差些;而变换几何、与之相关的文化的知识掌握得最不理想,欠缺较多,需要重点加以学习与提升.
3.2 各类特征变量对教师知识的影响分析
3.2.1 各类特征变量与教师总成绩的相关分析
对不同特征变量与教师总成绩进行相关分析,结果表明,年龄、教龄与教师总成绩在0.01水平(双侧)上显著相关,职称与教师总成绩在0.05水平(双侧)上显著相关,而性别、学历与之没有显著相关.
3.2.2 各类特征变量与教师总成绩的回归分析
上述年龄、教龄和职称与教师总成绩存在显著相关,把年龄、教龄和职称分别作为自变量,把总分作为因变量,进行一元回归分析,结果统计如表5所示.变异量显著性检验值小于0.05,说明回归模型整体解释变异量达到显著水平.结果显示,年龄、教龄、职称对教师图形与几何知识均有显著影响.以上3个变量对教师图形与几何知识影响的解释程度为3.3%.
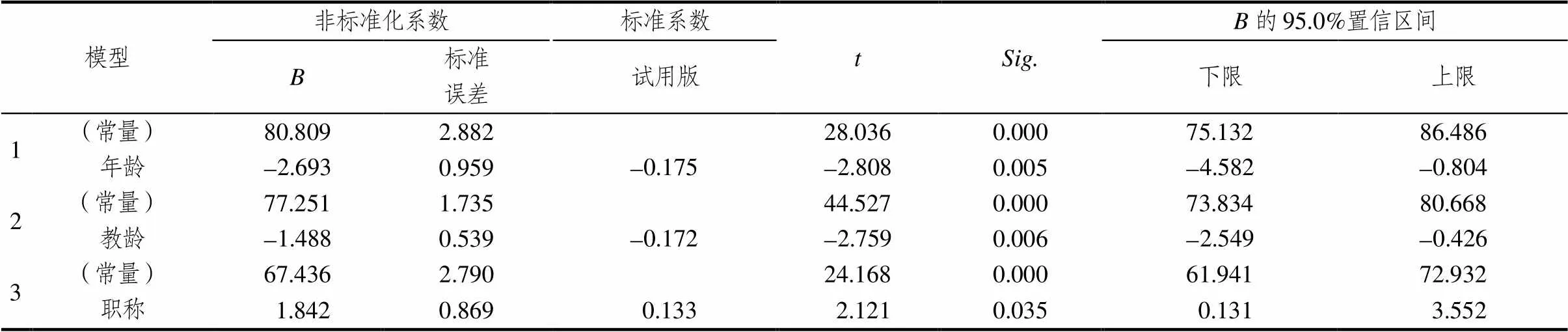
表5 3个教师特征变量与教师总成绩的回归模型系数
注:因变量:总分
3.3 不同个人特征教师图形与几何知识的差异分析
为了进一步考查不同的教师背景变量对教师知识的影响,下面分别对性别、年龄、教龄、职称、学历不同的教师在图形与几何知识上的差异进行分析[17].
3.3.1 男女教师图形与几何知识差异分析
参与问卷调查的男教师有39人,女教师有213人.统计结果显示,从得分总分来看,男教师的总均值(=69.64)略低于女教师(=73.69),男教师的标准差(=14.09)略高于女教师(=13.45),说明男教师的总体表现劣于女教师,个体差异则大于女教师.对男女教师图形与几何知识成绩进行独立样本检验,结果显示,男女教师的总成绩及7个维度得分之间都没有显著差异.具体见表6所示.
综上可知,男教师的总体表现劣于女教师,具体到7个维度,男教师只有在直观几何维度上优于女教师,其它6个维度均低于女教师.从总成绩和7个维度的成绩来看,男女教师之间均无显著差异.
3.3.2 不同年龄组和教龄组教师知识得分的分析
教师按年龄段分为4组:20~30岁为第1组,31~40岁为第2组,41~50岁为第3组,51~60岁为第4组.从年龄组的平均分来看,从高到低依次排列为第1组均值(=75.45)>第2组均值(=72.40)>第3组均值(=70.68)>第4组均值(=65.12),后面3组教师平均分都低于总体平均分(=73.1),说明随着年龄的增长,教师的得分表现越来越差.从7个维度的状况来看,除了度量几何从高到低依次为第3组>第2组>第1组>第4组外,其余6个维度得分从高到低依次均为第1组>第2组>第3组>第4组,即随着年龄增长呈现下降趋势,具体如图2所示.
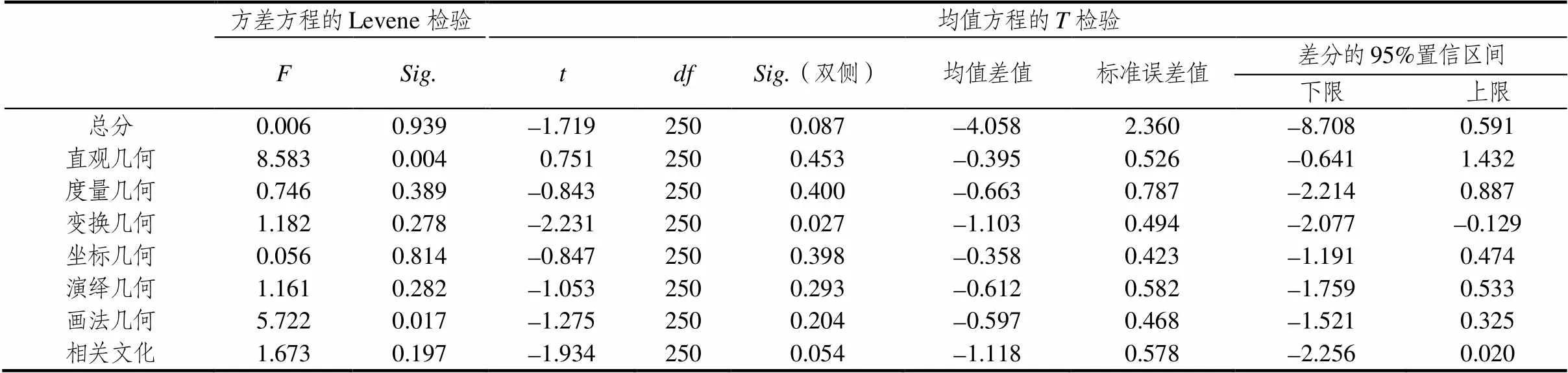
表6 男女教师图形与几何成绩差异分析
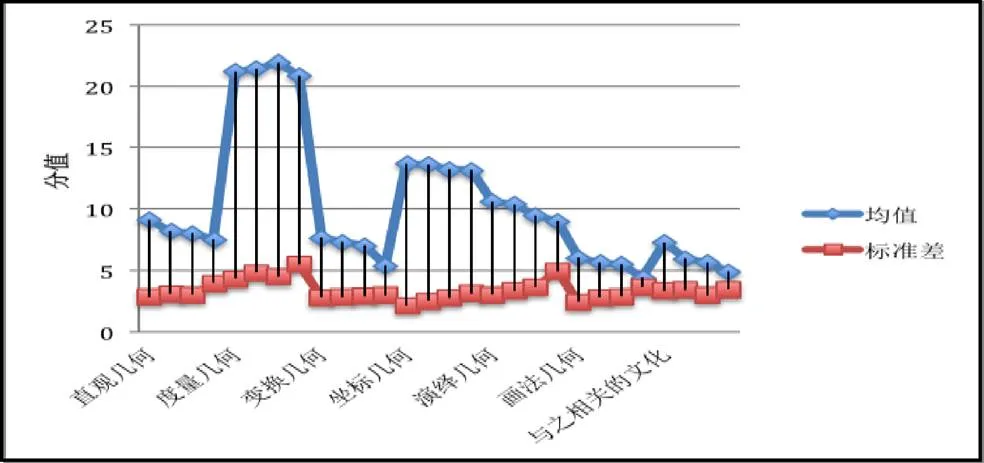
图2 不同年龄组教师7个维度均值状况
基于差异,研究采用多变量方差分析对4个年龄组教师的7类知识均值进行比较分析.结果发现,直观几何(=2.744,=0.029)、度量几何(=1.775,=0.029)、坐标几何(=1.911,=0.039)中<0.05,表明4个年龄组别有显著的差异;与之相关的文化(=2.848,=0.001),值小于0.01,4个年龄组别有显著的差异;变换几何、演绎几何和画法几何维度差异不显著,而每个组内各个维度均无显著的差异.
从教龄组总的平均分来看,从高到低依次排列为第1组(4年及以下)均值(=75.61)>第2组(5~10年)均值(=74.60)>第4组(16~20年)均值(=72.75)>第3组(11~15年)均值(=71.37)>第5组(21年及以上)均值(=69.25),后面3组教师平均分都低于总体平均分(=73.1),说明教师教龄最长的第5组,得分表现却最差.
经方差分析,不同教龄教师在直观几何、演绎几何、与之相关的文化3个维度有显著差异,其它4个维度没有显著差异.具体来讲,不同教龄的教师在直观几何知识(=3.143,=0.015)、演绎几何知识(=3.130,=0.015)及与之相关的文化知识(=4.347,=0.002)上有非常显著的差异.经过对5个教龄组得分的多重比较,检验均值差的显著性水平为0.05,发现有4个维度中的一些组别有显著差异.
直观几何:发现第1组分别与第3组、第5组有显著差异,第2组分别与第3组、第5组有显著差异;变换几何:发现第1组与第5组有显著差异;演绎几何:发现第1组与第5组有显著差异,第4组与第5组有显著差异;与之相关的文化:发现第1组分别与第3组、第4组、第5组有显著差异;第2组与第5组有显著差异.
3.3.3 不同职称组教师7个维度的方差分析
职称按以下分组:小高及以上为第1组,小学一级为第2组,小学二级为第3组,未评职称为第4组.其总分的平均分来看,从低到高依次排列为第1组总均值(=70.09)<第2组总均值(=74.47)<第3组总均值(=74.71)<第4组总均值(=75.13),后面3组教师平均分都高于总体平均分(=73.1),显示随着教师职称依次升高,教师知识掌握反而依次降低.
从7个维度状况来看,直观几何、度量几何和画法几何3个维度小学一级教师做得最好;变换几何和与之相关的文化2个维度,未评组教师做得最好;坐标几何和演绎几何小学二级教师做得最好;直观几何、变换几何、画法几何和与之相关文化,小高及以上教师做得最差,具体见图3所示.
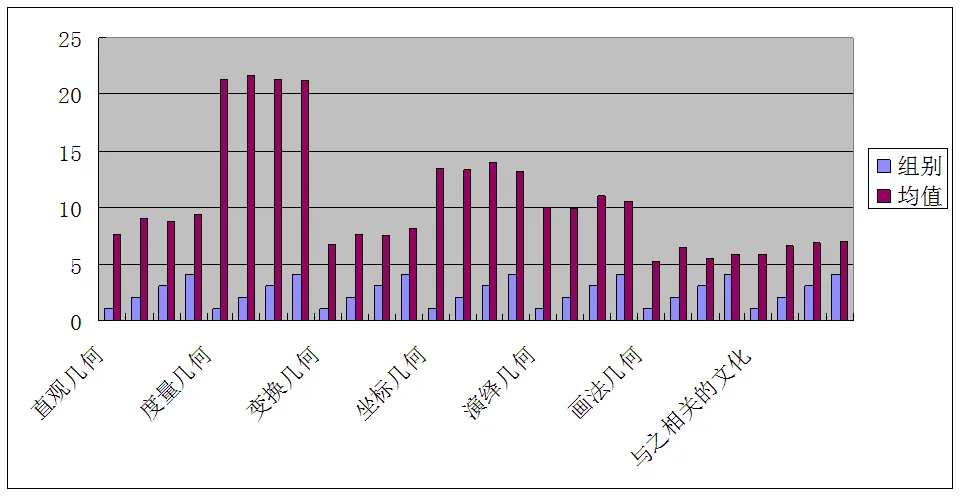
图3 不同职称组教师7个维度均值状况
不同职称教师在直观几何和与之相关的文化2个维度有显著差异,其它5个维度没有显著差异.具体来讲,不同职称的教师在直观几何知识(=3.150,=0.015)、与之相关的文化知识(=2.592,=0.003)上有显著的差异.
3.3.4 不同学历组教师7个维度的方差分析
统计结果发现,教师的知识掌握总成绩基本与学历水平成正比关系,第1组为大专及以下学历、第2组为本科及以上学历的教师,后者的总分均值高于前者.各维度除了演绎几何外,其它维度均是第2组教师大于第1组教师.对两组教师的图形与几何知识总成绩及各维度成绩进行检验,结果表明两组教师没有显著差异.
3.4 访谈质性分析
从教师访谈情况发现,26~30岁的青年教师都拥有全日制本科文凭,都经过高中学习,接受大学高等数学学习等,数学知识功底相对较为扎实;40岁以上的教师职前接受的是中等师范教育,然后通过在职进修学习达到大专或本科水平,当时开设理科的不多,所以大都就读中文或教育学或管理等专业,数学专业知识补充相对较少.
在职继续教育培训课程,选修关于提升图形与几何知识的课程比较稀少;即使有数学方面的课程,也大都渗透在其它培训课程中,能选修到专门培训的教师不多;大部分教师接受这样的培训机会较少,一般靠教师利用业余时间自学获得,虽能提升但学习不够系统、全面.部分教师没能跟上图形与几何课程设计变化,如2001年版和2011年版的数学课标增大了直观几何和变换几何的比重.以往教师对这部分接触不多,相对陌生,只是依靠在教学实践中慢慢积累.
部分教师受教育观和知识观的限制,对任教年级的教科书研读不够,理解不深.中老年教师由于长期任教小学数学,不可避免出现几何知识的遗忘,再加上学习前沿知识不够主动积极,出现数学思维“童化”的现象.教师对新课程的准备性知识和对新增内容认识的宽度和广度等[19]有些不足.
4 结论与建议
4.1 结论
(1)从测试调查总体来看,样本教师知识掌握程度按照从多到少的排序为:坐标几何、度量几何、画法几何、演绎几何、直观几何、变换几何和与之相关的文化知识.252名样本教师总成绩说明小学数学教师图形与几何总体成绩较好,但离散程度大.等级统计结果显示:达到优良的35.7%的教师对图形与几何的知识掌握较好;合格的52.0%的教师掌握了基本知识,须努力的12.3%的教师知识非常欠缺.
(2)从具体维度测试来看,呈现以下特点.
变换几何、与之相关的文化知识最为欠缺.变换几何需要教师弄清变换几何的本质,平移、旋转和轴对称的概念,能够从变换几何的视角分析和设计相关的图形,教师理解和鉴赏能力的提升有利于帮助学生掌握相关的知识.与之相关的文化考查的第五公设是欧氏、罗氏和黎曼几何的本质区别一题,教师普遍对之非常陌生.同样考查的分形几何的特点和性质的知识,教师也是非常欠缺,说明教师视野不够开阔,对前沿知识不够了解.小学教师要具备深厚和广阔的文化底蕴,才能组织学生进行分形图形等规律探究和图形的欣赏.
直观几何和演绎几何知识掌握得较为薄弱.直观几何方面,考查的认识三视图、认识维度知识、实践操作等,教师掌握得不够好,如选择题第11题正确答案应该是椭圆形,但许多教师认为这条曲线是圆形,可能受限于小学中圆的认识的操作过程.演绎几何方面,考查的三角形内角和是180度,部分教师失分主要是证明理由遗漏或书写不完整.
坐标几何、度量几何和画法几何总体掌握较好.坐标几何知识,教师普遍掌握较好;度量几何方面,考查的弧度制的精髓教师判断错误较多,而简答题18教师扣分原因主要是表述不够完整,长方形面积公式推导,教师一般知道公式推导的过程,但书写过于简单,阐述不够完整且明确.有18.7%的样本教师须努力,不理解标准的斜二侧画法的意义和画法.有81.0%的教师能够画得非常正确,用二维图形正确表达三维立体图形.
(3)从个人特征变量回归分析看.年龄、教龄和职称与教师图形与几何知识有显著相关;性别、学历与教师图形与几何知识无显著相关;不同年龄、教龄和职称教师在某些维度表现上有差异.
(4)访谈结果显示,教师数学专业知识相对不足.中老年教师在职提升本专科学历时就读理科不多;在职培训选修几何课程较少;受教育观和知识观的限制,出现数学思维稚化现象[15];对新课标增加几何内容宽广度认识不足[18]等.
4.2 建议
基于上述测试与访谈的结论,提出如下建议.
(1)针对图形与几何知识,开发实施培训课程.
已有文献以案例研究为视角,认为数学学科教学知识(MPCK)在教师培训中发挥独特的作用[19],相关研究如徐章韬[20]、钱旭升[21]等给大家以启迪.教师培训者可以搜集一些带有普遍性问题的“图形与几何”方面的教学案例,特别是针对教师欠缺的知识模块,对课程内容的数学基础与核心内容分析,开发相关的专项培训课程,把薄弱点作为培训重点,并扩大一些前沿相关图形与几何知识,如分形几何等,培训更具针对性和有效性[22].
(2)使用现代教育技术,扩大课程受训教师群体.
运用CCtalk实施互动教育平台,该平台为能上课的网师提供完善的在线教育工具和平台能力,为学员提供一起学习的社群环境.运用该平台,可以把需要培训的教师建立学习群,约定时间有专家进行直播主讲,该平台具有互动性强、界面舒服、功能齐全等特色,教师使用移动终端可以学习,错过直播也不用愁,支持观看视频回顾,随时随地碎片化学习,和其他学员交流心得、讨论观点等.基于调研,开发分层培训课程等,供全国各地有需求的教师网上选修学习.
(3)运用学科工作坊等方式,适当增加培训内容.
在多项关于教师知识来源的调查中,教师认为教学参考书是极为重要的来源之一[23].一般教师都重视数学参考书的使用,但考虑到改编参考书存在时间周期长,即时效果不理想的情况,可以利用学科工作坊等方式,适当增加与拓展图形与几何相关内容,针对性地指导相关内容,如对知识点的本质是什么,如何理解,怎样正确解答,在教学中应注意什么等翔实指导[24].以方便教师认识与理解图形与几何教学内容的深度和广度.
(4)加强正确知识观宣传,不断提升教师素养.
提高教师教学水平的核心是提升教师的MPCK,而其中数学学科知识(MK)是一个重要方面[25].教师如果具有比较宽广的面向教学的数学知识,理解知识来源和纵横联系,才能够进一步帮助学生[26-27].所以要大力加强正确知识观的宣传,促使教师拥有这方面意识,加强学习和深刻理解数学的本质,自学加以弥补或是争取机会外出学习,与时俱进地提升自己的数学素养,能游刃有余地帮助学生学好数学,做好小升初的无痕衔接等.
5 反思与展望
研究限于个人的时间与精力,仅采用整群随机抽样的方法获得样本,样本对象为浦东新区小学数学教师,调查问卷仅选择每一维度的典型题目,仅是一次性调查,研究结论具有适用性局限,推广应用务必谨慎.研究对浦东新区小学数学教师图形与几何知识掌握现状进行了定量研究,结合对原因进行质性分析,得出结论,给本地教师继续教育培训及课程开发提供实证依据.今后也可进一步扩大研究范围、增加研究内容和丰富考查题目形式等,以便深入挖掘教师几何知识掌握的欠缺之处,还可进行学校或跨地区比较研究等.
致谢:特别感谢华东师范大学孔企平教授的热情指导.
[1] 石生莉.教师实践知识研究[J],教育理论与实践,2005,25(5):24-27.
[2] SHULMAN L S. Paradigms and research programs in the study of teaching: A contemporary perspective [M] // WITTROCK M C. Handbook of research on teaching. 3rd ed. New York: Macmillan, 1996: 3-36.
[3] 林崇德,申继亮,辛涛.从教师的知识结构看师范教育的改革[J].高等师范教育研究,1999(6):12-17.
[4] 叶澜.新世纪教师专业素养初探[J].教育研究与实验,1998(1):41-46.
[5] 王桃枝.如何完善专业课教师的知识结构[J].职教通讯,1998(8):12-13.
[6] 曹培英.新课程背景下小学数学教师本体性知识的缺失及其对策研究[J].课程·教材·教法,2006,26(6):40-45.
[7] 陈慧君.小学数学教师知识结构的调查研究[D].长春:东北师范大学,2007:1-40.
[8] 卢锦玲.沪港两地小学数学教师专业知识缺失的比较研究[D].上海:华东师范大学,2008:1-229.
[9] 李渺,喻平,唐剑岚,等.中小学数学教师知识调查研究[J].数学教育学报,2007,16(4):31-34.
[10] 李琼,倪玉菁,萧宁波.小学数学教师的学科知识:专家与非专家教师的对比分析[J].教育学报,2005,1(6):57-64.
[11] SHULMAN L S. Those who understand: Knowledge growth in teaching [J]. Educational Researcher, 1986, 15 (2): 4-14.
[12] 柳笛.美国数学教师学科内容知识的研究述评[J].数学教育学报,2010,19(6):74-78.
[13] 李琼,倪玉菁.教师知识研究的国际动向:以数学学科为例[J].外国中小学教育,2006(9):6-11.
[14] 吴正宪,韩玉娟.图形与几何内容的理解与把握——《义务教育数学课程标准(2011版)》解析之七[J].小学数学教育,2012(Z2):24-26.
[15] 刘帅.小学数学教师几何知识掌握状况的调查研究——以吉林省小学数学骨干教师为例[D].长春:东北师范大学,2012:50-51,58-64.
[16] 张奠宙,孔凡哲,黄建弘,等.小学数学研究[M].北京:高等教育出版社,2009:122-123.
[17] 韩继伟,黄毅英,马云鹏,等.初中教师的教师知识研究:基于东北省会城市数学教师的调查[J].教育研究,2011,32(4):91-95.
[18] 宁连华.新课程背景下高中数学教师教学知识的调查研究[J].教育理论与实践,2008,28(10):14-16.
[19] 胡典顺,徐汉文,李倩.实习教师与专家教师教学特质比较——以“圆的方程”为例[J].数学教育学报,2009,18(3):70-73.
[20] 徐章韬,龚建荣.学科知识和学科教学知识在课堂教学中的有机融合[J].教育学报,2007,3(6):34-39.
[21] 钱旭升,童莉.数学知识向数学教学知识转化的个案研究——基于新手与专家教师的差异比较[J].长春理工大学学报(高教版),2009,4(3):155-157.
[22] 廖冬发,周鸿,陈素苹.关于中小学教师学科教学知识来源的调查与分析[J].教育探索,2009(12):90-92.
[23] 尹瑶芳,孔企平.国内中小学教师MPCK来源研究的定性元分析[J].数学教育学报,2016,25(5):22-27.
[24] 鲍建生.几何的教育价值与课程目标体系[J].教育研究,2000,21(4):53-58.
[25] 吴卫东,彭文波,郑丹丹,等.小学教师教学知识现状及其影响因素的调查研究[J].教师教育研究,2005,17(7):59-64.
[26] 徐章韬,顾泠沅.师范生课程与内容的知识之调查研究[J].数学教育学报,2014,23(2):1-5.
[27] 徐章韬,顾泠沅.面向教学的数学知识之调查研究[J].全球教育展望,2014,43(4):93-101.
Investigating Mathematics Teachers’ Knowledge of Figures and Geometry in Elementary School
YIN Yao-fang
(School Affiliate of Shanghai Pudong New Area Education College, Shanghai 201299, China)
Figures and geometry are important parts of elementary school mathematics.This study mainly used questionnaires and interviews to investigate teachers’ knowledge about these two learning areas. We found that, first, students’ mastery of knowledge can be ranked in descending order as: coordinate geometry, measurement geometry, descriptive geometry, deductive geometry, intuitive geometry, transformation geometry, andthe culture related to geometry. Second, teachers’ age, teaching age, and professional title have a significant correlation with their knowledge of the learning area of figures and geometry. Their gender and educational background do not affect their knowledge of geometry. We also provide some suggestions for improving teachers’ knowledge about graphics and geometry.
knowledge of figures and geometry; evaluation of teachers’ knowledge; teacher’s characteristic; primary school mathematics teacher
G635.5
A
1004–9894(2020)05–0046–06
尹瑶芳.小学数学教师图形与几何知识状况调查——以上海市浦东新区为例[J].数学教育学报,2020,29(5):46-51.
2020–04–09
2014年浦东新区区级课题——小学数学教师几何知识缺失的调查研究(2014规划49)
尹瑶芳(1964—),女,上海人,博士,中学高级教师,主要从事学校课程与教学、数学学科教育教学和数学教师教育研究.
[责任编校:张楠、陈汉君]
