小学生数学符号意识分析框架的构建
2020-10-28陶红强
陶红强
小学生数学符号意识分析框架的构建
陶红强
(溧阳市汤桥小学,江苏 常州 213300)
符号意识作为学生的核心素养,理应受到重视.构建一个能从具体行为层面来分析小学生数学符号意识的框架,是发展学生符号意识的重中之重.基于国内外有关符号意识操作性定义的分析,结合相关理论与实践,构建了一个关于小学生数学符号意识3个维度(符号认识、符号理解、符号运用),15个具体成分的分析框架.
小学段;符号意识;分析框架;维度
数学符号意识作为小学生的一个重要核心素养[1],理应受到数学教育的重视.目前,国内外关于符号意识的研究主要集中在其内涵的界定、要素的构成和策略的培养3个方面.而作为一线教师,最为困惑的是不能从操作层面来有效培养学生的符号意识.究其原因,符号意识的内隐性导致广大一线教师不能有效地将抽象的符号意识概念具体化到行为层面,继而不具有可操作性.因此,构建一个能分析小学生数学符号意识发展水平的分析框架,即构建一个数学符号意识的行为评估指标,是非常必要而又紧迫的.研究者尝试在符号意识内涵(主要从符号意识的操作性定义)的分析基础上,对小学阶段有关数学符号内容及其符号意识的表现形式进行梳理,并结合相关理论对教学实践中学生表现出的符号意识做出分析,最终构建出小学生数学符号意识的分析框架.
1 对数学符号意识内涵的认识
关于符号意识内涵的界定,国内外学者已经做了大量有价值的探讨,虽然在认识上还不统一,但主要集中在3个视角:“数学学科、符号学和心理学.”[1]
1.1 数学学科视角下的符号意识
“数学的本质是概念和符号,并通过概念进行运算和推理.”[2]从数学本质这一视角出发,符号意识的内涵主要表现在数学抽象、数学理解和数学应用方面.例如,《义务教育数学课程标准(2011年版)》对符号意识的内涵界定为“符号意识主要是指能够理解并且运用符号表示数、数量关系和变化规律;知道使用符号可以进行运算和推理,得到的结论具有一般性.建立符号意识有助于学生理解符号的使用是数学表达和数学思考的重要形式”[3].数、数量关系、规律都是数学抽象的产物,用数学符号表示这些抽象的数学对象,既是发展符号意识的重要途径又是分析学生符号意识的重要途径.同样,对符号意识有可操作性定义的观点有:“符号意识内涵包括理解并会用符号表示数、数量关系和变化规律;用符号进行运算和推理.”[4]“能够理解并运用符号去表示数学的意义和结构、运用符号进行运算和思考.”[5]“符号意识的要求具体体现在符号理解、符号操作、符号表达和符号思考4个维度.”[6]可见,虽然上述关于符号意识的具体表述不同,但都是从数学学科视角出发的,且都是针对符号意识的行为层面来讲的,具有操作性.
1.2 符号学视角下的符号意识
黄玉顺教授认为“西方符号学有3大系统,即索绪尔开创的语言学系统、皮尔士的分析哲学系统与胡塞尔的现象学符号系统”[7].语言学研究的是符号系统,其关注的是“符号承载知识和信息的功能”[7].例如,索绪尔指出符号概念:“当事物A可以作为事物B的替代而代表事物B时,事物A就是事物B的符号.”[1]同时指出,一个符号由“能指”和“所指”组成.符号学研究的是符号本体,“探讨的是符号的本质,强调的是符号自身的特性”[7].例如,皮尔士指出:“符号包含符号、对象和解释3个主题,对象可以是现实事物或另一个再现符号,而符号在与对象的联系中,在符号使用者的头脑中便产生了解释.”[8]同样也比较注重解释的是胡塞尔的现象学,其研究的符号强调的是对符号文本意义的解释.
以上符号学的3大系统虽然代表3种不同的视角,但都强调了符号的功能性和符号理解的重要性.这可以提示研究者可从符号的功能方面和学生对符号的理解水平方面来设计具体行为指标,进而分析学生的符号意识.
1.3 心理学视角下的符号意识
从心理学的视角界定符号意识,主要是从意识出发进行相关定义.意识是“包括感知觉在内的一种最高级的认识活动,思维在其中起着决定性的作用,具有自觉性、能动性、创造性等特点”[8].可见,符号意识要注重人的能动性,从操作性层面来讲主要体现在对数学符号的表达与理解的主动性.郑毓信教授认为:“会进行符号间的转换与能选择适当的秩序和方法解决用符号所表达的问题而言,主要地都应看成一种自觉的努力.”[9]其所指的“自觉的努力”就是一种主动性的体现.
基于对以上数学符号意识的三维视角(数学学科、符号学、心理学)的分析,研究者认为小学生数学符号意识的分析框架的构建应具备以下几个标准:第一,要关注学生的主观能动性,因为符号意识强调人的一种感悟;第二,注重数学的功能性特征,既包括符号的内在功能性又包括符号的外在功能性.本着这一指导方向,对6个年级的数学符号内容进行梳理,并对符号意识的表现形式做了具体的分析.
1.4 小学段数学符号类型及其符号意识的具体表现
邵光华教授根据符号的意义把数学符号分为6大类:“元素符号、运算符号、关系符号、结合符号、约定符号、简练表达式或缩记符号.”[10]以此为依据,并根据《义务教育数学课程标准(2011年版)》的要求、对数学教科书(苏教版)数学符号内容进行梳理分析,总结得出小学段数学符号类型及其符号意识的具体表现.限于篇幅,仅以元素符号为例(见表1).

表1 小学数学元素符号及其符号意识的表现形式
由表1可以看出,随着数学学习的展开,以及随着年级的升高,《义务教育数学课程标准(2011年版)》和教科书对学生符号意识的要求也在逐步提高,具体反映在学生对数学符号理解的深度、广度变化,以及学生在表达客观事物数学关系时使用符号表达的意识、频率、合理性、复杂性等方面的差异.例如,元素符号从对整数的会读写到分数、小数的意义理解再到字母的表示与运用;而对字母符号的理解又从某数的替代提升到变量的理解.这些方面为接下来的研究有着两方面的启示:第一,在设计可观察、可测量的符号意识行为指标时,要有发展梯度,即设计不同年度梯度的分析指标;第二,以此为依据进一步指导在教学实践中对学生表现出的不同符号意识进行调查分析.
2 教学实践中数学符号意识的具体表现及分析
2.1 关于符号理解
(1)关于字母、式子的理解.
在课题组老师执教的“运算律”这节课中,有这样一个环节:出示式子“30×12-15×6”,然后让学生给其编题,从符号意识的角度看,这是考察学生的符号理解水平,然而在学生的回答中错误率是很高的,也就说明学生对于理解式子在现实情境中的意义是存在差异的.受此启发,在考察学生的符号意识中应有这样一个成分,即“理解式子在现实情境中的意义”.
在六年级“解决问题的策略——替换”例题教学中,有的学生用方程做,老师在分析学生写的解设“小杯容量ml,则大杯容量为3ml”时,提出这样一个问题:小杯容量中的与大杯容量3中的所代表的意义一样吗?对于此问题,研究者在听课时留意了一下,只有很少学生举手,而且第一个回答的学生回答的是“不一样”.由此可见,理解同一字母在同一情境中的意义也是符号意识的重要成分,并由此想到同一字母在不同情境中的意义也是符号意识的重要成分.例如,对于公式=×÷2与公式=×,这两个公式中的代表的意义一样吗?只有学生理解了其字母所代表的具体意义,才能更好地理解其式子的意义.可见,使学生懂得符号的意义既是学校数学教育的目的之一,又是发展学生符号意识的一个重要途径[11].
(2)理解图像、表格、符号之间的转换.
对于同样的数学对象,不同的学生在解决问题时所表现出的符号意识水平也是有差异的,如图1~图3所示.

图1 学生符号意识水平(一)

图2 学生符号意识水平(二)

图3 学生符号意识水平(三)
从图1到图3所反映的学生水平是有层次的,是典型的由图像表达到符号表达,特别是图2更是清晰地表达了图像与符号之间的层次关系.为发现学生对该题解答的两种水平是否有显著差异,随后以该题为研究材料,选取二年级、三年级、五年级总共141位同学参与调查,利用SPSS处理数据,进行两独立样本检验(结果见表2).表2结果显示=0.000,即图像表达和符号表达的两种水平存在显著差异.由此看来符号表达是最抽象的,是以语言表达、图像表达为基础的.关于这一点,也可以从以下统计的数据得到较好的说明.

表2 两种水平独立样本t检验
针对表3的题目选取五年级3个班100位同学进行了调查(统计结果见表4).根据表4,可以发现:在能正确找到规律的同学中,用文字叙述的要远高于用具体式子表示的和用字母符号表示的.可见,数学符号意识的形成要经历“语言—表象—符号”这一数学学习心理过程.这一数学学习心理过程,与英国数学教育家利贝克的4个基本环节是基本吻合的.利贝克“认为学生的数学学习可以概括为经验、语言、图像和符号4个基本环节,这4个环节可以构成学生学习数学的基本过程”[12].以上教学实践有两点启示:第一,符号意识发展是具有不同层次的,即学生的符号理解是具有层次性的;第二,符号意识是关于学生的语言(文字)、图像、表格、符号的一个体系的构成,分析学生的符号意识要注重学生在自然语言即利贝克所说的经验与图像、表格、符号之间的转换.正如Arcavi所认为的“符号意识应体现在具有从信息(语言和图表)中建构符号关系的意识,并能建构符号关系”[13].

表3 解决问题(从表格中发现什么规律)

表4 几种描述水平情况统计
2.2 关于符号表示
图4是五年级学生在学了“因数和倍数”后所做的作业,学生在没有任何要求和提示下主动将省略号改写成字母概括的方式.这表明学生是有着符号表示的意识的,也就是说,学生有符号表示的主动性的.但对两个班,总计77人,主动这样写的学生总共有4人,成功率仅为5%.也就是说学生的主动性即意识在整体层面是相当低的,这也启发研究者在制定小学生数学符号意识分析标准时,应将“符号表示的意识、正确性、多样性”作为重要的分析指标.
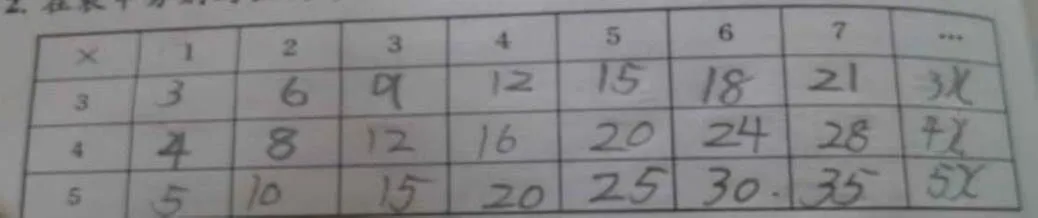
图4 “因数和倍数”课后作业
2.3 关于符号思考
Zorn认为符号意识是“从符号中抽象出涵义和结构,有效地用符号去表达数学意义和结构,以及操作符号发现新的数学涵义和结构的能力”[14].关于这一点,可以从图5~图8很好地得出.

图5 水平1

图6 水平2

图7 水平3

图8 水平4
从图5~图8显然是存在水平差异的.为更好地说明差异情况,研究者以此题作为研究材料,选取三年级、五年级、六年级总共207人作为研究对象,做了描述性统计分析(结果见表5).结果显示:67.3%的人能达到水平1的层次、只有9.6%的人能表示3的所有乘方情况、有20.7%的人能发现3以外数字的乘方、仅有1.9%的人能用符号形式化地表示,可见各个水平之间的差异还是很大的.具体来说,图5、图6所表明学生只能从已有的符号表达中抽象出了涵义和结构,同时也比较有效地运用数学符号去表达了这种意义和结构,但是还未发现新的意义和结构.显然从图7和图8看出,学生已经由3的乘方想到其它如4、5、6等不同数字的乘方,这显然是一种新的发现,表明学生是有着符号思考的意识与能力的,是可以根据已有的符号表达来发现新的数学意义和结构.但同样是新的发现,也显现出不同的水平,如图7仍旧停留在具体的数字对象上,而图8则抽象出字母符号,已经脱离具体对象.从思维程度讲,图5、图6、图7所处在同一思维水平,即皮亚杰所称的具体运算阶段;而图8所反映的思维水平则达到了形式运算阶段.可见,符号思考作也应作为符号意识的一个重要分析指标.
3 小学生数学符号意识分析框架的构建
通过上述对符号意识内涵的界定,对国内外已有研究成果的借鉴,对小学生数学符号内容的梳理,并结合课程标准及教学实践的分析,构建了包含3个维度、15个具体成分的分析框架,见表6.
3.1 符号的认识(维度一)
符号认识作为符号意识的重要维度,是发现和培养学生符号意识的基础.具有数学学科特质的数学符号是与生活符号有着本质的区别的,同样作为数学符号内部系统来讲,根据其不同的意义又可将数学符号进行分类.所以能准确区分数学符号和生活符号以及能正确区分同类数学符号是符号认识的基本要求.这与外国学者Fey所认为的“符号意识应包括认识和鉴别能力”[15]是一致的.
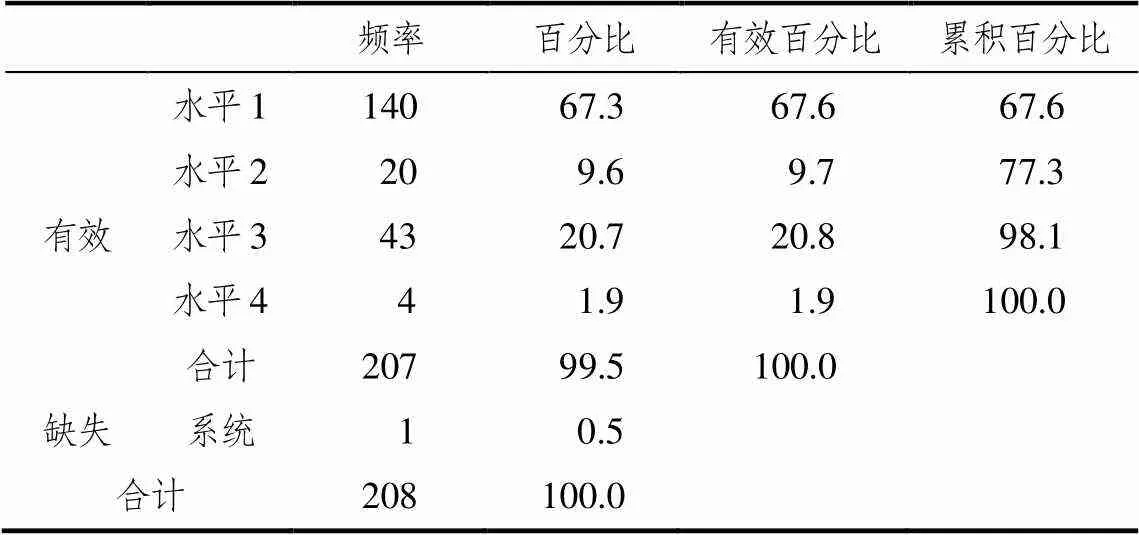
表5 不同水平情况统计

表6 小学生数学符号意识的分析框架
3.2 符号的理解(维度二)
符号理解是发展学生符号意识的关键.“符号理解就是获得数学符号意义的过程.”[16]具体来讲,是对数学符号所表示的数、数量关系和规律的理解.应包括两方面的内容:“一是在实际情境中理解符号所代表的意义,并能解释代数式的意义;二是能从代数式、表格图像所表示的变量之间的关系中获取所需的信息,并能初步理解代数式、表格、图像之间的转换.”[4]“对于同样的数学符号语言,学生的理解结果存在一些不同,理解过程存在一定的差异.这些不同和差异主要体现在理解的广度、符号之间关系的理解、字母意义的理解等方面.”[16]可见,符号理解是符号意识的一个重要维度,可从理解的正确性、广度、深度、符号之间的转换等具体层面来分析学生的符号意识.
3.3 符号的运用(维度三)
数学符号的使用是数学表达和数学思考的重要形式,这里的符号运用指的是对数学对象的符号表示、符号运算、符号推理和符号思考.具体包括符号运用的主动性、正确性、复杂性、灵活性、多样性等方面.
4 小学数学符号意识分析框架的验证
分析框架建立后仍需对其合理性进行检验[17].构建小学生数学符号意识分析框架的重要目的就是在具体教学中,能在具体操作层面分析和评估不同学生的符号意识发展水平,进而进行有针对性的培养.所以研究检验框架合理性的基本思路为:以分析框架的具体成分为依据,编制测试题并实施测试[18],考察不同学生(年级、成绩、性别)在符号意识的不同维度(符号认识、符号理解、符号运用)方面是否存在显著差异.实验选取某小学1~6年级部分学生进行测试,发放试卷537 份,回收537份,其中有效卷为507份,有效率为94.41%.数据分析结果见表7~表9,结果分析如下.关于符号认识:符号认识在年级方面存在显著差异;符号认识在数学成绩方面存在显著差异;符号认识在年级与成绩交互性方面、在年级、性别与成绩的交互性方面均存在显著差异;符号认识在性别方面不存在显著差异.关于符号理解:符号理解在年级方面存在显著差异;符号理解在数学成绩方面存在显著差异;符号理解在性别方面不存在显著差异,同样在年级、性别、数学成绩之间的交互性方面也不存在显著差异.关于符号运用:符号运用在年级方面存在显著差异;符号运用在数学成绩方面存在显著差异;符号运用在性别方面不存在显著差异,但在年级与性别的交互性方面,存在显著差异;在其它交互性方面不存在显著差异.
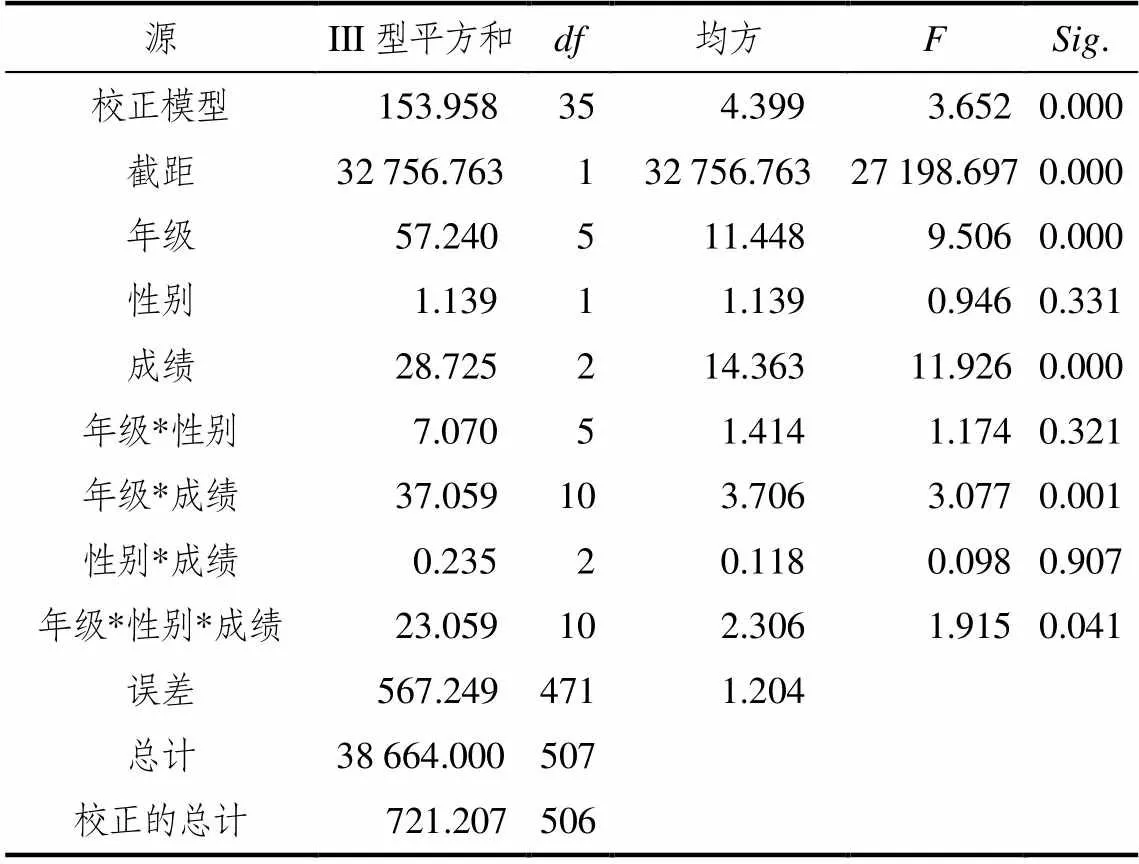
表7 不同学生在符号认识方面的方差分析
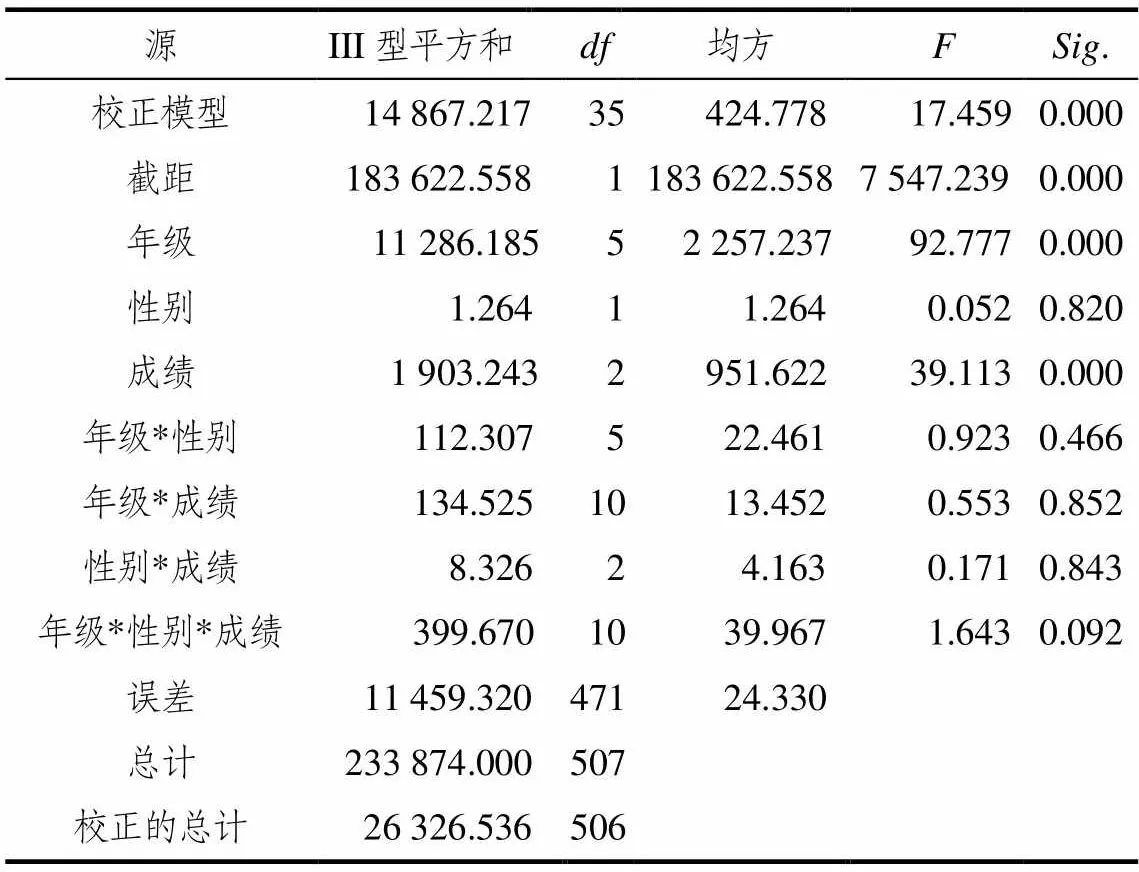
表8 不同学生在符号理解方面的方差分析
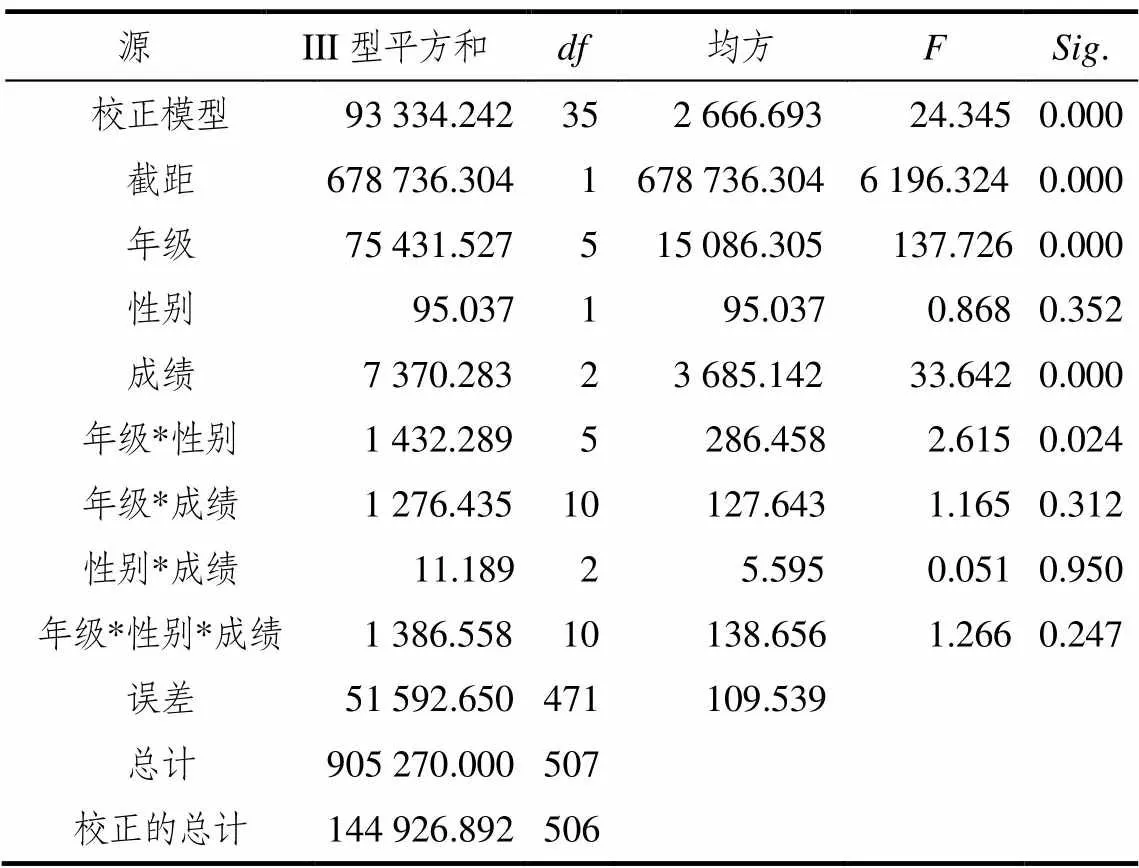
表9 不同学生在符号运用方面的方差分析
以上分析结果说明分析框架的维度和具体成分能反映出不同年级的学生、不同数学成绩的学生、不同性别的学生以及相互交互性在符号意识方面所表现出的差异.差异性说明该分析框架能够分析不同学生的数学符号意识发展水平,在具体教学实践中可以作为行为评估指标,具有可操作性和合理性.同时,关于上述研究结果和其它研究成果是基本吻合的.例如,汤强(2009)在博士论文“七~九年级学生数学符号语言的理解与表示”中得出结论——学生在符号理解和表示上的不同表现与他们所具有的学业水平是比较一致的.总的来说,学优生在很多方面都明显地优于中等生和学困生.刘瑶(2014)在硕士学位论文“初中生符号意识现状调查研究——以七年级为例”中得出结论——符号意识与数学成绩呈现高度直线正相关关系,初中生符号意识不存在性别差异[19].这也从另一方面说明分析框架具有其合理性.
5 结语
符号意识作为一种隐性的课程目标,需要一个科学的、合理的、可观察的、可操作的分析框架.李艳琴和宋乃庆认为:“可操作性定义是对小学低段数学符号意识最本质的揭示,是小学低段数学符号意识内涵维度的具体表现,也是小学低段学生数学符号意识培养策略研究的出发点.”[20]这个观点同样适用于小学其它阶段,这种具有操作性的分析框架有利于教师对数学符号意识本质的认识和理解,有利于为教师培养学生的符号意识提供具体和可行的途径.希望能给学生符号意识的有效培养提供有价值的参考.
[1] 朱立明,马云鹏.“数学符号意识”研究:内涵与维度[J].教育理论与实践,2015,35(32):6–8.
[2] 陶红强.小学生数学符号意识发展研究综论[J].小学数学教与学,2015(9):43–45.
[3] 中华人民共和国教育部.义务教育课程标准(2011年版)[M].北京:北京师范大学出版社,2012:6.
[4] 王林.小学数学课程标准研究与实践[M].南京:江苏教育出版社,2011:109.
[5] 张号,童莉,黄翔.数学符号从“感”到“意识”[J].数学教育学报,2014,23(1):100–102.
[6] 黄翔.数学课程标准中的十个核心概念[J].数学教育学报,2012,21(4):16–19.
[7] 王成营.数学符号意义获得能力研究[M].北京:清华大学出版社,2016:37.
[8] 朱立明,马云鹏.学生数学符号意识PORE评价框架的构建[J].数学教育学报,2016,25(1):84–88.
[9] 郑毓信.“数感”“符号感”与其它——《课程标准》大家谈[J].数学教育学报,2002,11(3):30–32.
[10] 邵光华.作为教育任务的数学思想与方法[M].上海:上海教育出版社,2009:74.
[11] 史炳星,马云鹏,唐复苏.在解决问题的过程中发展学生的符号感[J].数学教育学报,2002,11(2):57–60.
[12] 孔企平.小学儿童如何学数学[M].上海:华东师范大学出版社,2000:6–8.
[13] ARCAVI A. Symbol sense: Informal sense making in formal mathematics [J]. For the Learning of Mathematics, 1994 (3): 10.
[14] ZOM P A. Computer algebra and mathematical thinking [C] // Presentation at the 2nd International Conference on the Teaching of Mathematics, Hersonissos, 2002: 1.
[15] QUANTITY J F. On the shoulders of giants: New approaches to numeracy [M]. Washington D.C: National Academy Press, 1990: 1.
[16] 汤强.七~九年级学生数学符号语言的理解与表示[D].重庆:西南大学,2009:Ⅰ–Ⅱ.
[17] 裴昌根,宋乃庆,刘乔卉,等.数学学习兴趣测评指标体系的构建与验证[J].数学教育学报,2018,27(2):70–73.
[18] 张和平,裴昌根,宋乃庆.小学生几何直观能力测评模型的构建探究[J].数学教育学报,2017,26(5):49–53.
[19] 陶红强.小学生数学符号意识发展的实验研究[D].南京:南京师范大学,2016:38.
[20] 李艳琴,宋乃庆.小学低段数学符号意识的培养策略研究[J].数学教育学报,2016,25(5):28–31.
The Development of a Framework of Students’ Mathematical Symbolic Sense in Elementary School
TAO Hong-qiang
(Liyang Tangqiao Primary School, Jiangsu Changzhou 213300, China)
As a key competency of mathematics, symbolic sense warrants attention from mathematics educators. Given the importance of constructing a framework of student’s symbolic consciousness from specific behaviors, this study constructed such a framework from three dimensions (knowing, understanding, and application) which include 15 factors based on several previous studies that referred to the operational definitions of symbolic consciousness.
primary school; symbol consciousness; framework; dimensions
G421
A
1004–9894(2020)05–0041–05
陶红强.小学生数学符号意识分析框架的构建[J].数学教育学报,2020,29(5):41-45.
2020–03–03
江苏省常州市教育科学“十三五”规划第一批重点课题——小学生数学符号意识发展规律的实验研究(CJK-Z2018037)
陶红强(1982—),男,江苏溧阳人,中小学高级教师,主要从事小学数学教育的理论与实践、数学教学心理学研究.
[责任编校:陈汉君、陈隽]
