求解时谐涡流场离散系统分裂迭代法的参数改进

魏江超，马昌凤

(福建师范大学 数学与信息学院,福建 福州 350117)

0 引言

考虑如下的时谐涡流问题的耦合模型:

(1)

其中,E,H,Je分别是电场强度、磁场强度与涡流电流密度,Ω是3上的单连通的有界多边体，∂Ω为Ω的边界,ΩC与ΩI分别为Ω的导体区域与非导体区域,Γ为ΩC与ΩI闭区域的交集,n为Ω与Γ上指向ΩI的单位外法向量方向,介质的磁导率、介电常数、电导率和角频率分别用μ,ε,σ,ω表示,更详细的说明可见文献[1-2].

当非导电区域ΩI的第一贝蒂数为0时,利用有限元方法离散耦合模型(1),可以得到简单拓扑情况下的离散系统,当非导电区域ΩI的第一贝蒂数大于0时,我们也可以得到一般拓扑情况下的系统, 具体可见文献[3].一般情况下,我们会对简单拓扑等式两边左乘矩阵￡=Diag(-iI,-iI,-I,-I),则得到

(2)

其中,A1=MC-iSC,A2=SI+τB*BI, 并且MC为对称正定矩阵,SC与SI为对称半正定矩阵,BC与BI为行满秩矩阵,D为一个实矩阵,注意到实际上A2是一个对称正定矩阵.同样地，对于一般拓扑情况下的系统，两边乘以￡=Diag(-iI,-I,-I), 可以得到

(3)

在生活中,时谐涡流模型常常运用于模拟低频交流电的电磁现象.众多学者为了解决时谐涡流模型的离散模型提出了许多算法,如修正超松弛迭代算法与Uzawa-like算法[4],交替半正定分裂(APSS)迭代算法[5],正定与半正定分裂(PS)迭代方法[6],以及Bai等人提出了一类块交替分裂隐式(BASI)迭代算法[3].同时,为了高效地求解,也提出了许多预处理子,如维分裂预处理子[6]等.笔者在预处理分块交替分裂隐式(PBASI)迭代法[7]上做了进一步的改进,引入了新的参数β,同时研究了新的迭代算法的收敛性,给出了一种分裂情况下具体的计算步骤.

1 预处理分块交替分裂隐式迭代法

首先, 文中所考虑的广义鞍点矩阵如下:

(4)

其中,A∈Rm×m为正定矩阵,C∈Rn×n为Hermitian半正定矩阵,B∈Rm×n,(m>n).在文献[3]中首先给出了一种分裂如下：

A=(αI+P)-(αI-S)=(αI+S)-(αI-P)=P+S,

(5)

式中，

(6)

其中,A=P+S且P为一个正定矩阵,S为反Hermitian矩阵,B=B1+B2为矩阵B的一个分裂.从而进一步得到交替分裂隐式(BASI)迭代方法来求解鞍点问题(4)如下：

(7)

式中，V=Diag(V1,V2)为块对角矩阵,V1,V2为对称正定矩阵.并且给出了收敛分析如下：

定理1 假设广义鞍点问题(4)的系数矩阵A有(5)-(6)的分裂.V是对称正定的分块对角矩阵.当B的分裂B1和B2满足

时, 对于任意的α>0,给定任意初始值x(0)∈Cm×n,根据迭代格式(7),算法均收敛到问题(4)的精确解.

2 双参数的预处理分块交替分裂隐式(DPPBASI)迭代法

在本节中, 我们在原先的预处理分块交替分裂隐式迭代格式上进行了新的改进, 引入了第2个参数β,进行了新的迭代格式的收敛性分析,并且给出了在实际计算中的计算方式.

2.1 DPPBASI迭代算法与收敛分析

对于问题(4),我们对第1节中的预处理分块交替隐式迭代法进行改进，引入第2个参数β,进而可以得到如下算法:

算法1 对于广义鞍点问题(4)的系数矩阵A做(5)-(6)的分裂,给定任意的初始值x(0)∈Cm×n,对于k=1,2,3,…,使用下面迭代格式得到迭代序列{(x(k))}直至满足终止准则:

(8)

其中α>0,β>0,V=Diag(V1,V2)为对称正定的分块对角矩阵,V1,V2为对称正定矩阵.

可以简单地看出,当α=β时,TPPBASI迭代算法退化为PBASI迭代算法, 并且当α=β=1时,DPPBASI迭代算法退化为文献[3]提出的APSS迭代算法.下面我们给出算法的收敛性分析, 首先给出一个有用的引理.

引理1 假设矩阵A可分解为A=P+S, 其中矩阵P与矩阵S分别是Hermitian半正定矩阵与反Hermitian矩阵,若对给定的α>0有

(9)

则有ρ((βI+S)-1(βI-P)(αI+P)-1(αI-S))<1, 其中λmin与λmax分别是P的最小与最大特征值,ρ(Q)是矩阵Q的谱半径.

证明这里采用与文献[9]定理2类似的证明方式, 这里给出简单的过程如下：

(10)

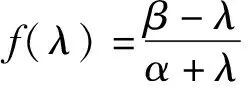
进一步,存在α,β*，其中λmin≤β*≤λmax,事实上β*是关于λminλmax,α函数,使得下列等式成立:

(11)

下面分3种情况讨论:

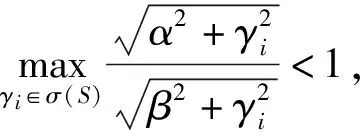
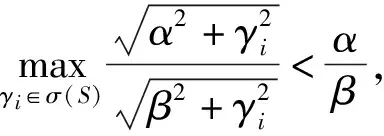
情况3 当β=α时,矩阵(βI+S)-1(βI-P)(αI+P)-1(αI-S)相当于BASI方法的迭代矩阵, 它是无条件收敛的, 所以等式自然成立.

综合上述3种情况, 容易得到定理结论.

下面我们给出算法的收敛性定理.

定理2 假设广义鞍点问题(4)的系数矩阵A有(5)-(6)的分裂, 其中矩阵P与矩阵S分别是Hermitian半正定矩阵与反Hermitian矩阵,V是对称正定的分块对角矩阵.对于任意α>0,若β满足

证明由算法1,可以得到DPPBASI方法的迭代矩阵T如下:

(12)

2.2 时谐涡流问题中TPPBASI算法的求解

在这小节中,将结合离散的时谐涡流问题的代数形式, 研究其简单拓扑和一般拓扑在TPPBASI算法下的具体实现.

2.2.1 简单拓扑情况下的算法

结合等式(2),广义鞍点问题(4)可以改写成如下形式:

(13)

其中，

进一步,可以做出分裂如下：

A=(αV+P)-(αV-S)=

(αV+S)-(αV-P)=P+S.

(14)

其中P，S由式(6)规定，V=Diag(V1,V2,V3,V4)，又V1,V2,V3,V4为对称正定矩阵且

容易验证P为半正定Hermitian矩阵,S为反Hermitian矩阵.

将上述分裂带入算法1, 我们知道每一步迭代都只需要求解两个线性方程组如下:

(15)

其中，

与

(16)

其中，

经过简单的计算, 我们可以得到该分裂迭代格式如下:

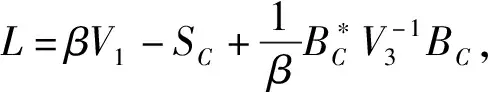
1)通过求解对称正定方程:

循环1)～4)直至满足终止条件.我们可以发现算法的主要计算量集中在步骤1)与步骤3),其中可以发现步骤1)求解的系数矩阵为正定Hermitian矩阵, 而步骤3)求解的系数矩阵为正定非Hermitian矩阵,因此在实际应用中可以考虑非精确求解方法.

2.2.2 一般拓扑情况下的算法

结合等式(3)与广义鞍点问题(4),可以有:

(17)

其中，

进而可以给出下面一种分裂:

A=(aV+P)-(αV-S)=

(αV+S)-(αV-P)=P+S.

(18)

其中，P,S由式(6)规定，V=Diag(V1,V2,V3)，又V1,V2,V3为对称正定矩阵且

容易验证P为半正定Hermitian矩阵,S为反Hermitian矩阵.

运用与简单拓扑情况下相似的做法,可以得出该分裂的迭代格式如下:

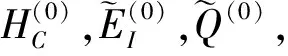
1)通过求解对称正定方程:

其中

循环1)～4)直至条件满足.

因此,可以发现算法的主要计算量集中在步骤1)与步骤3);同时,也可以发现步骤1)求解的系数矩阵为正定Hermitian矩阵,而步骤3)求解的系数矩阵为正定非Hermitian矩阵,因此在实际应用中也可以考虑非精确求解方法.