两类低重量线性码

陈 行,文 雯

(西华师范大学 数学与信息学院，四川 南充 637009)

0 引言

A0+A1x+…+Anxn.

重量枚举器中有A0=1，并且将序列(1,A1,A2,…,An)称为线性码C的重量分布.如果|{1≤i≤nAi≠0}|=t，就将线性码C称为t重码.

良好的代数结构是线性码的优点之一，所以它也是编码理论研究的热点之一.在研究线性码时，重点研究线性码的最小重量，因为最小重量不但可以用来计算信息在信道中传输时发生干扰的概率，还可以用来评价线性码的纠错能力.最小重量较低的线性码常常应用在结合方案[1]、认证码[2-3]、组合设计[4]和秘密共享方案[5]等领域.然而，线性码的重量分布很难被求出，仅仅有少数特殊的线性码的重量分布可以被完全求出.

文献[6]介绍了线性码的一般构造方式，设定义集为D={d1,d2,…,dn}⊆Fq，那么线性码可以由定义集构造出：

CD={(tr(xd1),tr(xd2),…,tr(xdn))x∈Fq}.

其中tr(α)=α+αp+…+αpm-1(∀α∈Fq)为从Fq到Fp的迹函数.研究[7]发现，只要通过选取合适的定义集，便可以使用上述构造线性码的方法得到最小重量较低的线性码.

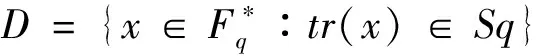
笔者在p|m的情况下，选取定义集为D={x∈Fqtr(x)=0,tr(x2)∈Sq}，由此构造出线性码CD={(tr(ax))x∈Da∈Fq}，其中p为奇素数，m>2.

1 预备知识

1.1 加法特征

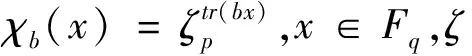
定理1[11]Fq上的加法特征满足正交性：

1.2 乘法特征

Fq上的乘法特征为：

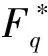
1.3 高斯和

2 线性码CD的重量分布

设T=|{x∈Fqtr(x)=0,tr(x2)=b2,tr(ax)=0}|,b∈Fq.对任意的a∈Fq，码字c(a)的重量为：

注：

1)n代表码字的长度;

定理2[8]符号定义如上，定义N(μ,v)={x∈Fqtr(x2)=μ,tr(x)=v,μ,v∈Fp}，则有：

1)当μ=0，v=0时,有

2)当μ=0，v≠0时，有

3)当μ≠0，v≠0时，有

4)当μ≠0，v=0，时，有

由4)，可以求出码字的长度n.当m为偶数时，n1=n=[(p-1)pm-2-p-1(p-1)Gm]/2；当m为奇数时，n2=n=(p-1)pm-2/2.

因此，当m为偶数时，有：

当m为奇数时，有：

已知有：

其中Ω1，Ω2，Ω3，Ω4分别如下：

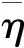
定理4[11]符号定义如上，若f(x)=a2x2+a1x+a0∈Fq[x]，a0≠0，则有

定理5 符号定义如上，如下成立:

1)当m为偶数时,

2)当m为奇数时,

Ω3=Gm.

证明由定理4，有

由定理3，结论成立.

定理6 符号定义如上，则有如下:

1)当m为偶数时,

2)当m为奇数时,

证明由定理4，有如下式子成立:

当m为偶数时，由定理3得

当tr(a2)=0时，

当tr(a2)≠0时，

综上，有

当m为奇数时，由定理3得

当tr(a2)=0时，

当tr(a2)≠0时，

综上，有

定理7 符号定义如上，有如下成立:

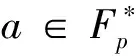
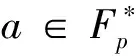
证明这里只给出m为偶数时，a=0时的重量的算法，其他情况类似.

a=0时,

定理8 符号定义如上，则线性码的重量分布如表1、2所示.

表1 m为偶数时，线性码重量分布

表2 m为奇数时，线性码重量分布

证明定理8给出了线性码所有的重量，定理2给出了每种重量的码字的个数.

3 结论

笔者选取了特定的定义集，得到了四重的线性码.该线性码有更小的重量，适用于构建身份验证代码，线性码特殊的重量分布可以解决一些特定攻击成功的概率.

致谢:感谢论文参与者对文章的贡献！