基于单常数Kubelka-Munk理论的棉纤维颜色预测

高新 潘如如 高卫东

摘要： 为解决混色棉纤维颜色预测效果较差、模型预测精度较低的问题，文章通过对Kubelka-Munk理论的分析，确定采用基于单常数Kubelka-Munk理论的配色模型对混色棉纤维进行预测。在明确此配色模型不足之处的基础上，提出了标准化映射的方法对模型进行适用性改进，消除极端K/S值对模型预测效果产生的不利影响，从而改善模型的颜色预测效果。通过试验发现，模型对混色棉纤维颜色预测的适用性有明显改善，改进后的单常数K-M模型对混色棉纤维颜色预测精度有大幅度提高。

关键词： 颜色预测;配色模型;棉纤维;标准化映射;Kubelka-Munk

中图分类号： TS193.1

文献标志码： A

文章编号： 10017003（2020）09003405

引用页码： 091107

DOI： 10.3969/j.issn.1001-7003.2020.09.007（篇序）

Cotton fiber color prediction based on the single constant Kubelka-Munk theory

GAO Xina， PAN Rurub， GAO Weidongb

（a.School of Textiles and Clothing; b.Key Laboratory of Eco-Textiles， Ministry of Education， Jiangnan University， Wuxi 214122， China）

Abstract：

In order to solve the problems of poor color prediction effect of mixed-color cotton fiber and the low accuracy of model prediction， it was determined that the color matching model based on the single constant Kubelka-Munk theory was used to predict the mixed-color cotton fiber. On the basis of clarifying the shortcomings of this model， the method of standardized mapping was put forward in this paper to improve the applicability of the model， eliminate the adverse effects of extreme K/S values on the prediction effect of the model， and thus improve the color prediction effect of the model. Through the experiment， it was found that the applicability of the model to the color prediction of mixed-color cotton fiber was significantly improved， and the improved single constant K-M model greatly improved the color prediction accuracy of mixed-color cotton fiber.

Key words：

color prediction; color matching model; cotton fiber; standardized mapping; Kubelka-Munk

收稿日期： 20191111;

修回日期： 20200820

基金项目： 国家重点研发计划基金项目（2017YFB0309200）

作者簡介： 高新（1993），男，硕士研究生，研究方向为数字化纺织技术。通信作者：潘如如，教授，prrsw@163.com。

色纺纱一般是指经特定工序混合加工纺制而成、含有两种或两种以上不同颜色纤维的纱线，具有特定外观色彩风格[1]。色纺面料因其具有宏观色彩丰富、立体感强等外观风格而被市场青睐，产品已由最初的麻灰色系列发展到彩色系列，从小色差素色品种发展到大色差混色品种，并形成了纺织行业中独具特色的色纺产业[2]。研究表明，当前制约色纺产业发展的主要因素是配色和混色[3]，多数色纺企业配色仍旧采用效率较低的人工配色方法，无法满足市场小批量、变化快的需求。

近年来，不断发展的计算机测配色技术可以缓解色纺企业配色难的困境。由于计算机测配色技术在织物印染加工的成功应用[4]，人们尝试将其应用于色纺产品的颜色预测，并提出了多个配色模型[5-7]，但是有色纤维与不同染料的混合，其呈色机理较为复杂，到目前没有理想的配色模型可以对色纺产品做出十分精确的颜色预测。在提出的配色模型中，基于Kubelka-Munk理论（简称K-M理论）的配色模型应用最为广泛，适用性也相对较好。在不同的假设前提下，基于K-M理论的配色模型可以分为单常数K-M模型和双常数K-M模型。Walowit等[8]将最小二乘法用于双常数K-M模型，使得模型对有色纤维的颜色预测更加便捷、准确。单常数K-M模型已成功应用于染料、颜料对面料着色的测配色中[9]，但是对有色纤维颜色预测的效果远不及双常数模型，到目前为止也没有较好的方法改善它在色纺测配色领域的适用性。

本文分析了单常数K-M模型在有色纤维颜色预测方面的不足，通过标准化映射方法改善单常数K-M模型的适用性，消除极端反射率对预测效果的不利影响，提高了单常数K-M模型对混色棉纤维的颜色预测精度。

1 单常数K-M模型

1941年，Duntley[10]提出了基于反射率加和的有色纤维混色模型，单色纤维混合后的光谱反射率等与各单色纤维的光谱反射率与其所占比例乘积的和。虽然该假设经试验证明不成立，但是试验结果却表明混色纤维光谱反射率与各单色纤维的光谱反射率存在一定的加和关系，而不是Duntley所认为的简单的线性加和关系。随后，众多学者在此假设的前提下提出了多个配色模型，其中基于K-M理论的配色模型也由此而来。1963年，Davidson等[11]将Kubelka-Munk理论与“色料加和混合定律”相结合，得到了Kubelka-Munk单常数理论，理论假设对于染色纤维着色剂的散射相比于纤维可以忽略，纤维上染前后其散射系数S基本不变。因此，基于单常数K-M理论的配色模型在对混色棉纤维进行颜色预测时，其过程如下：

首先，将单色纤维的光谱反射率转化为K/S值：

KS（λ）=[1-R（λ）]22R（λ）（1）

式中：λ为光照波长;R（λ）为纤维在波长λ下的光谱反射率;（λ）为纤维在波长λ处的色深。

然后，根据混色纤维中各单色纤维所占比例，将各单色纤维的K/S值按比例进行线性加和，得到混色纤维K/S值：

M（K/S）=∑ciKiS（2）

式中：M（K/S）为混色纤维的色深;S为纤维的散射系数;Ki第i种单色纤维的吸收系数;ci为第i种单色纤维所占比例，且有∑ci=1;i为混色纤维中单色纤维种类i=1，2，3…。

最后，将混色纤维的K/S值还原为光谱反射率，得到模型预测光谱反射率。

2 标准化映射

在数据处理与分析之前，通常需要先将数据标准化，利用标准化后的数据进行数据处理与分析，有利于发掘数据之间的潜在联系，提高数据处理效率。数据标准化的方法有很多种，常用的有“min-max标准化”“Z-score标准化”和“按小数定标标准化”等。其中min-max标准化方法是对原始数据进行线性变换，min和max分别为属性R的最小值和最大值，将R的一个原始值R0通过min-max标准化映射到指定区间中的值R1，其具体公式如下：

t=u-dmax-min（3）

R1=d+（R0-min）×t（4）

式中：t为映射系数;u为映射后的最大值;d为映射后的最小值;max为映射前最大值;min为映射前最小值。

3 试 验

3.1 材 料

选用红、黄、蓝、黑、白5种颜色的棉纤维进行试验，其光谱反射率如图1所示。

3.2 混色样本的制备

采用N288型打样机（青岛源泉机械有限公司）对有色棉纤维进行混合、梳理，将红、黄、蓝、黑、白5种有色纤维中任意两种颜色混合制成两色混色样本，将红、黄、蓝三种彩色纖维共混制成三色混色样本。两色混色样本中各单色纤维所占比例从10%～90%，比例变化步长为10%;三色混色样本中各单色纤维所占比例从5%～90%，比例变化步长为5%。制备混色样本时，将不同单色纤维按一定比例混合后经梳棉机重复多次梳理，以使纤维混合均匀，然后将梳理过的纤维团放入箱子中压平，以便后续测色。本文共制得90个两色混色样本，171个三色混色样本。

3.3 样本光谱反射率的测定

将压过的混色样本对折两次，使纤维团达到一定的厚度以保证样本不透光，然后经Datacolor 650分光光度测色仪测色。Datacolor 650的测色条件为标准D65光源，测色范围为400～700 nm，间隔10 nm，标准观察者10°视场，测色孔径30 mm，设置仪器测色允差为0.1。样本测色时，对每个样本选取4～8个不同位置进行测量，以减小测量误差。

4 单常数K-M模型的适用性优化

4.1 标准化预处理

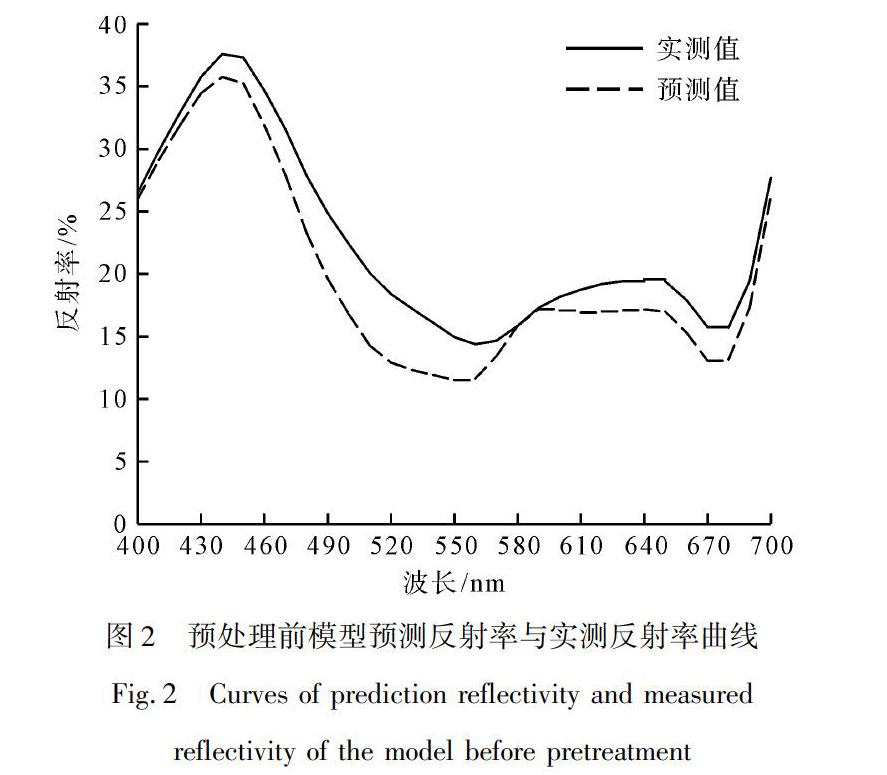
通过试验发现，即使将纤维的光谱反射率转化为K/S值后，混色样本的K/S值与各单色纤维的K/S值之间仍然没有较好的线性加和关系，导致模型预测反射率与样本实测反射率之间有较大差异。图2为30%红色纤维与70%蓝色纤维混合的两色混色样本（30R/70B）的实测光谱反射率与模型预测光谱反射率对比曲线。从图2可以看出，预测值虽然已经和实测值有较为相似曲线趋势，但是在每个波段的差值过大。而经试验验证得知，若将单色纤维的光谱反射率先经min-max标准化预处理后再代入单常数K-M模型进行颜色预测，混色纤维的K/S值和各单色纤维的K/S值之间的线性加和关系得到明显改善，进而使得模型预测光谱反射率更加接近实测光谱反射率，优化后模型对同一样本的预测效果如图3所示。

因此，本文决定通过min-max标准化的方法对单色纤维进行预处理，优化单常数K-M模型对混色棉纤维的预测效果，提高模型的预测精度。在预处理时，为方便计算，将式（3）中反射率的最大值max与最小值min分别设为100%和0，因此可将式（3）（4）合并，得到式（5），即：

R1=d+R0×（u-d）（5）

式中：R0是纤维实测光谱反射率;R1是R0的映射值。

4.2 确定映射范围

通过遍历法求解最佳映射范围，即选取90个三色样本的实测光谱反射率作为遍历数据。遍历时，u、d起始值分别设为0.01和0.99，变化步长为0.01，d值按步长递增，u值按步长递减。采用CIEDE2000色差公式[12]求解模型预测值与样本实测值之间的色差，当两者的色差值最小时，确定每个样本的最佳u值和d值。样本的最佳d值分布如图4所示，可见样本最佳d值在区间[0.05，0.07]内占比较大;同样可以得出，样本最佳u值在区间[0.78，0.83]内占比较大。

通过算法得出在不同映射范围下三色样本实测值与模型预测值之间的色差和，具体数据如表1所示。不同d值对彩色样本的色差和影响较大，其最佳d值为0.06;不同u值对彩色样本的色差和影响较小，90个样本在区间[0.78，0.81]内的差值不超过1，但是当u值为0.81时，样本的最大色差值为088，而其他u值对应的样本最大色差分别是1.05、0.97和0.90，因此确定样本的最佳u值为0.81。

5 预测效果及分析

本文将所有两色和三色混色样本分为训练集和测试集两个部分，其中训练集是90个三色混色样本，测试集包括所有两色混色样本和81个三色混色样本。首先对训练集中的样本进行试验，确定模型的标准映射区间为[0.06，0.81]，然后将测试集中的样本数据代入模型检验模型的适用性和预测精度。

5.1 三色样本预测效果对比

通过算法分别对三色样本的测试集和训练集进行模型预测，样本实测值与模型预测值之间的色差越小说明模型的预测效果越好，90个训练样本和81个测试样本的预测效果如表2所示。相对于测试集，训练集中三色样本的色差在0.6以下的样本占比较大，高于0.6的样本较少，模型对训练集的预测效果较好。从整体来看，模型对训练集和测试集中的三色样本的预测效果相差不大，所有三色样本的色差都在1以下，因此改进后的单常数K-M模型对三色混色样本的预测效果较好。

5.2 两色样本预测效果分析

表3是模型对所有混色样本预测效果的数据对比。由表3可知，模型对红-蓝、黄-蓝和红-黄等不含有黑色或者白色纤维的两色样本的预测效果较好，其色差均值和最大色差与模型对三色样本的预测效果相差不大。但是含有黑色纤维的所有两色样本的色差均值和最大色差值相较于三色样本都有不同程度的增大，模型的预测效果变差，同时对含有白色纤维的两色样本的预测效果出现波动，对白-蓝和白-红混色样本的预测效果较好，对白-黄混色样本的预测效果较差。

对单常数K-M模型改进的中心思路是通过预处理将单色纤维的光谱反射率映射到特定区间后再代入模型进行预

测，但是通过试验发现，对于不同种类混色纤维的颜色预测，其最佳映射区间也有所差异。从表3数据可以看出，在现有映射区间内，模型对含有黑色和白色纤维的混色样本的预测效果相对较差，因此决定将含有黑白纤维的混色样本作为遍历数据进行二次遍历试验，得到适用于含有黑白纤维混色样本的映射区间。

通过试验确定适用于含有黑白纤维的混色样本颜色预测的映射区间为[0.08，0.91]，在不同映射区间下，模型对含有黑色或白色纤维的混色样本的预测效果对比数据如表4所示。表4中，选取的混色样本都是模型在P1区间内预测效果较差的样本，但是在P2区间内，模型的预测精度有较大的提高。同时模型对含有黑色纤维的两色混色样本的预测时，其色差均值下降至0.56，样本的最大色差下降到0.94。此外，与在P1映射区间下的预测效果相比，模型在P2区间下对含有白色纤维的两色混色样本的预测效果也有不同程度的改善，白-蓝和白-红混色样本的色差均值和最大色差都有所下降，白-黄样本的色差均值和最大色差分别降到了0.77和095。

综上所述，针对不同种类的混色样本，选择不同的映射区间，优化单常数K-M模型的预测精度和适用性。在映射区间[0.06，0.81]内，模型对三色混色样本、红-黄、红-蓝及黄-蓝两色混色样本的预测效果较好，在映射区间[008，0.91]内，模型对含有黑色或者白色纤维的两色混色样本的预测精度较高。因此，将两个映射区间同时应用于改进后的单常数K-M模型，解决了单一映射区间下模型的适用性较差的问题，在保证模型有较高的预测精度前提下，使得模型对不同种类的混色样本预测时，样本的色差可以降到1以下。

6 结 语

本文将标准化映射的方法用于单常数K-M模型对混色棉纤维的颜色预测，并取得了较好的预测效果，模型预测精度有明显的提高。改变了单常数K-M模型无法应用于有色纤维颜色预测的现状，提出了对纤维光谱反射率进行预处理的新思路，为色纺配色模型的优化提供了新方法，有利于拓展Kubelka-Munk理论在纤维配色领域的适用性研究。

参考文献：

[1]金亚琪， 邹专勇， 许梦露， 等. 色纺纱产品开发现状及技术发展需求[J]. 棉纺织技术， 2012， 40（12）： 65-68.

JIN Yaqi， ZOU Zhuanyong， XU Menglu， et al. Development status and techology development demands of colored spun yarn[J]. Cotton Textiles Technology， 2012， 40（12）： 65-68.

[2]袁理， 代乔民， 付顺林， 等. 基于原色纤维混配色織物的呈色特性与影响因素分析[J]. 纺织学报， 2018， 39（10）： 38-43.

YUAN Li， DAI Qiaomin， FU Shunlin， et al. Coloration characteristics and influencing factors of colored spun fabric based on primary-color fibers blending[J]. Journal of Textile Research， 2018， 39（10）： 38-43.

[3]严旭新， 黄玉强， 于文菡， 等. 新型色纺精细混棉工艺流程研究[J]. 棉纺织技术， 2015， 43（6）： 49-52.

YAN Xuxin， HUANG Yuqiang， YU Wenhan， et al. New fine blending process procedure study of colored spinning[J]. Cotton Textile Technology， 2015， 43（6）： 49-52.

[4]李戎， 宋阳， 顾峰. 基于Stearns-Noechel模型的纤维光谱配色算法[J]. 纺织学报， 2007， 28（1）： 77-80.

LI Rong， SONG Yang， GU Feng. Spectrophotometric algorithm of pre-colored fiber based on Stearns-Nochel model[J]. Journal of Textile Research， 2007， 28（1）： 77-80.

[5]STEARNS E I， NOECHEL F. Spectrophotometric prediction of color of wool blends[J]. American Dyestuff Reporter， 1944， 33（9）： 177-180.

[6]FRIELE L F C. The application of color measurement in relation to fiber-blending[J]. Journal of Textile Institute， 1952， 43： 604-611.

[7]AMIRSHAHI S H， PAILTHORPE M T. Applying the Kubelka-Munk equation to explain the color of blends prepared from precolored fiber[J]. Textile Research Journal， 1994， 64（6）： 357-364.

[8]WALOWIT E， MCCARTHY C J， BERNS R S. An algorithm for the optimization of Kubelka-Munk absorption and scattering coefficients[J]. Color Research & Application， 1987， 12（6）： 340-343.

[9]车江宁. 有色纤维测配色研究[D]. 上海： 东华大学， 2002.

CHE Jiangning. Research on Color Measurement and Matching of Colored Fiber[D]. Shanghai： Donghua University， 2002.

[10]DUNTLEY S Q. The prediction and control of colored fiber blends by optical mixing[J]. American Dyestuff Reporter， 1941， 30： 689-700.

[11]DAVIDSON S R， KING D. Effect of particle size on photoacoustic signal amplitude[J]. Analytical Chemistry， 1984， 56（8）： 1409-1411.

[12]鄭元林， 刘士伟. 最新色差公式： CIEDE2000[J]. 印刷质量与标准化， 2004（7）： 34-37.

ZHENG Yuanlin， LIU Shiwei. The latest chromatic aberration formula： CIEDE2000[J]. Printing Quality and Standardization， 2004（7）： 34-37.