微观气象条件下风力发电机组塔架载荷响应分析

李成晨，张文彬,2，刘晓辉，卓 然，宋 珂

(1.许昌许继风电科技有限公司，河南 许昌 461000) (2.国家电投集团河南新能源有限公司，河南 郑州 450001)

随着高平均风速、低湍流优质风区的剩余量越来越少[1]，目前风电持续向大风轮直径、大单机容量、高塔架方向发展，以此提高风资源的利用程度。而随着塔架高度的增加，在兼顾塔架经济性的基础上必然会导致塔架固有频率降低，因此研究作为支撑结构的塔架在不同情况下的动力学响应对保证机组的安全可靠性尤为重要。

近年来国内外很多学者就塔架的动态响应开展了相关研究：赵艳等[2]使用基于数据驱动的随机子空间法识别了机组一阶自振频率和阻尼比，研究了风力机在启、停机过程中的振动特征，并基于Sommerfeld效应解释了风力机启、停机过程的不同振动效应；孙铁雷等[3]基于有限元法研究了塔架的暂态响应，发现脉动风载作用下塔架的1阶振型为主要振型，3阶振型以上的分量对机组的影响基本可以忽略不计；张丰豪等[4]同样采用有限元的方法研究了湍流风况下塔架弯曲、扭转固有振型特征，分析了结构阻尼对塔架振动的影响，结果表明随着阻尼的增加，塔架1阶弯曲振动主导作用减弱，振动特征主要受外界风载所控。

塔架的固有频率受塔架本身结构参数和外部机头重心位置及地基刚度的影响，不同固有频率塔架的动力学响应差别较大[5]，因此本文基于风电行业专业载荷计算软件Bladed结合实测风速数据和理论风谱模型确定湍流风模型[6]，分别从时域和频域两个方面考虑不同塔架1阶固有频率和微观气象条件下的塔架结构动力学响应特性，研究不同塔架结构参数和基础扭转刚度信息对塔架固有频率的影响规律。

1 建模和频率分析

塔架的固有振型和频率主要取决于塔架本身的结构特点(如直径、壁厚及高度)，其中受高度影响较为显著，同时也受风电机组机头质量、重心位置、地基刚度等因素影响。本文主要从塔架结构特点、机头质量以及地基刚度等方面对塔架固有频率和振型开展研究分析。

1.1 建立塔架模型

本文在对不同高度、底部直径及厚度的塔架进行建模时，将顶部机舱和风轮的质量简化为偏心质量块，将爬梯、电缆、平台、法兰及螺栓等简化为附件质量点。根据某厂家提供的2 MW风力发电机组设计参数，建立的Bladed和ANSYS塔架模型如图1所示，表1为风电机组设计参数。

表1 仿真机组总体设计参数

图1 塔架模型示意图

塔架模型结构参数主要包含底部直径(假设顶部直径恒定为2.9 m)、厚度、高度等，本文针对塔架结构参数和基础扭转刚度建立分析模型，模型参数详见表2，其中塔架厚度变量1～4采用均匀厚度模型，变量5～7的厚度按照曲线1～3分布情况建模，如图2所示。表3给出了塔架Q355的材料参数。

图2 筒壁厚度随高度分布图

表2 塔架几何参数

表3 塔架材料属性

1.2 模态分析

参照表2中的塔架结构参数，搭建不同几何尺寸的塔架模型，采用单因素变量法[8]，与对照组比对、分析不同塔架模态频率和振型。塔架1阶固有频率随塔架结构参数的变化情况如图3所示。

图3 塔架1阶固有频率随塔架结构参数的变化情况

将图3(a)、(b)、(c) 所示的3个散点图绘制到一张图表中，将高度、外径和壁厚与塔架1阶固有频率进行曲线拟合，其中横坐标在示意厚度时数值单位为mm，示意直径时单位为dm，示意高度时单位为m，如图4所示。

图4 塔架1阶固有频率与塔架几何参数关系

由图4可知：

1)塔架1阶固有频率随高度的增加呈近似指数趋势降低，随底部直径的增加呈对数趋势增加，随壁厚的增加呈对数趋势增加，其中底部直径的系数远大于壁厚。随着塔架高度的进一步增加，仅增加壁厚对提高塔架频率作用不明显，主要原因是壁厚会导致塔架质量增加而降低塔架频率。增加塔架高度时可以通过增加塔架底部直径来缓解因高度增加导致的频率降低，但底部直径的增加会引发运输、施工难度加大及质量增加较多等问题。近年来出现的分片式塔架能够在综合考虑加工运输和质量增加等方面实现较优的方案。

2)基础扭转刚度相当于增加了塔架一端的自由度，导致塔架1阶固有频率降低，从图3(d)的仿真结果看：当基础扭转刚度大于7.0E+11 N·m/rad时，塔架的频率基本没有变化，可以看作纯刚性基础；在刚度为7.0E+10～7.0E+11 N·m/rad时，塔架的固有频率直线下降；在刚度为6.0E+10～7.0E+10 N·m/rad时，塔架频率呈平缓下降趋势；在刚度低于5.5E+11 N·m/rad时塔架频率线性下降。结合实际经验，基础扭转刚度一般选择在6.5E+10 N·m/rad附近，这样会使塔架1阶固有频率降低约5%，此外塔架设计过程中还需要考虑基础扭转刚度的影响。

从“反补贴税的征收”到“双重补贴”———从中美贸易案的发展看中国“双反”问题的演进与特色…………李 季,卡玛拉·达沃(KamalaDawar)

对照组塔架1～3阶模态振型如图5所示，由图可知,1阶振型为左右或者前后振型，最大变形出现在塔架顶部；2阶振型为左右弯曲和前后弯曲，最大形变位置出现在塔架中上部；3阶振型为弯扭振型，存在2个或2个以上形变极值点，形变极点数量随塔架频率的降低而增多，其中传统钢制塔架主要的危险振型是1阶振型，而柔性塔架的主要危险振型为弯曲振型。

图5 塔架1～3阶振型

2 基于Bladed载荷响应分析

通过分析不同塔架1阶固有频率、不同微观气象条件下塔架的动态响应，结合第1章中塔架的模态振型，即可确定塔架的主要危险方向，在设计过程中可以通过局部加强或者结合现场实测数据对塔架进行控制加阻或者在某一振动幅值较大频点处增加阻尼器来减缓塔架的疲劳损伤程度，从而保证机组的长期平稳、安全运行。

2.1 载荷响应仿真试验设计

载荷响应仿真试验采用单因素试验方法，并设置标准对照组，各因素变量的设计方法基于目前风场常见微观气象条件，对照组和各试验因素的变量见表4。其中塔影效应采用常见的潜流模型，通过改变直径修正系数来改变塔影作用强度。进行仿真分析时，采用额定以上风速来研究叶片桨距角变化对塔架载荷响应的影响。

表4 Bladed仿真试验因素对照表

2.2 不同塔架结构下动力学响应分析

由第1章可知,不同塔架结构参数会导致塔架固有频率发生变化，根据表4的仿真变量组合，分别仿真不同塔架1阶固有频率下极端载荷、极端位移变化情况，然后对时序载荷谱做FFT(fast Fourier transform)分析出振动能量较大频点，如图6所示。

1)从图6(a)可知，塔架固有频率在机组1倍转频附近(0.207 Hz)时塔架载荷明显增加，振动位移幅值较远离1倍转频的机组增加3.6倍，此结论与频谱分析结论一致，详见图6(b)所示0.250 Hz附近，固有频率为0.206 Hz塔架的振动能量是0.260 Hz频率以上塔架的9.8倍。从时序载荷(详见图6(c))可知,0.260 Hz塔架载荷波动幅值明显高于其他频率塔架，0.178 Hz塔架载荷波动次之，0.260 Hz以上塔架载荷波动基本相同。

2)对于不同塔架的固有频率，塔架左右方向的载荷响应高于前后方向，详见图6(a)和6(c)。当频率距离机组1倍转频较近时会在左右方向产生较大的振幅，载荷幅值波动较大，疲劳损伤较大，长时间运行会因振动能量积累产生共振，在设计过程中应避免。

2.3 微观气象条件下载荷响应分析

根据表4的载荷仿真方法，统计塔顶左右和前后方向的扭矩和位移绝对值最大值，然后对时序载荷谱做FFT分析出振动能量较大频点，如图7～10所示。图中：Mx为塔顶左右方向扭矩,My为塔顶前后方向扭矩,disTTs-s为塔顶左右方向位移,disTTf-a为塔顶前后方向位移。

图7 不同湍流下塔架载荷响应

图8 不同风剪下塔架载荷响应

图9 不同塔影系数下塔架载荷响应

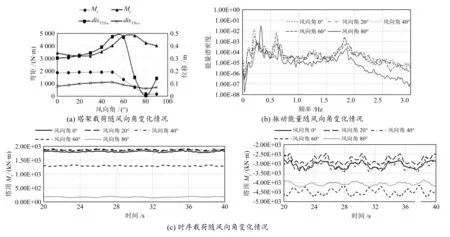
图10 不同风向角下塔架载荷响应

从图可知：

1)湍流强度。

湍流强度反映了风速和风向变化的紊乱情况，塔架前后方向对湍流强度的响应高于左右方向，且随着湍流强度的增加塔架载荷和振动位移急剧增加，详见图7(a)。振动能量较大的频点发生在机组1倍、3倍和9倍转频处，对0～0.5 Hz的频谱放大可以看出,随着湍流强度的增加，产生的激励频率与塔架的1阶固有频率相近,从而导致载荷逐渐增加，振动幅值逐渐变大，与图7(a)的趋势一致。

2)风剪系数。

风剪系数表征了风速随高度变化情况，风剪系数越大，同一高度差下风速差别越大，其主要影响轮毂中心处的弯矩。从图9(a)可知,塔架弯矩会随风剪系数的增加而降低，对于塔架来说，主要原因是风轮平面如圆盘，而风轮迎风面的风与叶片翼型产生升阻作用的耦合，对塔架产生推力，当风剪系数增大时风轮迎风面的风能降低，推力作用减小，故塔架弯矩My随风剪系数的增加而减低，风剪系数对塔架弯矩的频域影响较小。

3)塔影。

塔影为因风机塔架的存在而导致的稳态风场畸变，形成原理类似堵塞效应。塔架、叶片与来流风风向的相对位置使风机分为上风向和下风向机组，其中塔影效应对下风向机组影响较大。在仿真分析中常用的分析模型有潜流模型、塔架尾迹模型及组合模型，其中上风向机组多采用潜流模型，本文采用潜流模型，塔影修正系数A从0增加至2。

假设距离塔架无穷远处纵向风速为v0，气流绕过直径为D的圆柱状物体周围时层流不可压缩，则与塔架轴线前方距离为z、左右距离为x位置处风速为：

v(x,z)=Av0

(1)

(2)

风轮直径较小机组的z一般大于x，塔影修正系数A≤1。从图9(a)可知，塔影系数为0～1时，弯矩几乎没有变化；当塔影系数增大至2时，塔架弯矩My有所提高。从图9(b)可知，随塔影系数的增大，塔架及转频3倍、6倍、9倍频点处振动能量急剧上升。从图9(c)可知，当塔影系数增大至2时，塔架弯矩的振动幅值增大，其对塔架极限载荷影响较小，对塔架的疲劳损伤影响很大。从式(2)可知，随着风轮直径的增大，z保持不变的话，塔影修正系数会逐渐增大，对机组的疲劳损伤作用将进一步增强。

4)风向角。

为衡量风向对机组载荷的影响，将偏航系统锁定，仿真不同风向角对塔架弯矩响应的影响，其对塔架载荷的影响如图10(a)所示。塔架俯仰极限弯矩和前后极限位移随风向角的增大先增大后减小，在60°风向角附近达到极限，塔架弯矩Mx在0°～50°风向范围内变化较小，在风向角为50°～80°时载荷降低，超过80°后载荷有所提升。产生此现象的主要原因,是随着风向角的增大,振动主要能量向高频偏移，远离机组1倍转频范围,使得载荷和振动位移降低，但如果机组在实际运行过程中出现与该频次较接近的外部激励,会导致较大载荷出现。从图10(c)可知,随风向偏差增加,载荷呈降低趋势的主要原因是对风偏差导致机组出力降低。

3 结论

1)本文对塔架结构参数对塔架1阶固有频率的影响开展了相关仿真拟合研究，表明固有频率随高度的增加呈近似指数趋势降低，随底部直径和壁厚的增加呈对数趋势增加，但底部直径的比例系数远高于壁厚。因此，随塔架高度的进一步增加，靠提高壁厚增加塔架1阶固有频率作用不明显，可以通过增加塔架底部直径来缓解因高度增加导致的频率降低，但底部直径的增加会存在运输、施工难度加大及质量增加较多等问题，需综合考虑。

2)对于不同塔架的固有频率，塔架左右方向的载荷响应高于前后方向，当风电场出现较多的左右振动过大故障时需要重新对塔架固有频率进行测试标定，防止因基础变化、机头重心位置偏移、塔架偏心等产生的频率偏移导致机组载荷响应过大。

3)对不同微观气象条件下塔架载荷响应的研究表明：湍流、塔影和风向会对塔架载荷响应产生一定频次的扰动，其中以湍流强度尤为明显。本文的研究中外部激励没有与塔架固有频率相近，因此未出现共振情况，载荷水平也较低。实际风场中可以根据风场风资源情况对塔架控制加阻降低环境激励对塔架载荷响应的不利影响，具有一定的参考意义。