舍里甲大桥施工控制分析

2020-10-27白应华杨启萌余天庆

湖北工业大学学报 2020年5期

白应华, 杨启萌, 余天庆

(湖北工业大学土木建筑与环境学院，湖北武汉 430068)

随着我国经济的迅速发展，基础建设的步伐越来越快。其中桥梁建设是我国基础建设过程中不可或缺的一份子。系杆拱桥因其优美的造型和良好的力学性能，得到越来越多建设者的青睐[1-3]。随着桥梁跨度的增加，桥梁施工控制的应用在桥梁建设中越来越广泛，主跨跨度为200 m的上海柳港大桥是成功应用施工控制方法的典型案例[4]。近年来，有很多学者对拱桥的施工控制进行了研究：杜淼[5]以捞刀河大桥为例研究了复式钢箱中承式拱桥的施工受力；杜海龙等[6]研究了超大跨径拱桥的施工控制方法；刘俊杰[7]对大跨度拱桥吊杆张拉施工技术进行了研究。但是由于不同桥梁的造型和建设环境的不同，使桥梁具有独特性，所以目前施工控制在大跨度桥梁的应用还需完善。成熟的施工控制经验和监测手段是保障桥梁建设安全性和成桥合理性的关键。

1 工程概况

舍里甲大桥为钢结构下承式钢箱拱桥，位于南昌市经开区，主桥全长120 m，主梁由正交异性板钢箱梁构成，钢拱肋采用二次抛物线作为拱肋线形，拱顶预拱度设为45 mm。舍里甲大桥主梁采用双箱单室钢箱梁，梁顶宽33.5 m，支座处中心梁高3.5 m。采用顺桥向单吊杆体系，预应力钢绞线吊杆顺桥向和横向吊杆间距分别为4 m和0.5 m。8组预应力钢绞线系杆布置于主跨钢梁内和拱脚处。拱肋、钢箱梁先在工厂通过分阶段预制后，沿横断面分块进行运输，然后在现场通过吊装，吊装至临时墩进行拼装。舍里甲大桥拱肋梁采用支架架设的施工方案进行拼装，保证成桥后的线形与设计线形相吻合。吊杆抗拉强度为1860 MPa，钢结构主桥材质为Q345D。

2 施工控制方法

施工控制方法是在提出理想状态下的施工阶段控制参数后，结合施工过程中得到的实测数据，对结构计算影响较大的设计参数进行研究分析。依据设计要求，采取合适的方法对桥梁施工过程中所需要的控制量进行预测和监测，指导桥梁施工过程，保证最后成桥状态满足设计要求。

3 有限元计算

3.1 有限元建模

使用MIDAS/Civil 建立舍里甲大桥的全桥模型，运用梁格法[8]建模。空间梁单元考虑了截面剪切变形对结构受力的影响，主拱圈和主梁都用该梁单元模拟计算，采用桁架单元对吊杆和系杆进行模拟，全桥共划分1115个单元。支座与主梁通过弹性连接的方式进行连接，对施工过程中主梁支撑与拱肋支架通过在桥面节点处设置节点弹性支承进行模拟，利用MIDAS/Civil的激活与钝化功能实现主梁支撑与拱肋支架的搭设与拆除的模拟，吊杆合理成桥索力通过MIDAS/Civil 自带的未知荷载系数法求得，吊杆索力以初拉力的形式施加。图1为舍里甲大桥有限元模型。

图1 舍里甲大桥有限元模型

3.2 有限元计算结果分析

选取成桥阶段有限元计算结果进行分析研究。

1)位移由图2成桥阶段的桥梁竖向位移图所示，拱肋在拱顶处产生向下最大位移，位移值为19.5 mm。主梁边纵梁跨中处发生最大的向上竖向位移，位移值为56.9 mm。

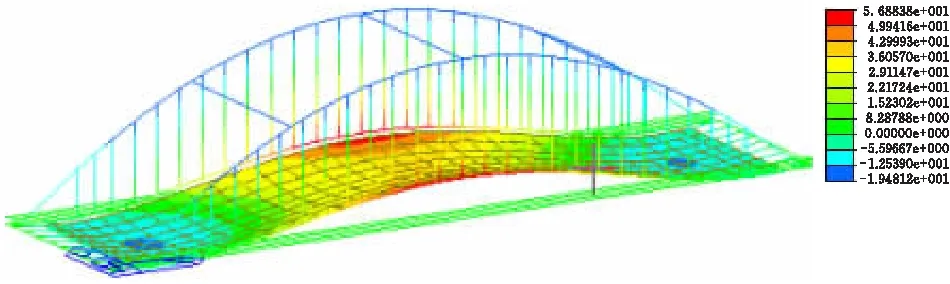
图2 成桥阶段竖向位移

2)应力由图3成桥阶段的应力图可知，拱肋轴向最大压应力为59.4 MPa，主梁最大拉应力为69 MPa。

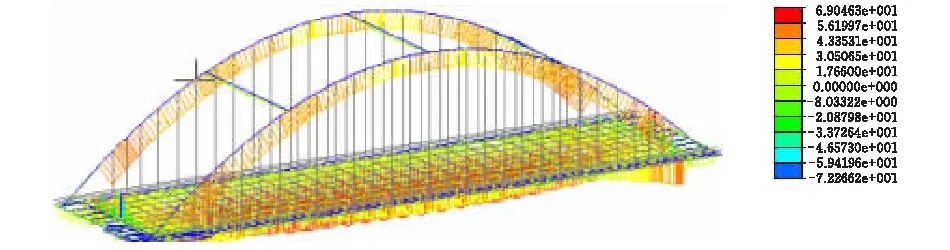
图3 成桥阶段应力

4 施工控制内容

4.1 拱肋线形控制

为减小拱肋线形误差，拱肋通过在工厂预制后运送到施工现场，并通过支架法进行拼装。在施工过程中，为保证拱肋的施工线形与计算线形的误差在设计允许范围之内，在拱肋节段接头位置处顶面内边缘的布置测点，通过全站仪对拱肋标高和拼装轴线进行监测并获得实时的监控数据。拱肋拼装现场如图4所示。

图4 拱肋安装现场图

这里拱肋的施工预拱度的设置考虑拱顶处的预拱度值，按二次抛物线分配法[9]进行分配。由二次抛物线分配法计算拱顶总挠度δ为

δ=δ1+δ2

其中：δ1为恒载挠度，δ2为1/2活载挠度

通过有限元计算得到挠度δ1=19.5 mm，δ2=11.1 mm。由二次抛物线分配法计算抛物线方程为

得到预拱度曲线如图5所示。

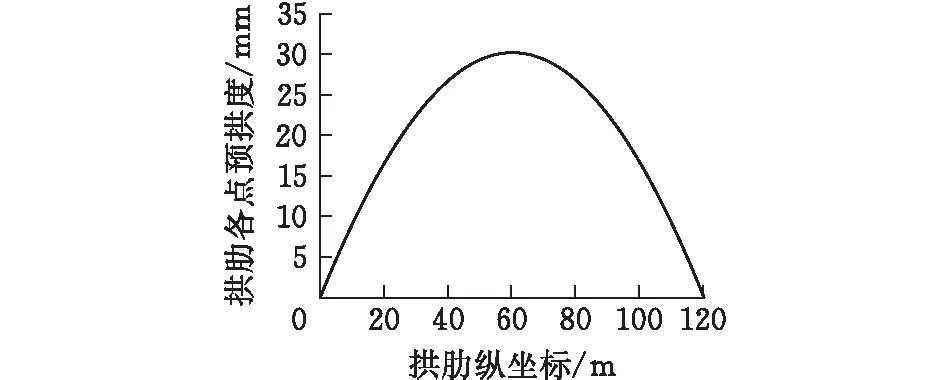
图5 拱肋曲线各点预拱度

拱肋线形的控制在设计曲线的基础上，加上各点的预拱度进行搭设，在施工过程中监控各点线形变化，保证最后成桥线形满足设计要求。

4.2 应力控制

系杆拱桥施工过程复杂，及时、准确了解施工过程中主梁和拱肋应力变化，不仅可以起到安全预警的作用，同时可以对理论进行校核，为施工控制提供依据。通过无线采集系统进行应力监测，该监测系统解决了传统人工巡检应力测试工作量大、测试周期长等缺点，扩展了应力测试的领域。同时，应力监测时记录气温、桥面特殊施工荷载等因素，为理论设计优化与预测提供更加准确的数据。

4.3 吊杆索力控制

吊杆索力是桥梁设计中的重要参数，主梁的线形和主梁内力分布可以直接被索力大小影响。利用影响矩阵法[10]进行吊杆索力控制，首先在模型中只进行吊杆安装，而不进行张拉，在二期和恒载作用下求得1-14吊杆索力：

F0=[819.5 407.2 404.8 530.4 535.4 535.5 526.4 525.3 528.2 525.2 527.2 527.7 531.2]

当模型计算不计二期重量和自重时，给吊杆1单位力，在Midas/Civil中得到吊杆1单独作用时对其他吊杆的影响量，记为A1=[a1a2…a14],同理可得其他吊杆单独作用时的影响量，则该桥索力调整的影响矩阵为

A=[A1A2…An]T

该桥设计索力为[F],则得到受调向量

D=F-F0

(1)

x=A-1D

(2)

由联立公式(1)(2)可得吊杆张拉力x，将得到的吊杆张拉力按施工阶段施加在吊杆中，得到两次吊杆控制索力，如表1所示给出部分索力控制值。

表1 部分吊杆张拉控制索力 kN

在现场利用频谱分析法[11-12]进行索力测试，该法利用索力与拉索自振频率之间的关系获得索力。为防止拱肋支撑对吊杆索力产生影响，拱肋临时支撑在吊杆安装前即进行拆除。依据设定拟定的张拉顺序，两次张拉顺序均为由中间14号吊杆依次向两边张拉的顺序进行张拉，张拉力大小按表1索力进行施加，吊杆布置图如图6所示。进行索力监测时，除记录气温、临时荷载等影响因素，同时避免日照不均匀温度场的影响，选择日照较弱时间段进行索力监测，从而减小索力测试的误差，为索力施工控制的理论计算与预测提供准确的理论支持。

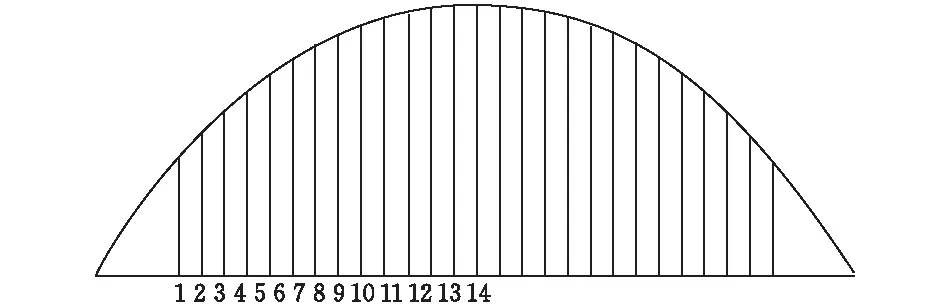
图6 吊杆布置

5 控制结果分析

这里选取成桥阶段的控制结果进行分析。

5.1 拱肋线形控制结果分析

选取拱肋1/8处、1/4处等关键截面进行线形测点布置，拱肋到成桥阶段累计位移的计算值与实测值进行对比分析如图7所示。

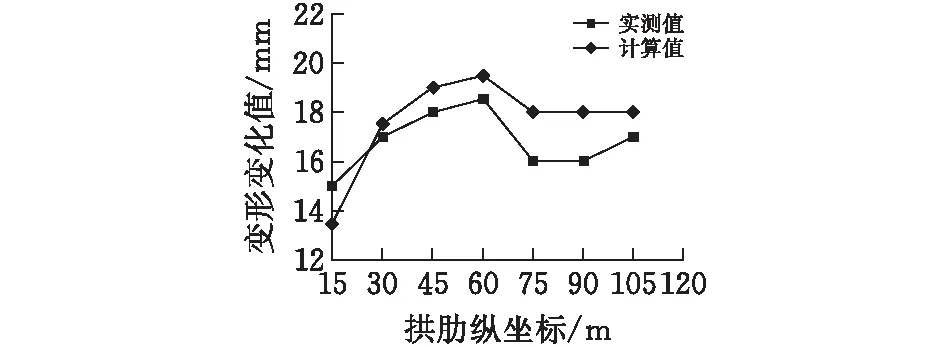
图7 拱肋竖向位移

由成桥拱肋竖向位移图可知，整个施工阶段拱肋拱顶处累计位移最大，有18 mm,拱肋整体位移变化趋势与有限元理论计算吻合良好，说明按二次抛物线进行预拱度分配所进行的线形控制取得了良好的效果，同时也验证了有限元计算边界条件设置与荷载布置符合工程实际。

5.2 拱肋应力控制结果分析

选取上游拱肋在成桥状态的应力进行分析，实测值与计算值对比分析如表2 所示。

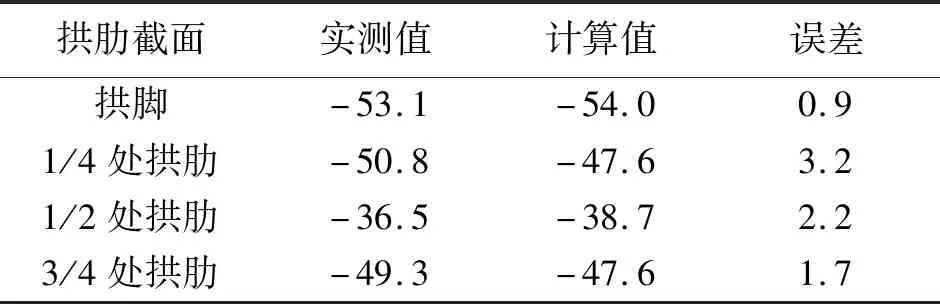
表2 上游拱肋应力监测结果 MPa

拱肋良好的应力状态是结构安全的重要保证，应力监控过程中，应力以拉为“+”，以压为“-”。由表2可知，在成桥后，拱肋最大应力不超过60 MPa,拱肋实测应力与计算值最大误差不超过5 MPa,说明拱桥受力状态合理。拱脚处压应力最大，最大压应力为53.1 MPa，远小于材料的容许应力，在合理范围内。

5.3 吊杆索力控制结果分析

对成桥后的吊杆索力实测索力值与计算值进行对比研究，如图8所示。

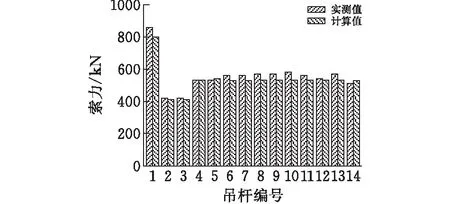
图8 吊杆索力对比

由图8对比分析可知，在成桥后的实测索力值与计算值的误差控制在10%以内，索力分布均匀，误差在设计允许的范围内。说明按照影响矩阵法所求得的吊杆张拉力进行张拉，桥梁结构最终的成桥状态符合满足设计要求。由于1号吊杆靠近拱脚，拱脚处刚度较大，导致1号吊杆索力值明显高于其它吊杆。吊杆索力实测值远小于钢材的抗拉强度，满足设计要求。1号吊杆设计值与实测值误差相对于其他吊杆误差较大，主要原因是拱脚处受力复杂，而模型主梁与横梁均使用梁单元模拟，参数设置较为简化，但误差仍在设计允许的范围内，可指导实际施工。