跨度128 m高速铁路系杆拱桥拱肋拟合预拱度研究

王振宇，刘世忠，谢兴定，白彦辉,杨少波

(1.兰州交通大学 甘肃省道路桥梁与地下工程重点实验室，甘肃 兰州 730070；2.中铁七局集团第二工程有限公司，辽宁 沈阳 110001)

桥梁结构须具备足够的竖向刚度、一定的横向刚度和匀顺的成桥线形[1]。拱肋预拱度设置是否良好是决定大跨度系杆拱桥成桥线形的主要因素[2]。在系杆拱桥的施工过程中及成桥后，拱肋由于受到很多因素影响，会发生弹性变形和非弹性变形[3]，这些因素将导致实际拱轴线发生变位，使最终的成桥拱轴线无法符合设计拱轴线要求[4]。因此在拱桥设计时，考虑设计拱轴线时还要设置施工预拱度。桥梁的恒载挠度一般由施工所设的反向预拱度克服[5]。

本文对高速铁路系杆拱桥有支架悬链线拱肋施工预拱度设置方法做出了系统介绍，在实际工程的基础上，结合理论分析，提出拱肋拟合预拱度的概念，弥补了规范中拱肋预拱度设置的部分空缺。

1 传统拱肋预拱度设置原理

最理想的拱轴线是与拱上各种荷载作用下的压力线相吻合，此时拱肋截面只受轴力，而无弯矩作用，从而能使材料的抗压性能得到充分发挥[6]。但当拱轴线与恒载压力线相吻合时，在活载作用下就不再吻合[7]。为使拱轴线符合设计要求，须在拱架上预留施工预拱度，以抵消各种影响因素产生的垂直变形[8]。

拱肋的拱顶是整个拱轴线挠度最大的区域，一般要考虑对拱顶设预拱度后，其轴线上的所有点都需要依据拱顶的预拱度来设置预拱度。2种常用预拱度设置方法如下[9]：

方法1。按拱脚推力影响线比例设置法，如图1所示，其中L为跨度。距拱顶x点的预拱度δx为

δx=δyx/y

(1)

式中,δ为设计提供的拱顶处施工预拱度。

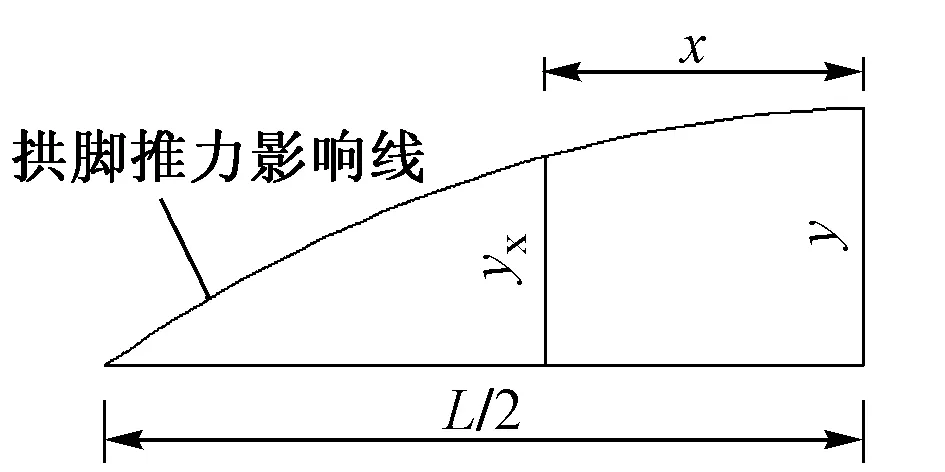
图1 推力影响线比例设置

方法2。对无支架或早期脱架施工的悬链线拱，裸拱肋的挠度曲线呈反M形，如图2所示，在考虑预拱度后的拱轴线放样坐标可按下式计算。

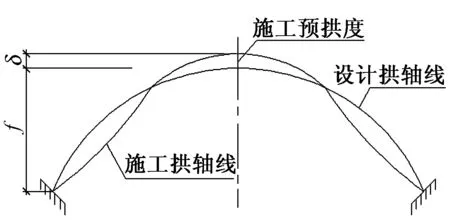
图2 反M形轴线设置

(2)

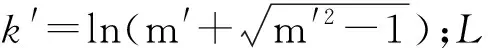
规范JTJ 022—85《公路砖石及混凝土桥涵设计规范》中关于预拱度的设置主要有2种方法，即上面提到的方法1和方法2(反M法);而规范JTG D61—2005《公路污工桥涵设计规范》中关于预拱度的设置只有方法1，将反M法及其相应的附录取消了。本文的拱肋为有支架悬链线拱肋施工，方法1及方法2都不能很好地满足规范要求，因而下文中提出了一种新的拟合预拱度设置方法。

2 拱肋拟合预拱度

2.1 拱肋施工拟合预拱度设置

本工程为一座主跨128 m的尼尔森体系钢管混凝土系杆拱桥，拱肋采用悬链线形，拱轴系数m=1.347，悬链线方程为

y=73.775 2(ch 0.810 68x/64-1)

(3)

系梁施工完成后在梁面搭设钢管支架安装拱肋。现取一半拱肋计算，以拱肋中心线与支座中心线交点为坐标原点，共分为9个控制点每节点相距8 m。

因本桥为悬链线形有支架施工拱肋，文献[10]根据规范反M形方法2与拱脚推力影响线方法1的对比结果可知，若按方法1设置预拱度后，其不再为悬链线形拱轴线。而方法2虽不适合大跨度拱桥拱肋有支架施工预拱度设置，但按其方法设置预拱度后仍为悬链线。若只改变拱轴系数其对应的拱轴线仍为悬链线。

鉴于此，综合考虑方法1与方法2的优点，本文提出一种新的预拱度设置方法，即先按方法1分配各控制点预拱度，再由方法2拟合新的悬链线。该方法的思路为：首先依据设计方提供的拱顶预拱度按拱脚水平推力影响线分配求得其他各控制点预拱度，然后以分配求得的L/4处和拱顶的设计预拱度为目标，通过拟合新的悬链线，求得新的拱轴系数m。

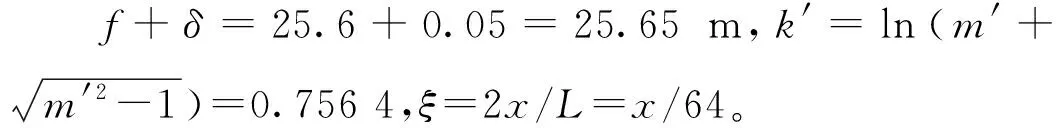
故拟合后含预拱度的修正悬链线放样坐标公式为

y′=85.5(ch0.756 4x/64-1)

(4)

分别用拱脚水平推力影响线分配公式(1)得出的9个拱肋控制点设计预拱度和用y′算出考虑预拱度的9个拱肋放样控制点坐标，并与公式(3)算出的拱肋设计坐标值y对比得出拟合预拱度，如表1所示。

新方法设置预拱度比较见图3。可知，m′=1.3拟合的新悬链线十分逼进设计预拱线形，由表1中数据发现最大误差只有0.002 m，分别出现在7L/32和11L/32及7L/16处。新方法得出的预拱度符合规范要求，且数值与设计方提供数值相符，数值十分逼进方法1计算结果且设计线形继承了方法2的优点，可见利用新方法计算有支架悬链线形拱肋施工预拱度是可行的。

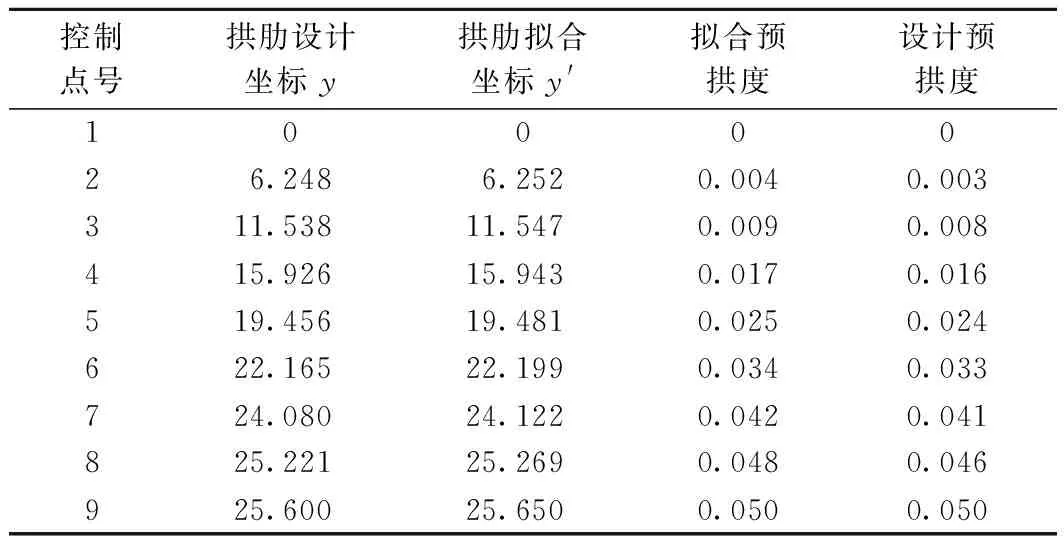
表1 新方法拱肋预拱度比较 m

图3 新方法设置预拱度比较

2.2 光电挠度仪现场监测拱肋施工

为高质量地完成拱肋施工且验证拟合预拱度的准确性，提出了运用桥梁光电挠度仪实时监测拱肋变形的措施。在监测过程中选取两拱肋拱顶处作为挠度变化关键截面进行观测。本桥拱肋混凝土分3次浇筑，依次是上弦管、下弦管和腹板，拱肋混凝土依次浇筑完毕拆除拱架且吊杆索力张拉后累计挠度见表2。

表2 吊杆索力张拉后拱肋累计挠度 m

由表2可知拱肋施工过程中由于拱肋承受自重、温度变化、混凝土收缩徐变、钢管拱弹性压缩，吊杆张拉等因素影响，累计挠度为0.04 m，小于施工实际拱顶预留拱度(0.05 m)。故光电挠度仪实时监测为拱肋施工提供了数字化保障，且验证了拟合预拱度的正确性。

2.3 建立全桥施工过程有限元仿真模型

为验证新方法公式(4)所得预拱度的准确性，运用大型桥梁有限元软件MIDAS/Civil建立全桥施工过程有限元仿真模型，模拟各施工阶段结构变位。在MIDAS/Civil中运用联合截面法成功地模拟了组合截面，使混凝土圆截面、腹板截面以及哑铃形钢截面在不同施工阶段逐步合成为符合实际的有效截面。建模过程中系梁和拱肋交接处采用局部刚域处理。

由于拱肋经过了空钢管搭设、混凝土灌注、混凝土收缩徐变、温度变化、拱肋支架拆除、吊杆张拉等施工过程，每一过程后必将有挠度积累，故拱肋挠度计算采用支架拆除吊杆张拉后的工况。计算结果表明：拱顶最大挠度为0.042 m，小于实际拱顶预拱度0.05 m，拱顶其他各点挠度均小于实际设置的预拱度。利用光电挠度仪现场实测的吊杆张拉工况下拱顶挠度值0.04 m，小于实际预拱度及计算挠度，故理论分析成果得到现场实测数据验证。考虑各种影响因素设置的预拱度符合现场实际，说明有限元模型的建立和边界条件的模拟符合工程实际，也验证了公式(4)所得预拱度的准确性，因而本文提出的新方法可适用于计算有支架悬链线形拱肋施工预拱度。

3 结论

本文以在建的高速铁路一座128 m尼尔森体系钢管混凝土系杆拱桥为工程实例。由于规范中对于有支架施工拱肋预拱度设置方法不够准确，因而本文提出了一种适用于有支架悬链线拱肋施工预拱度设置的新方法，即依据设计方提供的拱顶预拱度按拱脚水平推力影响线分配求得其他各控制点预拱度，然后以分配求得的L/4处预拱度和拱顶预拱度为目标，拟合新的悬链线求得新的拱轴系数，用新的悬链线方程求出各控制点预拱度，该方法既保证了数值的准确性又保证其线形仍为悬链线。利用光电挠度仪进行现场监测得出拱肋施工实际挠度，结果表明其值符合规范要求且与设计方所提供数值相符，最后通过建立符合实际的施工过程有限元仿真模型得出吊杆张拉后L/2拱肋各控制点考虑了各种影响因素的挠度，进一步验证了新的拟合预拱度设置方法。本文提出的拟合预拱度设置方法预拱度的设置且符合现场实际，为该桥高质量的建成，起到了关键性的技术保障作用。