小波变换在钢丝绳漏磁检测中的应用

银鸿　文轩　杨生胜　王鹢　李存惠　王俊

摘要：针对钢丝绳漏磁检测中信号易受自身股波及环境噪声干扰的问题，采用傅里叶变换和小波变换对缺陷漏磁检测试验数据进行了研究。简述了钢丝绳漏磁检测法的基本原理及试验过程，利用傅里叶变换对试验数据进行了幅频特性分析，并用低通滤波技术进行了信号处理;同时，从小波变换原理出发选取了最优小波基对原试验数据滤波处理。结果表明，相较与傅里叶变换滤波技术，小波变换滤波在钢丝绳漏磁信号处理中更具优越性，能更好地消除干扰噪声，为后续的钢丝绳缺陷成像化检测和定量化检测应用提供支持。

关键词：钢丝绳;无损检测;漏磁检测;傅里叶变换;小波变换

中图分类号：Q441;TG806  文献标识码：A

1 引 言

钢丝绳作为提升、运输和承受设备重量的关键挠性构件，在直升机运输、航母舰载机降落阻拦等重要军事应用领域以及矿产、旅游、建筑等民用行业中扮演着重要的角色[1，2]。长时间的载重、拉伸、扭曲等的工作及恶劣使用环境的影响，会使钢丝绳出现磨损、疲劳、腐蚀甚至断裂的问题，依靠先进的无损检测手段可有效排查断绳事故隐患，并合理评估钢丝绳在用寿命，其经济和社会效益都是可观的[3]。

漏磁检测法是目前检测钢丝绳缺陷较为适宜的方法，可对钢丝绳内外部断丝及其横截面积损伤实现检测。但由于钢丝绳本身表面存在周期性变化的股波，且检测环境本底磁场复杂多变、检测电路本身的电磁噪声干扰、检测过程中抖动干扰等因素往往影响着漏磁信号的准确判断。针对该问题，常采用信号处理方法削弱信号中的多余内容，滤出混杂的噪声和干扰，将信号转换为易于识别，分辨的形式。本文采用傅里叶变换和小波变换对试验得到的钢丝绳漏磁信号进行了分析研究。首先对信号开展傅里叶变换，分析其频谱、功率特性，并通过滤波对信号结果进行讨论;然后，利用小波变换方法对同一信号进行小波变换，选取小波基，对信号进行多层分解，不同频段阈值消噪声，重构，实现信号的小波变换处理，对处理结果进行讨论;最后，将傅里叶变换与小波变换降噪后的结果进行了对比分析，验证小波变换方法在信号处理中的实用性及其优越性，提升钢丝绳缺陷检测的准确性和有效性，为后续的钢丝绳缺陷成像化检测和定量化检测应用提供支持。

2 钢丝绳缺陷漏磁检测原理及检测试验

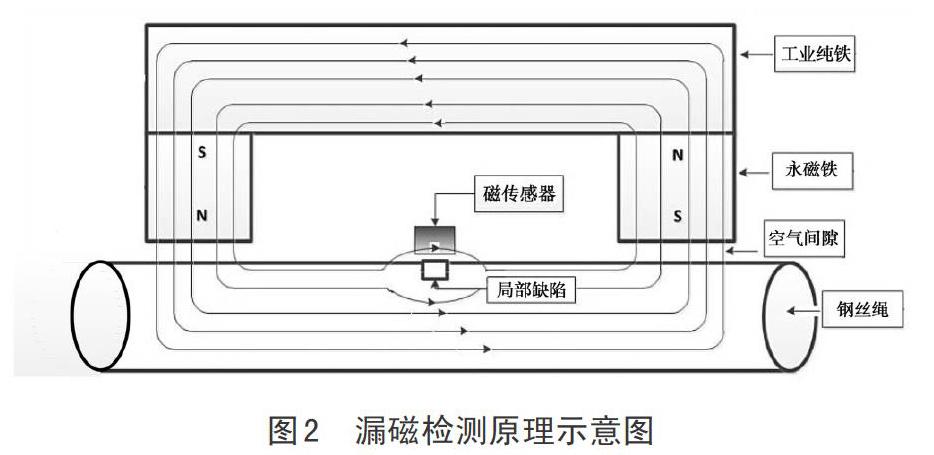
钢丝绳主要成分是高质量的碳素钢，有较好的导磁性，利用永磁体对其进行励磁，并与永磁体、轭铁、空气气隙形成励磁回路，使钢丝绳达到轴向局部励磁饱和（图1）。当无缺陷时，钢丝绳内磁通量无变化;当出现断丝，其磁通量显著减小，泄露于空气中成漏磁场，通过磁传感器检测漏磁场即可实现缺陷的定位或定量检测。

利用励磁装置和磁传感器组成检测探头模块，利用NI-LabVIEW组成数据采集和处理模块，对存在缺陷的钢丝绳样件进行检测，通过获得信号的幅值变化实现缺陷深度和缺陷大小的评判。选择探头提离距离为3mm，测量方向为轴向测量方向，分别对点击并拖拽以移动8mm和点击并拖拽以移动16mm直径的含缺陷钢丝绳进行检测，其结果如图3，4所示：

点击并拖拽以移动图3点击并拖拽以移动8mm的损伤钢丝绳检测结果

点击并拖拽以移动图4点击并拖拽以移动16mm的损伤钢丝绳检测结果

由图3、图4可见，钢丝绳缺陷处的检测信号电压幅值发生会突变，可以通过提取信号幅值大小和产生幅值的采样时间等特征值来实现缺陷存在与否、缺陷具体位置，缺陷大小的评判。干扰噪声造成的信号毛刺明显，影响缺陷幅值的判断，尤其易使小缺陷波形淹没在噪声信号中，造成漏检和误检，

3 基于傅里叶变换的缺陷信号处理

传统的信号分析是建立在傅里叶变换的基础之上的，傅里叶变换是频谱理论的基础。对于一维的信号f（t）来说，其连续的傅里叶变换定义为：

点击并拖拽以移动            （1）

对于参数点击并拖拽以移动的任何实数值都存在，则称点击并拖拽以移动为点击并拖拽以移动的傅里叶变换。函数点击并拖拽以移动一般为复数，可以写成：

点击并拖拽以移动   （2）

其中，点击并拖拽以移动称为点击并拖拽以移动的傅里叶谱，点击并拖拽以移动为相位谱，点击并拖拽以移动为能量谱。

可通过傅里叶变换，将时域的信号转化为频域信号，这在信号分析和处理方面具有非常大的优势。对试验测得的两组数据进行傅里叶变换分析，图3，4中8mm和13mm损伤钢丝绳信号的频谱特性如图5，6所示，可见，不同直径规格的损伤钢丝绳的缺陷信号虽在时域表现形式不同，但在频域上频率分布范围一致，且缺陷信号的频率较低，主要集中在0～0.03Hz间。因此，可利用低通滤波器对信号进行滤波处理。处理后的信号与原始信号相比有很好的一致性，信号中的环境噪声等外界因素造成的影响基本被滤掉，信号变得很平滑（图7-8）。

4 基于小波变换的缺陷信号处理

小波分析是将信号与小波函数进行卷积，把信号分解成不同频段和时段成分，是一种变分辨率的时频分析方法。在分析低频信号时，其时间窗很大;而分析高频信号时，其时间窗较小。这恰恰符合实际问题中高频信号持续时间短，低频信号持续时间长的自然规律，因而被誉为“数学显微镜”[4]。

设点击并拖拽以移动，其傅里叶变换为点击并拖拽以移动，当点击并拖拽以移动满足完全重构条件或者恒等分辨率条件时：

点击并拖拽以移动          （3）

此时称点击并拖拽以移动为一个母小波或基本小波。将母函数点击并拖拽以移动经伸缩和平移后得到：

点击并拖拽以移动      （4）

称其为一个小波序列。其中：点击并拖拽以移动为伸缩因子，点击并拖拽以移动为平移因子。对于任意的函数点击并拖拽以移動的连续小波变换为：

點击并拖拽以移动   （5）

其重构公式（逆变换）为：

点击并拖拽以移动    （6）

Donoho提出的基于阈值小波去噪法[53-54]，按下图所示的处理过程，实现钢丝绳断丝检测信号的降噪处理。

小波变换对钢丝绳断丝信号的降噪具体算法：

根据钢丝绳的断丝信号，选取出相应的小波函数，对试验得到的信号进行小波分解。

对各尺度的小波系数选定合适的阈值T，对各频段内与断丝信号无关的数据进行降噪滤波处理。

对经过阈值函数处理降噪后的小波系数进行钢丝绳断丝信号重构，得到去噪重构后与钢丝绳实际断丝信号对应的逼近信号。

（1）  小波基的选择

最优小波基的选择是小波变换的一个关键点。根据信号处理的不同目的，以及具体应用情况，经验性地选取一些小波[5，6]，然后对试验信号进行处理，通过处理结果与处理期望得到的结果相对比，最终得到最优小波基。

对于钢丝绳断丝信号小波基的选择，必须要求小波基具有线性相位和紧支撑性。常用的紧支撑性小波基函数只有Harr、Daubechlies、Biorthgornal、Coiflets、Symlets五个小波。而钢丝绳信号处理中最为常用的是Harr和DB小波基[7，8];如图9所示，分别选用了Harr和Db1、4、10小波基进行了6层分解，从图中能够明显看出，Harr和Db1小波变换后，低频信号连续性不好，信号呈现出方波形式，与钢丝绳实际损伤后的特征信号不符。相比之下，Db4小波基变换后的低频信号与Db10变换后的低频信号相比较，Db4小波基变换后的低频信号信号未损伤部位更加平滑，且四个损伤位置都得到了很好的表示，因此Db4小波基最适合钢丝绳的断丝特征信号。

（2）小波分析在钢丝绳无损检测中的应用

小波分析具有良好的去噪效果，通过小波分解后，所得到的低频系数主要反应信号的信息[9]。对8mm损伤存在损伤的缺陷检测波形进行小波变换分析，利用Db4对其进行了6层分析和重构，具体分解过程如图10左上所示，信号（0，0）被分解为低频部分（1，0）和高频部分（1，1），之后再对低频信号（1，0）进行分解，从上到下，依次分解至6层。图10左下为信号分解1层时的高频信号（1，1），右上为6层分解后的低频信号（6，0），通过逐层低频信号的滤波、重构，进而实现实现钢丝绳断丝信号的处理。

点击并拖拽以移动

利用Db4小波基对钢丝绳缺陷试验数据（图3，图4）进行了分解滤波和重构，结果表明，漏磁信号在很大程度上得到了优化（图11、图12）。

点击并拖拽以移动

点击并拖拽以移动

5 缺陷检测信号的不同处理方法结果对比

图7、图8为试验数据经过0.3Hz低通滤波器滤波的信号，图11、图12为试验数据经过小波变换后的信号图像，从总体上可看出，经过傅里叶变换、滤波后的曲线变得平滑，这种结果与所用传感器本身的超高信噪比有着直接的关系，因此，通过滤波处理后，信号整体的变化不大，经过小波变换后信号的整体曲线变得平滑，许多未损伤部位的小范围波动被抹平，这是由于小波变换将信号在按照不同的频段进行分解，将每个频段的信号进行滤波处理，最后再将滤波后的信号进行重构，这使得判断结果更加明显，信号处理方法更加科学;此外，从细节上，损伤部位缺陷的特征信号并没有减小，这在很大程度上提高了缺陷检测结果的信噪比;如果钢丝绳样件检测速度恒定时，小波变换能够最大限度的消除掉钢丝绳的股波信号。

因此，小波变换相比与直接低通滤波在钢丝绳无损检测中更具有优势，可作为钢丝绳定量检测的一种重要数据处理方法。

6 小结

本文针对钢丝绳缺陷漏磁检测信号因受干扰噪声影响而难以准确判断的问题，提出了利用傅里叶变换和小波变换对对缺陷漏磁检测试验数据进行研究，通过傅里叶变换得出不同直径钢丝绳缺陷信号在时域表现不同，但频率分布范围一致，其频带范围为0～0.03Hz，并利用低通滤波技术得到较为平滑的信号结果;同时，从小波变换原理出发，选取最优小波基对原信号阈值滤波处理，结果表明小波变换在钢丝绳无损检测技术中较传统的傅里叶变换滤波技术具有更好的适宜性，能更大程度消去干扰噪声信号，保留有用缺陷信号特征，从而提高缺陷检测准确度，在后续的钢丝绳缺陷定量化及成像化检测中具有较好的应用潜力。

参考文献

[1] 王桂林 浅析航空母舰阻拦索及其改进方法[J] 黑龙江科技信息，2013，（11）：65-66

[2] 陶德馨，艾丽斯佳. 基于弱磁探伤的钢丝绳无损检测技术[J]. 中国工程机械学报，2009，7（1）：96-99.

[3] The University of Reading. Wire Rope Non-Destructive Testing - Survey of Instrument Manufacturers[R]. London： Health and Safety Executive， Offshore Technology Report - OTO 2000 064. 2000.

[4] J.Rafiee，P.W.Tse，A.Harifi et al.A novel technique for selecting mother wavelet function using an intelligent fault diagnosis system Expert System with Applications[J]，2009，36（3）：4862-4875.

[5] 欧阳鑫玉，唐跃鹏.基于小波变换的奇异性检测在信号分析中的应用[J].鞍山科技大学学报，2006，29（3）：250-255.

[6] 陈希平.基于MATLAB的奇异信号检测中小波基选择研究[J].计算机仿真，2004，21（11）：48-50.

[7] Jian-Da Wu，Chiu-Hong Liu.An expert system for fault Diagnosis in internal combustion engines using wavelet packet transform and neural network[J].Expert Systems with Applications，2009，36（3）：4278-4286.

[8] N.Ahuja，S.Lertrattanapanich，N.K.Bose.Poperties determining choice of mother wavelet[J].IEE Proc.Image Signal Process，2005，152（5）：659-664.

[9] MANGANIELLO L，VEGA C，RIOS A，et a1.Use of wavelet transform to enhance piezoelectric signals for analytical purposes[J].Analytica Chimica Acta 2002，456：93-103.