初中生数学解题后反思品质研究

黄华娟

摘 要 初中生数学解题后及时进行反思学习，能够加深学生对数学知识的理解和认知，促使学生养成良好的反思品质。因此，本文结合初中数学有关内容，对初中生数学解题后反思品质的培养展开研究，从而引导学生养成良好的数学解题后反思的习惯。

关键词 初中數学;反思品质;解题;研究

中图分类号：A715 文献标识码：A 文章编号：1002-7661（2020）27-0132-02

数学是初中阶段的重点科目，而解题又是学习数学知识的核心。所以，学生应该了解和掌握解决问题的步骤及方式，才能高效地解决数学问题。其中，数学解题后的反思是解题过程中的重要阶段，也是学生深化和提高自身解题思维的重要途径。因此，如何培养学生数学解题后的反思品质，是当前数学教师应该重点思考和研究的课题。

一、反思数学解题中的知识点，构建有序、完整的认知体系

初中生解答数学问题，必须具备良好的数学知识基础，才能在大脑中检索和提取与数学题目有关的知识点，从而快速地找到问题的解答思路。但是，如果学生大脑存储的数学知识是零散的、无序的，会影响到学生应用数学知识解答问题的效率。因此，在初中数学解题中，教师应该重视学生解题后反思品质的培养，从而在反思过程中，帮助学生整合所学的数学知识，进而逐步建立起有序、完整的数学认知体系，这样学生在解题过程中就能快速、精准地找到解题所涉及的知识点。其中，教师可以先引导学生对已做题目进行分类，再找寻题目中涉及到的知识点，并理解题目中知识间的关系，从而对知识进行整合，以形成有序、完整的认知体系，进而养成良好的解题后反思品质。

以下面这道初中数学二次函数题目为例：已知二次函数为y=x2-x+m

（1）写出它的图像开口方向，对称轴及其顶点坐标;

（2）m为何值时，顶点在x轴上方;

（3）若抛物线与y轴交于A，过A做AB∥x轴交抛物线于另一点B，当S△AOB=4时，求此二次函数解析式。

分析：针对问题（1），学生可以用配方法求出二次函数的对称轴及其顶点坐标，同时题目给出的二次函数解析式，可以直接判断出函数的开口方向。

针对问题（2）中顶点在x轴的上方，那么顶点的纵坐标应该为正，即顶点的纵坐标大于0，这样就可以得到4m-1/4>0，继而求出m>1/4。针对问题（3），AB∥x轴，那么A、B两点的纵坐标应该是相等的，这样我们就能求出m的值。

反思：这道题目的解答涉及到多个知识点，而且知识链也比较长，学生需要正确理解和掌握二次函数常数a，b，c的符号与二次函数性质及其位置之间的关系，才能快速地找到解题的突破口。因此，在解题后，学生需要经常加强二次函数知识点的训练和反思，从而构建完整的二次函数图像、性质、表达式等知识体系，进而在大脑中建立起有序、完整的网络知识架构，这样才能增强知识的可用性，最终快速、准确的解题。

二、反思数学解题的过程，锻炼学生的独立反思能力

在以往解题过程中，很多学生过于重视解题的答案，忽略了解题过程中的反思，这样不利于学生发现自身解题中存在的问题，进而学生无法对自己的问题进行及时地改正。因此，在初中数学解题过程中，教师仍需加强学生反思数学解题过程，以培养学生独立分析和批判的数学思维，促使学生养成良好的反思习惯。在反思数学解题过程中，教师应该根据学生解题实际情况，引用一些具有迷惑性的数学问题，并给予学生一定的思考和探索时间，让学生独立思考和分析问题。然后，引导学生作出解题后的反思，促使学生通过反思来弥补自身存在的不足和思维缺陷。

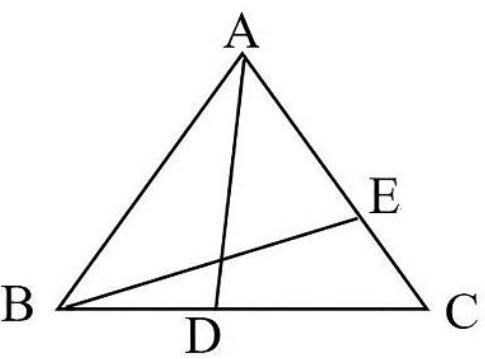
以下面这道初中数学“三角形”问题为例：如图，在三角形ABC中，AD平分∠BAC，BE是高，∠BAC=600，∠EBC=200，求∠ADC的度数。

分析：学生需要明确所求的角属于哪一个三角形的内角或者外角，然后分析出题目中存在哪些等量关系，并列出相关的方程等式，最后通过解方程就能得出相关的答案。

反思：在解答类似的三角形数学题目时，教师应该引导学生做出解题后的反思学习，让学生独立去寻找、分析题目中的条件，从而锻炼学生的独立思考能力，促使其在反思中发觉自己存在哪些解题思维上的缺陷，进而引导学生看清自身存在的不足，最终促使学生养成严谨、批判的解题思维品质。

三、反思解题中存在的规律，引导学生寻求最佳的解题方法

解答数学问题的方法有很多种，学生需要懂得反思题目中存在的规律，分析题目是否可以采取另一种方法进行解答，促使学生学会变通解题的路径，从而找到最佳的解题方法。那么在解题过程中，教师可以融入激励教育理念，通过语言上的鼓励，激励学生重新思考和检查题目的结果，从而让学生多角度去观察和联想，以寻求出最佳的解题方式，进而锻炼学生的大脑思维。同时，教师也可以组织学生展开合作学习，引导学生互相合作、探讨自己的解题方法，促使学生与他人交流中产生新的解题思路。

以下面这道解方程问题为例：1/（2x2-3）-8x2+12=0

分析：在这道方程问题中，很多学生会按照一般解分式方程的方法进行问题的解答，通过去分母之后，可以出现x的4此方程。对于初中生而言，要计算4次方程是很有难度的，也很容易出现计算错误。这就需要学生学会观察和分析，以寻找题目中方程的规律。其中，学生可以观察-8x2+12和2x2-3之间的关系，就可以立即想到使用换元法进行解方程，从而设y=2x2-3，将原方程化为：1/y-4y=0，最终简化计算过程。

反思：可见，在解题之后，教师引导学生进行反思学习具有一定的意义和作用，它能够让学生反思此题中有没有其它的解题方法，从而引导学生观察题目中的规律，促使学生学会进行解题后的反思学习，进而把题目中存在的某种内在联系进行深入地挖掘，最终寻求出通往成功解题的途径。因此，教师应该抽取课堂部分的教学时间，让学生有机会展开反思学习，互相分析自己的解题方法，以激发学生的解题思维。

四、结语

综上所述，初中数学教学不只是单纯传授课本中的知识，更重要的是引导学生做好课后的反思学习，促使学生养成良好的反思品质，这样学生才能真正领会数学知识之间的关系，进而加深学生对数学知识的理解和认知。因此，在初中数学解题教学中，教师应该从多方面、多角度培养学生的反思品质，使其意识到反思学习的重要性，进而养成良好的反思学习习惯，最终从反思学习中提升自身的观察、分析以及总结能力。

参考文献：

[1]汤景党.初中数学教学中学生解题能力的培养[J].数理化解题研究，2016，2（32）：25-25.

[2]苏仕亮.初中数学解题教学中学生思维品质的培养[J].数理化解题研究，2016，16（32）：326-326.