U形无铁心永磁直线发电机简化建模方法研究

邱书恒，张 杰，孙贤备，张 驰，康 鹏

(1.中国科学院宁波材料技术与工程研究所，宁波 315201；2.宁波菲仕运动控制技术股份有限公司，宁波 315803)

0 引 言

随着经济和社会的不断发展，能源需求也日益增长。现阶段，人类所使用的能量主要来自于化石能源，据统计，截至2016年底，全球最终总能耗的79.5%来自煤、石油、天然气等化石燃料[1]。化石燃料在其燃烧和使用过程中暴露出一系列问题，譬如资源短缺、温室效应、环境污染和地质生态破坏等[2-4]。开发和利用新型可再生能源成为破解上述矛盾的关键。海洋覆盖了地球 71%的表面，其中蕴藏着无穷无尽的能量。波浪捕能技术旨在将海洋波浪所蕴含的动能或势能转换为电能加以利用。前人总结出了多种不同的波浪能提取途径[5]，目前为止，相关的专利与新技术已有数千个。但总体来说，运动转换的途径不外乎两种：其一是将直线往复运动转换为旋转运动驱动旋转发电机发电；其二是采用直线发电机，直接利用波浪能的直线往复运动驱动。

在波浪能的开发与利用中，英国爱丁堡大学的Neil Hodgins等采用了一种U形无铁心永磁直线发电机,次级运动速度为1.5 m/s时，线电压峰值为279 V，平均输出功率10.4 kW，效率约70%[6]。Rieghard Vermaak等提出了一种无铁心直线发电机结构，将U形次级进行圆周布置，其磁路呈圆环形，相较传统电机，该结构可以减重16%，有效提高了材料的利用率[7]。但随之而来的问题是，该结构复杂度较高，对加工和装配的要求也较大提高。

本文针对双边开口长次级U形无铁心永磁直线发电机(以下简称UCL-PMLG)进行研究，其结构如图1所示，电机次级截面如字母“U”，U形铁心内侧表贴两列面对面布置的磁钢，每块磁钢与对面相邻的磁钢充磁方向相同，与相邻的磁钢充磁方向相反。在此前，这类无铁心结构的直线电机由于其高控制精度的优点往往被用于精密直线驱动场合，如加工车床、纺织车床等[8-9]。而将无铁心结构的直线电机应用于波浪能发电场合时，也有不少优点：1)当无铁心初级作为动子时，其惯性较小，使得电机可以具有更高的加速度和减速度；2)电机次级中没有导磁材料，也不会存在由于齿槽配合带来的齿槽力和纵向边端效应带来的定位力，可以降低起动推力，但存在低速特性较差、漏磁、效率低、装配困难等缺点。本文针对无铁心永磁电机开展了物理建模、有限元分析和实验研究，提出了一种更为简化的物理模型，并推导了一种变速运动下快速求解波形的映射变换方法，最后通过实验验证了建模分析的准确性。

1 发电机物理模型

为了建立直线发电机的磁场理论分析模型，需要做出如下假设：

1)忽略z轴方向的磁场变化及纵向端部效应，因此各电流方向仅存在z向；

2)假设磁钢永磁体被均匀磁化，磁体内的各点磁势大小及方向都相同；

3)假设发电机各部分在纵向(x方向)无限长，永磁体横向(y方向)磁化；

4)磁钢磁导率、初级绕组与气隙磁导率均等于空气磁导率，且各个方向均匀同性，即μm=μCu=μag=μ0；

5)除绕组外，其他部件的电导率为0；

6)铁磁材料未饱和，即假设背铁磁导率无穷大，μi=∞，且各向均匀同性。

基于以上假设，可以将无铁心永磁直线发电机的物理模型简化在一对极内，如图2所示。

图2 U形无铁心永磁直线发电机简化模型

1.1 次级永磁体等效电流密度

根据永磁体的排布方式，可认为其等效磁势呈方波分布，其傅里叶级数形式如下[10]:

(1)

而永磁体等效电流密度可以用式(2)求得[11]:

(2)

式中：

(3)

式中：Br为永磁体剩磁；M0为永磁体磁化强度；lm为永磁体长度；μ0为空气磁导率。

1.2 永磁体单独作用下磁场解析

当永磁体单独作用时，可将求解区域划分为三个分层，分别为绕组区域、磁钢区域和背铁区域，如表3所示。

由于假设电机除了绕组外其他部分电导率为0，且磁场强度H和磁通密度B之间存在本构关系B=μH，那么根据麦克斯韦方程组的微分形式可知，磁场的矢量磁位方程可通过式(4)表示[12]：

×H=×(×A)=J

(4)

那么在图 3的Ⅰ′,Ⅰ,Ⅲ区域无电流密度，应满足式(5):

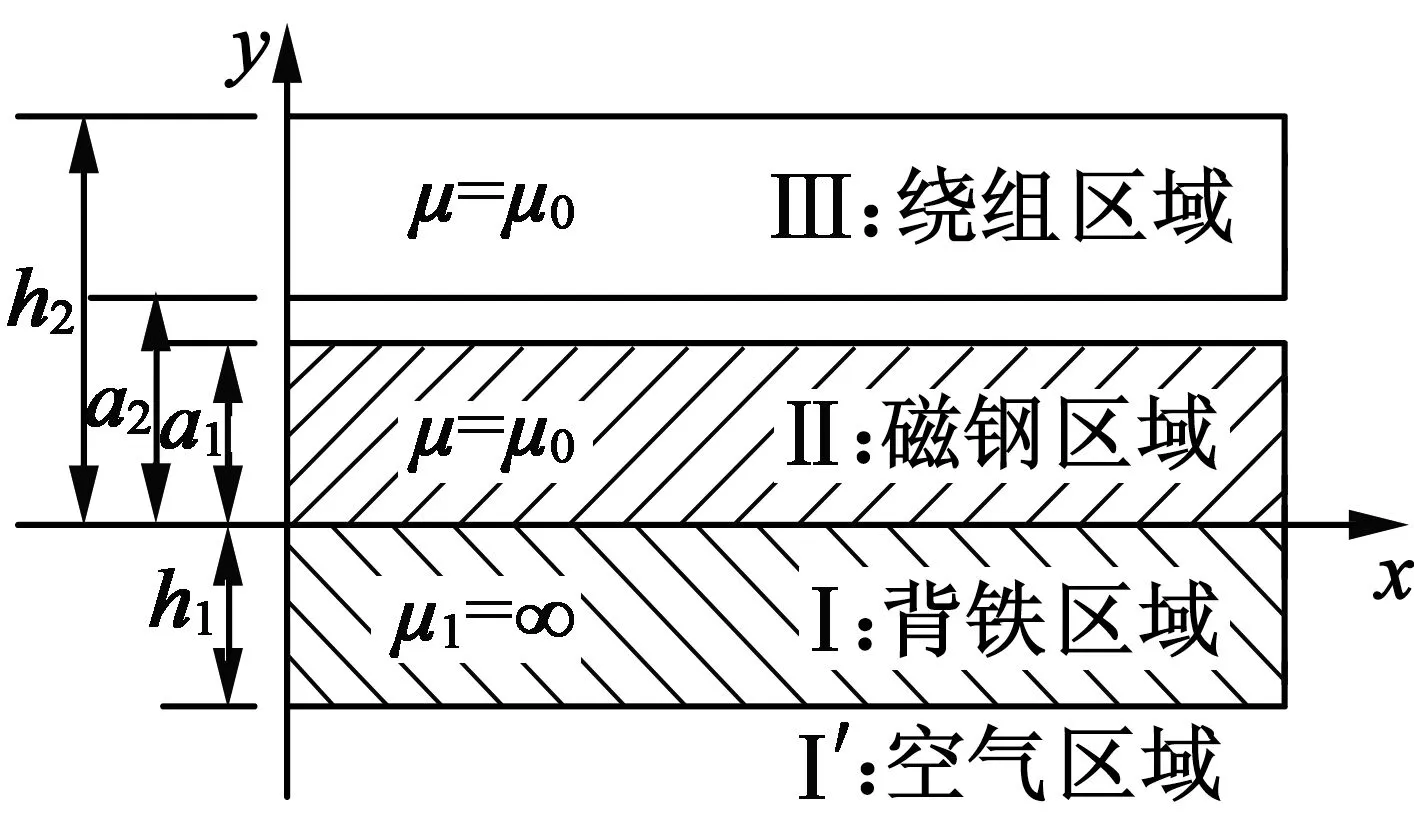
图3 永磁体励磁磁场分析分层线性模型

(5)

而Ⅱ区域为有等效电流密度区域，应满足式(6)：

(6)

当y=-时，有AⅠ′=0；在区域Ⅰ下方边界上，即当y=-h1时，应满足关系AⅠ′=AⅠ和在区域Ⅰ和Ⅱ交界处，即当y=0时，应满足关系AⅠ=AⅡ和在区域Ⅱ和Ⅲ交界处，即当y=a1时，应满足AⅡ=AⅢ和区域Ⅲ的上边界为镜像线，那么当y=h2时，应满足Neumann边界条件，即将这些边界条件代入偏微分方程的通解后，可联立得一组线性方程组，求解该线性方程组可求得各区矢量磁位如下式：

(7)

(8)

(9)

引入Tn,n=1～5，来简化公式，Tn的表达式如下：

(10)

(11)

(12)

(13)

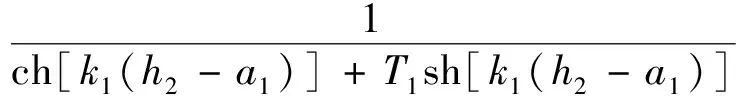
(14)

在求矢量磁位后，可根据泊松方程可推导出不同位置的磁密方程[10]：

(15)

式中：i=Ⅰ，Ⅱ，Ⅲ；Bix为磁密x分量；Biy为磁密y分量；Bi为磁密绝对值。

1.3 空载电动势方程

与绕组交链的磁通可以通过对y向磁密进行面积分求得：

(16)

式中:N为绕组匝数；hm为磁钢z向高度。为简化公式，引入T=T1T5。

当初级以速度v运动时，绕组交链的时变磁通方程可以用式(17)表示，而空载电动势是时变磁通对时间的偏导，化简后如式(18)所示。

Ψ(t)=kWΨ0sin(2πvt)

(17)

(18)

式中：kW为绕组系数；fe为电机电频率。

2 发电机亚正弦运动状态下的特性调整

当初级以速度v做匀速运动时，其绕组交链的磁通量也按正弦规律变化。不难发现，磁通变化的频率，也就是电机的电周期，即一相轴线N或S极轴线重合时起，运动到下一个N或S极轴线为止所需要的时间，可以用下式表示。

而电机的电频率即：

(19)

因此，当初级做匀速运动时，发电机端电压：

(20)

式中：i=1,2,3,分别表示U，V，W三相；ΨP为电枢绕组和永磁体共同作用下的合成磁通。

此时，三相直线发电机端电压与三相旋转发电机端电压无异，为三相相位相差120°的定频定幅正弦波，如图4所示。

图4 匀速运动下直线电机端电压波形

而当发电机初级处于变速运动时，机端电压的幅值和频率都是时变的，改写式(20)可得亚正弦状态下的电压方程：

(21)

而通过数值解法求得结果为在时间上离散化的一组矢量，而无法利用解析式表达；而直接在数值解法中引入时变的速度v(t)又会大大降低求解效率。那么寻找一种从匀速运动到亚正弦运动的映射关系，如图5所示，可以较好地解决这个问题。

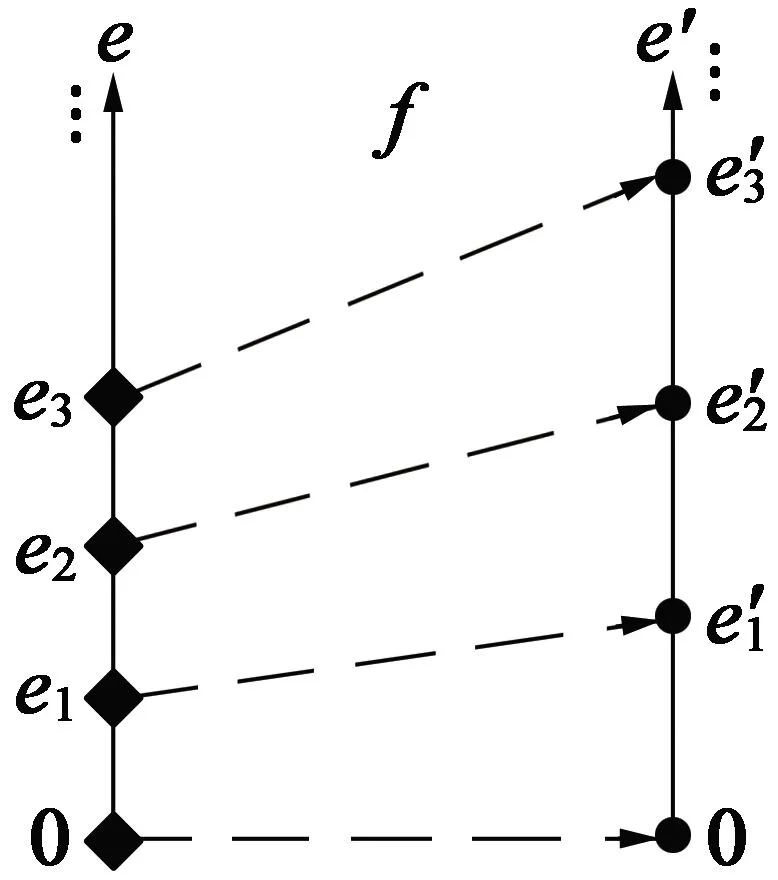
(a)y轴映射关系

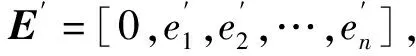
(22)

即：

(23)

(24)

即:

(25)

通过上述映射关系，可以使得在求解模型时只计算一个匀速运动周期的结果就可以推广到整个变速过程中去，并且无论变速运动的形式如何，都可进行推广，因此，可以大大减少模型求解所耗费的时间。

3 发电机有限元模型简化及仿真

有限元方法是一种求解微分方程数值解的数值技术，被广泛利用于求解Maxwell方程组，在电机电磁场分析领域常用的商业软件有JMAG，Ansys Maxwell，Magnet等。

根据上文的分析可知，U形无铁心永磁直线发电机可以被简化为一种最小周期镜像二维模型，如图6所示，模型总长仅为一倍极距，滑移面上侧为运动的初级部分，滑移面下侧为静止的次级部分，简化后该模型网格总量仅为732个即可精确求解出磁场分布。物理模型的尺寸参数及材料特性在表1中给出。

表1 U形无铁心永磁直线发电机参数

图6 最简模型及边界条件

模型中的对称边界，应满足第二类边界条件。由于电机沿对称边界上下对称，所以磁矢势A在该边界上下的分布也对称，而由于A在所有位置都是连续的，那么A在对称边界上x方向的偏导为0。第二类边界条件描述了在该边界上，磁场强度H的切向分量和磁通密度B的法向分量保持连续[14-15]。模型中的周期性边界属于反对称周期边界，若以模型右侧边界为源边界，左侧边界为目标边界，那么源和目标边界上的场值符号相反[16]。电机绕组采用叠放方式，学者马振琦等人论证了叠放绕组能产生比非叠放绕组更大的电磁推力[17]，而考虑到气隙内空间有限，将绕组分层8组，每组46匝，最后引出线串联连接。在本模型中，对绕组简化为仅建立单边导线束模型。

首先,对所建立的电机模型进行静磁场分析，磁密云图结果如图7所示。图7中也绘出了磁力线，即等磁势线，可见磁力线垂直对称边界穿过。

图7 U形无铁心永磁直线发电机磁密云图

取水平线y=14.2,13.2,12.2,11.2,10.2,9.2mm为观察位置，并绘制磁密y分量曲线与解析计算值进行比较，如图8所示，其中y=10.2,9.2 mm位置在上文的分析中属于区域Ⅱ，其他部分属于区域Ⅲ，y=14.2mm位置为气隙中心位置磁密曲线。

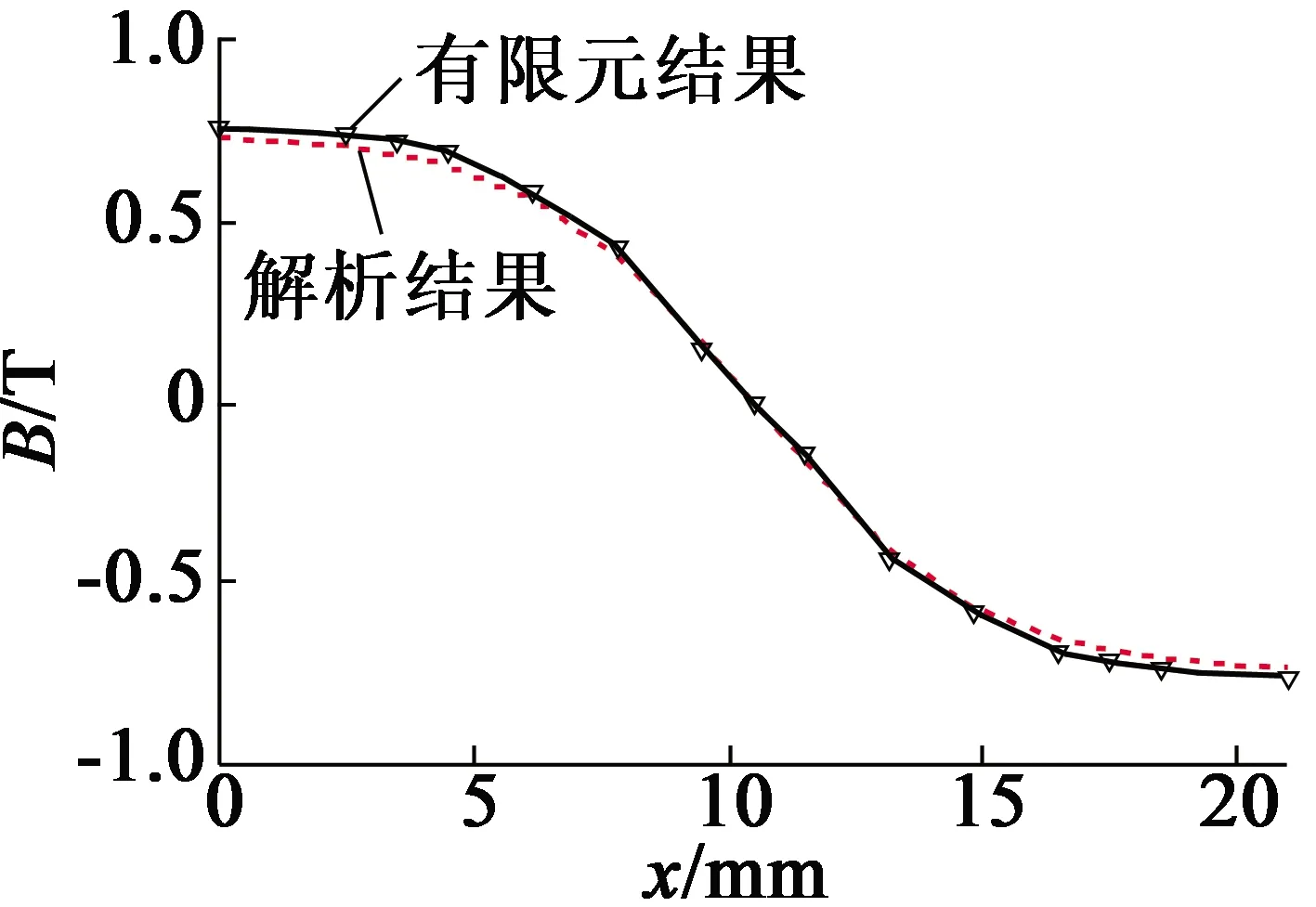
(a)y=14.2 mm

由于模型简化后宽度仅为一个极距，绘制的磁密曲线仅有半个周期，从图8中可见，各个位置的磁密沿x轴呈现奇函数分布，复合解析公式结果，同时解析解法求得的结果在接近气隙中心时略小于有限元结果，而在接近磁钢处略大于有限元结果，这是由于在进行解析求解时，仅计算了基波、3次和5次谐波，若仅对比基波幅值，解析结果比有限元结果均略小，其差距在5%以内。而在气隙中心线位置，磁密波形更接近正弦波，如图9所示，y=14.2 mm和13.2 mm时，高次谐波对计算结果较小，因此出现解析结果峰值比有限元峰值略小的情况。图8特定位置磁密空间波形结果与对比如图8(a)，图8(b)所示；而随着求解位置接近磁钢，由于表贴磁钢的凸极性，磁密波形更接近方波，如图9所示，y=12.2 mm和11.2 mm时，高次谐波对计算结果影响增大，这使得磁密波形趋于矮胖，从而使得未计及高次谐波的解析结果峰值比有限元结果略高，如图8(c)，图8(d)所示。在分析区域Ⅱ(磁钢区域)内的磁场时，将高次谐波(7次、9次)也考虑进去，所以，在图8(e)，图8(f)中，解析结果峰值与有限元结果更为接近。

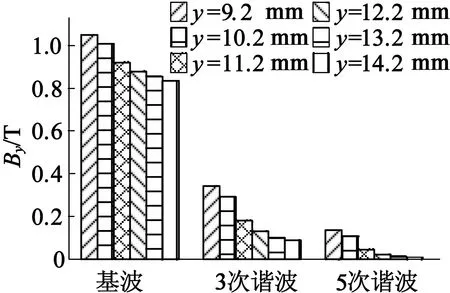
图9 不同位置磁密的谐波分布

当初级绕组在磁场中以1 m/s的速度匀速运动时，绕组交链的磁通开始交变，同时感应出电动势，此时的开路电动势即为空载电动势，其波形如图10所示。在该工况，有限元求得发电机空载电动势峰值为30.9 V，频率为 23.81 Hz。解析结果求得发电机空载电动势峰值为34.3 V，频率为23.81 Hz。

图10 空载电动势波形

有限元结果与解析结果出现较大差距的原因在于，解析法求解时未考虑高次谐波对波形的影响，若单分析基波幅值，如图11所示，那么有限元计算得到的空载电动势与解析结果十分接近，误差在5%以内。

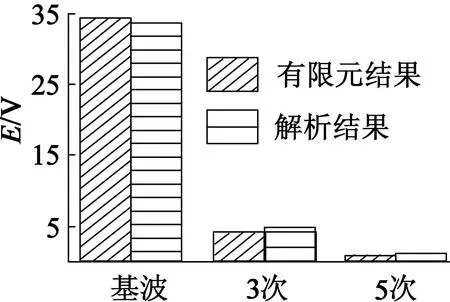
图11 空载电动势各次谐波幅值

利用上文所述的变换方法，将U相电压变换为以2 m/s2加速度加速运动时的波形，并与有限元结果对比，如图12所示。通过g映射关系的变换后，出现变频波形，再通过f映射变换后出现变幅波形，变换所得结果与有限元分析结果十分接近。仅通过有限元分析计算两个周期的电压波形即可通过坐标轴映射变换获得变速运动状态下的多周期波形，较大节约仿真分析的时间。

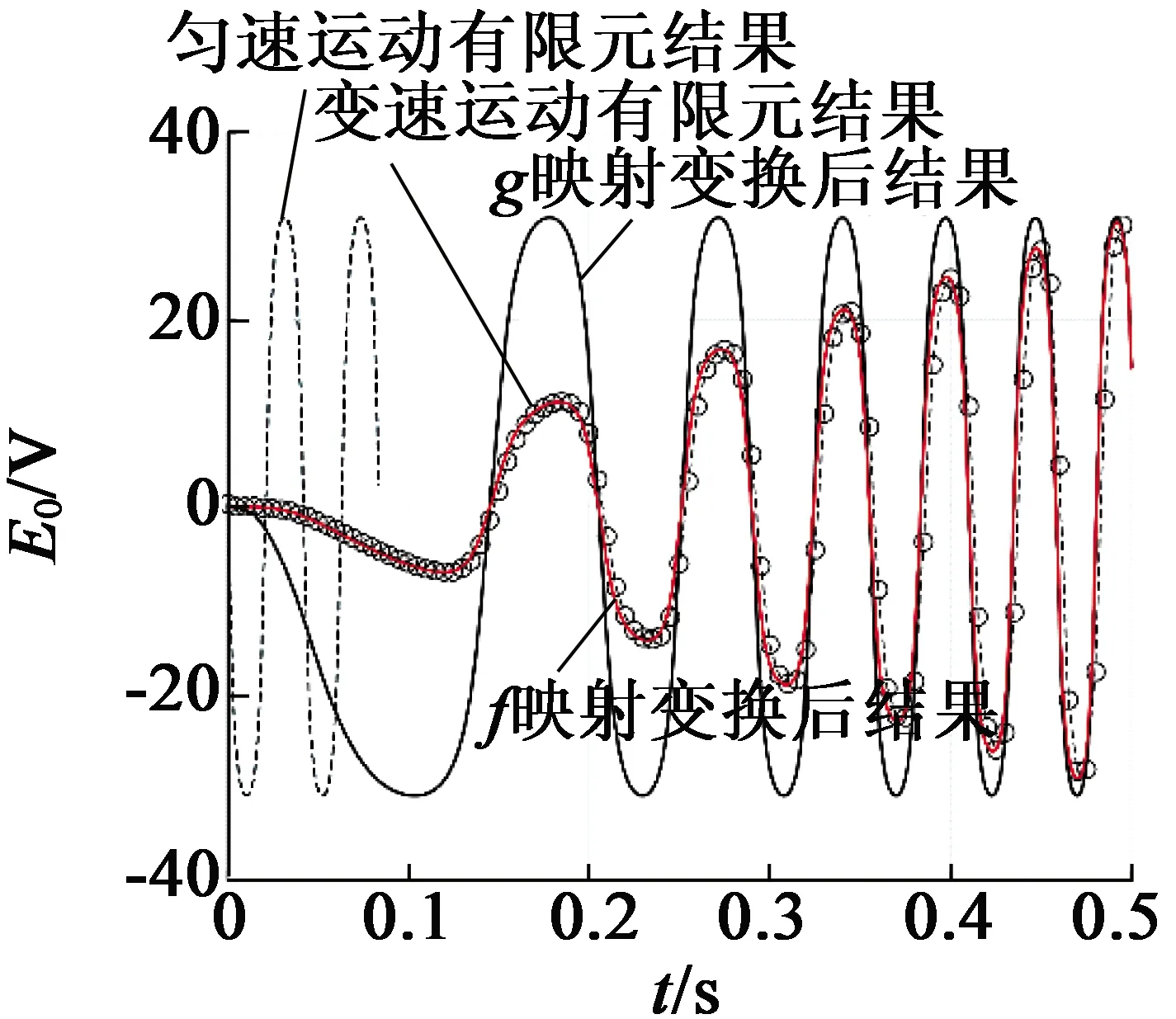
图12 变速运动下空载电动势波形变换

4 样机实验与分析

根据表1给出的参数，加工了一台U形无铁心永磁直线发电机样机，并搭建测试平台如图13所示。

图13 直线发电机拖动实验平台

利用高斯计，测量电机气隙内不同位置的磁密，如表2所示，括号内为计算值。在加工、装配、搬运、实验过程中，发生碰撞导致永磁体轻微退磁会造成气隙磁密有所下降，同时，高斯计的测量准确度也较低。从结果可见，气隙磁密比计算值约小10%。

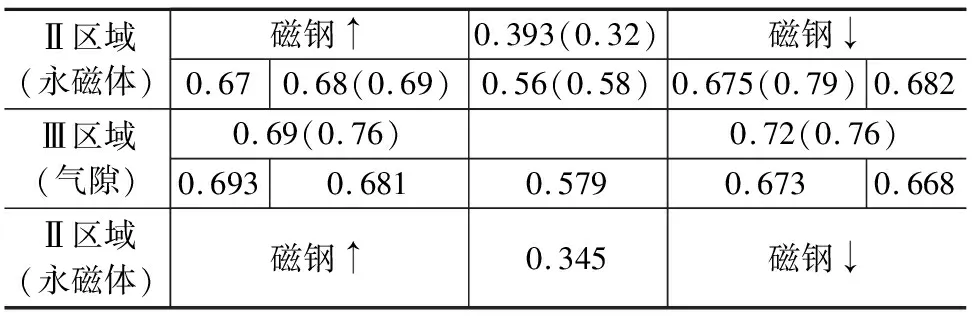
表2 U形无铁心永磁直线发电机气隙磁密 (单位：T)

电机空载拖动时，利用示波器记录U相电压波形，如图14所示。此时，初级运动的速度为0.45 m/s，其中方波形为磁栅尺测量波形，读数磁头扫过磁栅时可以输出方波，方波频率与速度成正比，其关系如下：

图14 0.45 m/s拖动时空载电压波形

v=2×10-4f

(26)

当改变拖动速度时，测量到磁栅尺信号(并换算为速度)、发电机空载电动势峰值如表3所示。

表3 发电机空载电动势

根据表3中数据可以绘得图15。可见，随着次级运动速度的增加，发电机空载电动势上升趋势接近线性，与有限元计算值相差约10%。

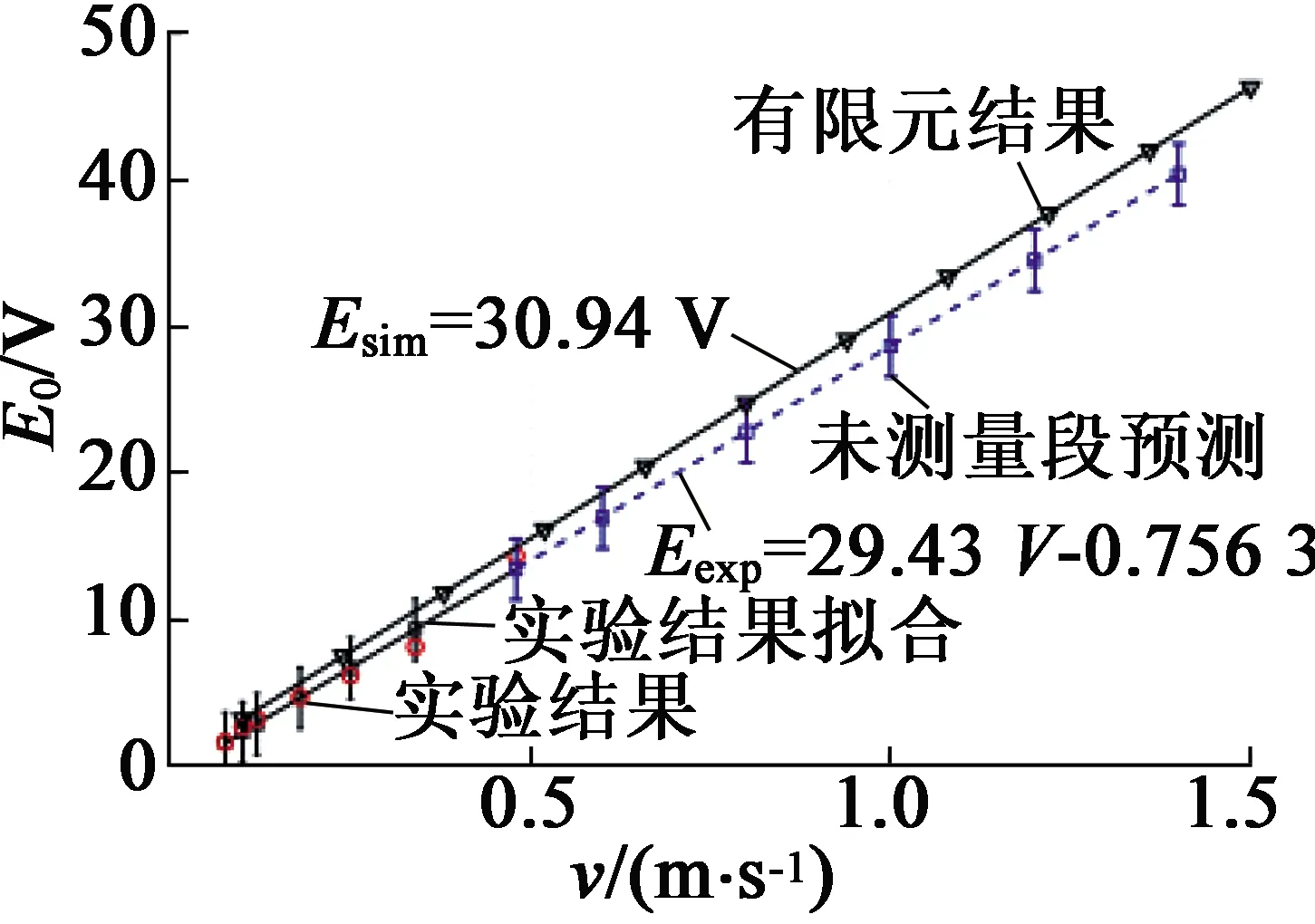
图15 空载电动势实验结果与计算结果对比

5 结 语

本文首先建立了用于波浪能发电的U形直线发电机的物理模型，并提出了两种提高仿真模拟效率的方法。利用对称边界和周期性边界，提出了一种发电机的二维简化模型，根据永磁体排布的周期形，将模型宽度简化为一个极距，并利用对称边界进一步简化为半个镜像模型，引入周期性边界条件和纽曼边界条件来描述因简化模型而带来的新边界。通过简化，减小了求解区域，对解析方法而言，可以减少联立方程组的数量，而对有限元方法而言，可以减少网格数量。因此结合本文的模型，可以节约计算资源。最后通过对比解析方法求得的结果、有限元方法求得的结果和实验结果，得出该模型有效，且精度可靠的结论。同时，为了解决直线发电机往复运动的模式下电机初级一直处于非匀速状态而引起的求解缓慢问题，提出了一种基于坐标变换映射的方法，可以通过仅求解一个稳态周期的波形，并结合坐标系映射，转换到变速运动的状态上去。本文通过有限元模拟验证了这种方法的准确性，而这种方法也在一定程度上节约了计算资源。