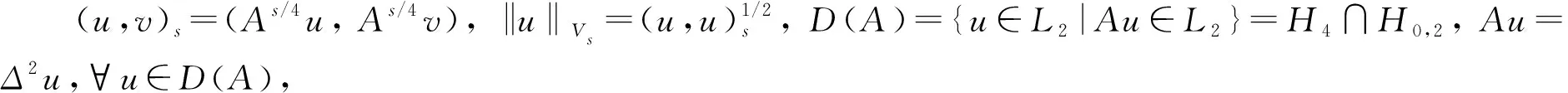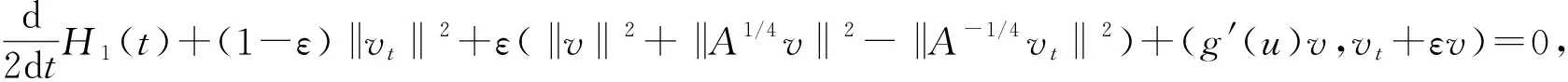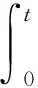RN空间中一类非线性弹性波导方程解的特点

张媛媛

(开封大学信息工程学院, 河南 开封 475000)

Mursaleen等[1]研究了半线性双曲型和抛物型系统的耦合系统边值问题和初边值问题整体广义解和古典解的存在性、唯一性和正则性,这些偏微分方程的非线性系统或耦合系统广泛应用于物理学、化学和生物学等领域．一类非线性弹性波导方程

(1)

可用来描述用黏弹性材料制成的弹性金属杆的振动．在有界区域,具有耗散项的此类方程解的整体存在性和衰减性质已有较多的研究成果[2-7], 但在无界区域此类方程解的特点尚不明朗．Feireisl[8]利用构造1个合适半群的方法讨论了无界区域具阻尼项波动方程解的存在性．受文献[9-11]的启发,本文拟对无界区域下问题(1) Cauchy问题解的整体存在性及其特点进行探讨．

1 预备知识

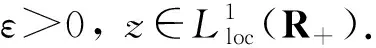
2 主要结论及证明

定理3假定下列条件成立:

i)g∈C1(RN×R), |g(s)|≤C1(|s|p+1), |g′(s)|≤C2(|s|p-1+1), 其中1≤p

ii)f∈H-2, (u0,u1)∈X(RN), ‖(u0,u1)‖X(RN)≤R0, 则问题(1)存在唯一解u, 且(u,ut)∈L∞(R+;X(RN)),u满足‖u‖2+‖ut‖2≤C(R0,‖f‖H-2) (t≥0), 且‖ut‖2+‖utt‖2≤t-2(t2+1)C(R0)e-kt+C(‖f‖H-2) (t>0)．

设Ω=ΩR是无界区域RN中半径为R的球, ‖·‖=‖·‖L2(Ω), ‖·‖p=‖·‖Lp(Ω)．首先,考虑方程在有界区域Ω内对应的初边值问题

(2)

(3)

(4)

‖A1/4ut‖2+‖utt‖2≤C1(t2+1)t-2e-kt+C(R0,‖f‖V-2),t>0．

(5)

(6)

(7)

(8)