弦杆灌浆的方钢管桁架混凝土组合梁受弯承载力试验及数值分析
2020-10-26查志远胡鹏飞仲振鹏
王 琨, 查志远, 胡鹏飞, 仲振鹏
(1. 扬州大学建筑科学与工程学院, 江苏 扬州 225127; 2. 长沙理工大学桥梁结构安全控制湖南省工程实验室, 长沙 410015)
方钢管桁架-混凝土组合梁是以方钢管桁架弦杆、腹杆代替普通钢筋混凝土横纵钢筋所形成的一种新型混凝土组合梁, 为避免钢管受压破坏,还可在上下弦钢管内灌注水泥浆[1-2].与普通钢筋混凝土梁相比, 内置钢桁架的混凝土梁具有承载力高、刚度大、抗震性能好等优点,适用于大跨重载的建筑和桥梁结构[3-4].邓志恒等[5]研究了矩形及T形截面的桁架式钢骨混凝土梁的受弯性能; Zhang等[6]对采用角钢桁架的钢筋混凝土梁进行试验, 结果表明角钢桁架极大提高了钢筋混凝土梁的受剪性能; Arafa等[7]通过有限元模型对不同剪跨比的内置角钢桁架混凝土梁的抗剪性能进行了分析; Colajanni等[8]考察了半预制混合钢桁架混凝土梁的破坏形态和桁架应力的传递机理; Chen等[9]针对波纹钢腹板和钢桁架的组合箱梁提出理论计算模型.以上相关研究结果均表明,以钢桁架替代普通钢筋骨架,可提高混凝土梁的承载力和刚度.
为研究弦杆灌浆的方钢管桁架-混凝土组合梁的正截面受弯承载力, 本文拟通过简支组合梁的竖向静力加载试验,研究试验梁的受力过程、裂缝分布和破坏形态.同时采用Abaqus软件建立有限元模型, 并与试验结果的竖向荷载-跨中挠度曲线和钢管应变变化进行对比, 探讨组合梁的受力过程及工作机理.在试验结果的基础上拟建立弦杆灌浆的方钢管桁架混凝土梁正截面受弯承载力计算方法,为同类组合梁的设计施工提供参考.
1 试验概况
1.1 试件设计
试验主要考察内置桁架的上下弦钢管截面面积和节点间距对试验梁正截面承载力的影响.图1是编号为B-1~B-5的弦杆灌浆的方钢管桁架-混凝土组合梁试件的桁架结构示意图.其中, 试件B-1~B-3比较下弦钢管的截面面积对承载力的影响; B-2和B-5的变化参数为桁架间距; B-3和B-4探讨上弦钢管截面面积对竖向承载力的影响.试件梁长均为2 700 mm, 截面尺寸为200 mm×300 mm, 混凝土强度等级为C40.实测混凝土立方体抗压强度fcu为44.8 MPa, 依据GB/T 50152—2012 《混凝土结构试验方法标准》 计算, 其轴心抗压强度fc为34.05 MPa, 轴心抗拉强度ft为3.2 MPa, 弹性模量Ec为3.36×104MPa.钢管力学性能指标详见表1, 表中fa,fu分别为钢管实测屈服强度和抗拉强度, 钢管的弹性模量Ea按JGJ 138—2016《组合结构设计规范》取值.灌浆料由P·O 42.5普通硅酸盐水泥、UEA膨胀剂(质量比7%)、FDN高效减水剂(质量比0.7%)及自来水以水灰质量比0.4混合而成.实测结硬后灌浆料立方体抗压强度fg为36.3 MPa.
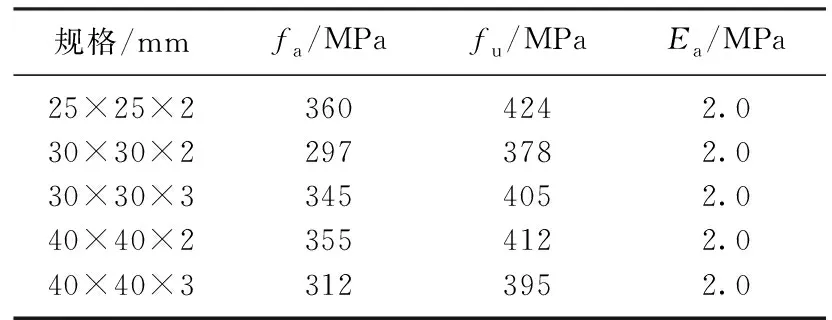
表1 钢管力学性能指标
图2为试验梁加载位置以及应变片布置示意图.试验梁均为简支梁,两端分别采用固定铰支座和滑动铰支座,支座两端各预留100 mm, 试验梁计算跨度均为2 500 mm.试验采用分配梁进行两点集中加载, 竖向荷载P由荷载传感器测量.为了测量各级荷载作用下试验梁跨中挠度Y, 在梁跨中下侧和支座上侧布置百分表测点1~ 5, 应变片(用S表示)布置在钢管桁架上下弦、试验梁跨中混凝土位置.
1.2 试验现象
在竖向荷载作用下,试验梁均发生正截面弯曲破坏,下弦钢管达到完全受拉屈服后,受压区混凝土碎裂.5根试验梁的破坏形态和裂缝分布相似: 在加载初期,试验梁整体处于弹性工作阶段,跨中位移和应变测量值基本呈线性变化; 随着竖向荷载增加,在跨中纯弯段两侧依次出现数条对称分布的竖向弯曲裂缝,且裂缝宽度不断增大、向上延伸; 随着竖向荷载的继续增加, 试验梁上表面混凝土开始出现裂缝, 跨中变形迅速增大,最后试验梁上部混凝土碎裂, 发生破坏.卸载后试验梁具有较好的变形恢复能力和裂缝闭合性能.
试验梁B-1在各级荷载下纯弯区段的平均应变沿截面高度的分布如图3所示.由图3可见,在加载初期, 混凝土和钢管的应变值随截面高度变化基本呈线性变化, 在加载后期, 受压钢管与混凝土之间出现了一定的粘结滑移, 但总体仍符合平截面假定.由于钢桁架上下弦钢管与混凝土之间的粘结能力较弱,笔者建议设计和施工时在钢桁架上下弦表面焊接一定数量的钢筋抗剪连接件,以提高钢桁架和混凝土的粘结性能.
2 数值模型
2.1 材料本构关系
采用Abaqus建立试验梁的有限元模型研究弦管灌浆的方钢管桁架-混凝土组合梁的正截面受弯承载力.方钢管桁架的上下弦杆、腹杆和连杆均采用理想弹塑性模型;混凝土采用Abaqus软件中损伤塑性模型的塑性部分, 其中混凝土单轴受拉和受压应力-应变关系采用双参数模型[10], 并取混凝土剪涨角ψ=30°, 流动势偏移量e=0.1, 混凝土双轴受压与单轴受压极限强度比σb/σc=1.16, 受拉子午线和受压子午线常应力比值Kc=2/3, 为提高有限元程序的收敛性, 本文取黏滞因数μ=0.001[11].
灌浆料的峰值压应变约为0.003~0.004[12], 本文取0.0035.借鉴混凝土单轴受压双参数模型,建立灌浆料的单轴受压应力σ与应变ε的本构关系, 并与试验结果进行对比, 结果如图4所示.结果表明模型与试验结果较吻合, 可用于有限元分析.灌浆料受拉本构关系与普通混凝土相同.
2.2 模型建立
采取分离式方法, 分别建立方钢管桁架和混凝土(含灌浆料)的有限元模型, 如图5所示.方钢管桁架腹杆和联杆未灌浆, 模型建立时采用切割命令将混凝土相应部位挖空, 同时切割出上下钢弦管内灌浆料实体.混凝土和灌浆料均采用四面体单元C3D10, 方钢管、垫块分别采用壳单元S4R和实体单元C3D8R.混凝土内部网格采用自适应网格划分技术,桁架网格全局划分尺寸为15 mm.不考虑方钢管钢桁架、混凝土及灌浆料之间的粘结滑移作用,方钢管桁架与混凝土之间采用embed技术耦合.为了防止应力集中, 试验梁模型的支座和加载点位置设置刚性垫块,并采用tie技术与混凝土绑定.试验梁均为简支梁, 试验梁模型左端设置固定铰支座(x、y、z方向上的位移Ux=Uy=Uz=0), 右端设置滑动铰支座(Uy=Uz=0), 同时采用竖向位移加载方式施加竖向荷载P.
3 结果与讨论
3.1 荷载-跨中挠度曲线
图6给出了试验梁实测与有限元计算的竖向荷载-跨中挠度曲线.对比图6中试验梁B-1、B-2和B-3的P-Y试验曲线可知, 试验梁竖向荷载承载力随着下弦钢管面积的增加而增大; 试验梁B-2和B-5的P-Y实测曲线表明, 桁架节点间距的大小对竖向荷载承载力无明显影响; 试验梁B-3和B-4的P-Y实测曲线表明, 上弦杆钢管截面面积对竖向荷载的承载力也无显著影响.极限荷载的模拟值与试验值较为接近, 两者的P-Y曲线变化规律也相似, 但在加载过程中模型的刚度较试验值大.其原因可能是: 1) 混凝土模型采用的是连续单元, 无法准确计算开裂的影响; 2) 模型未考虑桁架与混凝土之间的粘结滑移.
3.2 荷载-跨中钢管应变曲线
图7给出了试验梁B-1上下弦钢管测点S1和S9处的竖向荷载-跨中钢管应变曲线.如图7所示,模拟值与试验值较接近,下弦钢管在达到极限荷载时均已受拉屈服,而上弦钢管应变随荷载增加基本呈现线性变化,接近屈服.
3.3 受力机理
图8是试验梁B-1的混凝土和方钢管桁架模型在初裂、钢管初始屈服、钢管完全屈服以及破坏等5个特征点下的纵向应变分布.本文以此为例对弦管灌浆的方钢管桁架-混凝土梁的工作机理进行分析.
1) 初裂.由图8(a)可知, 试验梁B-1纯弯段下部混凝土拉应变超过了混凝土极限应变, 表明此部分混凝土开始出现竖向弯曲裂缝.方钢管桁架的应变分布显示, 桁架杆件应力均小于钢管屈服应变, 表明钢管桁架上下弦钢管和腹杆均未达到屈服.
2) 初始屈服.从图8(b)可见, 随着竖向荷载的增加, 方钢管桁架下弦钢管的底面开始出现屈服,此时混凝土在沿试件长度方向的压应变均未超过混凝土的极限压应变, 表明此时混凝土尚未压碎.
3) 完全屈服.由图8(c)可知, 当下弦钢管截面达到完全屈服时,屈服范围约为中间2个节点,此时上侧混凝土没有超过极限压应变,表明混凝土尚未压碎.
4) 破坏.当荷载加载达到破坏时, 桁架下弦钢管屈服范围进一步增大至4个节点, 如图8(d)所示, 此时,试件上侧部分混凝土压应变已超过了极限压应变, 混凝土碎裂, 试件破坏.
综上可知, 当上下弦杆配钢率较为合理时, 弦管灌浆的方钢管桁架-混凝土组合梁破坏形态与钢筋混凝土梁类似, 均呈现为适筋破坏.
4 受弯承载力计算公式
4.1 基本假定
计算弦管灌浆的方钢管桁架-混凝土组合梁正截面受弯承载力时假定: 1) 截面为平面; 2) 灌浆料等同为混凝土材料; 3) 不考虑混凝土的抗拉强度; 4) 混凝土受压应力-应变关系与文献[10]中正截面受弯承载力计算时所用的本构关系相同; 5) 纵向钢管平均应力取钢管平均应变与其弹性模量的乘积,且不超过其屈服强度.
4.2 计算公式
弦管灌浆的方钢管桁架-混凝土组合梁受力时下弦钢管先达到屈服强度, 然后受压区混凝土压碎, 而上弦方钢管一般不会屈服.受压区混凝土的应力图形可简化为矩形, 并取受拉下弦钢管的平均应力为fa, 受压上弦钢管的平均应力为σ′a, 则可建立如图9所示的正截面受弯承载力Mu的应力计算图形.其中,b和h为梁截面宽度和高度;h0为截面有效高度, 取下弦钢管形心至混凝土受压边缘的距离;a′a为上弦钢管形心至受压边缘的距离;α1为等效混凝土抗压强度与混凝土轴心抗压强度的比值,x为受压区高度,Aa,A′a分别为下弦和上弦钢管截面面积.
与截面配筋面积相同的钢筋混凝土梁相比, 弦管灌浆的方钢管桁架-混凝土组合梁正截面受弯承载力较大, 在其正截面受弯承载力计算公式中引入增大因数λ.建立平衡方程faAa-σ′aA′a-α1fcbx=0,Mu=λ[σ′aA′a(h0-a′a)+a1fcbx(h0-0.5x)].其中σ′a=Eaεcu(1-β1a′ax-1)≤fa, 式中εcu为混凝土极限压应变,β1为受压区高度与实际受压区高度的比值.
4.3 计算结果
将试验梁数据带入上述公式, 计算得到试验梁的x、σ′a和λ, 如表2所示.结果显示λ在1.18~1.30范围内, 故取1.24计算试验梁的Mu值, 并与正截面受弯承载力实测值Mut进行比较, 结果见表2.结果表明本文的正截面受弯承载力计算公式与试验结果吻合较好.此外, 为防止截面发生超筋破坏, 受压区高度须满足x≤ξbh0, 其中ξb为相对界限受压区高度.

表2 抗弯承载力计算值与试验值
