呼和浩特市意林与好利来企业品牌竞争模型
2020-10-24赵叶
赵 叶
(北京物资学院 北京 101149)
一、背景
内蒙古意林食品有限公司是一家烘焙食品产销企业,创建于1993年,主营西点、面包,兼营餐饮。现今,意林已开遍了呼和浩特市大街小巷。而呼和浩特市好利来食品有限公司是好利来企业的分公司,于1999年07月27日在呼和浩特市注册成立,主要经营糕点制造,食品零售。前一个是扎根已久的本土企业,后一个是外来入侵的全国连锁企业,像这样的企业之间产生竞争力差别性的因素有很多,其中品牌是产品所有差异项目中最大的差异。品牌之所以成为差异性的关键就在于品牌系统的某一要素突出地满足了消费者的需求,在需求的强度达到一定程度,这一要素所积累的消费习惯转化为营销优势,也就是品牌的核心差异点[1]。
为研究两个企业之间的竞争所产生的现象,本文致力于从经济学的角度来分析具有品牌差别的产品之间的竞争情况,品牌之间的价格竞争我们可以利用Hotelling模型[2]。Hotelling模型是指产品在物质性能上是相同的,但在空间位置上有差异。不同位置上的消费者要支付不同的运输成本,他们关系的是价格与运输成本之和,而不单是价格[3]。
二、模型的基本假设
1.假设呼和浩特市是一个长度为1的“线性城市”,市场中消费偏好沿城市均匀分布于[0,1]之间,分布密度为1。将市场内品牌的竞争归入Hotelling模型,差异性品牌的需求量为D1=(p1,p2,a,b)。a,b分别表示企业1,2品牌产品差异化,且a>0,b>0,1-a-b>0。如图1所示,如果a>b,即企业1的品牌产品相对于企业2的品牌产品具有优势。

图1 线性城市模型
2.假设全市只存在着意林(企业1)和好利来(企业2)两家食品企业,分别位于两端,企业1在x=0,企业2在x=1,出售相同的产品。每个企业提供单位产品的成本为C。
3.消费者购买商品的旅行成本与离商店的距离成比例,单位距离的成本为t假设住在x的消费者如果在企业1购买,要花费tx的旅行成本;如果在企业2购买,要花费t(1-x)的旅行成本。

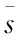
三、模型的建立与求解
考虑两个企业价格竞争的纳什均衡。假定两个企业同时选择自己的销售价格。令pi为企业i的价格,Di(pi,p2)为需求函数,i=1,2。如果住在x的消费者在两个商店之间是无差异的,那么,所有住在x左边的都将在企业1购买,而住在x右边的将在企业2购买,需求分别为
D1=x,D2=1-x。这里,x满足:
pi+tx=p2+t(1-x)
解上式得需求函数分别为:
利润函数分别为:
企业i选择自己的价格pi最大化利润πi,给定pj,两个一阶条件分别是:
二阶条件是满足的。解上述两个一阶条件,得最优解为:
每个企业的均衡利润为:
在以上的分析中,我们假定两个企业分别位于城市的极端。事实上,均衡结果对于企业的位置是很敏感的。考虑另一个极端的情况,假定两个企业位于同一个位置x。此时,它们出售的是同质产品,消费者无品牌的偏好,只关心价格,那么,伯川德均衡是唯一的均衡:
p1=p2=c,
π1=π2=0
更一般地,我们可以讨论企业位于任何位置的情况。假定企业1位于a≥0,企业2位b≥0处假定a+b≤1。如果旅行成本为二次式,即旅行成本为td2,这里d是消费者到企业的距离,那么,需求函数分别为:
需求函数的第一项是企业自己的“地盘”(a是住在企业1左边的消费者,b是住在企业2右边的消费者),第二项是位于两企业之间的消费者中靠近自己的一半,第三项代表需求对价格差异的敏感度。
利润为:
πi=(pi-c)Di
纳什均衡为:
四、结论
上述模型中,这两个主要的企业、区域内竞争、产品同质、完全信息等是Hotelling城市线性模型的主要特点。该模型认为,两个企业具有的品牌差异可以表现为不同地理位置,也可以表现为一维特征空间的不同产品,价格竞争将使价格高于边际成本,从而生产一个长期、稳定的均衡。
