超期服役基坑变形关键影响因素模拟分析

门彬

(中铁城建集团有限公司，湖南 长沙 410000)

在土建工程中，基坑工程规模不断扩大，施工环境日趋复杂。基坑因长期停工对邻近建筑物产生不良影响，易造成地表沉降与变形。目前，国内外关于基坑超期服役的风险研究取得了一些成果。Ding[1]等人基于城市建设的发展，通过三维有限元分析，为基坑的优化设计与施工提供了参考。Zhou[2]等人依托上海地铁10 号线，通过数值模拟，分析了基坑的地表沉降。杨春山[3]等人根据深基坑工程的实际情况，考虑了开挖过程与外部人工变形扰动的影响。通过数值模拟，分析了基坑中的应力与位移规律。Ma[4−5]等人结合实际项目，通过神经网络，进行基坑变形的预测，具有良好的应用前景。陈尚荣[6]等人通过数值模拟，分析了不同支护形式下深基坑开挖对邻近矩形地下通道变形的影响。黄 戡[7]等人通过有限元方法，建立了三维数值模型，分析了基坑降水速度对邻近地铁区间隧道影响的敏感性，并与实际监测结果进行对比分析。应用数值模拟计算，分析与预测基坑结构的变形已日趋成熟。本研究采用有限元法，拟考虑时间效应的影响和锚索预应力损失的时变性，结合《基坑工程手册》[8]与基坑变形分析[9−13]，依托湖南文化广场二期的深基坑工程，对桩锚式支护结构的基坑发生变形的关键因素进行分析，以期为类似工程变形研究提供借鉴。

1 工程概况

1.1 工程概况

拟建的湖南文化广场二期基坑工程开挖深度为17～26 m，施工安全等级为一级，如图1 所示。

图1 项目停工后基坑状况Fig. 1 Foundation pit condition after project shutdown

由于该基坑支护工程中期停工18 个月后，重新复工，已超过其设计使用年限，属于超期服役基坑。通过数值建模分析，得到该超期服役基坑的关键影响因素，为安全施工提供参考与指导。

1.2 控制指标与影响因素的确定

基坑支护结构对基坑和周边环境的安全及顺利施工起重要作用，其结构的应力与变形是基坑工程研究的重要参考指标。在结构材料强度确定的情况下，结构的应力大，小以变形的形式表现。同时，基于结构力学位移法，结构的变形也能反映了结构的受力。所以以支护桩的变形为研究对象，支护桩的水平位移中桩顶位移始终为最大值，且支护桩的竖向位移在基坑的停工阶段无明显变化。因此，选取支护桩的桩顶水平位移作为超期服役基坑研究的控制指标。

考虑超期基坑的实际工程因素和模拟方案设计的可行性，对基坑外侧地面荷载q、支护桩在基坑底部的嵌固深度b、在停工前的开挖深度h及停工时长t作为研究的主要影响因素。

2 数值模拟分析

2.1 计算模型的建立

对湖南文化广场二期基坑东侧基坑开挖剖面建立二维模型，其剖面形状呈长方形，尺寸为50 m×100 m，基坑设计开挖深度为18 m。采用桩径为1.2 m，净距为1 m 的支护桩，作为挡土结构和桩间摆喷止水帷幕。其土层分为3 层：第一层土为粉质黏土层；第二层土为强风化土层；底层土为中风化土层。基坑外土体地面荷载为20 kPa，支护桩高度为23 m。该基坑在开挖11 m 和前3 排锚索施工完成后，停工了18 个月，复工后，继续开挖7 m，并完成后2 排锚索的施工。对该基坑采用具有流变特性的本构模型[11−13]，并基于基坑变形，考虑锚索的预应力损失，利用ABAQUS 软件，进行有限元数值模拟。基于Drucker-Prager 模型的时间硬化幂函数蠕变法，对这3 层土体的黏弹塑性进行模拟，土层物理力学参数见表1。

锚索所采用的钢绞线材料为单向受拉材料，其弹性模量为210 GPa，泊松比取0.3。为便于使用降温法，施加预应力，设定锚索材料的膨胀系数为9.84×10−5，初始温度为20 ℃。在模拟预应力的分析步中，温度值改为0 ℃。在预应力损失的分析步中，温度值改为8 ℃。

表1 土层物理力学性质参数表Table 1 Soil layer physical and mechanical properties

基坑的土方开挖施工，因历时较短，不考虑土体蠕变效应。因为开挖结束后，该基坑停工18 个月，导致放置时间较长，所以须重点监测土体的蠕变效应。由于在停工期间，基坑内、外土体所承受荷载，可视为不变。因此，本次计算釆用TIME 硬化法则进行模拟分析。基坑整体模型、支护桩及锚索结构的模型如图2 所示。

图2 模型有限元网格Fig. 2 Model finite element mesh

表2 基坑模拟计算步Table 2 Calculation step of foundation pit simulation

根据该基坑工程的全部施工过程，建立分析步，每一分析步完成相应的施工任务，见表2。

2.2 模拟方案的设计

将q、b、h和t4 个影响因素的某一个因素作为变量，其余因素不变，进行模拟方案的设计，将基坑在不同工况下的开工、停工、复工及开挖完成的全过程中，支护桩桩顶水平位移随时间变化的数据进行对比分析。

1) 以q作为变量进行模拟分析，分别取10,15,20,25,30 kPa 5 种工况进行计算。

2) 以b作为变量进行模拟分析，分别取5,6,7,8,9 m 5 种工况，进行计算。

3) 以h作为变量进行模拟分析，分别取为5,7.5,10,12.5,15 m 5 种工况，进行计算。

4) 以t作为变量的对比模拟，分别取18,24,30,36,42 个月5 种情况，进行计算。

3 数值模拟结果分析

3.1 地面荷载对支护桩桩顶水平位移的影响分析

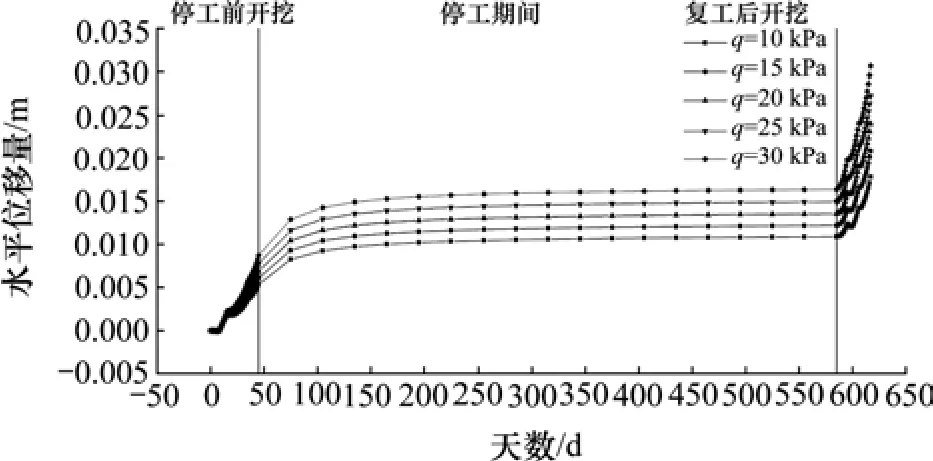
图3 不同外侧地面荷载支护桩桩顶水平位移随时间变化Fig. 3 Influence of different ground load on horizontal displacement of support pile at the top

在不同地面荷载作用下，支护桩桩顶的水平位移随时间变化的过程如图3 所示。从图3 可以看出，基坑外侧地面荷载的增大，基坑在停工前开挖阶段、停工期间和复工开挖阶段，支护桩桩顶的水平位移随着时间的变化，速率不断增大。其中，停工前开挖阶段，桩顶水平位移的增长速率最为明显。而基坑停工和复工后的开挖阶段，桩顶水平位移呈线性增长。基坑施工完成时，桩顶水平位移呈近似线性增长。表明：基坑随着外侧地面荷载的增大，桩顶水平位移的变化速率和最终位移大小，均呈线性增长。

3.2 嵌固深度对支护桩桩顶水平位移的影响

不同支护桩的嵌固深度下，支护桩桩顶的水平位移随时间变化的过程，如图4 所示。

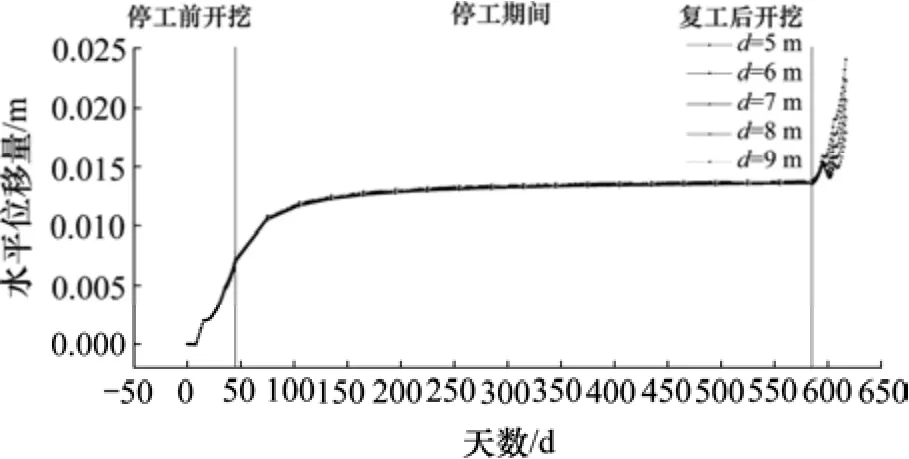
图4 不同嵌固深度支护桩桩顶水平位移随时间变化Fig. 4 Influence of different embedded depth on horizontal displacement of support pile at the top

从图4 可以看出，随着支护桩嵌固深度的增大，基坑在停工前的开挖阶段、停工期间及复工开挖阶段，桩顶水平位移随着时间的变化，速率不断减小。其中，在基坑的停工前开挖阶段和停工期间，桩顶水平位移呈线性增长，但降低幅度极小，可忽略不计。而在停工后开挖阶段的桩顶的水平位移，递减速率较明显。在基坑施工完成时的桩顶水平位移量呈近似线性递减。表明：支护桩嵌固深度对基坑停工前的开挖阶段和停工期间桩顶水平位移的影响较小。而对基坑复工后的开挖阶段影响较明显，在该阶段中，桩顶水平位移随着支护桩嵌固深度的增大，变化速率和位移大小均呈线性递减。

3.3 开挖深度对支护桩桩顶水平位移的影响

基坑停工在不同开挖深度情况下，支护桩桩顶的水平位移随时间变化的过程如图5 所示。

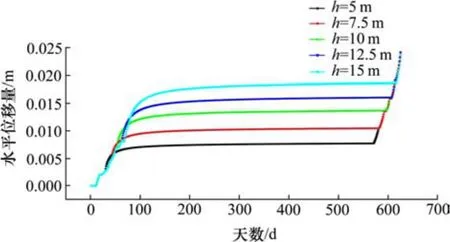
图5 不同开挖深度桩顶水平位移随时间变化Fig. 5 Influence of different excavation depth on horizontal displacement of support pile at the top

从图5 可以看出，停工前，开挖深度的增大，基坑支护桩桩顶水平位移不断增大。而在基坑的停工期间，停工在不同开挖深度情况下，支护桩桩顶水平位移的增长速率，具有相似性，即增长速率前期快，后期逐渐减小。到复工后的开挖阶段，停工在不同开挖深度情况下，桩顶水平位移的增长速率和水平位移均相同。表明：超期服役基坑停工期间和复工后，开挖完成的深度，不影响开挖深度桩顶水平位移的大小。停工时不同的基坑只会影响停工前开挖阶段所导致的桩顶水平位移的大小。

3.4 停工时长对支护桩桩顶水平位移的影响分析

基坑在不同停工时长下，支护桩桩顶的水平位移随时间的变化过程如图6 所示。

从图6 可以看出，基坑随着停工时长的增加，在停工前和复工后的开挖阶段，桩顶水平位移随着时间的变化，速率相似。因为基坑停工时长的增加，基坑在停工期间，前期的桩顶水平位移增长速率不断增长，而后期的增长较小，逐渐趋于稳定。所以对基坑在复工后开挖最终完成时的桩顶水平位移值影响不大。表明：基坑停工期间，由于桩顶位移速率前期大，后期逐渐减小。因此，当基坑停工时长达到桩顶水平位移变化趋于平稳时，若无其他外荷载的变化，其时长的增加对桩顶水平位移值影响不大。

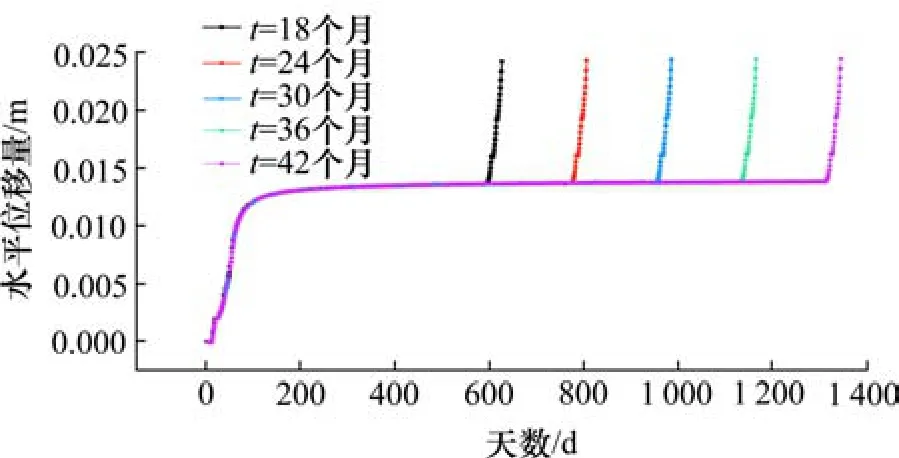
图6 不同停工时长支护桩桩顶水平位移随时间变化Fig. 6 Influence of different stopping time length on horizontal displacement of support pile at the top

3.5 数值模拟与实测数据对比分析

为验证数值模拟计算结果的正确性，对于原数值模拟，考虑其支护桩桩顶在停工期间的水平位移变化和基坑外侧距支护桩10 m 处土体的沉降值，并将其与实测数据进行对比。

在停工期间，支护桩桩顶水平位移随时间变化的数值模拟与实测数据对比，如图7 所示。从图7可以看出，虽然实测数据因测量精度和误差等问题，导致其具有明显的离散性。但是，实测数据与数值模拟计算结果，具有良好的拟合效果。

图7 支护桩桩顶水平位移随时间变化对比Fig. 7 Comparison of horizontal displacement of support pile at the top with time

从图7 可以看出，不论是数值模拟结果，还是实测数据，桩顶水平位移值在停工期间，增长率达到了5%，而桩顶水平位移在该停工期间，前期的增长速率较大，而后期的逐渐减小，趋于平稳缓慢。在停工期间，基坑外侧10 m 处的竖向位移随时间变化的数值模拟和实测数据对比，如图8 所示。从图8 可以看出，实测数据由于测量精度和误差等问题，因此，导致其具有明显的离散性。虽然数值计算结果与实测数据没有良好的吻合。但是二者的变化趋势具有相似性。

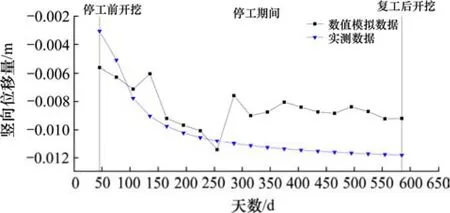
图8 基坑外侧10 m 处的竖向位移随时间变化对比Fig. 8 Comparison of vertical displacement with time at 10 m outside the foundation pit

从图8 可以看出，不论是数值模拟值，还是实测数据，基坑外侧土体的沉降值显著增长。其中，实测数据的增长率达到了63%，而基坑外侧土体的沉降值，在该停工期间，前期的增长速率较大，而后期的逐渐减小，趋于平稳缓慢增长状态。

从数值模拟值与实测数据对比可知，虽然两者在部分数据上存在一定的误差，但总体的变化趋势相近，验证了本数值模拟的正确性。

4 结论

通过数值模拟计算，分析了超期基坑工程时间效应的各种表现形式及产生的原因，时间效应的表现形式是变形随着时间变化而变化。得到的结论为：

1) 超期服役基坑的桩顶水平位移，随着基坑外侧地面荷载的增大，其变化速率和最终位移大小呈线性增大。

2) 在基坑停工前的开挖阶段和停工期间，支护桩嵌固深度对桩顶水平位移的影响较小，而对于基坑复工后的开挖阶段影响比较明显。在该阶段中，支护桩随着嵌固深度的增大，桩顶水平位移变化速率和最终位移大小，均呈线性减小。

3) 超期服役基坑停工前，开挖深度对停工期间及复工后的桩顶水平位移变化规律影响较小，但会影响停工前的开挖阶段所导致的桩顶水平位移的大小。

4) 基坑停工期间，桩顶水平位移的变化规律：前期增长速率大，后期的逐渐减小。则当基坑停工时长达到桩顶水平位移趋于平稳时，其停工期间时长的增大对桩顶的水平位移值影响不大。