基于长短期记忆网络的断面交通数据异常处理
2020-10-24张灵康晋滔成卫
张灵,康晋滔,成卫
(1. 昆明市公安局交通警察支队科信处,云南 昆明 650000;2. 昆明理工大学 交通工程学院,云南 昆明 650504)
各大、中城市交管部门相继引进智能交通系统(Intelligent Transportation Systems,简称为ITS)进行交通管理,积累了庞大的交通原始数据。这些交通数据在传统交通领域和其他领域中,都存有极大的潜在价值[1−2]。因为数据采集、储存质量及精度普遍不高,其平均准确率不足70%[3]。所以交通原始数据的预处理是一项不可或缺的工作。而针对原始数据的异常判定和标准修正是核心工作。最早学者们针对交通数据的异常处理是基于数理统计学原理。通过研究交通数据时间和空间的相关性,结合相应的公式、模型判定异常值。Jacobson[4]等人通过研究交通参数的阈值规律,建立了相关模型,得出了运用阈值来判定参数异常的方法。Zhong[5−7]等人通过改进算法,利用插值和回归方法,修正了异常的数据点。Min[8]等人通过交通数据在时间和空间维度相关性高的特点,使用邻接数据和历史数据等,修正异常值。部分学者对交通数据预处理进行了探索。姜桂艳[9−10]等人针对动态交通数据,建立了一套异常评价标准和数据预处理流程。然而这类统计模型,难以应对呈几何倍数增长的交通数据。
互联网技术快速发展,人工智能算法和深度神经网络开始运用于交通领域。许多学者运用数据挖掘的方法,处理交通数据。杨帆[11]等人利用双向LSTM 网络对船舶自动识别数据进行学习,实现对船舶异常行为进行检测。Sun[12]等基于最邻近算法(K-Nearest Neighbor, 简称为KNN),引入时间窗概念,拓宽数据集规模,利用R 语言,在平台上搭建了基于窗口的最邻近算法。Kim[13]等人对传统递归神经网络进行了优化,采用卷积神经网络(Convolutional Neural Networks, 简称为CNN)和长短期记忆网络(Long Short-Term Memory,简称为LSTM)。结合的C-LSTM (Convdutional LSTM 简称为C-LSTM)模型,对大量历史交通数据进行了训练,建立了不同场景下的模型参数,检测对应的数据异常值。王祥雪[14]等人对交通数据时、空特性进行了识别和强化,完成短时交通流预测模型的搭建。尹 康[15]提出了交通领域的关联时间序列预测模型,在空气质量数据集和交通数据集上,验证了双通道LSTM 法的通用性和有效性。王亚萍[16]等人建立了分层贝叶斯网络下的路网密度估测模型。因此,作者针对断面交通数据的特征,拟运用LSTM模型进行异常数据的筛选及修正工作,提出了一种滑动工作窗口和标签值对比的方法,优化数据筛选和修正流程。
1 基于LSTM 的时序回归模型
1.1 原始数据集标准化处理
由于经典交通流理论存在3 个参数(交通流量、行车速度及车流密度)。因此,对于同一断面的相同时刻,也存在3 个维度的特征向量。因设备采集数据的限制,所以本研究断面的原始数据为流量和速度特征向量。当不同的特征组合时,因为特征本身不同的表达方式和量纲,绝对数值大的数据会覆盖小数据。所以要求对数据进行模型训练之前,先对抽取的特征向量进行归一化处理,以保证每个特征向量在训练模型时,被平等对待。
为了数据集标准化,采用零-均值规范化(z-score 标准化)。经过标准化的数据均值为0,标准差为1。其标准化处理式为:

式中:μ为原始数据的均值;σ为原始数据的标准差;x′为标准化处理之后的数据集;x为原始数据集。
1.2 基于LSTM 的模型简述
原始数据经过标准化处理后,运用LSTM 神经模型开始训练数据。LSTM 实质上是一种特殊的递归神经网络(Recurrent Neural Network, 简称为RNN)。为了解决RNN 网络在处理长时间序列时,产生的梯度消失,LSTM 应运而生。LSTM 网络的核心组成包括5 个部分。
1) 激活函数Tanh和Sigmoid
激活函数Tanh用于帮助调节流经网络的值,确保数值保持在(−1,1),从而控制神经网络的输出值在合理的边界内部。Tanh函数式为:

激活函数Sigmoid与Tanh函数基本一致,不同的是Sigmoid把数据值控制在0 到1 之间。该函数特点:用于更新或忘记数据流携带的信息。Sigmoid函数式为:

2) 遗忘门,可以决定数据信息的去留。其表达式为:
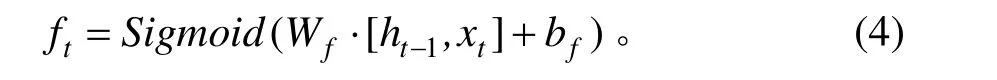
式中:ft、Wf、bf分别为遗忘门的输出向量、权值、偏置;ht−1为前一个隐藏状态的数据信息;xt为当前输入的数据信息。
3) 输入门,可以更新细胞状态。其表达式为:
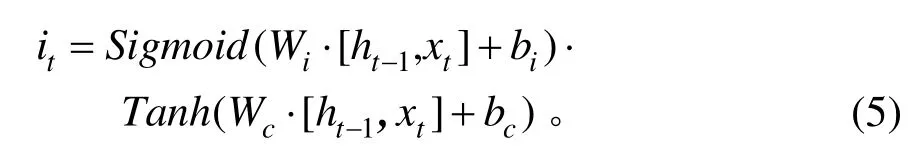
式中:it、Wi、bi分别为输入门的输出向量、权值、偏置;Wc、bc为当前输入状态的权值、偏置。
4) 细胞状态,表示当前细胞储存的数据信息。其表达式为:

式中:Ct、Ct−1分别为当前细胞状态与前一个细胞状态。
5) 输出门,可以计算下一个隐藏状态的值,隐藏状态包含了以前输入的数据信息。其表达式为:
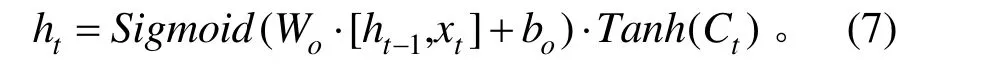
式中:ht、Wo、bo分别为输出门的输出向量(即当前细胞的输出)、权值、偏置。
通过在RNN 简单的细胞结构中,引入门结构产生了LSTM 网络。LSTM 的基本结构如图1 所示。S 代表Sigmoid激活函数;T 代表Tanh激活函数。
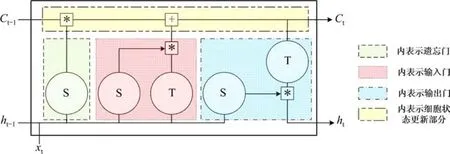
图1 LSTM 基本单元结构Fig. 1 Basic unit structure diagram of the LSTM
2 基于LSTM 的数据异常检测与修正
LSTM 网络对于时间序列的数据,具有优良的回归处理效果,常被用于自然语言序列处理等领域。由于断面交通数据是典型相关性大的时序数据。因此,采用LSTM,进行交通数据的拟合,有充足的前提依据。
2.1 基于Tensorflow 的模型构建
LSTM 网络可通过多种计算机语言编程实现,而基于Python 开发的Tensorflow 框架,为该神经网络的搭建和训练提供了极大的便利。利用Tensorflow,封装的大量神经网络功能和函数,完成几个代码块,即可通过LSTM 模型构建。在Jupyternotebook 平台上,使用其6 个部分,构建了本模型。
1) 导入模型搭建所需函数库及定义常量
先导入Pandas、Numpy 2 种数据处理库和Tensorflow 工具库。同时,为了便于模型可视化,导入Matplotlib 绘图工具库。再定义隐层神经元个数hidden-unit、隐层层数lstm-layers、输入向量维度input-size、输出向量维度output-size 及学习率lr 5 个常量。
2) 导入原始数据
在进行神经网络训练过程中,将原始数据按一定比例分为训练集、验证集及测试集。训练集数据用于模型的训练(对测试集中的异常值,进行检测,并修正),验证集用于模型的性能检测,测试集用于模型的功能使用。
3) 定义神经网络变量
神经网络变量主要包括输入层和输出层的权重、偏置及 Dropout 参数。权重变量采用tf.random-normal 函数,随机向服从指定正态分布的数值中取出指定个数的值。偏置变量采用tf.constant函数,从指定常量值中,取出特定形状的向量。Dropout 参数可以有效减少过拟合现象,使模型泛化性更强。在每个训练批次中,通过随机使部分隐层节点值为0,从而减少隐层节点间的相互作用,减少所训练模型对局部特征的依赖。
4) 搭建神经网络结构
采用tf.nn.rnn-cell.BasicLSTMCell 函数,创建LSTM 基本单元结构。采用tf.nn.rnn-cell. Multi RNNCell 函数,搭建多层LSTM 隐层结构。采用tf.nn.dynamic-rnn 函数,使LSTM 细胞单元结构连接成网络。同时,为了满足神经网络对输入变量的形状要求。需要将输入向量先转成二维进行计算。再将计算结果作为隐藏层的输入。然后将隐藏层输入结果,转成三维,作为LSTM 细胞单元的输入。最后将细胞单元运算结果转成二维,作为神经网络的输出值。
5) 训练模型
在Tensorflow 框架中,基本操作由会话窗口的建立、数据导入字典与传入占位符2 部分组成。在模型的训练过程中,由损失函数和优化器2 部分完成。损失函数使用均方误差法进行计算,优化器选用Adam 自适应学习率梯度下降优化器。在迭代过程中,通过对损失率的观察,判断神经网络的性能。并不断地调节相应参数,使模型损失最小,最终达到收敛。
6) 模型使用及可视化
采用训练完成的LSTM 模型,对测试集数据进行预测拟合,并计算相应的偏差程度。然后使用Matplotlib 绘图工具,对模型计算结果进行可视化。同时,为了便于对模型内部的数据流图有更清晰的认识,利用Tensorflow 中的Tensorboard 工具,对整个模型结构进行可视化。
2.2 基于LSTM 的异常数据检测修正算法
在神经网络的模型训练中,通常的做法:把2/3~4/5 的样本数据用于训练,余下的样本用于测试。但是为了保障模型的准确性,以4:1 的数据划分训练集和测试集。由于模型是对时序数据进行异常检测,参与训练的数据需要无异常点的标准样本。因此,将训练集称为标准样本集,测试集称为异常检测集。算法步骤为:
1) 建立算法工作窗口W
交通检测设备每天采集的流量Q和速度V为二维向量,即X=(Q,V),可以得到一维标签,密度特征K=Q/V。用X表示每天的原始数据集,则X1,X2,…,Xn分别为第一天、第二天、…、第n天的数据。若第t天的数据存在异常点,则获取该天数据为检测集Xt,那么算法工作窗口可表示为:W=
2) LSTM 模型训练及运用
先选取工作窗口W中的标准样本集,导入已经搭建好的LSTM 网络中,通过迭代运算,得到算法所需的模型参数。其次,用模型参数对第t天的数据进行预测拟合,得到备选数据集tX′。由于LSTM 为监督学习深度神经网络,采用密度特征向量K作为标签值,再次训练LSTM 模型,并运用,得到校验标签值tK′。

2.3 基于LSTM 模型的质量控制
为了对断面交通数据进行有效质量控制,采用基于LSTM 模型的检测修正算法,建立完整的质量控制流程。算法流程分为LSTM 模型与数据处理2部分,如图2 所示。
3 样本实验
选取2018 年5 月份昆汕高速公路K2077 断面采集数据进行实例验证。其中,初始标准样本集为5 月1 日−4 日该断面的流量和速度数据集,5 月5日的对应数据集则为异常检测集。同时计算出所需标签值,部分检测集数据见表1。
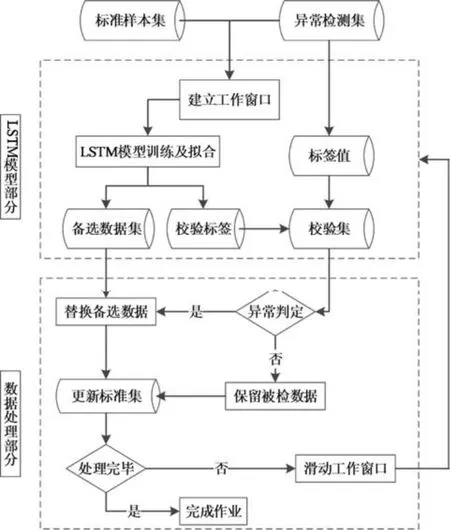
图2 基于LSTM 的交通数据质量控制流程Fig. 2 Quality control of traffic data based on the LSTM
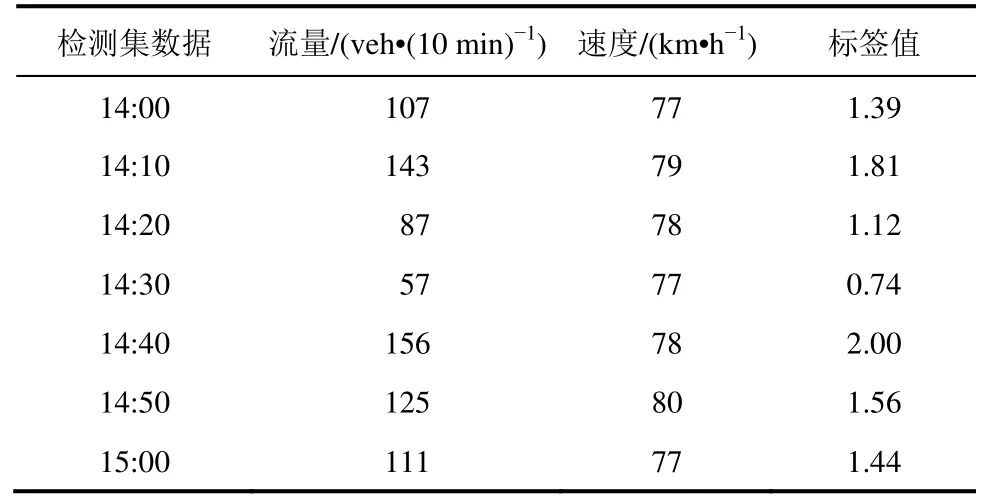
表1 5 月5 日昆汕高速K2077 断面部分检测集数据Table1 Partial test set data of section K2077 of Kunming-Shantou expressway on May 5
3.1 模型运用
将标准样本集导入搭建完成的LSTM模型中训练,并不断优化、调节超参数。最终各超参数取值为:隐层神经元个数hidden_unit=10;隐层层数lstm_layers=2;学习率lr=0.0006;输入向量维度input_size=2;输出向量维度output_size=1;batchsize=60;time_step=20。模型训练迭代过程中,损失函数会随着训练次数的增加而不断降低。直到训练次数达到一定时,即使继续训练,也无法使损失函数明显降低,此时的训练次数可作为合适的迭代次数参数。
在本次实验中,当迭代次数达到50 次时,基本完成收敛。训练模型完成后,调出模型相关参数,运用模型,得出备选数据集和校验标签值。
3.2 异常数据处理
运用LSTM 模型,计算出校验标签值与异常检测集的标签值。采用修正算法进行计算,得到最终的校验集。通过对昆汕高速公路K2077 断面校验集的异常判定,筛选出5 月5 日异常检测集的异常点,对应i分别为:1,13,32,41,59,61,81,83,141。为验证所提出的异常检测算法的实用性,滑动工作窗口,继续对5 月6 日−8 日数据进行检测,从而检测出每个检测数据集中的异常点。为了量化基于LSTM 模型标签值的异常检测算法的检测准确率,计算出5日−8 日检测率分别为 81.82%,83.33%,91.67%,84.62%;误检率分别为11.11%,10%,9.09%, 9.09%。计算结果表明:模型检测率均值超过85%,而误检率均值不足10%。由于实验采用的标准样本集仅为前4 天的数据,训练样本数只有576 个。因此,当数据库的标准样本足够多时,会提高该模型准确率。
针对5 月5 日检测筛选出的异常点,对基于LSTM 模型的备选数据集进行修正替换。更新前后的数据集如图3 所示。从图3 可以看出,异常点位分布较为均匀,基于LSTM 模型的检测算法泛化性能良好,异常检测效果突出。同时,为了对修正结果有更清晰地认识,使用相对误差指标,对5 月5 日检测集的9 个修正值进行量化分析,求出对应时刻索引1, 13, 32, 41, 59, 61, 81, 83, 141 的相对误差,分别为12.68%, 10.26%, 8.51%, 16.21%, 8.69%, 7.16%,15.03%, 7.11%, 10.02%,得到整个修正算法的平均相对误差为10.7%。各个异常点之前的相对误差波动范围均在4.55%以内。表明:基于LSTM 模型的修正算法性能稳定,整体修正效果良好。
3.3 多方法对比分析
基于LSTM 模型修正法,计算得到5 月5 日异常检测集中的异常点位及修正值。将标准样本进行更新后,异常值与修正值对比结果见表2。
在检测集异常点的修正过程中,如果出现某一特征向量修正结果与异常值相同的情况,这是因为LSTM 模型将二维特征向量数据集导入训练时,一维特征的变化程度远大于另一维特征的。所以在数据修正时,会优先考虑修正变化大的特征向量。在本算例分析中,由于所取断面为高速公路数据,速度特征变化极小。因此,会有修正,其结果见表2。
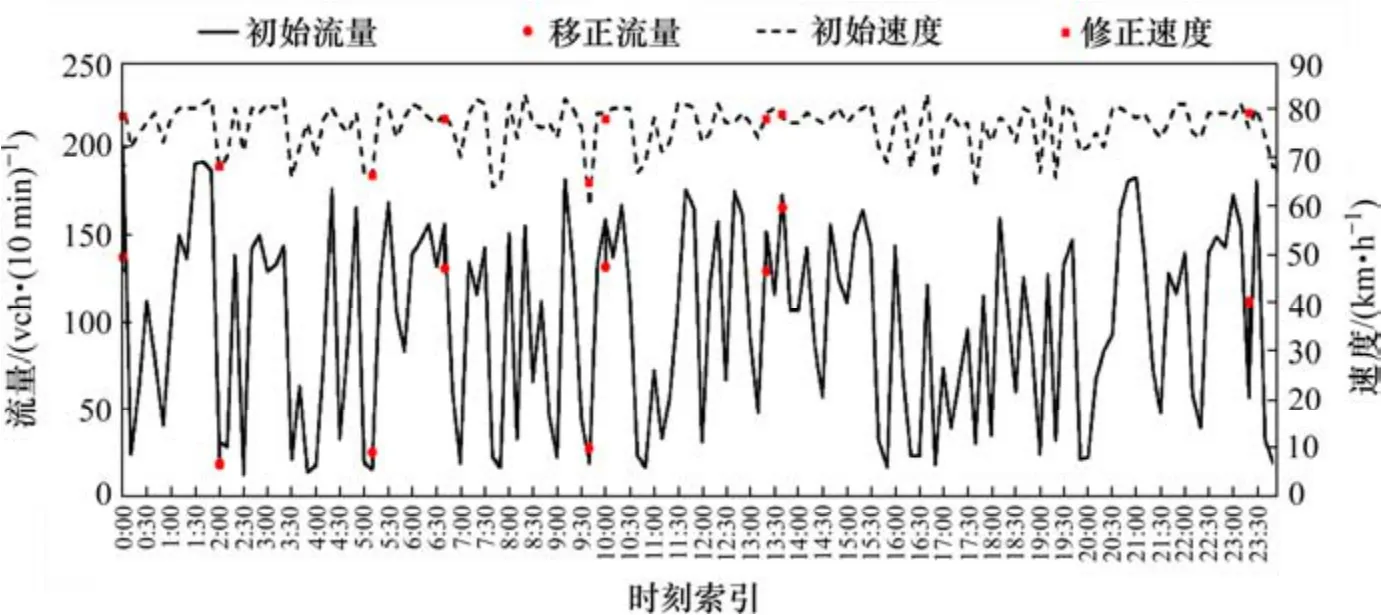
图3 基于LSTM 模型的数据修正Fig. 3 Data correction graph based on LSTM model
为了横向比较基于LSTM模型数据异常处理算法的有效性,选取基于短集合的移动平均修正和基于时间相关的历史数据修正2 种方法作为对比论证。每种方法修正的数据分别与对应窗口数据集的平均值作相对误差(Relative Error,简称为RE)及均方根误差(Root Mean Squared Error,简称为RMSE)计算。3 种方法对异常点的修正误差分析见表3。
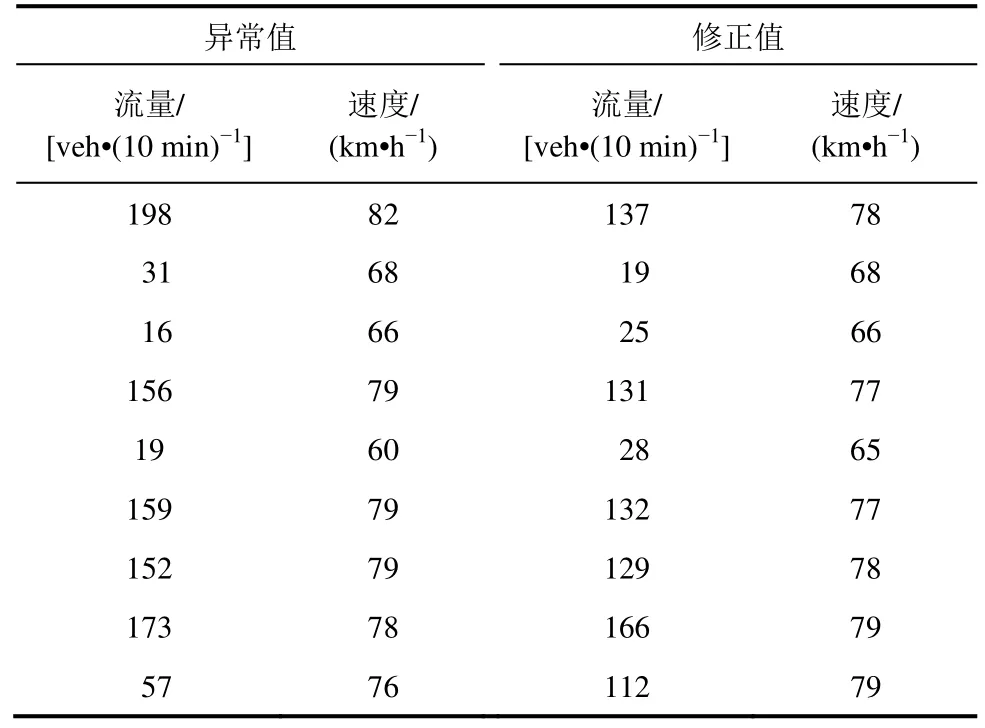
表2 异常数据修正对比Table 2 Comparison of abnormal data correction
从表3 可以看出:①历史数据修正方法实用性较差。虽然交通数据具备时间相关性的特点,但因采集时间间隔较短,数据波动较大。所以基于历史数据的修正方法,会出现较大的误差。②虽然基于邻接数据移动平均的修正方法优于历史数据修正。但是,这种方法对于数据集的内部规律,挖掘不够深入,算法性能不稳定,修正数据时,会出现较大的波动。③基于LSTM 模型,修正算法深入挖掘了数据信息,算法误差小,且具备很强的鲁棒性。在大数据背景下,可以对庞大的交通原始数据进行异常处理。
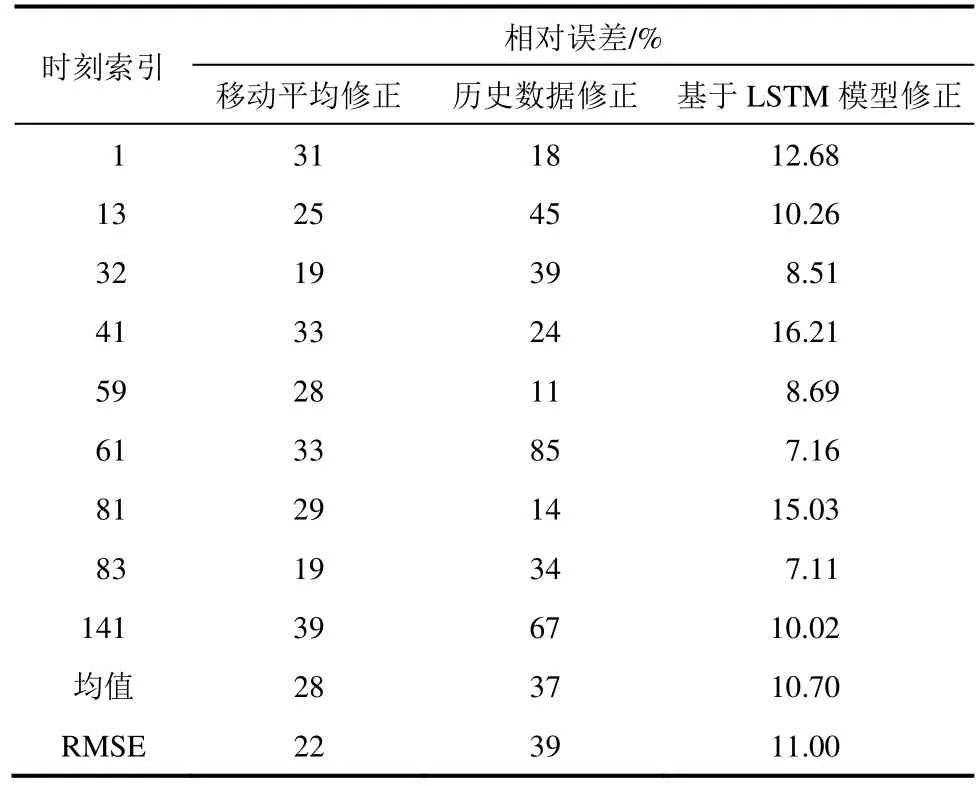
表3 3 种方法误差对比Table 3 Error comparison of three methods
4 结语
原始数据中异常数据的检测与修正是预处理过程中的核心环节。本研究提出了基于LSTM 模型的数据异常处理算法,得到的结论为:
1) LSTM 模型对交通时序数据训练结果,表现优异,可快速处理大量原始数据。
2) 检测修正算法从整体上优化了数据质量,弥补了传统算法的局限性。
3) 工作窗口的建立,精简了算法流程,提升了数据修正的精度。由于深度学习的要求,需要质量高的大量历史数据作为样本训练,因此,有待进一步研究。
