精确制导弹药延寿阶段贮存可靠性预测模型研究∗
2020-06-11赵建忠席建峰李冠峰
薛 敏 赵建忠 席建峰 李冠峰
(1.海军装备部装备项目管理中心 北京 100089)(2.海军航空大学 烟台 264001)
(3.中国人民解放军91181部队 青岛 266000)(4.中国船舶重工集团公司第七一三研究所 郑州 450007)
1 引言
在现代信息化作战及高技术战争中,精确制导弹药的作用越来越重要,地位越来越显著。由于精确制导弹药是“长期贮存、一次使用”的装备[1],其研制过程需要耗费大量的人力、物力和财力,并花费相当长的时间,因此,当精确制导弹药贮存到其规定贮存期限,经检测可以继续使用,暂不进行退役处理而继续服役,称为超期服役精确制导弹药。
超期服役精确制导弹药,由于长时间的贮存、检测和故障维修等引起导弹内部材料性能发生变化,从而导致其贮存可靠性下降,使用风险增大[2~3],因此分析超期服役精确制导弹药的可靠性变化规律,研究延寿阶段可靠性预测模型,对于减少使用风险、最大限度地满足作战需求,具有十分重要的军事意义。
2 超期服役精确制导弹药的可靠性变化规律
2.1 超期服役精确制导弹药的寿命剖面分析
寿命剖面是指对产品从出厂交付到完成其任务使命(包括返厂大修、最终耗损、报废或者退役)这个时间段上的各种事件和环境的描述[4]。
超期服役精确制导弹药寿命剖面和正常服役精确制导弹药的寿命剖面一样,都是一种长期贮存并一次使用的产品,除了按规定进行定期检测和维护外,主要处于贮存状态,当精确制导弹药处于战备阶段时,也通常处于战勤值班、待命停放状态,当处于执行任务期间,完成精确制导弹药的投射,其飞行任务时间是很短的,而其贮存时间可以长达10年,甚至更长的时间。
从超期服役精确制导弹药的寿命剖面图可以看出,超期服役阶段与正常服役阶段基本相同,所不同的是虽然都经过贮存、检测、维护以及运输等事件,但是其事件的内容(比如频率、数量等)也有很大不同。

图1 寿命剖面简图
2.2 超期服役精确制导弹药可靠性变化规律
和正常服役精确制导弹药一样,超期服役精确制导弹药贮存期间除了要经历库房内贮存外,还要担负战备值班、演习训练、科研试验等军事任务。在此期间,超期服役精确制导弹药储存期间的可靠性不仅受气候环境因素、生物环境因素、运输环境因素等影响,还会受人为因素的影响[5]。为了保持超期服役精确制导弹药高可靠性,一般采取定期检测和维修等手段,使其可靠度维持在较高水平,至少不低于其规定的最低可靠度要求。因此,定期检测和维修对超期服役精确制导弹药的可靠性影响较大。
对于储存产品经过定期检测和维修后,其产品的可靠度一般有三种情况,第一种情况是修复后的产品的可靠度可以恢复到最初的水平;第二种情况是修复后可靠度有所提高,但是不能恢复到上个检测点的水平;第三种情况是经过定期检测和维修后,不仅产品的可靠度不能恢复到上个检测点的水平,呈现下降趋势,而且在贮存期间产品的故障率有增大的趋势[6~7]。
由于超期服役精确制导弹药在定期检测维修中,只是对局部的某些部件进行更换或修复,并非全局的更换修复,并且在检测维修中需要进行通电、断电等操作,加之环境应力等的影响,都会对精确制导弹药的可靠性产生一定的影响,因此,考虑到更换件与不更换件的共同作用、检测维修以及环境应力的影响,超期服役精确制导弹药的贮存可靠度会出现下降的趋势,且在每个定期检测周期内故障率函数发生变化,故障率不断增大,即超期服役精确制导弹药的贮存可靠度变化规律属于第三种情况。如图2所示。
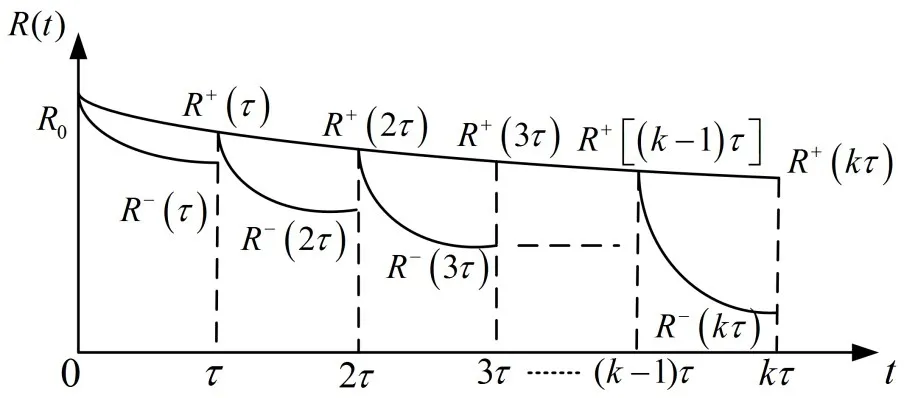
图2 第三种情况
3 超期服役精确制导弹药可靠性预测模型
3.1 模型假设
根据超期服役精确制导弹药实际情况,做以下模型假设:
1)超期服役精确制导弹药初始可靠度为R0≤1;
2)不修复条件下,贮存寿命t服从参数为θ0的指数分布,在第k次检测修复后的贮存寿命服从参数为θk的指数分布,且θ0≥θ1≥θ2≥…≥θk-1≥θk;
3)定期检测时间间隔为τ。
3.2 初期服役精确制导弹药贮存可靠性预测模型[8~12]
根据超期服役精确制导弹药的可靠性变化规律及模型假设,超期服役精确制导弹药的初始可靠度为R0,不修复条件下,贮存寿命t服从参数为θ0的指数分布,在第k次检测维修后贮存寿命服从参数为θk的指数分布,且有:
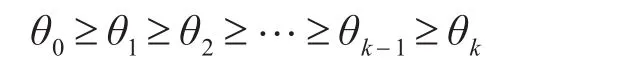
对于超期服役精确制导弹药的贮存可靠性,分为两个部分来考虑,一是超期服役初始可靠度R0;二是在假定超期服役贮存之前完好无损的情况下,精确制导弹药贮存可靠性随贮存时间t影响而发生变化的条件贮存可靠度Rs(t;θ)。因此超期服役精确制导弹药的贮存可靠性可以用数学模型描述:
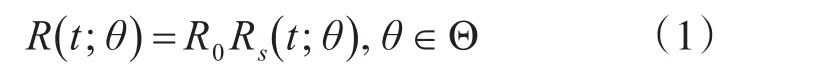
由于精确制导弹药在超期服役期间,定期检测间隔末端的贮存可靠性下降主要是由于精确制导弹药的更换件与不更换件共同作用引起的,因此在分析超期服役精确制导弹药贮存可靠性时,将其分为两个子系统来看待,其中子系统1为不更换件,子系统2为更换件。
子系统1由电子元件、机械部件、机电部件等组成,其可靠度服从指数分布,设超期服役精确制导弹药子系统1的条件贮存可靠度为Rs1,则其分布公式如式(2)所示。

式中,Rs1为超期服役精确制导弹药不更换件条件贮存可靠度;δ为寿命退化系数。
子系统2为更换件,该子系统由于需要定期检测和维修,检测间隔之间的故障率随贮存年限的变化而增大,根据3.1模型假设2,θ0≥θ1≥θ2≥…≥θk-1≥θk,由于超期服役精确制导弹药的故障率λ=1θ,因此超期服役精确制导弹药 第k次检测修复后的故障率λk=1θk,有λ0≤λ1≤λ2≤…≤λk-1≤λk,根据工程实际经验以及超期服役精确制导弹药贮存可靠性变化趋势示意图,假定超期服役精确制导弹药在第k次检测维修后的故障率满足式(3)。
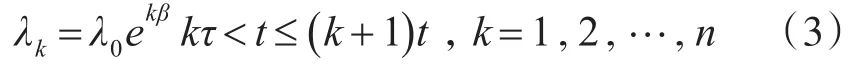
即
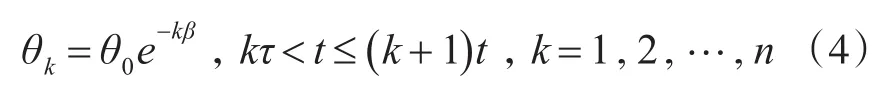
式中,β为退化因子,λ0为超期服役精确制导弹药初始故障率,θ0为超期服役精确制导弹药初始贮存寿命。
设超期服役精确制导弹药子系统2的条件贮存可靠度为Rs2,则其数学模型为
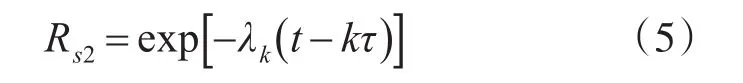
根据式(1)~(5),可得
因此根据式(1)~(6)可得,超期服役精确制导弹药的贮存可靠性为
在第k次检测前时刻,超期服役精确制导弹药的贮存可靠度为
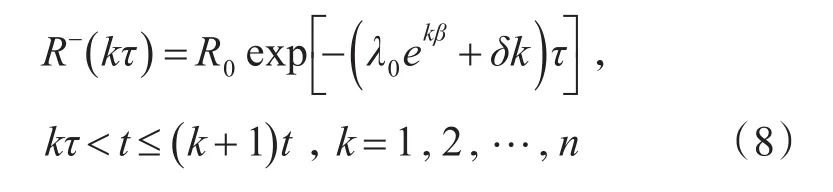
在第k次检测后时刻,超期服役精确制导弹药的贮存可靠度为
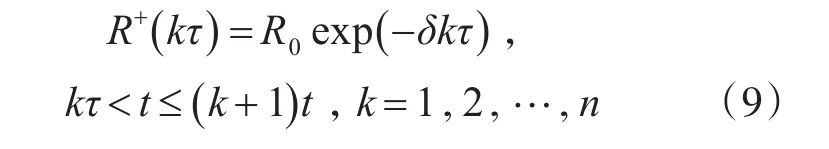
该模型中,初始贮存可靠度R0的估计采用极大似然估计法,对参数λ,δ,β采取最小二乘估计。
4 超期服役精确制导弹药可靠性预测模型应用
以某型导弹为例,该型导弹已达服役年限,正处于超期服役阶段,经过能力分析评价,该型导弹仍可以满足现阶段军事需求,完成作战任务。假设超期服役导弹初始可靠度R0=0.99,通过定期检测与试验性检测,可以得到该型号导弹的系统故障率统计数据如表1所示。

表1 某型导弹系统故障率统计数据
依据表1给出的数据,并运用可靠性预测模型,可以求得退化因子β=0.1396,λ0=0.083,寿命退化系数δ=0.0205,因此可以求得超期服役导弹的贮存可靠度为
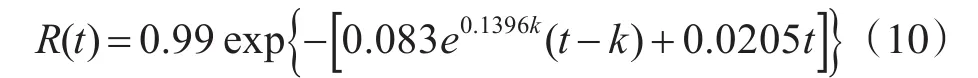
由此也可以根据可靠度的定义,得到超期服役导弹贮存寿命分布。

5 结语
本文在分析超期服役的精确制导弹药贮存可靠性规律的基础上建立了出期服役精确制导弹药可靠性预测模型,模型揭示了定期检测维护与贮存可靠性的关系,运用此模型可以根据前k-1次的检测数据预计第k次检测前和检测后超期服役精确制导弹药的贮存可靠度,同时得到超期服役精确制导弹药的贮存寿命分布。本文从导弹贮存的角度提出了一种简单实用的超期服役精确制导弹药可靠性预计模型,对于预测精确制导弹药的可靠性和精确制导弹药的寿命具有一定的实用性。
