深海采矿循环式水力集矿系统设计与数值研究

赵伟杰，肖龙飞，赵国成，刘明月

(上海交通大学 海洋工程国家重点实验室，上海 200240)

在蕴藏丰富的深海矿产资源中，锰结核因其储量大、分布广、丰度高而具有重要开采价值。锰结核的采集主要存在两类方案：一类是以电机驱动阿基米德螺旋结构或旋转链齿等机构，从而掘取矿物的机械式系统；另一类是以泵为动力，通过流体力采集矿物的水力式系统[1]。其中机械式系统采集效率较低，难以满足经济性要求[2]，水力式系统则具有效率高、可靠性好等优势[3]。目前中国的鲲龙500海底集矿车、比利时的Patania II[4]、韩国的MineRo II[5]等均采用水力集矿系统。

目前关于水力集矿的研究主要集中于集矿头部分，并主要以锰结核等粗颗粒为研究对象。Yang和Tang[6]提出一种水射流式集矿装置，通过试验研究了主要的几何及工况参数对采集效果的影响。Lee等[7]提出一种基于射流附壁效应(Coanda effect)的集矿装置，通过试验测量了其采集率。赵国成等[8]通过试验研究了锰结核在抽吸式集矿头流场下的受力规律，总结了颗粒受力及其尺寸、位置等变量之间的关系。无论采用水射流式还是抽吸式集矿头，均不可避免地将海底沉积物细颗粒带入集矿机中。由于集矿机连续工作的特性，将混有海底沉积物细颗粒的尾水直接排出集矿机是目前普遍的做法。

然而，随着环保问题日益受到关注，环境影响已成为水力集矿系统设计的重要考量。美国深海采矿环境研究项目(DOMES)报告指出，集矿造成的海底沉积物的扩散与再沉积可能对底栖生物群落及鱼类幼体产生影响，此后德国DISCOL、日本JET等项目研究结果均支持上述观点[9]。近年来有更多研究[10-12]基于实验室和海底原位试验结果，提出集矿作业排放的海底沉积物可能造成海底生态及生物多样性的破坏。因此水力集矿系统应当考虑对海底沉积物进行处理，在实现高效集矿的同时，减少尾水对环境的影响。

提出一种新型的循环式水力集矿系统，通过“矿—沙分离”及“水—沙分离”步骤，实现集矿系统内部细颗粒的分离、浓缩、储存、排放。采用基于欧拉法的液固两相流模型，对该系统的核心构件(即两组分离器)进行数值模拟，并对其分离效果与流场特征进行评估与分析。

1 设计方案

循环式水力集矿系统的设计思路如图1所示。相较于现有的水力集矿系统，方案增加了矿—沙分离器和水—沙分离器，使进入系统的水及海底泥沙颗粒(图中简称“沙”)在系统中循环，从而控制泥沙颗粒的排放。根据以上思路，提出如图2所示的设计方案。其工作原理是：集矿头A贴近海床表面，泵工作时其内部形成抽吸流场，使得海床表面的锰结核与泥沙被吸入管道。当锰结核随水流到达矿—沙分离器B上部的水平管道时，因锰结核浮力与升力之和远小于自身重力且管道足够长，所以锰结核落入竖井并在多孔挡板的引导下落入给料机F，随后通过输送装置G连续输送至扬矿系统，并可通过矿浆泵实现逐级提升[13]。矿—沙分离器B内的泥沙则由于难以沉降而随水流通过泵C进入水—沙分离器D。水—沙分离器借鉴了气—固两相流惯性分离器的设计[14]，其内部的槽形挡板可促进泥沙颗粒沉降。当底部的泥沙积累到一定量时，将分离器箱体的底板打开，使泥沙缓慢排放到海床表面。水—沙分离器相当于对泥沙颗粒进行过滤。过滤后的水有少部分通过调节阀E以较低流速流入矿—沙分离器B，将竖井内的泥沙自下而上带入水平管道，防止其在竖井内沉积；其余大部分水流入集矿头A，形成一定强度的射流，以使矿物与沉积物的原生状态瓦解并将混合物吸入集矿系统中，最终形成循环。

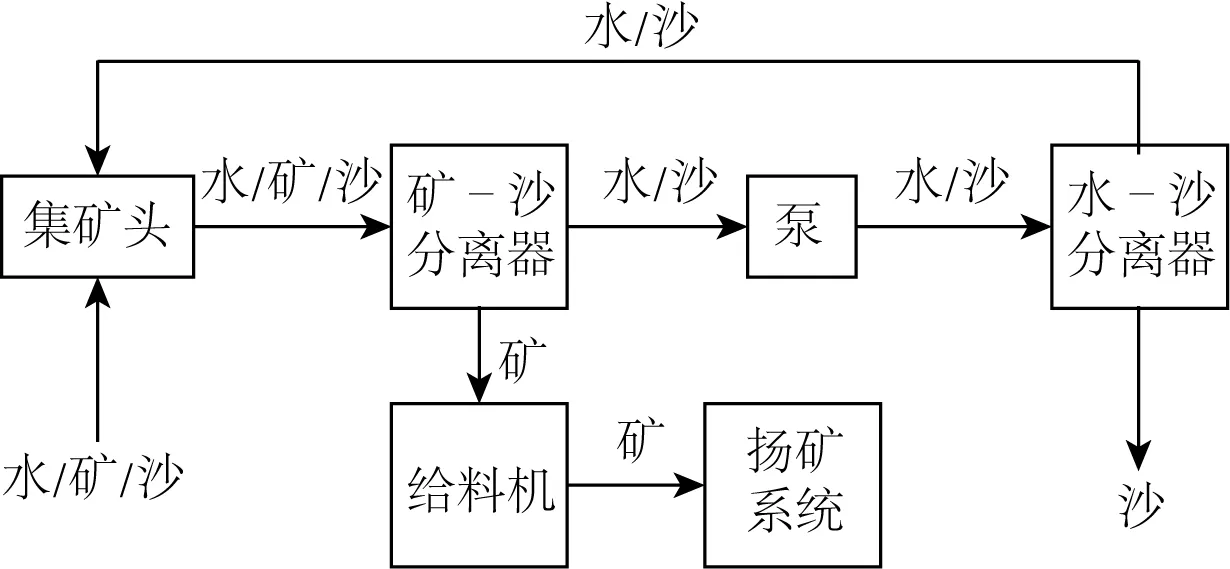
图1 设计思路示意Fig. 1 Sketch of design concept

图2 循环式水力集矿系统示意Fig. 2 Sketch of circulating hydraulic collecting system

2 数值计算模型

2.1 控制方程

采用欧拉液固两相流模型，模拟水和泥沙颗粒组成的混合物，其中水为连续相，颗粒为离散相。由于颗粒浓度较高，故而采用欧拉模型计算相较于拉格朗日模型更经济。该模型连续性方程为[15]：

(1)

(2)

其中，下标f,s分别代表液相和固相；αf,αs为二者体积浓度；ρf,ρs为二者密度；vf,vs为二者速度矢量。

动量方程为[15]：

(3)

(4)

其中，p为静压力；ps为颗粒相互作用形成的固相压力；τf,τs为二者切应力张量；g为重力加速度；Ksf,Kfs为相间动量交换系数；Cvm为虚拟质量力系数，取0.5；CL为升力系数，取0.25。

相间拖曳力采用Richardson-Zaki模型[16]，其特别适用于非变形的细小圆球颗粒，能够模拟颗粒浓度变化所产生的效应。式(3)和(4)中的Ksf,Kfs可表示为：

(5)

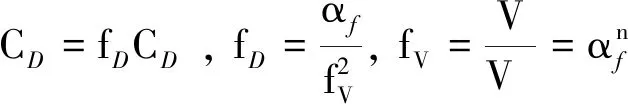
(6)

其中，CD，CD∞分别为颗粒群与单颗粒的拖曳力系数；V，V∞分别为颗粒群与单颗粒的静水沉降速度；n为Richardson-Zaki指数；afs为液固两相间相互作用面积密度。以颗粒体积浓度αs与颗粒直径ds表达afs：

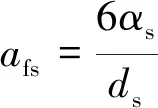
(7)

根据多次计算与试验资料比对，取CD∞=0.1,n=5.5。

2.2 湍流模型

液相湍流模型采用标准k-ε模型。此时液相雷诺应力张量τt,f为[15]：

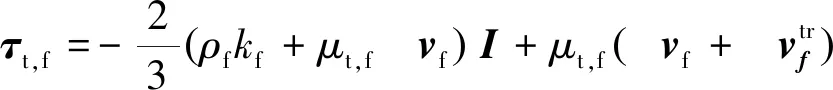
(8)

(9)

其中，Cμ为系数，取0.09；kf为液相湍流动能，εf为液相湍流耗散率。

固相湍流采用Tchen湍流响应模型。该模型通过建立离散相(固相)与连续相(液相)的湍流脉动速度之间的关系，进而以液相湍流物理量表达固相湍流。此时液相与固相的湍流扩散系数分别为[17]：

(10)

其中，qij表示第i相与第j相的湍流脉动速度的内积在第j相上的平均值，即：

(11)

τT,τI,τR均为与湍流有关的特征时间尺度，其表达式为[17]：

(12)

其中，σ0为湍流普朗特数，取1.0；Cβ为系数，取1.8。系数ξ的表达式为：

(13)

其中，vr为固相相对于液相的滑移速度。

2.3 模型验证

为验证以上计算模型的准确性，以Roco和Shook[18]及Gillies等[19]的试验资料为对照，计算两组实例，其描述的物理问题均为水—沙混合物在水平圆管中的流动，具体的条件如表1所示。

表1 计算实例的几何与物理条件Tab. 1 Geometrical and physical conditions of simulation cases

计算区域长度均取50D，以使流动充分发展并达到稳定状态。考虑到颗粒浓度分布是主要关心的量，并且是流体与颗粒之间各种相互作用的最终结果，因此选取管道末端横截面，在重力方向上划分若干微元，对于每一个位置(高度)y计算出颗粒体积浓度平均值，并与试验值比较，如图3所示。图中曲线为计算值，散点为试验值，可以看出两者较为吻合，验证了液固两相流计算模型在一定条件下的准确性。

图3 数值计算结果与试验资料比较Fig. 3 Comparison of numerical results and experimental data

3 数值结果与分析

3.1 矿—沙分离器

矿—沙分离器模型如图4所示，其对应图2中T字形结构下部的竖井及与之相连的封闭区域；假定其上部水平管道距计算区域足够远，故模型中未考虑该部分。竖井长0.7 m，横截面为边长0.2 m的正方形；竖井右侧有通道与封闭区域相连，二者之间截面称为纵截面；竖井中部均匀排列11根圆柱，间距为20 mm(小于多数锰结核直径)并可视作与横截面成30°夹角的有缝隙的挡板。矿粒从上落下(计算时未考虑矿粒)，水—沙混合物(颗粒直径取0.165 mm，体积浓度取10%)以较低流速自下而上流动。根据陈光国等[20]给出的锰结核在管道中静水沉降速度公式，若假设锰结核为直径5 cm的球形，取管道直径为0.2 m，则锰结核静水沉降速度约为1.02 m/s。故计算时水—沙混合物入口流速不超过1 m/s，以保证锰结核顺利沉降。

矿—沙分离效果以泥沙颗粒溢出流量与溢出率来衡量。其中溢出流量表示泥沙颗粒单位时间通过图4所示纵截面进入给料机的质量；溢出率表示溢出流量与入口总颗粒流量的比值。以上两变量随入口流速的变化呈相似规律，如图5所示。入口流速0.4 m/s时泥沙颗粒溢出流量达1.42 kg/s，入口流速0.6 m/s时为0.50 kg/s，可见在入口流速0.4～0.6 m/s范围内，随着入口流速增加，泥沙颗粒的溢出可以得到有效的抑制。入口流速0.6 ～1.0 m/s范围内，溢出流量仍持续降低，而降幅则逐渐减小。

图4 矿—沙分离器模型Fig. 4 Nodule-sediment separator model

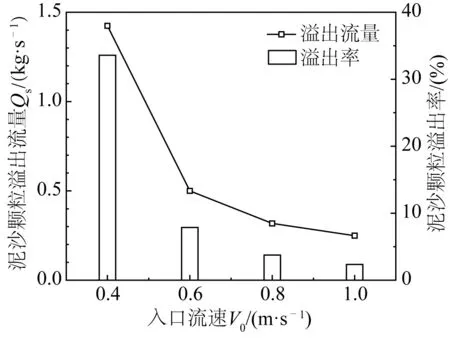
图5 泥沙颗粒溢出流量与溢出率Fig. 5 Sediment particle spillage flowrate and percentage

分析竖井内的泥沙颗粒体积浓度分布，如图6 (a)～(d)所示。入口流速0.4 m/s时，靠近通道侧的水—沙混合物通过挡板后，速度方向发生变化，产生明显的水平分量，而竖直分量不足以提供颗粒向上运动的拖曳力，故而大量颗粒涌入通道，随即沉降至底部并沿壁面流入给料机。入口流速0.6 m/s时，颗粒通过挡板后仍能顺利上升，仅在竖井上部与通道连接处有溢出现象，其原因是该处水质点本有向上运动的倾向，遭遇连接处壁面后产生流动分离，一部分继续向上运动进入竖井，另一部分携带颗粒进入通道并沉降。入口流速大于0.6 m/s时，竖井上部与通道连接处的颗粒溢出现象更弱，流入给料机的颗粒量进一步降低。

计算结果表明竖井的设计能有效降低流入给料机的颗粒量。若取消竖井的设计，使流有泥水混合物的水平管道与下方的给料机直接相连，则分离效果不理想。如图6(e)所示，将原计算模型顺时针旋转90°并取消圆柱挡板，重力方向仍竖直向下，混合物从左向右流动，颗粒直径同为0.165 mm，入口速度1.0 m/s，体积浓度10%。计算稳定时，流入下部给料机的颗粒流量达1.46 kg/s。

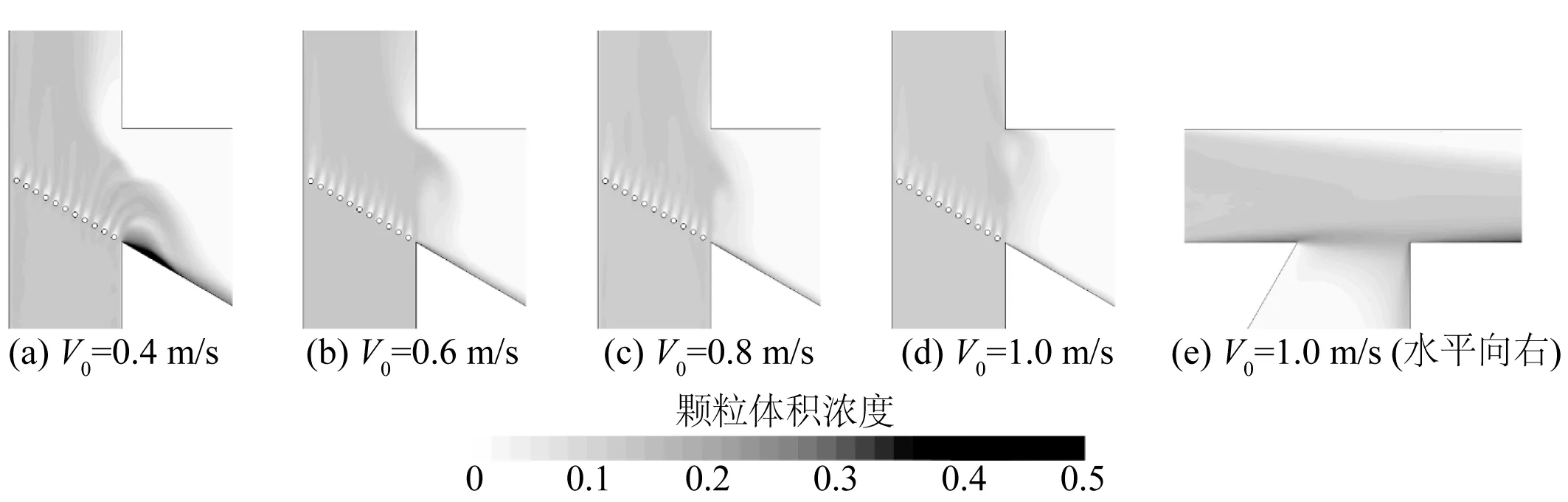
图6 泥沙颗粒体积浓度分布Fig. 6 Distribution of sediment particle volume concentration

3.2 水—沙分离器

水—沙分离器模型如图7所示，其对应图2右下部分。箱体长1 m，宽和高均为0.4 m；箱体两端上部与直径0.2 m的管道相连，左侧为水—沙混合物入口，右侧为出口；箱体内部以0.09 m为间隔交错排列9列槽形挡板。入口处混合物颗粒体积浓度取10%，直径取0.165 mm；入口流速取2～6 m/s。此外为验证槽形挡板作用，设计另一套模型作为对比，取消了槽形挡板，其余尺寸和边界条件与原模型均相同。

计算结果表明槽形挡板在流速较高时有利于水—沙分离。分离效果以分离率衡量，即入口和出口颗粒流量的差值与入口颗粒流量的比值。两种模型(无挡板、有挡板)的分离率与入口流速的关系如图8所示。可以看出，入口流速2 m/s时，两者分离率相近，有挡板的分离率略低；随着入口流速增加，两者分离率均降低，但有挡板的分离效果优于无挡板，且作用越来越显著。以上现象的原因可能是：槽形挡板的存在一方面减小了流体可通过区域的横截面积而使流速升高，更易携带颗粒；另一方面在槽形挡板内部形成低速区，从而使进入该区域的颗粒失去动能进而沉降。当入口流速较低时，前者的影响超过后者；而当入口流速较高时，后者的影响超过前者。

图7 水—沙分离器模型(有挡板)Fig. 7 Water-sediment separator model (with baffles)

图8 两种模型的颗粒分离率与入口流速的关系Fig. 8 Relation between separation rate and inlet velocity

槽形挡板的分离效果除与流速有关外，还与其空间位置有关。选取入口流速为2 m/s和6 m/s的工况，以列为单位进行比较。每列挡板之间设置一纵截面，加上第1列前、第9列后、入口和出口附近，共12个纵截面，计算每个截面的颗粒流量；无挡板模型选取同样工况、同样截面位置进行比较。将每两个相邻截面颗粒流量之差，除以分离器入口与出口颗粒流量之差，称为局部分离率，用以衡量不同位置颗粒分离对总分离率的贡献，如图9所示。图中x表示截面距入口的距离。入口流速2 m/s时，无挡板的局部分离率在x=1.0 m之前差异不大，在x=1.0～1.2 m之间由于存在与流动方向垂直的壁面，颗粒与壁面碰撞后脱离主流，使得此处局部分离率升高；有挡板的局部分离率在第1列、第5列较高，在x=0～0.2 m和x=1.0～1.2 m区段局部分离率均低于无挡板情况。入口流速6 m/s时，两种模型局部分离率的空间规律更加显著：无挡板的局部分离率仍是在x=1.0 m之前变化较小，在x=1.0～1.2 m之间明显升高；有挡板的局部分离率在第1列最高，说明第1列挡板发挥的作用最大，其次在第5列、第9列亦呈现峰值。

图9 不同截面颗粒流量与局部分离率Fig. 9 Particle flow rate and local separation rate of sections parallel to inlet plane

通过观察分离器内的流线及颗粒浓度分布分析以上规律的原因。图10表示分离器内的流线在水平方向的投影，可以看出：尽管入口流速不同但流线的分布特征相似。流线在遭遇第1列槽形挡板后，一部分沿挡板内壁旋转；一部分被挡板阻碍，流向箱体角落；其余大部分则由挡板之间穿过，并向壁面延伸形成一Y字形高速区域，其末端被第5列最外侧两挡板阻碍；第5列挡板以后的流线分布趋于均匀。图11表示分离器内一具有代表性的水平截面的颗粒体积浓度分布。由图11可见，颗粒浓度分布与流线的分布有相似特征，呈现出一浓度较高的Y字形区域和一均匀分布的区域；第1列中部挡板与第5列外侧挡板(Y字形末端)颗粒浓度较高，推测此处颗粒沉降更加显著，因此颗粒的局部分离率较高。

图10 水—沙分离器流线水平方向投影Fig. 10 Streamlines in water-sediment separator

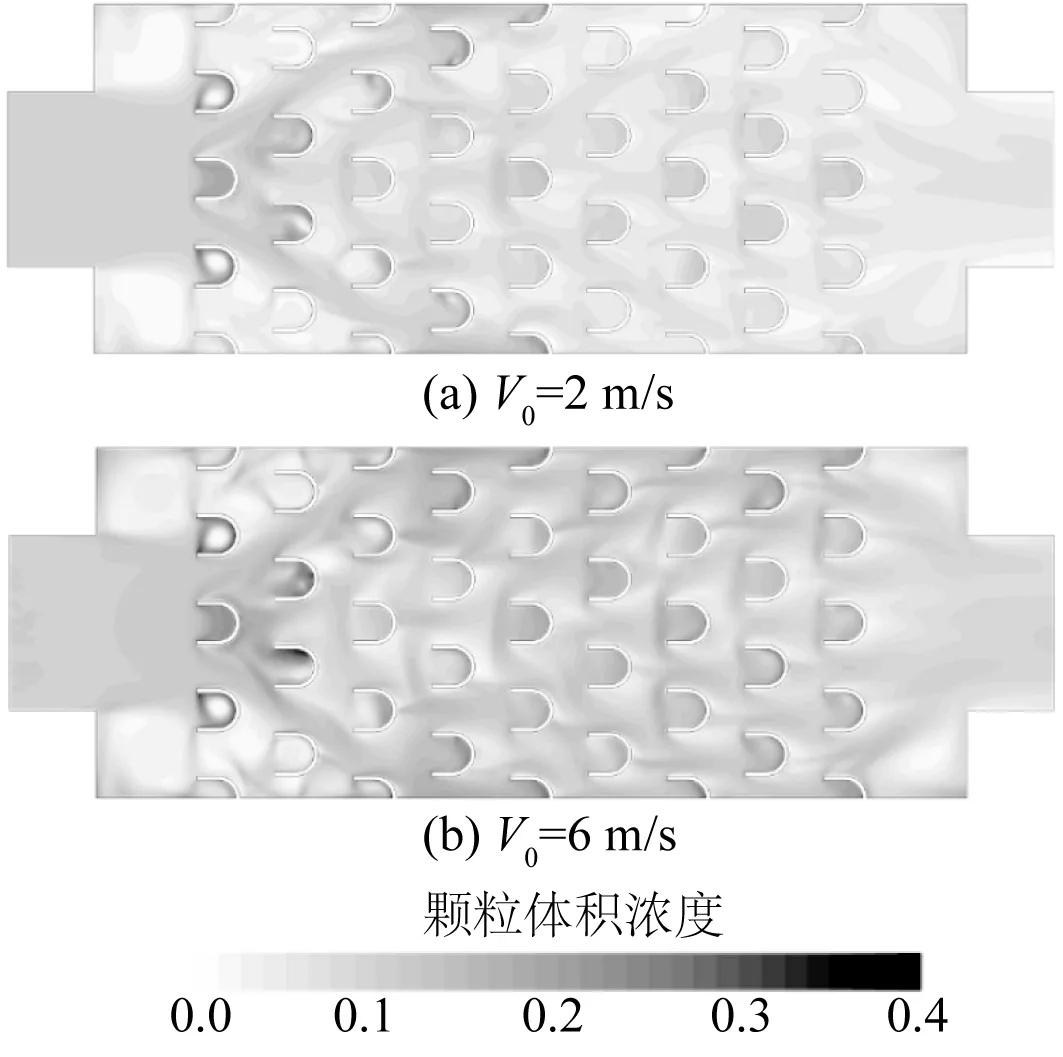
图11 水—沙分离器水平截面颗粒体积浓度分布Fig. 11 Distribution of particle volume concentration

水—沙分离器的阻力亦是衡量其特性的重要指标，主要是由流动分离造成的压差阻力，因此阻力特征采用入口平均压力与出口平均压力的差值表征，其与入口流速关系如图12所示。随着入口流速增大，分离器阻力显著增大；入口流速6 m/s时有挡板的阻力是无挡板的5倍。无挡板时，流动分离主要发生于箱体与出口管道相接处以及箱体各角落；有挡板时，在每个挡板的前后均会发生流动分离，流速越高则压差阻力越大，同时流体与挡板间的摩擦阻力亦会随流速升高而增大；此外，挡板所造成的阻力还与挡板的数量、尺寸、形状等要素相关。因此可通过优化上述设计变量，并选取适当的入口流速，从而在分离效果与功耗之间取得平衡。

图12 水—沙分离器阻力特征Fig. 12 Resistance of water-sediment separator

4 结 语

设计了一种用于深海采矿的循环式水力集矿系统，采用基于欧拉法的液固两相流模型，对该系统中的核心构件，即矿—沙分离器和水—沙分离器进行数值研究。结果表明：矿—沙分离器的效果与入口流速有关，入口流速大于0.6 m/s时具有较好的分离效果。水—沙分离器的效果亦受入口流速影响，低流速时分离率较高，高流速时槽形挡板可发挥作用，其局部分离率呈现一定的空间规律。水—沙分离器的阻力随流速增加而显著增加。可通过优化槽形挡板的几何参数和布置方式提升分离效果并降低阻力。上述方案可实现海底集矿系统中矿物与泥沙颗粒的有效分离，从而提高集矿效率，同时降低对海底环境的影响。