交错阵列甚低频信号产生方法研究
2020-10-24崔岸婧李道京
崔岸婧 李道京 周 凯 王 宇 洪 峻
①(中国科学院空天信息创新研究院微波成像技术重点实验室 北京 100190)
②(中国科学院大学 北京 100049)
③(西安电子科技大学电子工程学院 西安 710126)
1 引言
10 kHz量级甚低频电磁波信号具有较强的地物穿透能力,可用于地质勘探[1–3]。传统天线的辐射单元尺寸需达到1/4波长,否则不能有效辐射电磁波。频率为10 kHz电磁波信号的波长为30 km,其天线辐射单元尺寸在7~8 km,天线尺寸在10 km量级,这使其应用受到限制,研究基于适当尺寸高频雷达天线的甚低频电磁波信号产生方法具有重要意义。
甚低频电磁波信号产生一直是个难题,近年国外提出了一种采用机械旋转永磁体[4,5]的方式实现小型甚低频发射天线方法。该方法将机械能转换为电能,利用永磁体机械旋转直接激励电磁波,可突破天线物理尺寸限制。由于该方法涉及多学科交叉,国内外对该方法的研究均处于起步阶段,其性能尚未验证。
在文献[6]的基础上,本文将电磁波多普勒效应与交错阵列结合,通过对交错阵列中各辐射单元信号的波形、时序、相位和周期,以及阵列数等参数的控制,提出了一种在目标区合成甚低频信号的方法。该甚低频信号与地物相互作用后,可通过磁探仪[7]接收处理,用于地质分析。
2 电磁波多普勒效应
文献[8–11]推导了电磁波多普勒效应的原理。以运动雷达为信号源,接收装置位于目标区,二者均位于静止坐标系K中,初始坐标分别为(R0,0,0)和(0,0,0)。以雷达为原点建立运动坐标系K′,且在运动过程中,雷达始终位于K′系原点,K′系与K系的时间关系符合钟慢效应[12]。记K′系中雷达发射信号的频率为f0,由雷达运动所产生的多普勒频率为fd,K系中接收信号频率为f0r。如图1所示,左侧为接收装置,右侧为雷达与运动坐标系K′。雷达在K系中以速度v沿x轴正方向远离接收装置运动,且在运动过程中,K′系的x′轴与K系的x轴始终重合。
以下推导电磁波多普勒效应中脉宽与频率的变化[13]。设雷达发射信号在K′系中的脉宽为τeK′,在K系中的对应脉宽为τeK,K系中接收信号的脉宽为τrK,其中τeK′和τrK的关系符合常见的电磁波多普勒效应,信号频率的变化也由τeK′和τrK推导,τeK和τrK的关系表示K系中信号脉宽的变化。
由多普勒效应,当雷达远离目标运动时,K系中接收信号脉宽τrK与K′系中发射信号脉宽τeK′的关系为
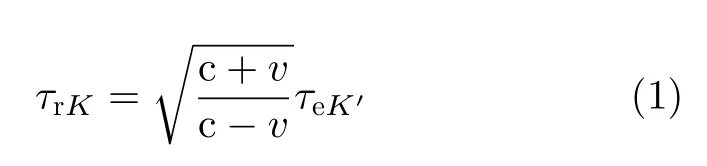
其中,v为雷达运动速度,c为光速。由钟慢效应,雷达发射信号在K系与K′系中脉宽的对应关系为
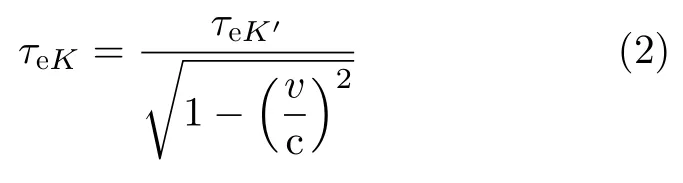
将式(2)代入式(1)可得K系中雷达发射信号与目标处接收信号脉宽的关系
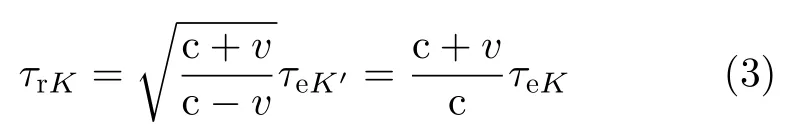
因此雷达发射信号在K′系和K系中的脉宽展宽量为分别为
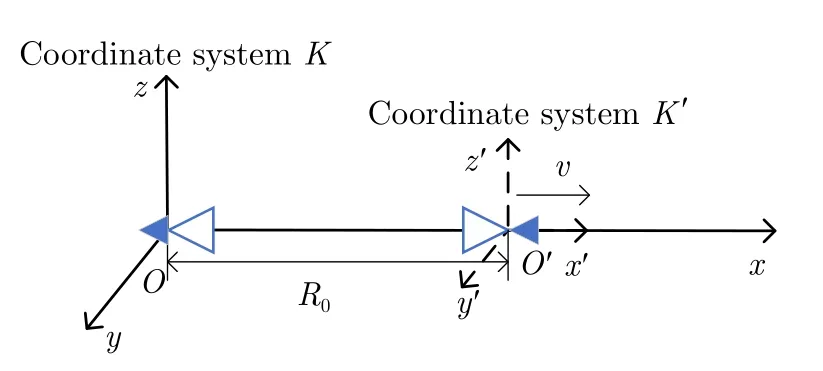
图1 雷达运动示意图Fig.1 Radar motion diagram
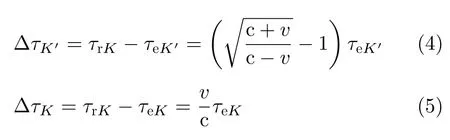
式(5)表示静止坐标系K中雷达发射信号脉宽变化。
由于K′系中发射信号与K系中接收信号脉冲中信号的周期数不变,因此信号频率变化由K′系中雷达发射信号脉宽和K系中接收信号脉宽可得
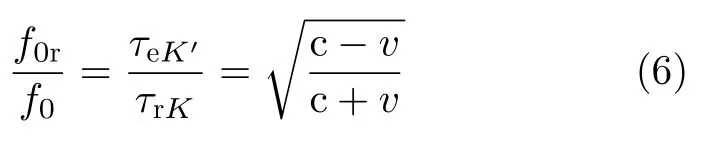
对应的多普勒频率为
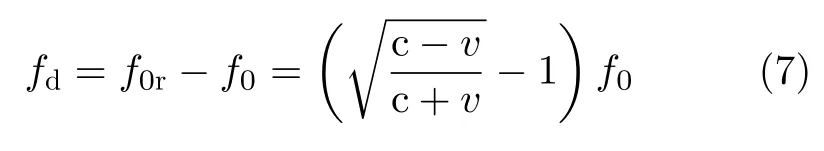
当雷达远离目标运动的速度接近电磁波速度c时,接收信号频率将会明显降低。
若雷达与目标的初始距离为30 km,发射载频100 MHz脉宽为0.05 µs的信号,同时以速度v远离目标运动,多普勒频率为–99.99 MHz,目标区接收信号频率为10 kHz,脉宽为500 µs,雷达发射信号与目标区接收信号的波形和频谱如图2所示。
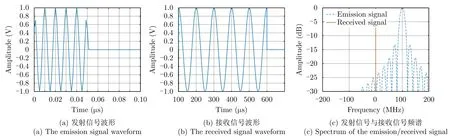
图2 多普勒效应中的发射/接收信号波形与频谱Fig.2 The emission/received signal waveform and spectrum of Doppler effect
3 交错阵列甚低频信号产生方法
3.1 甚低频信号产生原理
根据对电磁波多普勒效应的理解,如图3(a)所示,在图1的基础上,在静止坐标系中分解运动雷达发射信号的过程。图中的x轴为静止坐标系K的x轴,t轴表示雷达运动的时间,设雷达在t0时刻位于xR0处,并从该时刻开始在K系中以速度v沿x轴正方向运动并发射信号。以时间间隔 ∆t将雷达的运动过程进行分解,则每个时间间隔内雷达的运动距离为v∆t,此时雷达运动过程变为步进过程。如图3(b)所示,用天线阵列近似步进的雷达运动过程,天线阵列和接收装置均位于K系中。
采用多行阵列构成交错阵列,可缩短辐射单元间距,减小离散化的时间间隔,使得合成信号更接近所需的低频信号。如图4所示,在直角坐标系中建立交错阵列结构。Nl行阵列在xoz平面内错位排布,单行阵列沿x轴负方向排布,相邻阵列在x轴以距离ds错位,沿z轴正方向以间距hλ/2排布,λ为辐射单元信号的载波波长。单行阵列的阵长为L0,辐射单元间距d0λ/2,辐射单元个数N0。接收装置位于目标区,目标位于45°扫描角[14,15]方向,坐标为(x0,y0,0),与阵列近端距离为R0。当单行阵列辐射单元间距d0为错位距离ds的Nl倍时,由于h ≪R0,阵列在z轴上的距离影响极小,所以Nl行阵列等效在x轴构成辐射单元间距ds、阵长为LsL0+(Nl−1)ds的交错阵列。
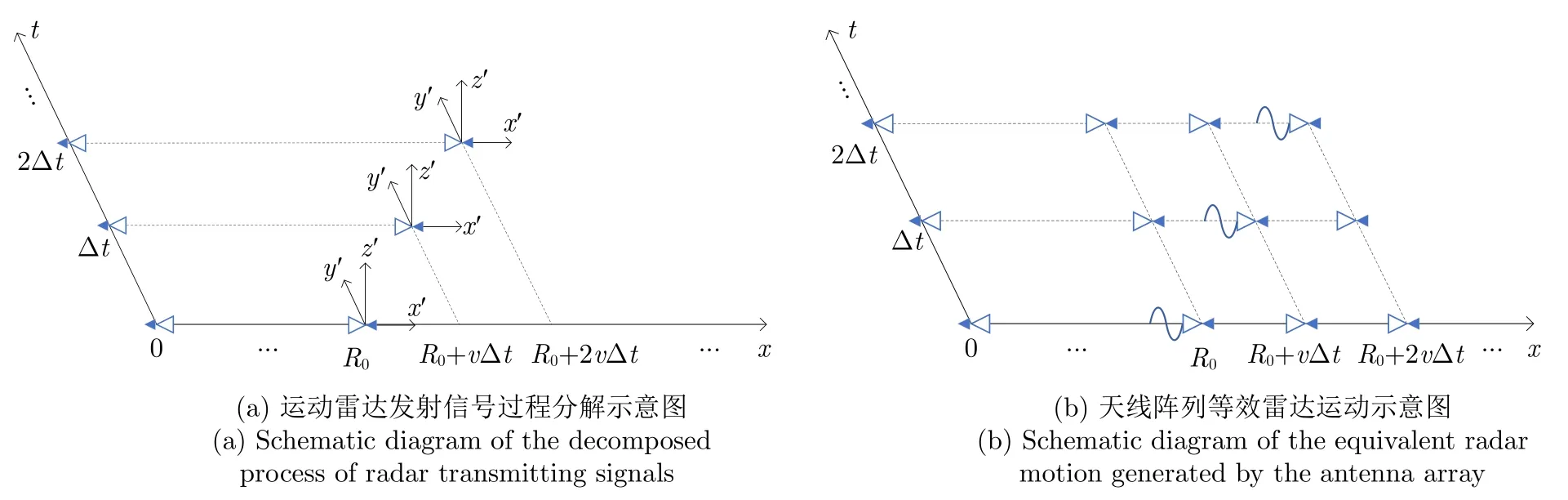
图3 运动雷达发射信号过程分解和天线阵列等效雷达运动示意图Fig.3 Schematic diagram of the decomposed process of radar transmitting signals and the equivalent radar motion generated by the antenna array
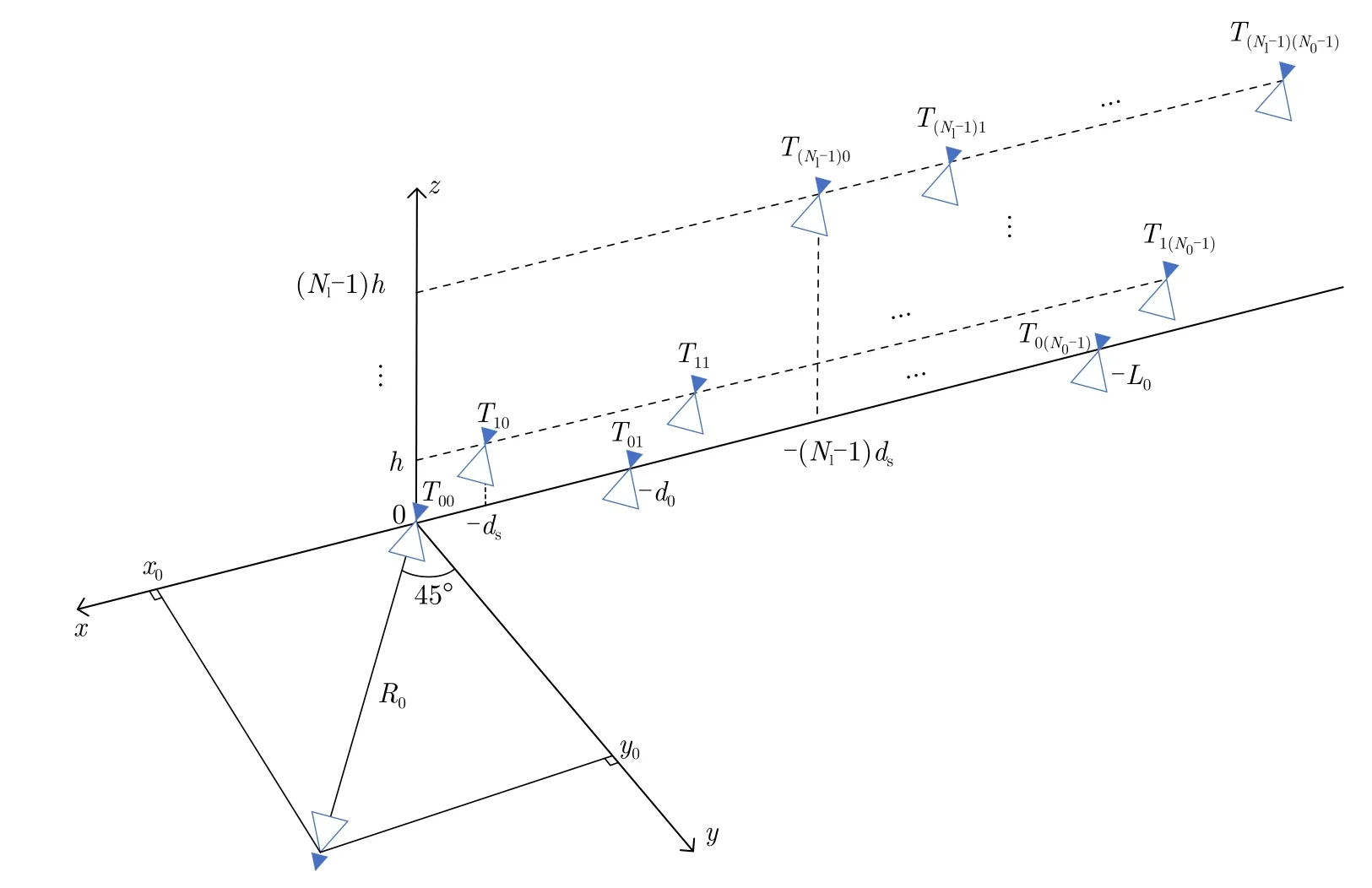
图4 交错阵列结构Fig.4 Staggered array structure
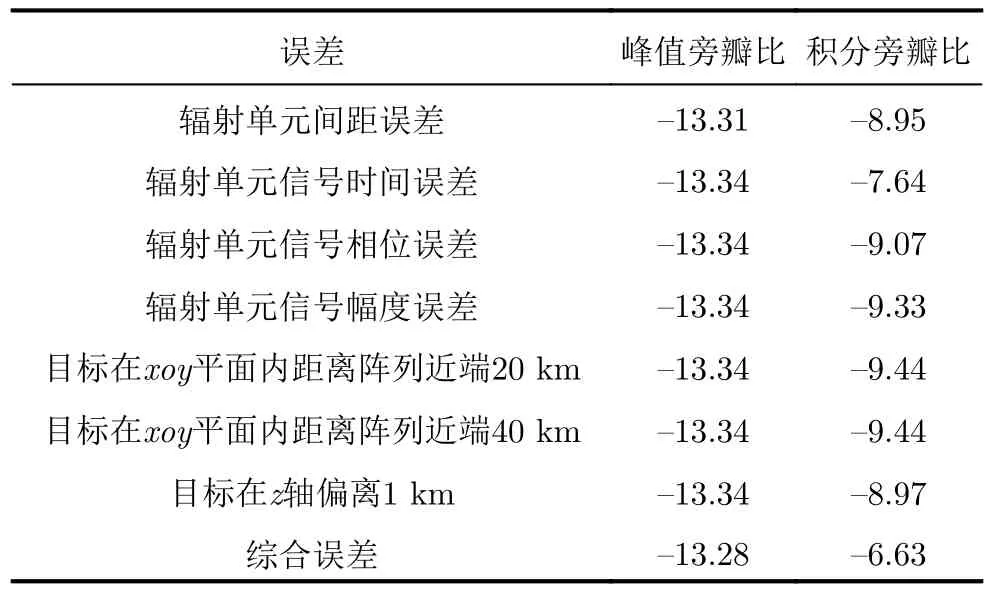
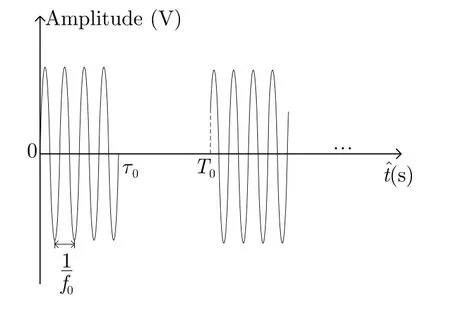
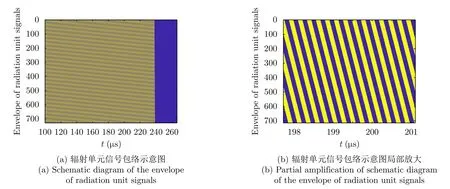
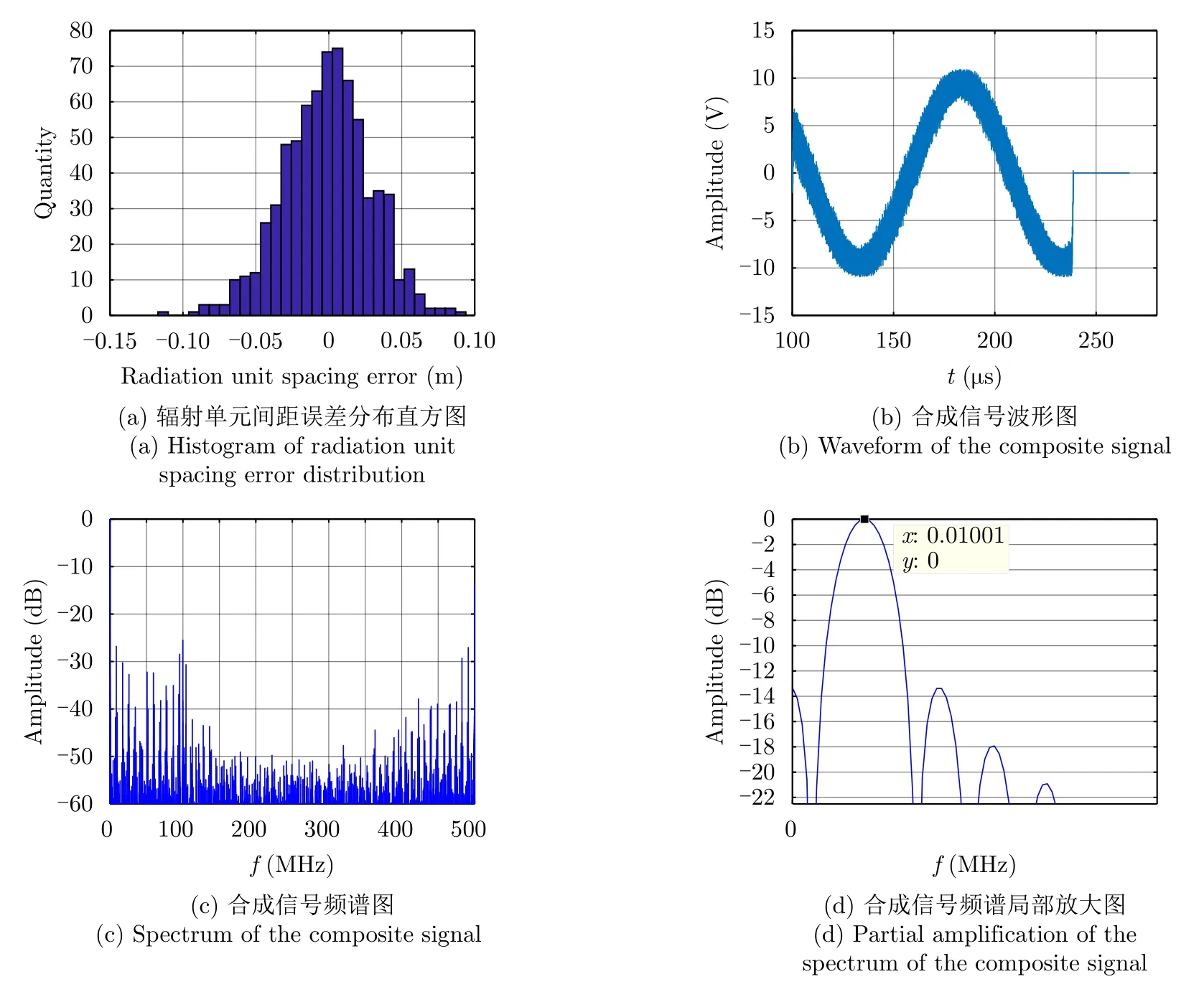
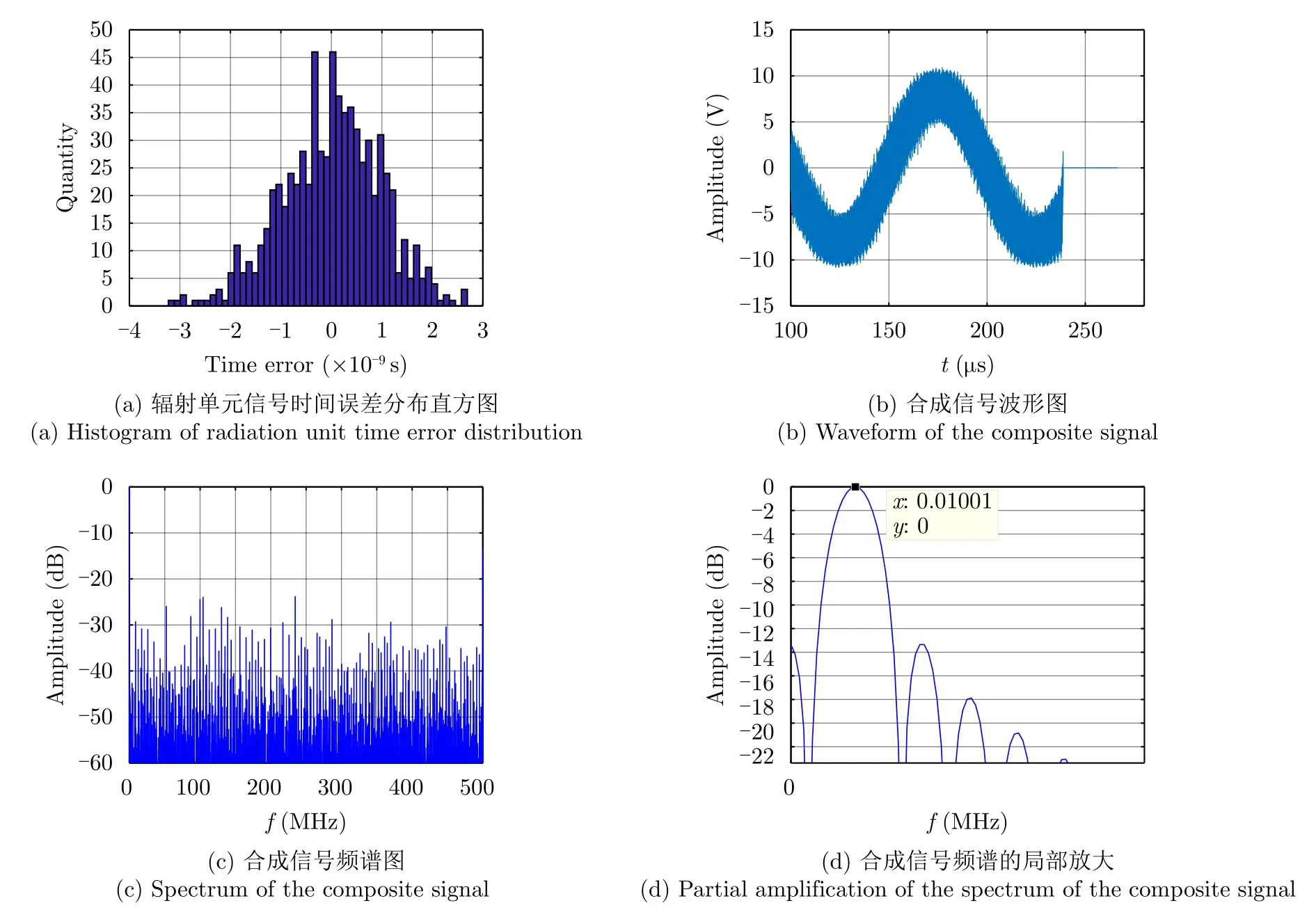
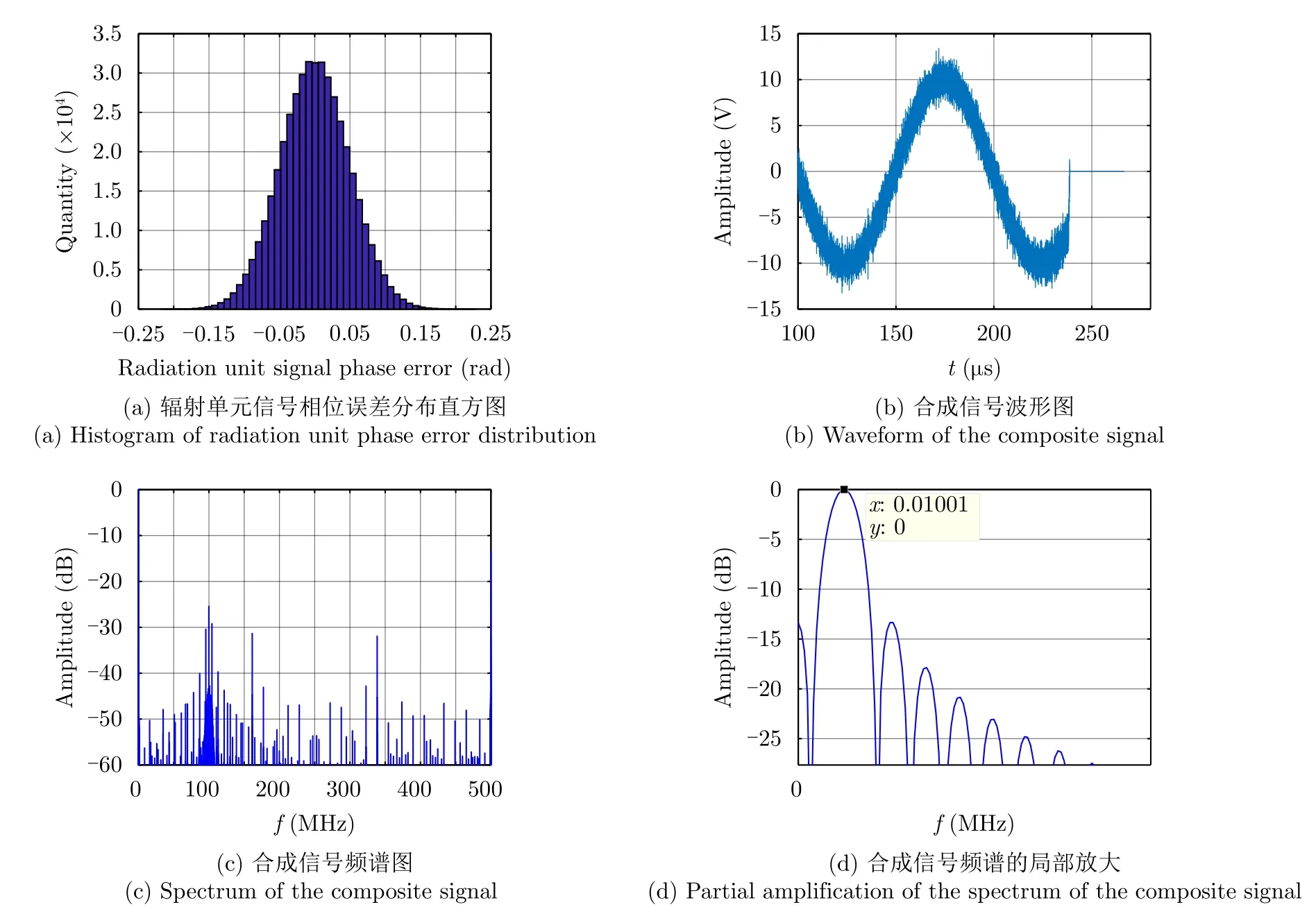
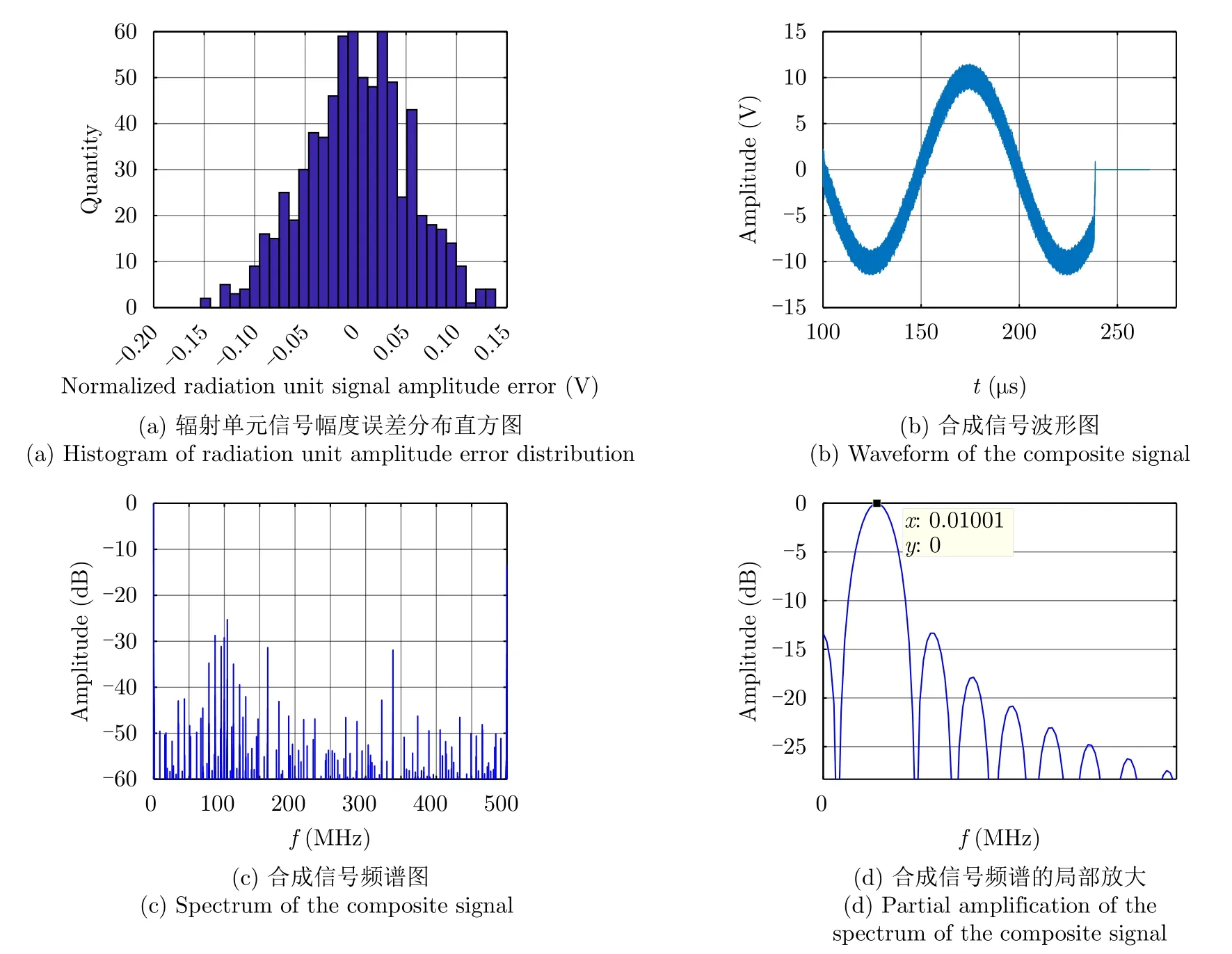
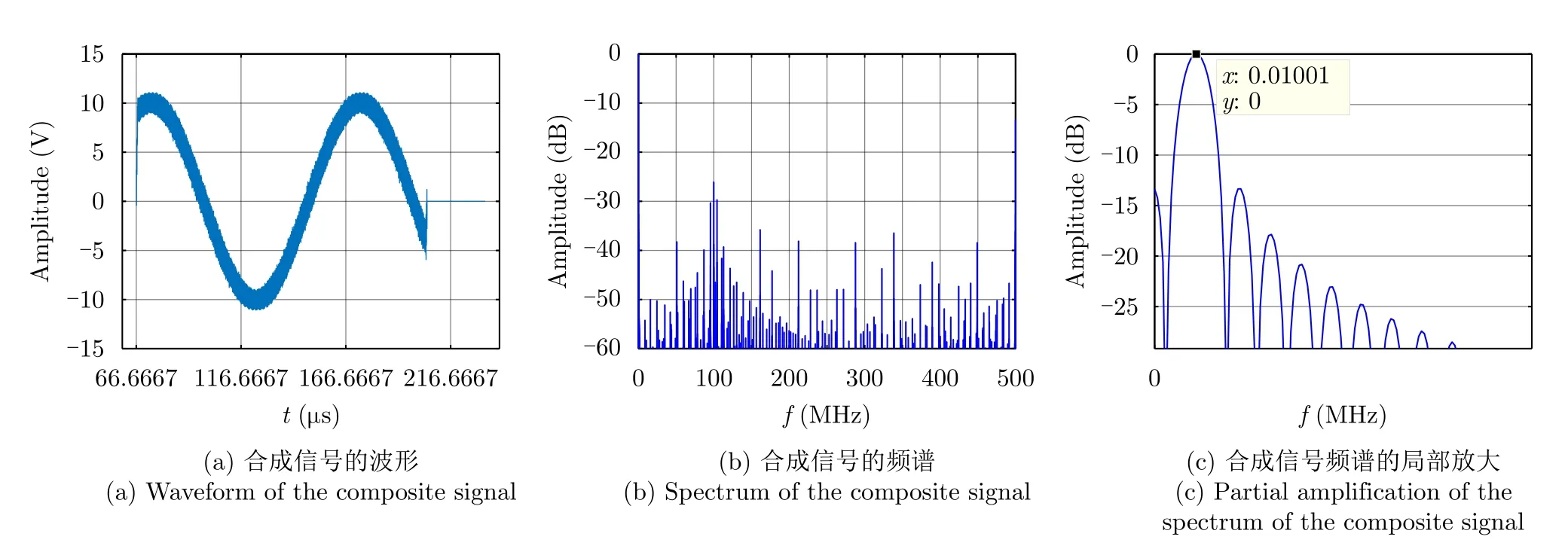
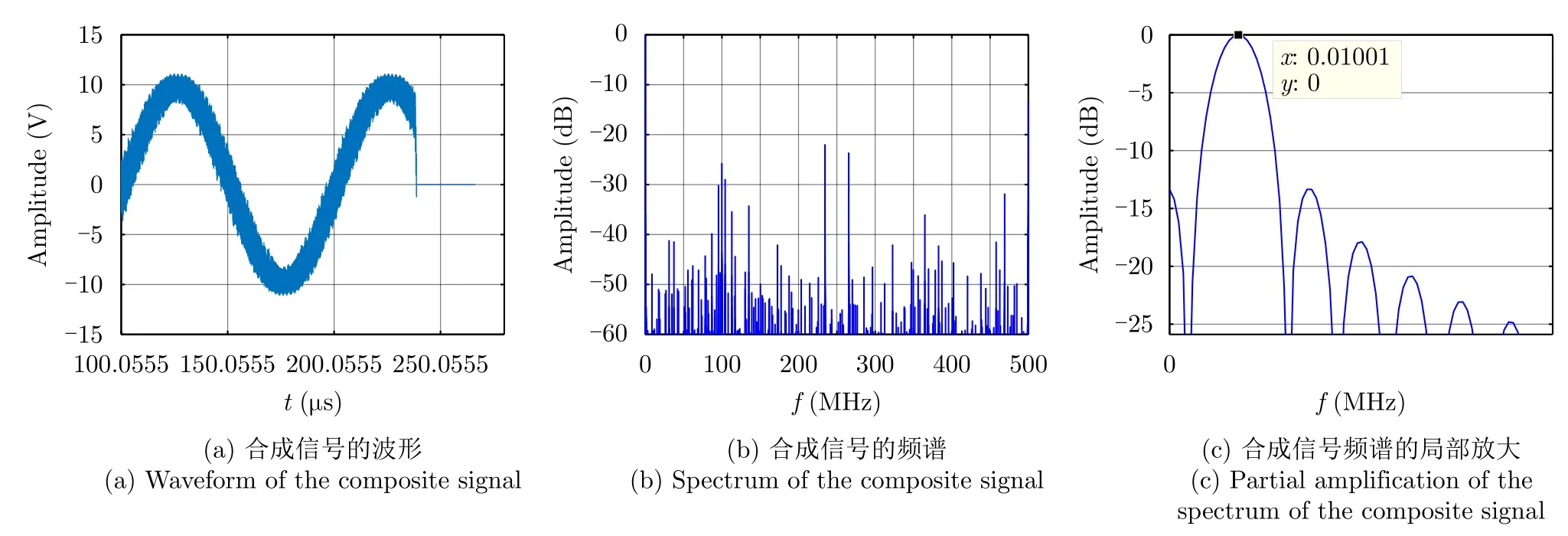
辐射单元记为Tnln0,其中nl和n0分别表示该辐射单元所在的阵列与阵列中的位置(nl0,1,···,Nl−1;n00,1,···,N0−1)。通过交错阵列中近端至远端的辐射单元依次发射信号,等效雷达在阵列上的高速运动。单行阵列与交错阵列中,辐射单元发射信号的时间间隔分别为d0/v和ds/v,0≤v 3.2.1 辐射单元信号波形及其参数选择 (1) 辐射单元信号波形阵长产生的辐射单元信号脉宽展宽量为 令辐射单元信号脉宽等于雷达发射信号在K系中的脉宽τeK,∆τL等效多普勒效应中信号脉宽展宽量∆τK。由式(5),当v →c时,∆τK ≈τeK,即辐射单元信号脉宽与其展宽量近似相等,因此当辐射单元发射单脉冲信号时,目标区合成信号的脉宽为 为获得甚低频信号,合成信号需要有足够大的脉宽。在阵长固定的条件下,直接增大辐射单元信号脉宽将导致合成信号中载波频率分量的增大,影响甚低频信号对阵列发射信号的能量利用率。 为增大合成信号的脉宽,令辐射单元发射周期脉冲串信号,通过增加辐射单元信号的周期数实现合成信号脉宽的增大。利用阵列产生的脉宽展宽量填补周期脉冲串信号的休止期,使得目标区合成信号在其时宽内连续。辐射单元信号波形如图5所示。辐射单元信号周期和脉宽分别记为T0和τ0,3.2.2节中将推导T0和τ0的取值。辐射单元信号每个脉冲前沿的相位根据多普勒效应设置。每个辐射单元信号脉冲内包含多个辐射单元信号载波周期1/f0。 用快时间和慢时间描述辐射单元信号与目标区的合成信号。记同一辐射单元信号的时间为快时间ˆt,不同辐射单元信号的时间为慢时间tm,目标区信号的时间为tr,三者之间的关系为 (2) 辐射单元信号脉宽与周期 图5 辐射单元信号示意图Fig.5 Schematic diagram of the radiation unit signal 由式(8)可得阵列产生的脉宽展宽量∆τL。根据式(5),当vc时,静止坐标系K中雷达发射信号脉宽与其脉宽展宽量相等,即τeK∆τK,此时τeK占接收信号脉宽τrK的50%。令辐射单元信号脉宽τ0、周期T0和阵列产生的脉宽展宽量∆τL分别等效τeK,τrK与∆τK。由于合成甚低频信号的仿真中v →c,则有τ0≈∆τL,τ0≈,因此将辐射单元发射的周期脉冲串信号的占空比选定为50%,辐射单元信号脉宽为 辐射单元信号周期为 此时∆τL恰好填补辐射单元信号的休止期,目标区合成信号的时间连续。 若将辐射单元信号周期减小为 其中u>1,此时辐射单元信号的休止期∆τL,因此阵列产生的脉宽展宽量能够实现周期脉冲串信号休止期的填补,使得目标区合成信号的时间连续。 通过增大u,减小辐射单元信号周期,增加辐射单元信号周期数,等效增加合成信号相位调制次数,实现谐波的抑制,同时减少叠加所导致的信号抵消,提高合成信号对阵列发射信号的能量利用率。4.1节中仿真分析了辐射单元信号周期对目标区合成信号性能的影响。 (3) 合成信号脉宽 合成信号由交错阵列中各辐射单元发射的周期脉冲串信号构成。记各辐射单元发射周期脉冲串信号的周期数为Np,合成信号脉宽为 其中第1项为各辐射单元发射信号的时长,第2项为交错阵列近端与远端辐射单元信号传播至目标区的时间差。 3.2.2 辐射单元信号与目标区合成信号表达式 由多普勒频率与辐射单元斜距可得辐射单元信号[16]和目标区合成信号表达式。辐射单元与目标之间的距离为 由式(6)和式(15),可得辐射单元信号的表达式 目标区的合成信号等于交错阵列中各辐射单元信号的叠加,因此目标区合成信号的表达式为 由于辐射单元信号仅设置各脉冲的初始相位,脉冲内没有相位调制,因此辐射单元信号属于窄带信号,可有效辐射。增大辐射单元的带宽有益于保证合成信号的性能。 若假设辐射单元带宽为中心频率的10%,为保证辐射单元信号带宽满足要求,限制辐射单元信号的周期与脉宽 即辐射单元信号周期与脉宽的最小值分别为20/f0和10/f0。 结合实现空间加密的交错阵列结构和设置确定相位的辐射单元信号,使得合成信号相位在快时间上快速变化,带宽有限的辐射单元信号在空间构成宽谱的合成信号。 (1) 辐射单元信号周期 图6 辐射单元信号周期为T0/2时合成信号的波形、频谱与频谱对比图Fig.6 Waveform,spectrum and spectral contrast diagram of the composite signal when the radiation unit signal period being T0/2 以下利用峰值旁瓣比(Peak Side Lobe Ratio,PSLR)、积分旁瓣比(Integrated Side Lobe Ratio,ISLR)[17]和发射信号能量利用率评价合成信号中谐波分量的影响。 因为各辐射单元信号的形式相同,所以可用辐射单元T00的信号等效其他辐射单元信号,由此可得交错阵列的发射信号。将归一化处理的阵列发射信号频谱和合成信号频谱进行对比,可分析发射信号的能量利用率。 当目标位于xoy平面内且距离阵列近端30 km,辐射单元信号载波频率为100 MHz,单行阵列长度为120 m,交错阵列由5行阵列构成,其长度为121.2 m,单行阵列与交错阵列中辐射单元间距分别为1.5 m和0.3 m,辐射单元数分别为81和405,合成信号频率10 kHz时,分别仿真辐射单元周期为T0/2和T0/6的情况下,合成信号的波形、频率与频谱对比图,仿真结果如图6、图7和表1所示。根据交错阵列阵长,可得辐射单元信号最大周期T0=1.38 µs。仿真中描述信号的采样频率为500 MHz(对应时间分辨率为2 ns),通过多行阵列交错排布,减少辐射单元间隔,实现空间加密,降低系统对时间分辨率的要求,提高该采样频率有助于对合成信号的描述。 图7 辐射单元信号周期为T0/6时合成信号的波形、频谱与频谱对比图Fig.7 Waveform,spectrum and spectral contrast diagram of the composite signal when the radiation unit signal period being T0/6 表1 辐射单元信号周期取T0/2和 T0/6时的仿真参数与结果Tab.1 Simulation parameters and results when the radiation unit signal period being T0/2 and T0/6 respectively 对比图6、图7及其表1中的仿真结果可见,通过减小辐射单元信号周期,可抑制谐波和载波分量,减少由叠加导致的信号抵消,提高交错阵列发射信号能量的利用率。由于通常辐射单元带宽为中心频率的10%,为保证辐射单元信号脉宽满足要求,不再增大u或减小辐射单元信号周期。 (2) 交错阵列行数和等效辐射单元间距 当辐射单元信号周期取T0/6=0.23 µs时,根据表1所示参数,仿真9行阵列构成的交错阵列在目标区合成信号的波形、频谱与频谱对比图。仿真结果如图8所示。 图8中合成信号频谱的峰值旁瓣比为–13.34 dB,积分旁瓣比为–9.44 dB,低频信号在合成信号中的能量占比为89.79%。频谱对比图中,随机相位辐射单元信号所合成信号的频率分量分布于辐射单元信号载频附近,而当辐射单元信号相位根据多普勒效应设置时,其合成信号的10 kHz分量幅度为–2.542 dB,对应的发射信号能量利用率为74.63%。 图8 辐射单元信号周期为T0/6时9行阵列构成的交错阵列在目标区合成信号的波形、频谱与频谱对比图Fig.8 Waveform,spectrum and spectral contrast diagram of the composite signal generated by the 9-row staggered array when the radiation unit signal period being T0/6 对比图7和图8,通过多行阵列交错排布的方式减小辐射单元间距,可在步进方式下更精确模拟高速运动多普勒信号,抑制合成信号的谐波,并提高发射信号的能量利用率。 上述信号产生过程中,信号包络也在同步移动,如图9所示,这与雷达成像[18]中的距离徙动类似。由于多普勒效应涉及频率的变化,所以本文甚低频信号产生过程已不属于线性过程。 分析辐射单元间距误差、辐射单元信号的时间、相位、幅度误差以及目标偏离预定位置对合成信号的影响,对实际应用具有意义。以下对合成信号的误差分析基于9行阵列构成交错阵列、辐射单元周期为T0/6的前提。 (1) 辐射单元间距误差 当辐射单元间距误差服从均值为0,标准差为0.03 m的正态分布时,误差的分布、目标区合成信号的波形与频谱如图10所示。 (2) 辐射单元信号时间误差 当辐射单元信号时间误差服从均值为0,标准差为1 ns的正态分布时,误差的分布、目标区合成信号的波形与频谱如图11所示。 (3) 辐射单元信号相位误差 当辐射单元信号相位误差服从均值为0,标准差π/26的正态分布时,相位误差分布、目标区合成信号的波形与频谱如图12所示。 (4) 辐射单元信号幅度误差 辐射单元增益的不同将导致辐射单元信号的幅度误差。当归一化电压幅度误差服从均值为0,标准差为0.05 V的正态分布时,对误差分布与合成信号的仿真如图13所示。 (5) 目标偏离预定位置 以上仿真中,目标均位于xoy平面内45°扫描角方向,与交错阵列近端距离30 km。若目标偏离该预定位置,将对合成信号产生影响。 图9 辐射单元信号包络示意图Fig.9 Schematic diagram of the envelope of radiation unit signals 图10 辐射单元间距误差分布、目标区合成信号的波形与频谱图Fig.10 The distribution of spacing error,waveform and spectrum of the composite signal in target area 当目标位于xoy平面内45°扫描角方向,与交错阵列近端距离20 km和40 km时,合成信号的波形与频谱如图14和图15所示。 若目标在xoy平面上的投影为预定位置,在z轴上偏离1 km,由式(14)可得各辐射单元信号传播至实际目标区的慢时间为 其中z0=1 km。由于辐射单元在z轴上的位置znlh对(z0−nlh)2有较大影响,因此当目标不在xoy平面内时,辐射单元在z轴上的排布不可忽略,仿真结果如图16所示。 图11 辐射单元信号时间误差分布、目标区合成信号的波形与频谱图Fig.11 The distribution of radiation unit signal time error,waveform and spectrum of the composite signal in target area 图12 辐射单元信号相位误差分布、目标区合成信号的波形与频谱图Fig.12 The distribution of radiation unit signal phase error,waveform and spectrum of the composite signal in target area 图13 辐射单元信号幅度误差分布、目标区合成信号的波形与频谱图Fig.13 The distribution of radiation unit signal amplitude error,waveform and spectrum of the composite signal in target area 图14 目标在xoy平面内45°扫描角方向距离阵列近端20 km时目标区合成信号的波形与频谱Fig.14 Waveform and spectrum of the composite signal in the target area when the target is 20 km away from the near end of the array at 45° scanning angle in xoy plane (6) 综合误差 当目标位于xoy平面内45°扫描方向,距离交错阵列近端40 km时,不考虑交错阵列在z轴上的排布影响,若交错阵列及其信号同时受到辐射单元间距误差、辐射单元信号相位和幅度误差,目标区合成信号的波形和频谱如图17所示。 (7) 仿真结果分析 表2给出了各误差影响下目标区合成信号频谱的峰值旁瓣比和积分旁瓣比。由仿真结果可见,辐射单元间距误差,辐射单元信号时间、相位、幅度误差和目标偏离预定位置均导致合成信号中谐波分量的增大,其中辐射单元信号时间误差和目标在z轴上偏离预定位置对合成信号的影响较大。 图15 目标在xoy平面内45°扫描角方向距离阵列近端40 km时目标区合成信号的波形与频谱Fig.15 Waveform and spectrum of the composite signal in the target area when the target is 40 km away from the near end of the array at 45° scanning angle in xoy plane 图16 目标沿z轴偏离1 km时目标区合成信号的波形与频谱Fig.16 Waveform and spectrum of the composite signal in the target area when the target deviates 1 km along the z-axis 图17 受综合误差影响时目标区合成信号的波形与频谱Fig.17 Waveform and spectrum of the composite signal in the target area influenced by synthetical error 结合电磁波多普勒效应和交错阵列,本文研究了高频天线在目标区合成甚低频信号的问题。将辐射单元信号设计为周期脉冲串信号,通过阵列产生的脉宽展宽量填补信号的休止期,使得合成信号时间连续。通过多行阵列交错排布减小辐射单元间隔,降低系统对时间分辨率的要求。从仿真结果看,本文提出的交错阵列甚低频信号产生方法具有一定的可行性。但合成信号的谐波控制水平和发射信号能量利用率仍待进一步提高。 表2 不同误差影响下合成信号频谱参数(dB)Tab.2 Spectrum parameters of the composite signal influenced by different errors (dB) 致谢 感谢西安电子科技大学的水鹏朗老师对本文工作的帮助。3.2 交错阵列信号及其参数选择
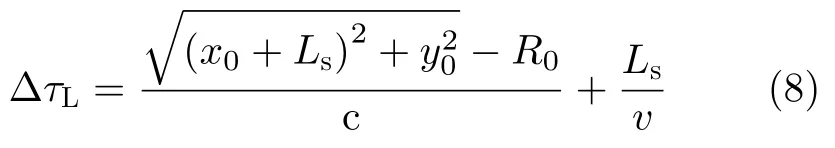
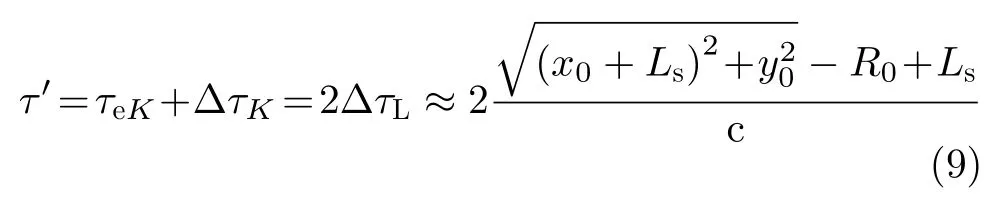

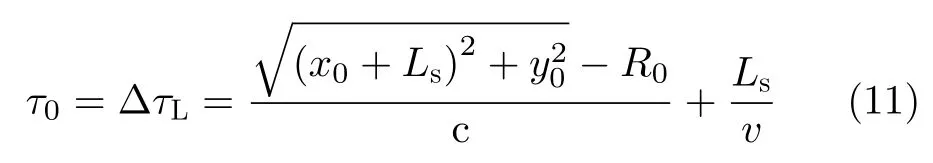
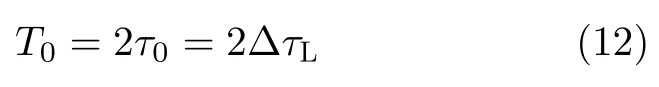

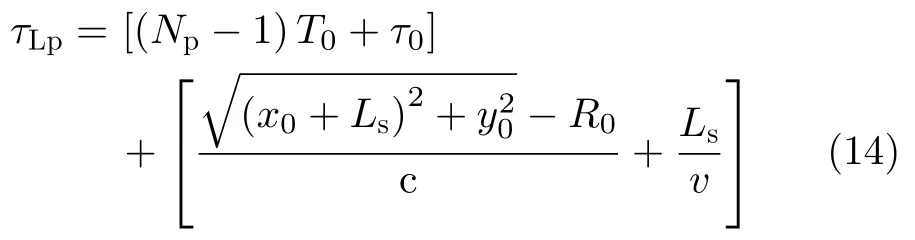


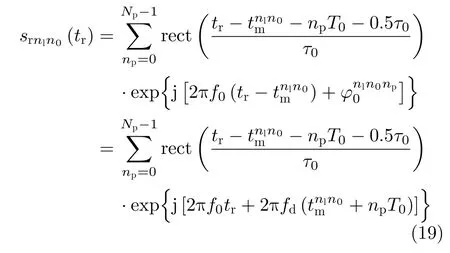
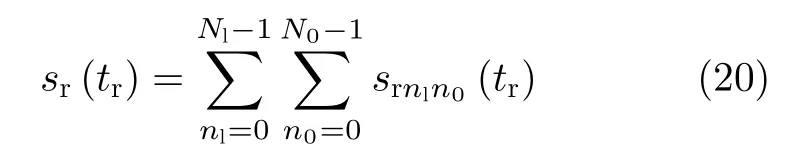
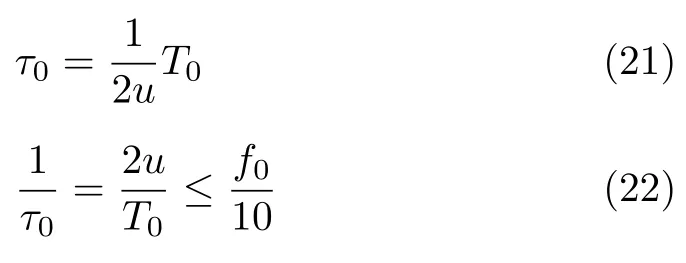
4 仿真分析
4.1 参数和能量利用率
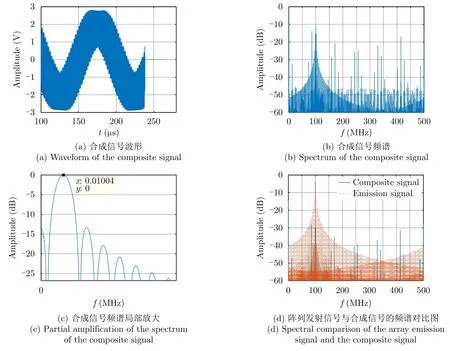
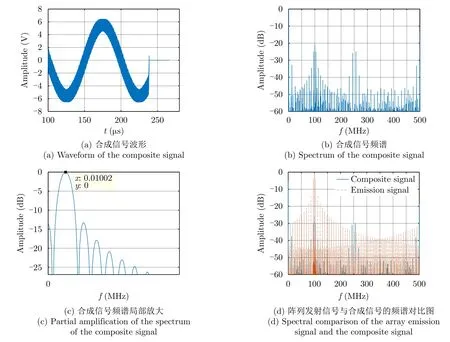
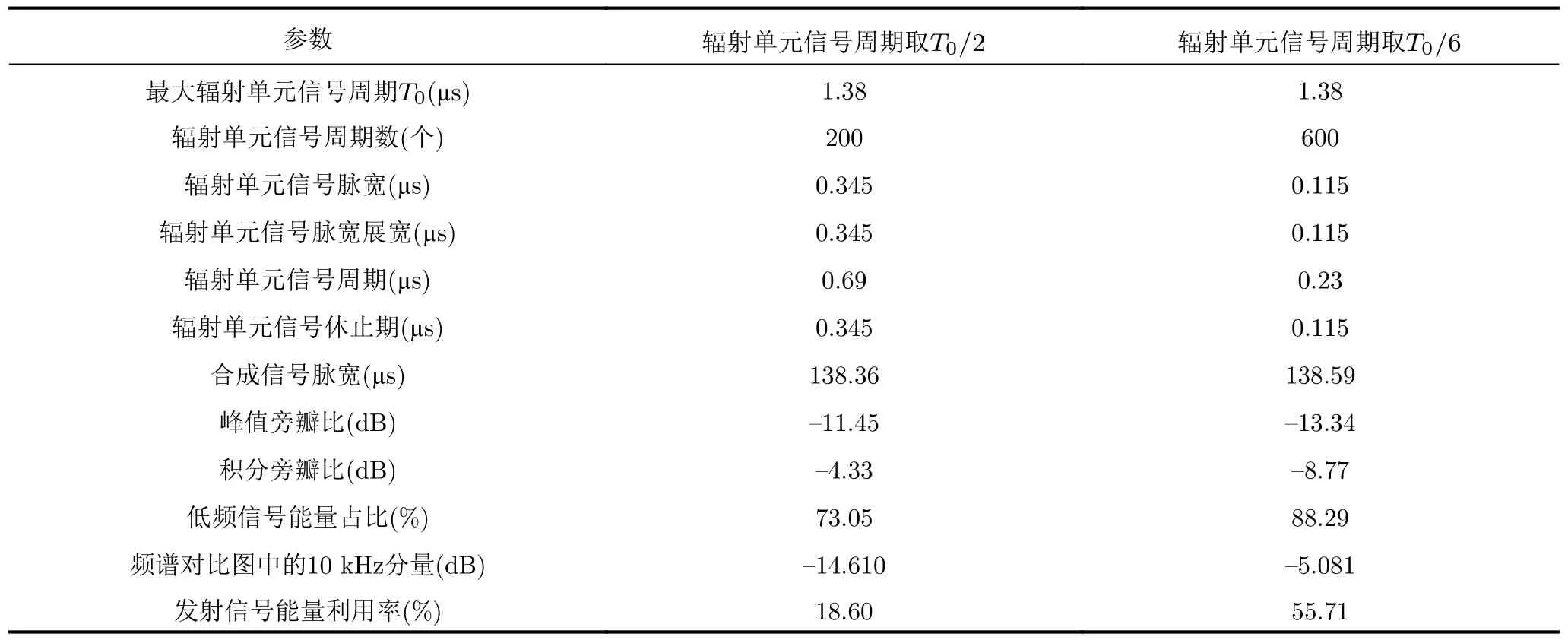
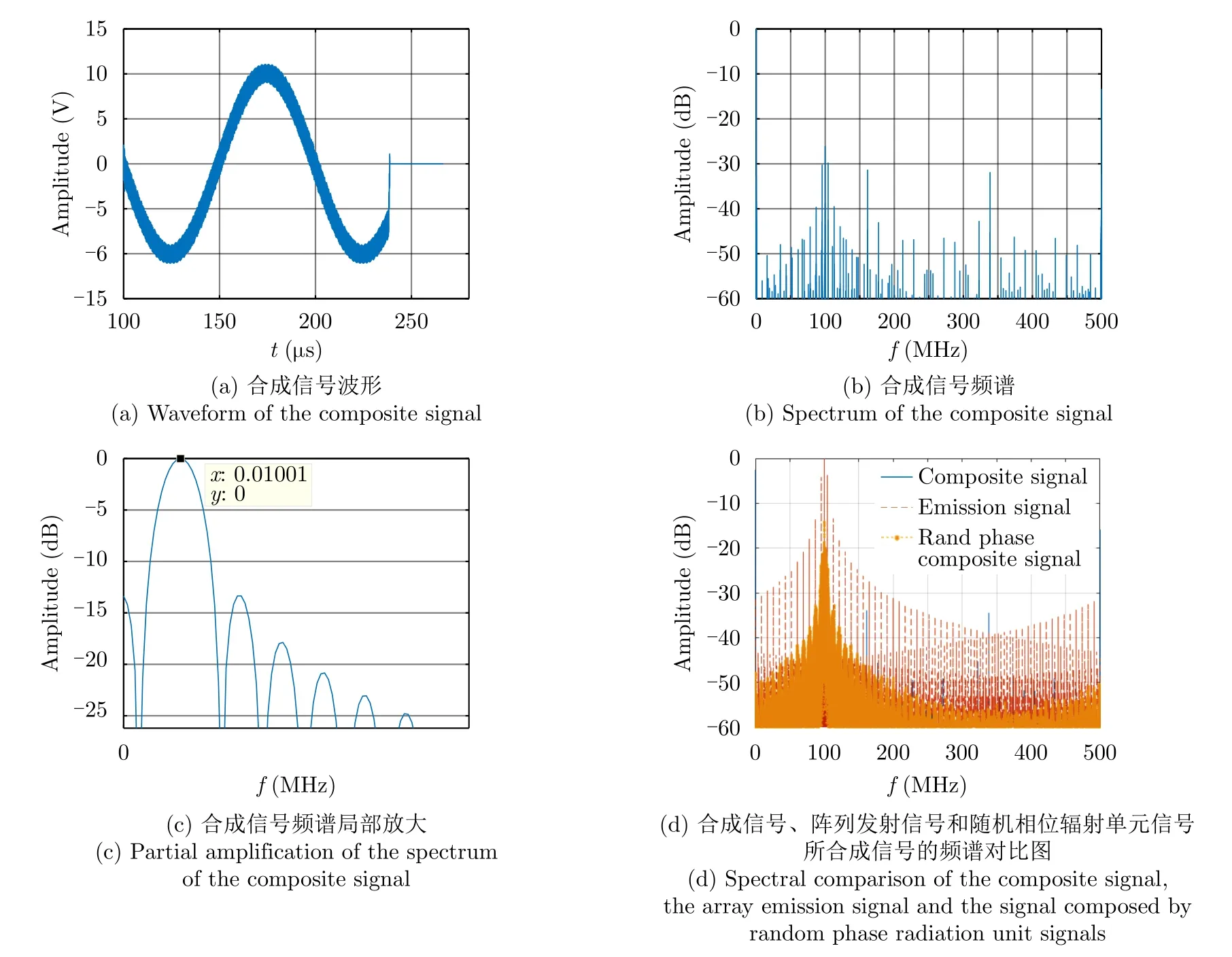
4.2 误差条件下的性能分析
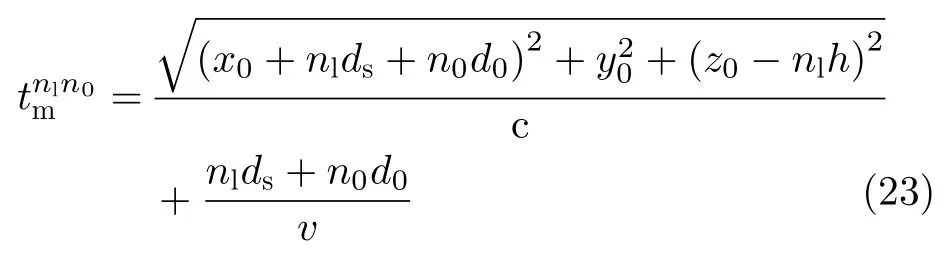
5 结束语