基于成像坐标系优化的中轨星载SAR成像方法

李 航 刘文康 孙光才 邢孟道 李光伟 费晓燕

①(西安电子科技大学雷达信号处理国家重点实验室 西安 710071)

②(西安电子科技大学信息感知技术协同创新中心 西安 710071)

1 引言

与目前的低地球轨道星载合成孔径雷达(Low-Earth-Orbit Synthetic Aperture Radar,LEO SAR)相比，中地球轨道星载合成孔径雷达(Medium-Earth-Orbit Synthetic Aperture Radar,MEO SAR)具有更大的幅宽；它的广域覆盖范围长达数百公里，重访时间短，只有几分钟，在许多领域中显示出巨大应用潜力。MEO SAR长时间观测目标区域，提供连续的SAR图像，有助于实现动态监视。利用多级带宽设计和波束扫描，MEO SAR可以工作在不同的模式，并实现灵活的分辨率和场景覆盖。

由于MEO SAR所在的中轨卫星与地球之间的相对运动较慢，在满足分辨率要求的情况下，合成孔径时间变得更长。而随着合成孔径时间的增加会出现一些问题，例如大气相位误差、斑点噪声等[1–3]。中地球轨道的轨迹曲率也可能影响波束驻留时间和等效卫星速度，从而导致分辨率和信号特性随轨道时间改变，因此波束指向控制对于中高轨曲线轨迹SAR具有重要的意义——能够调整和保持系统标称分辨率，波束扫描速率需要根据轨道位置、视角等进行设计。另外，对于大场景成像，MEO SAR信号方位平移不变性失效，此时回波信号是两维空变的[4,5]。

对于MEO SAR信号的两维空变问题，常规的成像算法将其分两维处理。一些成熟的距离空变校正方法，例如chirp scaling[6–8]和omega-K[9,10]算法，经过改进后，同样能用来有效处理弯曲轨迹的SAR数据。经过方位非线性变标[11–13]，重采样[14,15]等一些方位向预处理方法处理之后，信号能够满足方位平移不变性，但是这些方位空变校正处理会引入多次傅里叶变换或者插值操作，明显增加了成像算法的运算量。一些时域算法也适用于弯曲轨迹的星载SAR成像，例如BPAs[16,17]和FFBPAs[18–20]，这些基于时域插值的算法能够直接处理复杂的两维空变，是未来高分辨率、弯曲轨道星载SAR处理的一个潜在选择。通常，尽管频域算法需要一些额外的操作来获得方位平移不变性，但它们的计算复杂度通常小于时域算法。

本文为条带模式下的MEO SAR数据的两维空变处理提出了一种有效的处理方法。基于MEO SAR大场景中的多普勒调频率分布，通过非正交非线性坐标系变换将两维空变集中在一维。在推导出的非正交非线性坐标系中，新的方位向对应于多普勒调频率等高线，因此，在该方向上的多普勒调频率空变可以最小化，在获得方位平移不变性的同时避免复杂的方位空变校正处理。然后，直接应用经典星载SAR成像算法来完成信号聚焦。为了实现更精确的方位压缩，采用多普勒重采样以抵消高阶多普勒参数的空变影响，并且消除由非线性坐标系变换引起的方位聚焦偏移。

2 信号建模

如图1描述了MEO SAR成像几何。S表示卫星位置，T表示照射区域的目标，β表示仰角，θa表示斜视角，θ表示入射角，在数据录取期间，轨道弯曲明显，MEO卫星与场景中目标的相对斜距历程很复杂。在本文中，相对斜距历程使用4阶泰勒展开模型表示，将斜距在多普勒中心时刻扩展为

其中，ST是从卫星S到目标T的向量，R0表示波束中心时刻雷达到目标的中心斜距，ta表示方位慢时间，tc表示目标波束中心时刻，qi,i1,2,3,4表示第i项的多普勒系数。多普勒中心与线性分量直接相关，多普勒中心表示为：fdc−2q1/λ,λ是电磁波波长。多普勒调频率可以用二次项系数表示为fdr−4q2/λ，为了实现方位向聚焦，需要准确计算二次项。

用将距离模型的2阶系数展开为方位时间与距离的函数

类似地，3阶系数可以展开为

其中，rR0−Rref是与场景中心相关的距离偏移，Rref是场景中心斜距，qij,xy是qi关于x和y的第j阶泰勒展开式系数，高阶量一般忽略不计。

图1 MEO SAR成像几何示意图Fig.1 MEO SAR imaging geometry

3 最优成像坐标系聚焦算法

3.1 最优成像坐标系

图2给出了场景中不同目标多普勒调频率在不同成像坐标系中的分布情况，黑色曲线组表示等多普勒调频率线。图2(a)表示原始回波录取坐标系，横轴表示方位时间，纵轴表示距离，在该坐标系中由于卫星速度随时间变化以及轨道的弯曲，多普勒调频率存在沿方位向的非线性变化[21]。本文通过调整场景中的多普勒调频率分布来解决方位空变的问题。图2(b)为非正交坐标系中将数据进行斜置后的多普勒调频率分布，对不同方位时间的脉冲信号进行了线性距离平移操作，此时多普勒调频率方位的方位线性变化量得到了消除，只剩余了二次变化。在图2(c)所示的非线性非正交坐标系，经过对不同时刻的信号进行了非线性的平移，可以使等多普勒调频率线沿水平向分布，信号在方位向上满足平移不变性。从图2(a)到图2(b)和图2(c)的成像坐标系变化能够利用类似距离徙动校正的距离偏移函数来实现，而不同方位时刻的距离徙动量根据多普勒调频率的分布得到。

为了最小化多普勒调频率方位向上的线性与非线性变化，距离移动量包含线性项与二次项

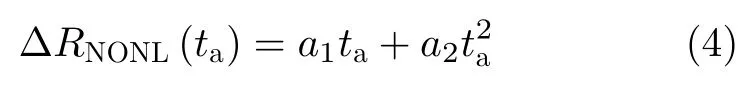
则最优成像坐标系变换函数可以表示为

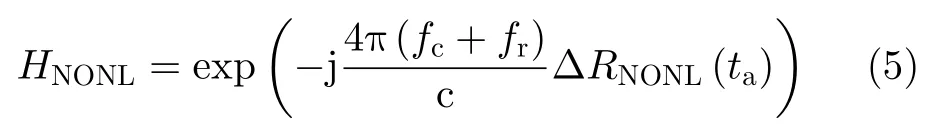
其中，定义fc为载频，c为电磁波的传播速度，fr为距离向频率。参数a1与a2需要根据多普勒调频率的空变特性求解。

在最优成像坐标系变换之后，斜距历程为

在最优成像坐标系变换之后，多普勒如

其中O(ta)为ta的高阶项。令fdcfdc(0)，得到新的方位聚焦时间，ta的高阶项影响较小可以忽略，那么有

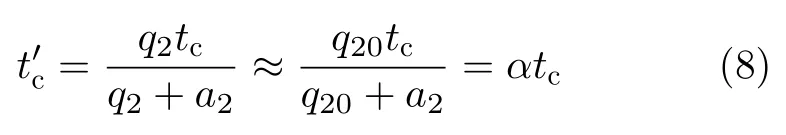
其中，用αq20/(q20+a2)表示方位时域尺度变化因子。

方位时移会引起目标聚焦位置的变化，可近似表示为

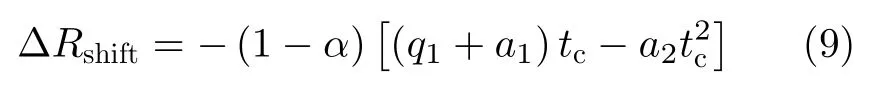
那么，新的斜距历程变为

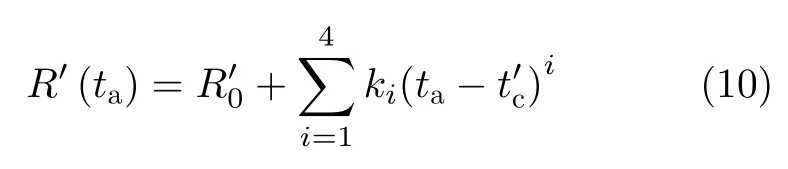
ki,i1,2,···,4是在新的方位聚焦时间t′c下新的距离系数。具体表达式为

为了使距离单元偏移(Range Cell Migration,RCM)的方位空变最小，在参考距离处进行最优成像坐标系变换后，假设在方位向2阶系数k2为常数，令为零，可以得到最优坐标系转换函数中的参数a1与a2

图2 多普勒调频率平面坐标系Fig.2 Doppler rate plane

3.2 聚焦算法

在上述最优成像坐标系转换的基础上，本文提出了一种新的MEO SAR聚焦算法，如图3所示。

该算法首先利用最优成像坐标系转换函数处理多普勒调频率空变的问题；接着，利用距离非线性频调变标算法(Nonlinear Chirp Scaling Algorithm,NCSA)[22]或距离徙动算法(Range Migration Algorithm,RMA)[23]补偿距离徙动；然后，用多普勒重采样补偿多普勒参数且校正最优成像坐标系转换造成的聚焦时移；最后利用几何形变校正来处理算法带来的聚焦位置偏移，从而获得最终的聚焦图像。

在最优成像坐标系变换步骤中，没有考虑高阶距离系数的变化。三次距离系数的方位空变可能会导致非中心目标的旁瓣不对称，二次距离系数中的交叉项可能会导致场景角落的目标聚焦深度下降。为了实现更精确的方位聚焦，在最优成像坐标系变换之后，数据变换到方位时域之前，需要校正高阶多普勒参数和距离-方位耦合的空变分量。文献[21]提出使用与距离相关的多普勒重采样实现精确的方位聚焦。本文提出使用基于文献[21]的改进多普勒重采样方法实现多普勒线性化与方位时移校正。此改进的多普勒重采样方法仅多普勒重采样函数与文献[21]不同，其余多普勒重采样步骤请参考文献[21]。

图3 聚焦算法流程图Fig.3 Flowchart of the proposed imaging algorithm

在多普勒域，方位匹配滤波器可以被表达为

其中，φ在式(16)中给出

根据式(14)中的剩余空变和式(8)中目标的方位偏移因子，构造一个改进的多普勒重采样函数

其中，p21(rnew)与p31是多普勒参数关于时间的导数，其表达式在式(18)中给出。

根据式(18)在多普勒域中对数据进行重采样，能够消除残余的多普勒调制项，并校正方位聚焦偏移。

成像坐标系变换引入的几何畸变，可以在方位压缩后通过在距离频域乘以线性校正函数式(19)来校正

完成几何校正后，即可获得良好的聚焦图像。

4 仿真分析

在本节中，将使用表1中的MEO SAR参数进行仿真实验，以验证所提出的方法。轨道高度为13000 km，在100 km的场景中布置了11 × 11个点目标(如图4所示)，能够实现2 m方位分辨率。为了评估本文所提方法对场景中不同点目标的聚焦效果，挑选3个典型的点目标A,B,C进行了分析，并且将本文方法与文献[21]中联合时间多普勒重采样算法(Joint Time-Doppler Resampling,JTDR)、常规的文献[22]中非线性频调变标算法(NCSA)进行对比分析。

图5给出了在坐标系变换前和变换后，目标斜距与多普勒调频率的关系。通过对坐标系变换前后的斜距系数进行拟合，可以对比多普勒调频率的变化情况。在坐标系变换之前，相同斜距但具有不同波束中心时间的目标的多普勒调频率分布在较宽的范围内。在坐标系变换之后，所有目标在多普勒调频率-距离平面内严格分布在一条线上，说明此时方位向上多普勒调频率是恒定的。

图6给出了文献[22]中NCSA算法得到的仿真结果，只有中心目标聚焦良好。

图7给出了文献[21]中JTDR算法得到的仿真结果，选定的3个目标都聚焦良好，方位峰值旁瓣比(Peak SideLobe Ratio,PSLR)低于–13.26 dB，方位积分旁瓣比(Integrated Sidelobe Ratio,ISLR)低于–10.14 dB(具体数值见表2)，因此，文献[21]中的算法对于MEO SAR聚焦是有效的。

图8给出了本文所提算法得到的仿真结果，选定的3个目标都聚焦良好，方位PSLR低于–13.25 dB，方位ISLR低于–10.06 dB(具体数值见表2)。

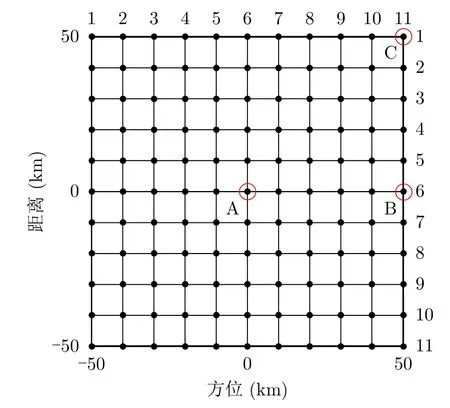
图4 仿真场景目标分布Fig.4 Arrangement of simulated targets

表1 仿真参数Tab.1 Simulation parameters

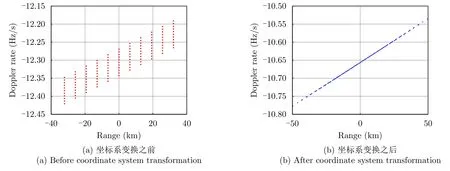
图5 目标斜距与多普勒调频率的关系Fig.5 Relationships between Doppler rates and ranges of the simulated targets

图6 文献[22]中NCS算法的点目标仿真结果Fig.6 Simulation results using the NCS algorithm in Ref.[22]

图7 文献[21]中的JTDR算法的点目标仿真结果Fig.7 Simulation results using the JTDR algorithm in Ref.[21]

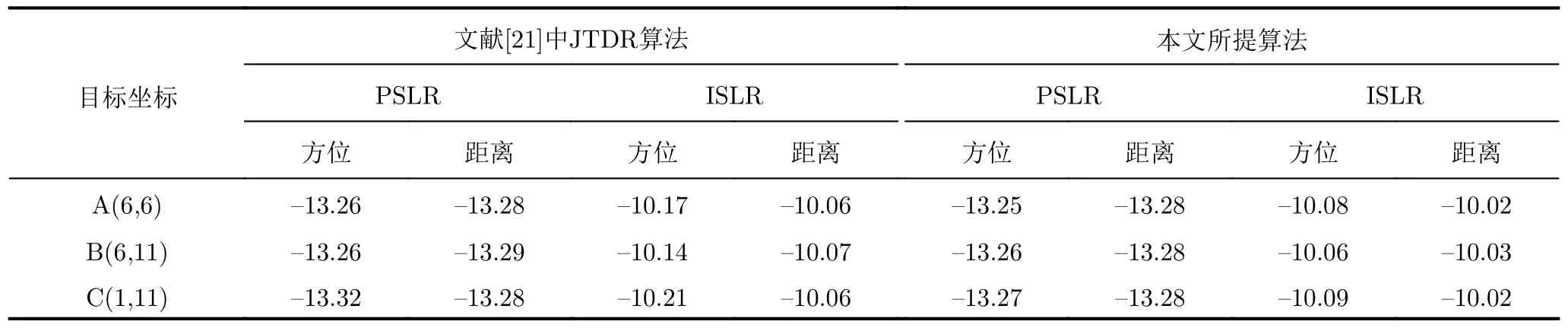
表2 文献[21]中JTDR算法与本文所提算法仿真PSLR及ISLR数值Tab.2 Compare of simulated values of PSLR and ISLR using the JTDR algorithm in Ref.[21] and the proposed method

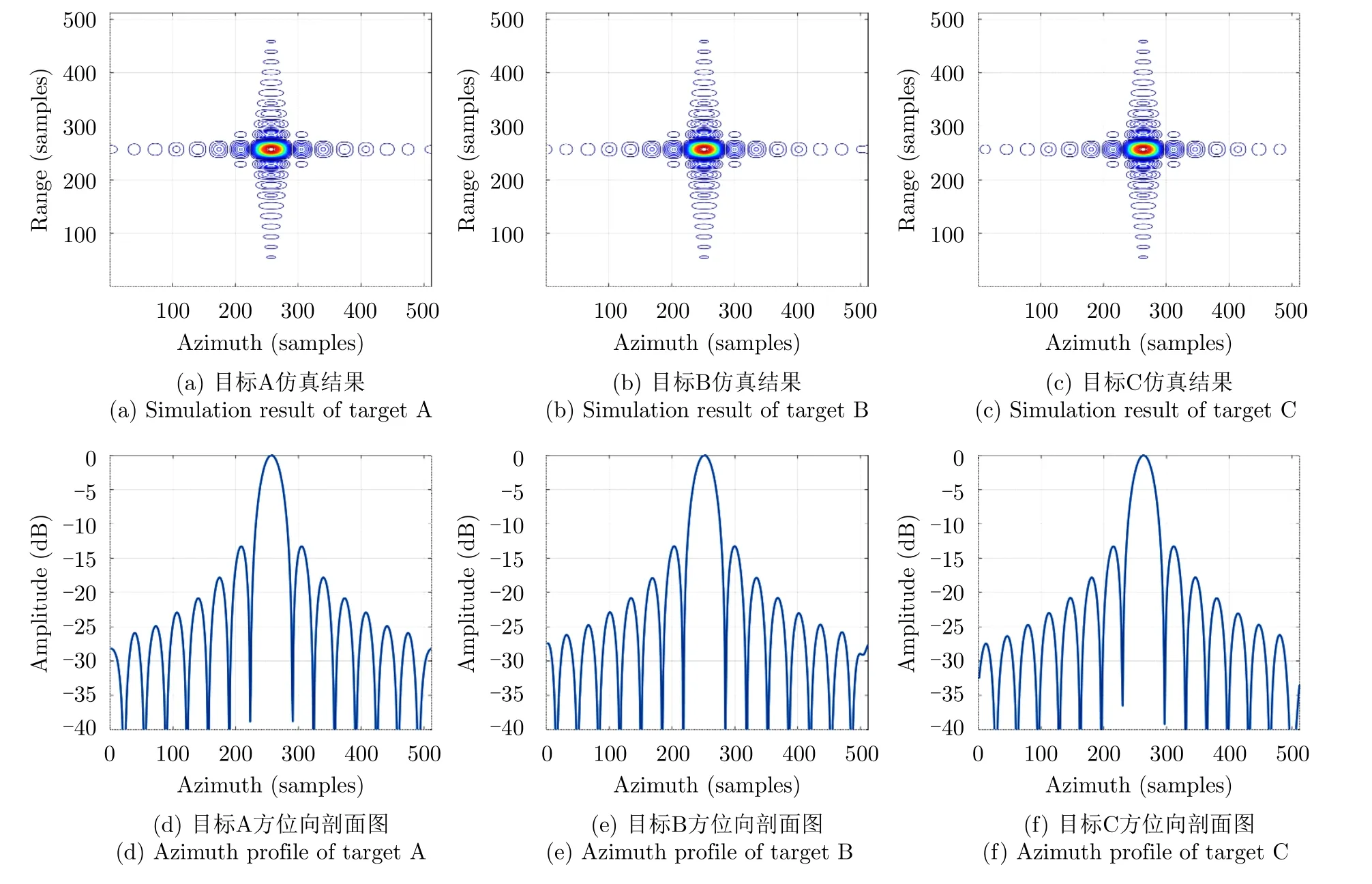
图8 本文所提算法的点目标仿真结果Fig.8 Simulation results using the proposed method

因此，本文所提算法对于MEO SAR聚焦是有效的，并且聚焦效果与文献[21]中的JTDR算法基本一致。

下面针对本文算法的计算复杂度进行仿真分析。假设信号距离向有M个采样点，方位向有N个采样点。用距离向的非线性频调变标(NCSA)实现距离单元徙动校正。所提方法包括4个距离向的FFT/IFFT，两个方位向的FFT/IFFT,4个相位乘法，1个方位向插值。sinc插值核的的长度是K。总的计算复杂度是

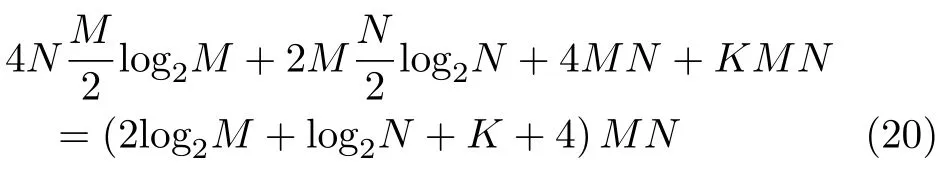
图9给出了3种算法运算量随场景大小的变化关系，可以看出本文算法的运算量介于改进的NCS算法和JTDR算法之间。这主要是多普勒重采样操作引入了较大的运算量，事实上如果适当放宽对场景角落点的聚焦深度要求，不进行重采样操作，那么本文算法的运算量将接近改进的NCS算法。

可见，本文所提算法实现良好聚焦效果的同时，运算量比参考算法低。

5 结论

本文提出一种基于最优成像坐标系变换的MEO SAR数据处理算法。相对于分别处理两维空变的常规处理算法，本文提出一种非正交非线性坐标系转换，在该坐标系中信号满足方位平移不变性，因此可以采用类似LEO SAR的处理算法进行MEO

图9 不同算法运算量对比Fig.9 Computation comparison using different methods

SAR的数据处理。与常规方法相比，由于简化方位空变的校正处理，因此能够显著降低算法的运算量。另外，针对波束扫描模式(如滑动聚束/TOPS模式等)，需要采用子孔径处理、或者两步法方位解模糊处理，本文提出的新的空变处理方法，经过改进后结合预处理，也能够应用于其他模式的数据处理中。