流固耦合对三螺杆泵的螺杆振动影响
2020-10-23朱博文赵永强
朱博文,赵永强,2*
(1.陕西理工大学 机械工程学院, 陕西 汉中 723000;2.陕西省工业自动化重点实验室, 陕西 汉中 723000)
三螺杆泵具有流量平稳、压力脉动小、自吸能力强、振动小、效率高等优点,常用于船舶、电力、机床、电梯等领域。三螺杆泵的核心部件是三根互相啮合的主、从动螺杆,主动螺杆转动带动两根从动螺杆高速运转,从而实现吸、排的工作流程。三螺杆泵适合于高压、高速、大流量的工况,而泵的连续可靠运行尤为重要。因此,需要对三螺杆泵的主、从动螺杆的工作特性进行分析研究。
国内外学者在三螺杆泵的力学性能、流场仿真和振动等方面开展研究工作,如袁玮玮等[1]利用流固耦合方法对螺杆膨胀机转子的力变形进行分析,采用有限元模拟内部流场,将计算出气体压力耦合到转子表面,计算出转子的变形量;刁安娜等[2]利用CFD技术,分析了螺杆压缩机排气腔内的压力、温度、速度的分布和涡带的变化,得到了不同工况下排气压力脉动的分布;Stosic N等[3]对喷油螺杆压缩机在冷却过程中转子的结构采用CFD技术进行了仿真;Selvaraji M等[4]利用CFD技术对非接触迷宫密封式转子型线的螺杆压缩机进行了仿真;刘厚林等[5]通过对叶轮出口处的压力和相对速度分布,分析了流固耦合对外特性预测值影响的内流机理;肖若富等[6]对水轮机固定导叶在水中的固有频率和固有振型进行解析,对固定导叶在运行过程中产生的共振进行了分析预测;权凌霄等[7]对斜轴式轴向柱塞泵壳体结构进行振动谐响应分析;赵慧[8]利用有限元软件建立了螺杆压缩机转子的网格模型和模态分析;李瑞超等[9]对3D打印喷头利用有限元软件进行了流固耦合分析和结构优化;吴慧媛等[10]对双螺杆压缩机进行了流场动力学特性分析;吴高捷等[11]通过ANSYS对双螺杆膨胀机的转子进行了模态分析;张智伟等[12]对LNG低温潜液泵转子部件进行了流固耦合下模态分析;齐立龙[13]对双向泵叶片进行了流固耦合的应力和模态分析;陈宇杰等[14]研究了轴流泵转子系统在水中的模态以及水介质对于模态的影响,分析了共振规律。
上述研究的对象为双螺杆压缩机、双螺杆泵和柱塞泵等,未涉及三螺杆泵;所采用的数值分析方法为本文对三螺杆泵的模态分析提供了参考。由于三螺杆泵的特殊结构和封闭密封腔的特性,使得其内部振动的模拟变得复杂。本文采用流固耦合方法,对三螺杆泵在无预应力状态下和流固耦合作用下的模态分别进行计算,并对计算结果进行比较,研究三螺杆泵在工作情况下的振动变化规律及其对工作特性的影响。
1 模态分析计算
对三螺杆泵的研究集中在泵工作过程中螺杆的应力变形情况,固有频率由结构本身的属性决定,在对三螺杆泵的螺杆进行模态分析时,需要对结构进行简化。依据达朗贝尔理论得到三螺杆泵中的主、从动螺杆的动力学方程为[11]
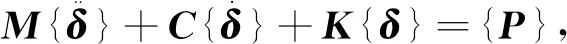
(1)
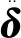
在自由模态分析时忽略外载荷的作用和阻尼,则简化后的方程为
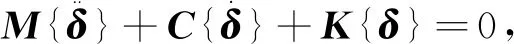
(2)
由式(2)得:
{δ}={φ}sin(ω(t-t0)),
(3)
式中φ为n阶特征向量,ω为向量φ的振动频率,t为时间变量,t0为初始条件时间常数。
由式(2)和式(3)可得:
(K-ω2M){φ}=0,
(4)
式(4)有非零解的充要条件是
|K-ω2M|=0,
(5)
当M和K的阶数为n,ω2为特征值,可求得第i阶振动频率ωi,进一步可求得第i阶模态的特征向量。
2 有限元模型
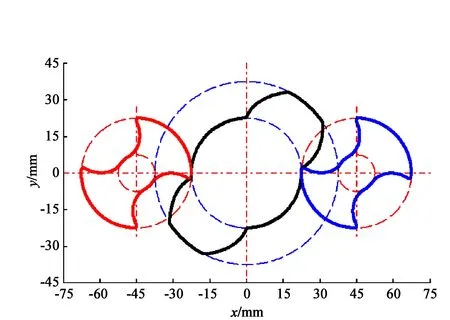
图1 螺杆的端面型线
在现有三螺杆泵端面型线的基础上,采用圆弧修正方法对从动螺杆的尖点进行圆弧过渡。使从动螺杆的接触点内移,以减小主、从动螺杆之间的磨损。图1为MATLAB软件中建立的主、从动螺杆的数学模型和端面啮合型线。
根据表1的螺杆参数,在三维软件UG中导入螺杆的端面型线,建立主、从动螺杆的三维实体模型如图2所示。将主、从动螺杆的模型进行网格划分,主、从动螺杆采用四面体网格划分,在螺杆的螺杆表面进行加密划分,最终得到的网格模型如图3所示。

表1 主、从螺杆的基本参数
本文采用有限元分析软件ANSYS对主、从动螺杆进行模态分析,螺杆的材料选取屈服强度和耐磨性较高的38CrMoAl,其力学参数如表2所示。
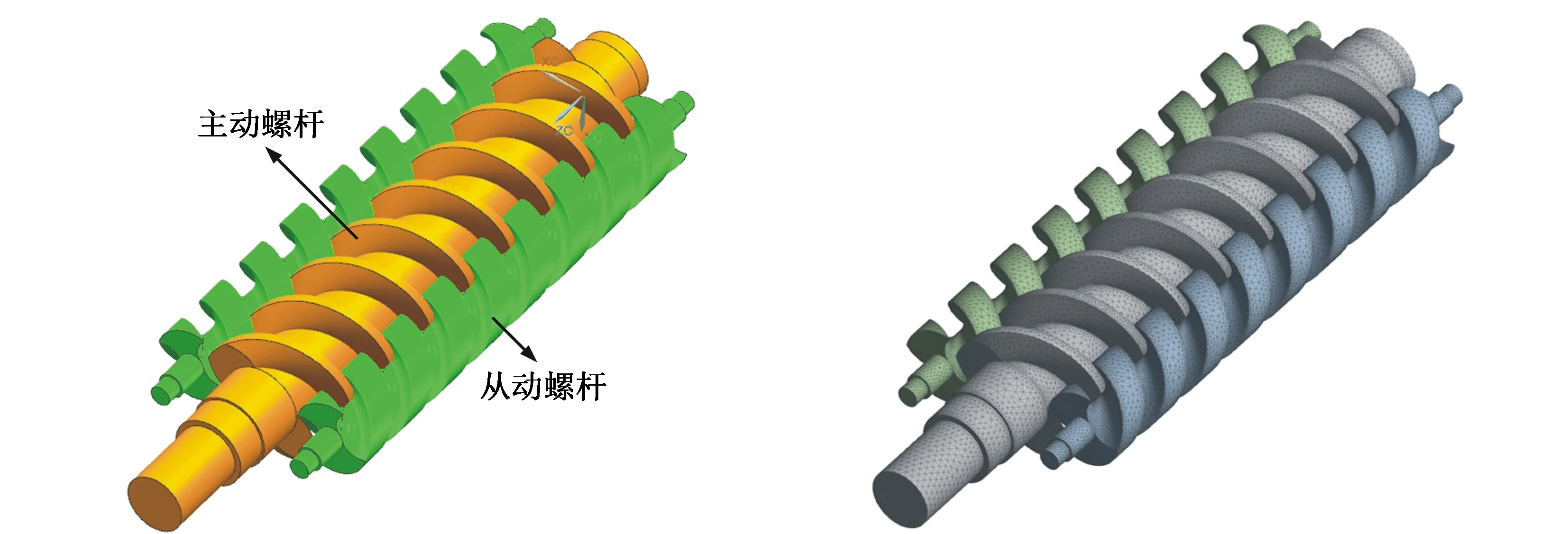
图2 主、从动螺杆模型 图3 主、从动螺杆网格模型

表2 38CrMoAl材料参数
3 螺杆的模态分析
3.1 螺杆在自由状态的模态分析
对划分好网格的螺杆模型设置边界条件,只保留螺杆沿轴向转动的自由度,限制其余自由度后,仿真三根螺杆的前6阶的模态如图4所示。
从图4的模态分析云图中可以看出:一阶与三阶的振型主要表现在主、从动螺杆的中间部位发生上下弯曲振动,且最大变形位置都发生在螺杆的齿面上,这是由于变形部位远离轴端,扰度较大,变形量较大;二阶振型在从动螺杆发生左右振动,且最大变形位置发生在从动螺杆的外侧,而主动螺杆变形较小;四阶振型呈波浪状振动,且最大变形位置发生在靠近轴端的从动螺杆齿面上;五阶振型沿着轴向的伸缩振动,最大变形位置在轴端处;六阶振型呈弯曲振动,在主、从动螺杆中部变形最小,从动螺杆在靠近轴端外侧变形最大。
表3列举了螺杆的前6阶模态的频率f和振幅A,从表中可以发现:随着模态阶数的增加,螺杆的频率变大,且二阶和三阶的频率相近,四阶与五阶频率相近,一阶、三阶和五阶的振幅相近。

表3 螺杆的自由模态分析结果
3.2 螺杆在流固耦合作用下的模态分析
通过CFD方法对三螺杆泵内部流场进行仿真分析,边界条件为:内部流动介质采用46号液压油,流体的计算温度323 K。在323 K时流体的参数为:密度ρ=890 kg/m3,动力粘度μ=0.046 Pa·s,热导率为0.12 W/(m·K),比热容为1890 J/(kg·K)。三螺杆泵的入口设置为0.1 MPa的压力入口,出口设置为10 MPa的压力出口;将主、从动螺杆的外壁设为静止壁面,一根主动螺杆表面和两根从动螺杆的表面设为转动壁面。主、从动螺杆以相同的角速度ω1、ω2反向旋转,带动物料在泵内部做螺旋运动。
通过ANSYS Workbench中的Static Structural模块,将上述三螺杆泵内流场计算的压力作为外载荷导入到主、从动螺杆的表面。三螺杆泵的主、从动螺杆的支承方式采用一端固定,另一端游支。主动螺杆与电机输出轴相连输入动力,主动螺杆绕着Z轴转动,两根从动螺杆均由主动螺杆带动转动。因此主、从动螺杆与各自轴承的连接处设置径向和轴向约束,将泵内的流体压力载荷分别加载在主、从动螺杆的螺旋槽内,其效果如图5所示。如图6所示在流固耦合作用下的最大变形量为0.068 6 mm,最大变形发生在从动螺杆的两侧[15]。
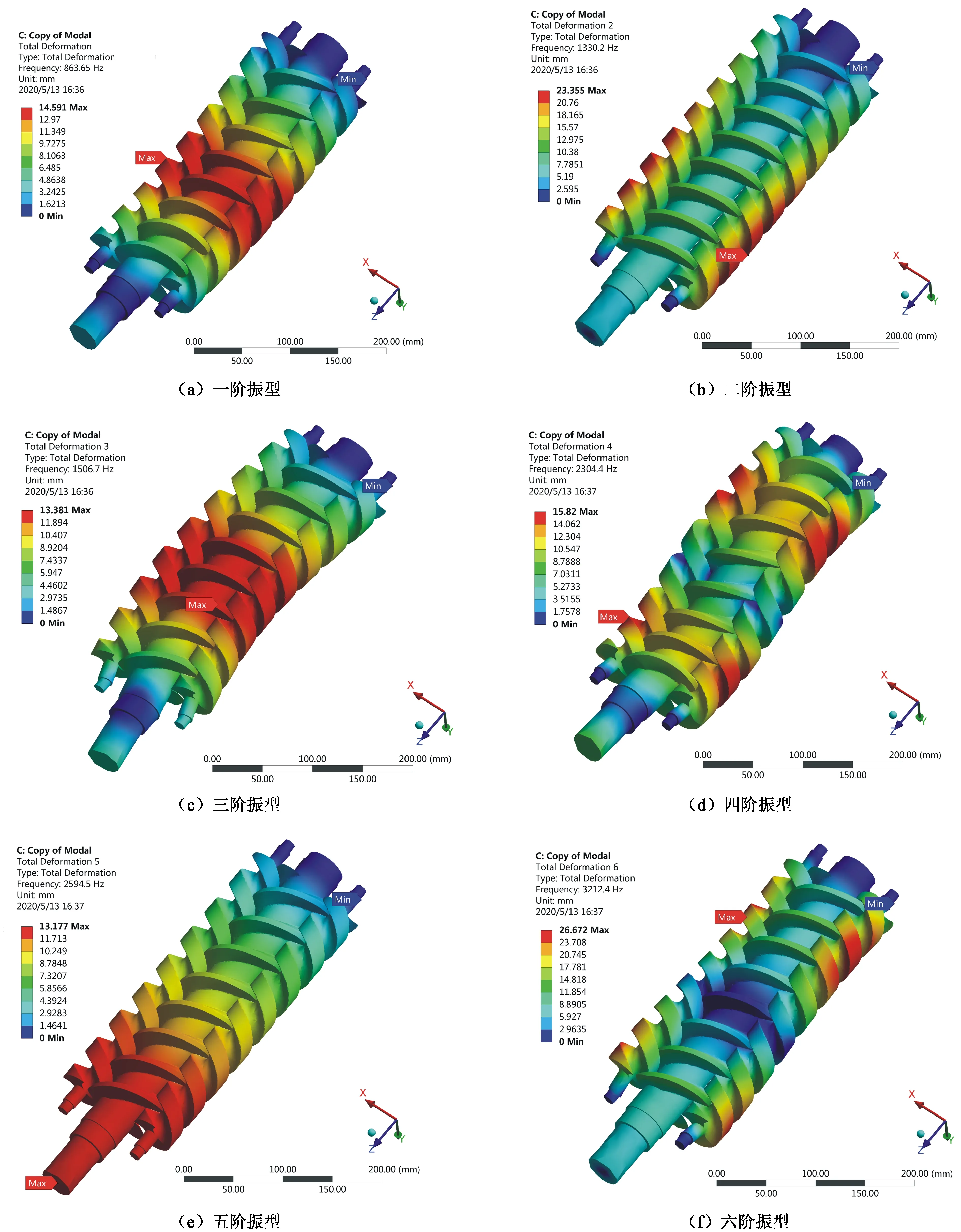
图4 无预应力下螺杆前6阶的模态振型图
10 MPa的出口压力依次增加0.1、0.3、0.5 MPa后,与不同螺杆转速进行组合,在流固耦合条件下,仿真得到主、从动螺杆的最大变形量关系如图7和图8所示。
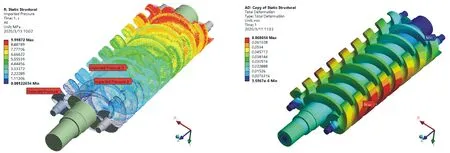
图5 螺杆流体压力加载 图6 流固耦合作用
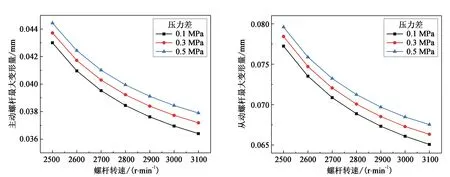
图7 不同转速对主动螺杆变形影响 图8 不同转速对从动螺杆变形影响
从图7可以看出,螺杆转速一定时,主动螺杆的最大变形量随着泵的出口压力的增大而增大;主动螺杆转速为2500 r/min时,泵的出口压力每增大0.1 MPa,则变形量增加0.003 5 mm;而主动螺杆转速为3100 r/min时,泵的出口压力每增大0.1 MPa,则变形量增加0.003 9 mm。主动螺杆的最大变形量随着转速的增加而减小,当泵的出口压力为10.1 MPa时,转速每增加100 r/min,变形量减少约0.012 mm;当泵的出口压力为10.5 MPa时,主动螺杆的转速每增加100 r/min,其变形量减少约0.009 mm。
从图8可以看出,螺杆转速一定时,从动螺杆的最大变形量随着泵的出口压力的增大而增大;从动螺杆转速为2500 r/min时,泵的出口压力每增大0.1 MPa,则变形量增加0.005 8 mm;而从动螺杆转速为3100 r/min时,泵的出口压力每增大0.1 MPa,则变形量增加0.006 1 mm。从动螺杆的最大变形量随着转速的增加而减小,当泵的出口压力为10.1 MPa时,转速增加100 r/min,变形量减少约0.018 5 mm;当泵的出口压力为10.5 MPa时,从动螺杆的转速每增加100 r/min,其变形量减少约0.001 86 mm。
将主、从动螺杆的流固耦合计算结果作为预应力,并导入模态分析,得到主、从动螺杆的流固耦合作用下的模态分析结果如图9所示。
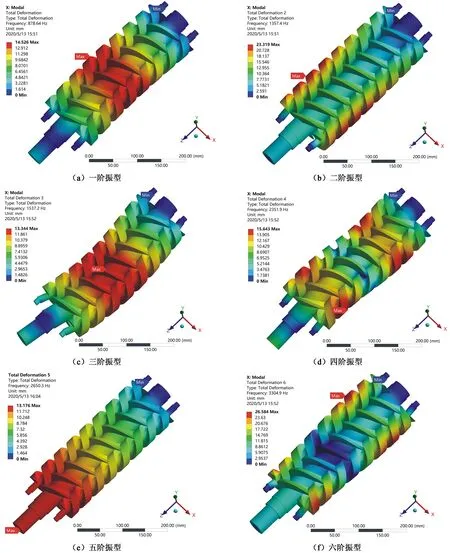
图9 流固耦合作用下螺杆前6阶的模态振型图
从图9中可以看出:添加了流固耦合作用力后,各阶模态的摆动幅度和变化趋势没有明显的改变,只是频率和振幅发生了变化。频率发生变化的原因是由于流体压力导致螺杆发生变形,使整个结构发生了变化,因此频率比原有频率略为增加。
表4为两种不同工况下的主、从动螺杆模态分析结果对比。从表中可以发现:随着模态阶数的增加,螺杆的频率也会随之变大,且二阶和三阶的频率相近,四阶与五阶频率相近。一阶、三阶和五阶的振幅都基本接近。添加流固耦合预应力后,主、从动螺杆各阶振幅都有所减小,导致产生这一现象的原因是,流体压力对螺杆产生的变形与振动产生的变形方向并不相同,抵消了部分变形作用。

表4 无预应力作用下和流固耦合作用下螺杆的模态分析
将表4中的数据绘制成折线如图10所示,而流固耦合作用下螺杆的振幅曲线如图11所示。在图10中,无预应力和流固耦合状态下的频率变化规律基本相同,主、从动螺杆各阶的固有频率都呈小幅递增关系,且第五阶和第六阶的固有频率变化较大,在此阶振型的流固耦合状态下频率增大了2.8%。
而图11中,相同工作条件下,从动螺杆的第三阶振型和第五阶振型的振幅比主动螺杆小,而其他阶的振幅比主动螺杆大,其原因在于:此振型下主、从动螺杆都绕轴线转动发生不明显的变形,由于啮合间隙使得主动螺杆与从动螺杆之间产生碰撞,另外结构的差异也使得主动螺杆的齿间容积较大,这两种因素均造成主动螺杆的振幅要大于从动螺杆的振幅。
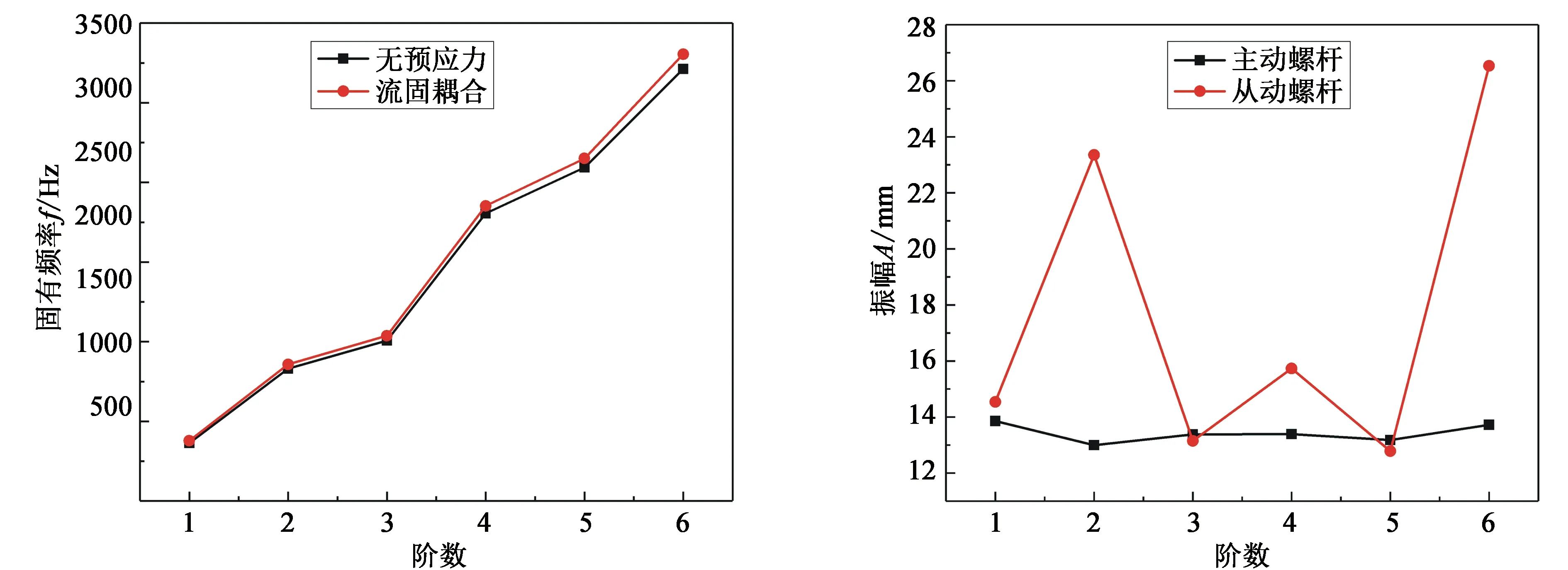
图10 流固耦合作用下和无预应力下螺杆频率变化 图11 流固耦合作用下螺杆振幅变化
3.3 激励频率的计算
三螺杆泵在实际工作中,电动机驱动主动螺杆,主动螺杆带动两根从动螺杆工作。主、从动螺杆的转速与激励频率fn之间的关系为
(6)
通过式(6)计算,当转速为2900 r/min,得到螺杆的激励频率为48.3 Hz,远小于一阶固有频率,螺杆在工作中不会发生共振。
4 结论
本文通过对螺杆进行有限元分析,利用ANSYS中流场、应力场和模态相结合进行数值模拟,得到了三螺杆泵的主、从动螺杆在流固耦合条件下的模态分布规律,并与自由条件的模态仿真结果进行对比,结果显示:
(1)在自由条件下随着模态阶数的增加,主、从动螺杆的固有频率随之变大,且二阶和三阶的频率相近,四阶与五阶频率相近。
(2)通过分析三螺杆泵的主、从动螺杆在流固耦合状态下的变形情况,发现主、从动螺杆的最大变形量随着流体压力的增大而增大,当螺杆转速为2500 r/min时,泵的出口压力每增大0.1 MPa,主、从动螺杆变形量分别增加0.003 5 mm和0.005 8 mm;在螺杆转速为3100 r/min时,泵的出口压力每增大0.1 MPa,主、从动螺杆变形量分别增加0.003 9 mm和0.006 1 mm。主、从动螺杆的最大变形量随着螺杆转速的增加而减小,当泵的出口压力为10.1 MPa时,螺杆转速每增加100 r/min,主、从动螺杆的变形量分别减少约0.012 mm和0.018 5 mm;当泵的出口压力为10.5 MPa时,螺杆转速每增加100 r/min,主、从动螺杆的变形量分别减少约0.009 mm和0.001 86 mm。
(3)添加流固耦合预应力后,主、从动螺杆的各阶振型变化趋势基本一致,也随着模态阶数的增加,固有频率随之增大。频率发生变化的原因是由于流体压力导致螺杆发生变形,使整个结构发生了变化,因此频率比原有频率略有增加。各阶振幅都有所减小,导致产生这一现象的原因是,流体压力对螺杆产生的变形与振动产生的变形方向并不相同,抵消了部分变形作用。
通过模态分析,可以为螺杆部件的结构设计和优化提供参考,避免因共振而影响机器的正常运转,同时为三螺杆泵的动态特性奠定基础。
