神经网络方法求解绝对值方程及线性互补
2020-10-23雍龙泉
雍龙泉
(1.陕西理工大学 数学与计算机科学学院, 陕西 汉中 723000;2.陕西省工业自动化重点实验室, 陕西 汉中 723000)
绝对值方程(Absolute Value Equations,AVE)是指:
Ax-|x|=b,
(1)
其中A∈Rn×n,x、b∈Rn,|x|表示对x的各个分量取绝对值。绝对值方程的研究来源于两个方面,一个是区间线性方程,另一个是线性互补问题。由于任意的线性互补都能转化为绝对值方程,而绝对值方程具有简单的结构,因此关于绝对值方程的研究引起了众多学者的关注[1-2]。其中Rohn[3]在理论方面做出了奠基性的工作,Mangasarian[4-7]在理论和算法方面做出了巨大的贡献,指出绝对值方程等价于双线性规划,并给出了相应的求解算法。
近年来,针对唯一解的绝对值方程,求解算法主要有5类:(1)通过把绝对值方程转化为线性互补问题进行求解[1];(2)把绝对值方程转化为一个非光滑方程,采用广义牛顿法或非光滑牛顿法进行求解[7-10];(3)通过光滑处理,绝对值方程转化为一个光滑优化问题,采用光滑牛顿法求解[11-18];(4)采用矩阵分裂技术,求解某些具有特殊结构的绝对值方程[19-24];(5)采用神经网络方法进行求解[25-30]。此外,智能优化算法近年来也用于求解绝对值方程[31]。针对多个解的绝对值方程,可以借助聚类技术,找到尽可能多的解,该方面研究较多的是具有2n个解的绝对值方程[32-34]。此外,针对多个解的绝对值方程,稀疏解的研究目前也成为了一个热点[35-37]。
本文选取逼近性质较好且不易发生溢出的一致光滑逼近函数来处理绝对值方程,建立求解无约束优化问题的梯度下降神经网络模型,并应用于求解绝对值方程和线性互补问题。
文中I表示单位矩阵,‖‖表示2范数。
1 绝对值函数的一致光滑逼近函数
定义1(光滑逼近函数) 给定非光滑函数f(t):R→R,我们称光滑函数fμ(t),μ>0为f(t)的光滑逼近函数,如果∀t∈R,存在κ>0,使得
|fμ(t)-f(t)|≤κμ,∀μ>0,
如果κ不依赖于t,则称fμ(t)为f(t)的一致光滑逼近函数[18,38-40]。
一致光滑逼近函数可以分为从上方一致逼近和从下方一致逼近。文献[38-39]给出了绝对值函数φ(t)=|t|的多个一致光滑逼近函数,为了便于研究,本文选取如下3个光滑函数:
下面给出这3个一致光滑逼近函数的性质[38-39]。

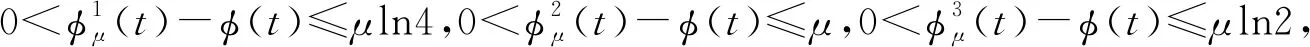

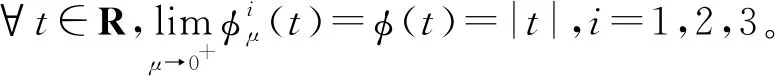

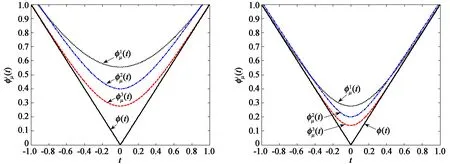
(a) μ=0.4 (b) μ=0.2图与φ(t)=|t|的图像
2 绝对值方程的光滑逼近处理
引理1[1]若A∈Rn×n,且矩阵A的所有奇异值都大于1,则矩阵A可逆,且‖A-1‖<1。
引理2[1](ⅰ)若A∈Rn×n,且矩阵A的所有奇异值都大于1,则∀b∈Rn,AVE存在唯一解;
(ⅱ)若A∈Rn×n,且矩阵A满足‖A-1‖<1,则∀b∈Rn,AVE存在唯一解。
引理3[16]若A∈Rn×n,且矩阵A满足‖A-1‖<1,矩阵D=diag(d1,d2,…,dn),这里|di|≤1,i=1,2,…,n,则A±D非奇异。
问题(1)等价于非线性方程组
H(x)=0,
(2)
其中H(x):=Ax-|x|-b。由于H:Rn→Rn是非光滑函数,以下构造一个光滑函数Hμ(x)来逼近非光滑函数H(x)。
定义2[17]给定非光滑函数H:Rn→Rn,称光滑函数Hμ:Rn→Rn(μ>0)为H的光滑逼近函数,如果∀x∈Rn,存在κ>0,使得
‖Hμ(x)-H(x)‖≤κμ,∀μ>0,
如果κ不依赖于x,则称Hμ为H的一致光滑逼近函数。
记向量绝对值函数φ(x)=|x|=(|x1|,|x2|,…,|xn|)T的每一个分量为
φ(xi):=|xi|,i=1,2,…,n,
对每一个φ(xi),采用定理1中的光滑函数
进行光滑化处理,就得到向量绝对值函数φ(x)的光滑逼近函数为
φμ(x)=(φμ(x1),φμ(x2),…,φμ(xn))T,
且每一个分量φμ(xi)满足
0<φμ(xi)-φ(xi)<μ,i=1,2,…,n。
从而有
于是当μ→0时,φμ(x)一致光滑逼近绝对值函数φ(x)。
通过上面的光滑处理,问题(2)转化为如下光滑方程组:
Hμ(x)=0,
(3)
其中Hμ(x)=Ax-φμ(x)-b,φμ(x)=(φμ(x1),φμ(x2),…,φμ(xn))T。
下面研究光滑函数Hμ(x)的一些性质。
定理2 ∀μ>0,Hμ(x)一致光滑逼近H(x)。
证明∀μ>0,由于Hμ(x)可微,且满足
则Hμ(x)一致光滑逼近H(x)。


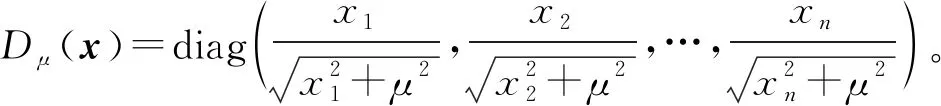

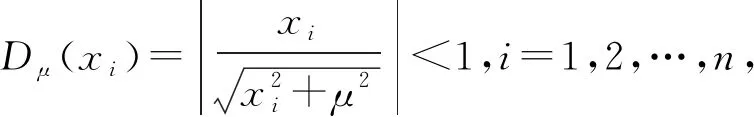
3 梯度下降神经网络模型
定义函数
(4)
称Eμ(x)为能量函数。到此,求解绝对值方程的近似解已经转化为求解连续可微的优化问题minEμ(x)。
定理4 ∀μ>0,矩阵A满足‖A-1‖<1,若Eμ(x)=0,则Eμ(x)=0。
证明∀μ>0,由于
Eμ(x)=[(x)]THμ(x),
梯度神经网络是基于求解问题(4)的最速下降模型的连续化形式,近年来已广泛应用于求解非线性互补、二阶锥规划等问题[41-45]。
下面给出求解光滑优化问题(4)的梯度下降神经网络模型:

(5)
这里参数τ表示梯度下降算法的步长。本文直接给出该神经网络的收敛性结果,详细的证明见文献[25-27]。
定理5 ∀μ>0,矩阵A满足‖A-1‖<1,神经网络(5)的平衡点是绝对值方程的解,反之,绝对值方程的解是神经网络(5)的平衡点。
下面采用模型(5)来计算一些常见的绝对值方程,以验证算法的有效性。
4 数值实验
给出3个绝对值方程(前2个具有唯一解,最后一个有4个解),通过将其转化为神经网络模型(5),采用四阶Runge-Kutta法求解微分方程组(对应MATLAB中的函数ode45),程序采用MATLAB R2009a编写。设置μ=0.01,终止条件Eμ(x)≤1.0×10-10。

算例4.1 考虑绝对值方程(1),其中
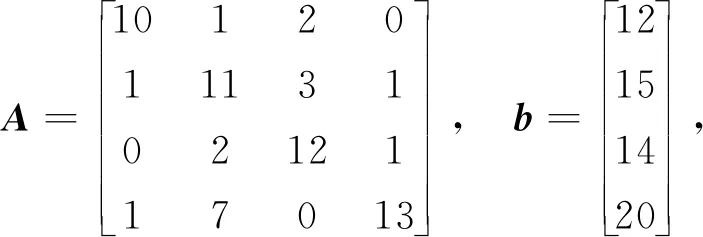
由于矩阵A的奇异值(SVD(A)=[17.434 9,12.262 9,9.638 9,7.598 4])大于1,因此该AVE问题存在唯一解x*=(1,1,1,1)T。表1给出了参数τ取不同值的计算结果;图2和图3分别给出了τ=100时近似解随时间的变化(轨线)及能量函数随时间的变化曲线。
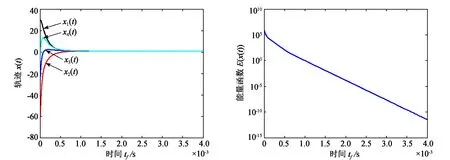
图2 近似解随时间的变化曲线 图3 能量函数随时间的变化曲线
算例4.2 绝对值方程(1)中所有奇异值大于1,矩阵A由如下MATLAB命令产生
rand(′state′,0);
R=rand(n,n);
A=R′*R+n*eye(n);
b=(A-eye(n,n))*ones(n,1)。
说明:给出矩阵维数n后,可以用上述代码产生和本文相同的数据,该AVE具有唯一解x*=(1,1,…,1)T。取不同的维数n,表1给出了参数τ取不同值的计算结果。图4给出了τ=100时维数n取10和50的能量函数随时间的变化曲线。

(a) 10维 (b) 50维图4 能量函数随时间的变化曲线
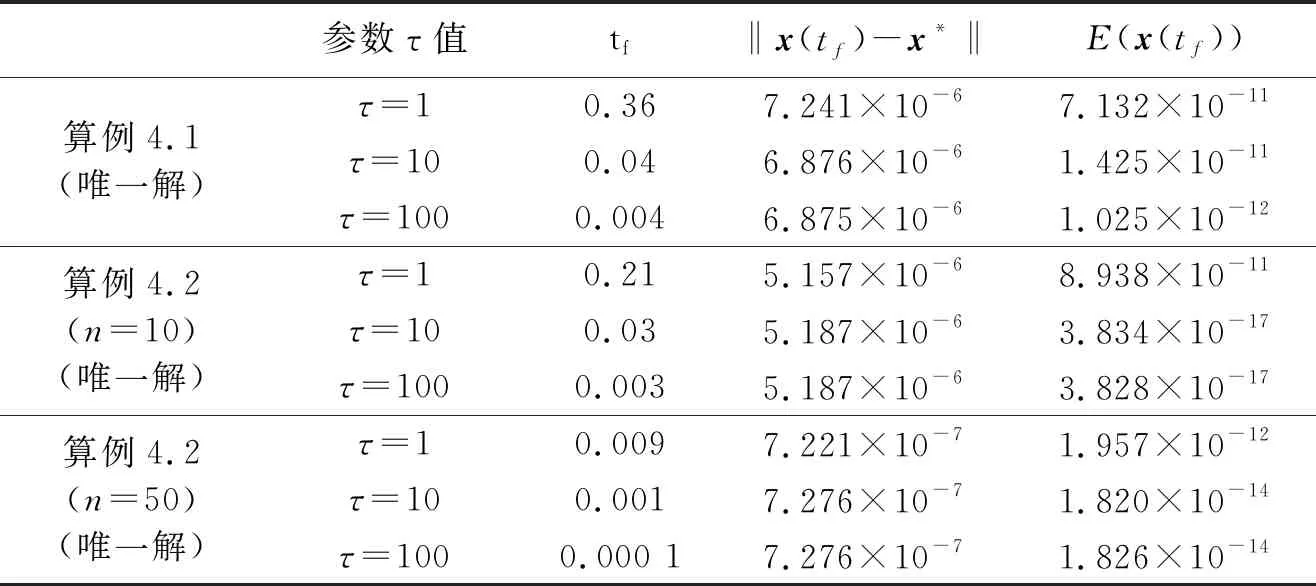
参数τ值tf‖x(tf)-x*‖E(x(tf))算例4.1(唯一解)τ=10.367.241×10-67.132×10-11τ=100.046.876×10-61.425×10-11τ=1000.0046.875×10-61.025×10-12算例4.2(n=10)(唯一解)τ=10.215.157×10-68.938×10-11τ=100.035.187×10-63.834×10-17τ=1000.0035.187×10-63.828×10-17算例4.2(n=50)(唯一解)τ=10.0097.221×10-71.957×10-12τ=100.0017.276×10-71.820×10-14τ=1000.000 17.276×10-71.826×10-14
算例4.3 考虑绝对值方程(1),其中


简单计算可得
图5给出了τ=100时,初始点在不同象限时的近似解随时间的变化曲线。
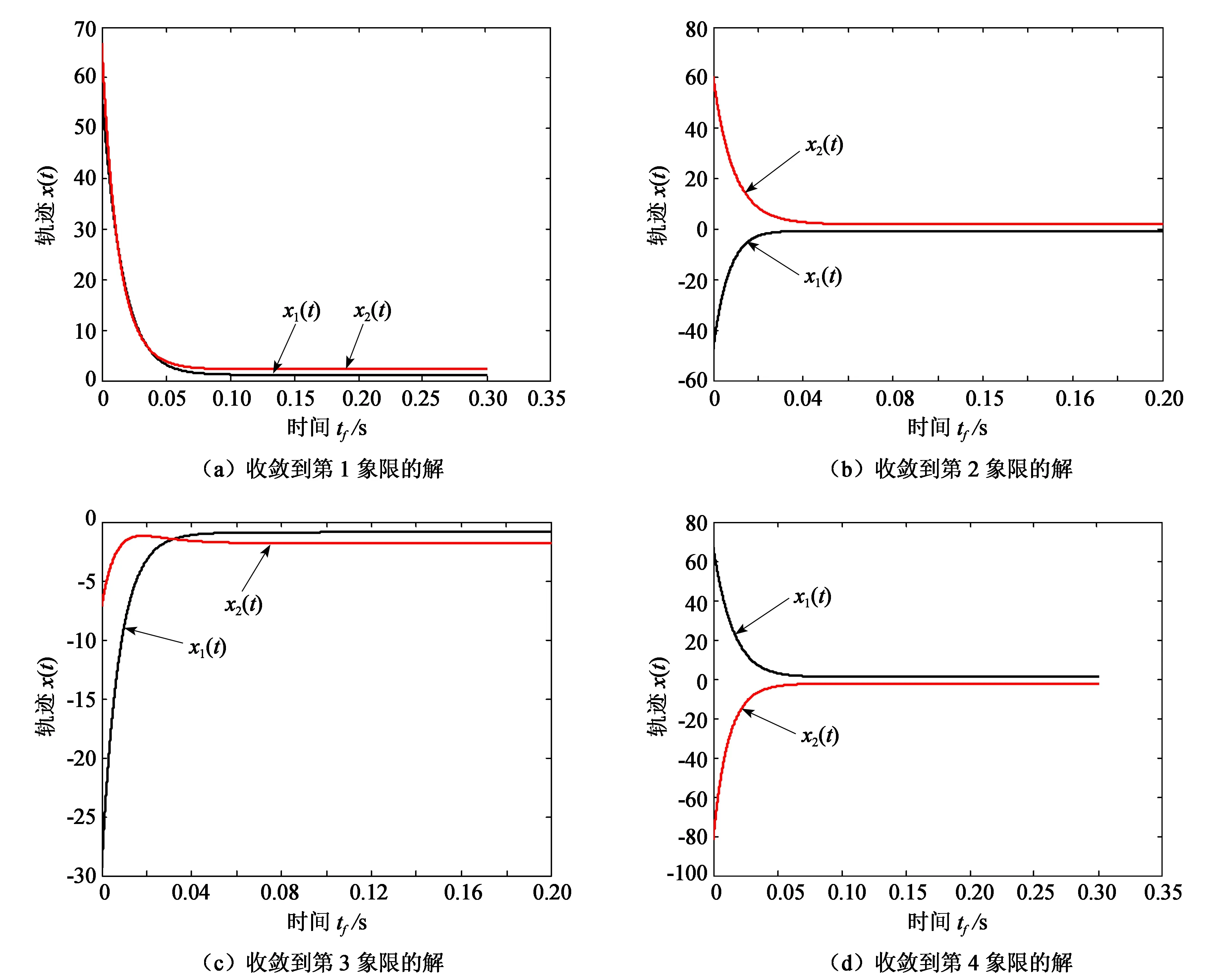
图5 初始点在不同象限时的收敛曲线
从图5可以看出,由于该问题的解分布在4个象限,初始点在哪个象限,则算法收敛到相应象限的解。
5 应用于线性互补问题
线性互补问题就是求一个向量z∈Rn,使得zT(Mz+q)=0,z≥0,Mz+q≥0。这里M∈Rn×n,q∈Rn,线性互补问题简记为LCP(M,q)。文献[2]中详细研究了AVE与LCP(M,q)的转化,指出若1不是矩阵M的特征值,则LCP(M,q)等价于绝对值方程(M+I)(M-I)-1x-|x|=((M+I)(M-I)-1-I)q,这里x=(M-I)z+q。
下面把上述方法应用于求解线性互补问题,为了便于计算,取初始点x(0)=(0,0,…,0)T,设置μ=0.01,终止条件Eμ(x)≤1.0×10-10。
算例5.1 考虑线性互补问题LCP(M,q),其中

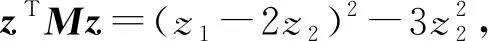
由于1不是矩阵M特征值,因此线性互补可以转化为绝对值方程Ax-|x|=b,这里A=(M+I)(M-I)-1,b=((M+I)(M-I)-1-I)q;简单计算可得
图6和图7给出了τ=100时,近似解随时间的变化(轨线)及能量函数随时间的变化曲线。

图6 近似解随时间的变化曲线 图7 能量函数随时间的变化曲线
算例5.2 考虑线性互补问题LCP(M,q),其中

∀z,这里z=(z1,z2,z3,z4)T。由于
这里z4前面的系数为0,因此矩阵M是半正定矩阵[46];且该线性互补问题具有唯一解z*=(2.5,0.5,0,2.5)T。由于1是矩阵M的特征值,因此令λ=3,则λM的特征值就不为1,且LCP(λM,λq)与LCP(M,q)具有共同最优解z*,而LCP(λM,λq)就可以转化为绝对值方程Ax-|x|=b,这里A=(M+I)(M-I)-1,b=((M+I)(M-I)-1-I)q;简单计算可得
图8和图9给出了τ=100时,近似解随时间的变化(轨线)及能量函数随时间的变化曲线。

图8 近似解随时间的变化曲线 图9 能量函数随时间的变化曲线
算例5.3 考虑线性互补问题LCP(M,q),其中

矩阵M是半正定矩阵[47],且该线性互补问题具有唯一解z*=(0,0,…,0,1)T。
取n=4,由于1是矩阵M的特征值,因此令λ=3,则λM的特征值就不为1,且LCP(λM,λq)与LCP(M,q)具有共同最优解z*,而LCP(λM,λq)就可以转化为绝对值方程Ax-|x|=b,这里A=(M+I)(M-I)-1,b=((M+I)(M-I)-1-I)q;简单计算可得
图10和图11给出了τ=100时,近似解随时间的变化(轨线)及能量函数随时间的变化曲线。

图10 近似解随时间的变化曲线 图11 能量函数随时间的变化曲线
6 结束语
本文选取逼近性质较好且不易发生溢出的光滑逼近函数来处理绝对值方程,通过构造梯度下降神经网络模型求解无约束优化问题而得到绝对值方程的近似解。结果表明该方法不依赖初始点,且具有收敛快等优点。文献[39]中系统地给出了绝对值函数的上方和下方一致光滑逼近函数,下一步可以通过改变光滑逼近函数,以期获得更好的计算结果。
