基于模糊信息公理与云模型的虚拟企业合作伙伴选择

2020-10-23赵金辉王学慧关文革尹立杰

运筹与管理 2020年1期

赵金辉，王学慧，关文革，尹立杰，周玉

(1.河北地质大学 a网络信息安全实验室，b宝石与材料工艺学院，河北石家庄 050031; 2.华北水利水电大学电力学院，河南郑州 450045)

0 引言

随着经济的发展与科技的进步，运作成本低、适应能力强、响应速度快的虚拟企业已经成为一种被广泛应用的企业经营模式[1]。虚拟合作伙伴的选择是构建虚拟企业的关键环节，恰当的合作伙伴直接关系到虚拟企业的绩效和成败[2,3]。目前，国内外学者对虚拟企业合作伙伴的选择作了一些研究，主要采用数学规划、多属性决策与模糊决策、精确算法和启发式算法四种理论方法[4]，通过设计与改进提出了多种模型和解决方案。文献[5]把虚拟合作伙伴选择划分为标准制定、量化和评价选择三个阶段，也是当前普遍采用的步骤。文献[6,7]采用数学规划方法，以响应时间、联接成本、合作风险为约束条件选择最好的合作伙伴。文献[8]针对信息不完整和不确定环境下的合作伙伴选择问题提出了基于扩展TOPSIS(Technique for Order Preference by Similarity to an Ideal Solution)法和区间直觉模糊决策的解决方案；文献[9]研究了云制造环境下，在考虑候选企业时序表现的基础上，基于广义优序法选择最优的合作伙伴。文献[10]在考虑企业主体心理的基础上，构建了云制造环境下合作伙伴的双向选择模型，并采用遗传算法进行求解。文献[11]通过能力、动机和可持续性三维度指标评价企业的可信度，采用实时编码遗传算法和非线性Hebbian学习算法，构建了基于信任的伙伴企业选择模型。

分析可见，这些研究在构建选择模型和优化算法时，比较注重候选企业的能力、资源、财务、可信度等定量和定性指标评价，而没有与驱动企业选择合作伙伴的需求联系起来，选出的合作伙伴可能很具优势，但不一定满足企业要求。本文所提基于模糊信息公理与云模型的虚拟合作伙伴选择方法，按照质量功能展开方法(Quality Function Deployment, QFD)[12,13]的步骤分析企业的合作需求，并利用相对偏好分析法计算属性相对权重；在引入模糊信息公理计算各候选企业的信息量后，利用逆向云发生器将各候选企业的评价结果转换成定性概念，在定量结果难以处理的情况下，通过分析评价结果的可靠性和稳定性推荐最恰当的合作企业。最后通过实例验证了所提方法的科学性和有效性。

1 理论基础

1.1 模糊信息公理

信息公理是Suh教授提出对设计方案进行评价的方法，目前已被广泛地应用到设计方案评价、先进制造系统选择、控制决策等领域。其基本思想是信息量最小的方案是最优方案，而信息量(I)是由满足需求的概率决定，即：

I=-log2P

(1)

其中：P是满足需要的成功概率，它是由评价指标期望的设计范围与系统实际范围确定，系统范围与设计范围的交集部分称为公共范围，信息量(I)也可表示为：

(2)

在合作伙伴评价选择过程中，需求属性可描述成定量数值，也可描述成不确定评价短语。针对不同的描述可采用不同的信息量计算方法。当第i个需求属性是一个实数xi时，其最优值为x01，最差值为x02，如果满足需求的概率P=xi/x01，对于成本型属性信息量计算公式为：

(3)

对于效益型属性信息量计算公式为：

(4)

对于不确定语义指标一般用模糊性语言来描述，如“非常差”、“差”、“较差”、“一般”、“较好”、“好”、“非常好”。如果以隶属函数的形式表示，如图1所示，可把每种语言形式化地表示成设计范围或系统范围。

图1 三角形隶属函数范围图

把系统范围曲线所围成的面积称为模糊系统范围(RFS)，设计范围隶属函数曲线围成的面积称为模糊设计范围(RFD)，交集所围成的面积称为模糊公共范围(RFC)，如图2所示：

图2 模糊范围示意图

则不确定语义模糊信息量计算为：

I=log2(RFS/RFC)

(5)

对于模糊设计范围是一区间，模糊系统范围是其中一部分的情况，式(5)已不适用，如模糊设计范围为评价短语“一般”至“非常好”，模糊系统范围为“一般”，则信息量计算改为：

I=log2(RFD/RFC)

(6)

如果用wj表示各决策属性权重，则评价方案综合信息量(IS)为：

(7)

式中wj由模糊QFD相关计算获得。

1.2 云模型

云模型[14～16]是由我国工程院院士李德毅提出的用以处理定量描述和定性概念不确定相互转换的模型，反映了概念或知识的随机性和模糊性，在研究了两者之间的关联性基础上，建立了定性和定量之间的映射关系。云模型能够把精确的数值转换为合适的定性语言描述，也能够从定性语言描述中得到定量数值的分布规律和取值范围。目前，云模型已被成功地应用到图像处理、数据挖掘、自然语言处理、智能控制、决策分析等众多领域[17]。

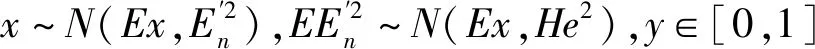
(8)

则yT(X):∀x∈U→[0,1]，即从论域U到区间[0,1]的映射被定义为云，记为云T(x)，每一个(x,y)称为一个云滴[13]。C(Ex,En,He)被称为云的特征向量，描述了云模型的整体特性，其中：Ex称为期望，是不确定性语义在论域上的中心位置，最能代表语义的值；En称为熵，表示不确定性语义随机性的度量，反映了定性概念云滴的离散程度；He称为超熵，表示熵的不确定程度，是熵模糊性与随机性的表现。

云模型利用云发生器实现定量和定性之间的互相转换，正向云发生器把定性概念数据转化为定量值和其确定度，其输入是定性概念的数字特征C(Ex,En,He)和云滴数n，输出是n个云滴数在数域空间上的位置和云滴代表定性概念的确定度y。逆向云发生器实现定量数据到定性概念的映射，其输入是符合一定规律的云滴样本，输出是由三个数字特征C(Ex,En,He)表示的定性概念。

2 基于模糊信息公理与云模型的合作伙伴选择

2.1 研究框架

合作伙伴选择过程是把企业的合作需求转换为合作企业选择决策属性，并在候选企业中选择最为合适合作伙伴的过程。对于同一合作需求，核心企业希望合作企业所具有的素质和提供服务是固定的，而各候选企业又具有各自的特性，本文以企业合作需求满意度最大化为优化目标，选取最优合作伙伴。本文所提基于模糊信息公理与云模型的合作伙伴选择过程如图3所示。具体选择步骤如下：

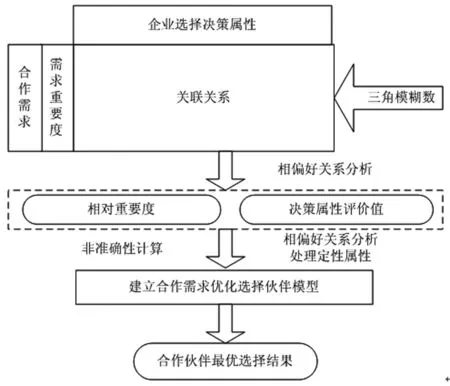
图3 需求驱动合作伙伴选择过程

步骤1组建专家组对企业合作需求进行分析，采用语义评价术语对合作需求重要度、合作需求与候选企业属性及提供服务间的关系进行评价，然后把这些不确定短语转换成模糊三角数，利用模糊三角数计算需求的重要度及合作需求与决策属性之间的模糊关联矩阵，并利用模糊偏好分析法得到各决策属性的相对权重值。

步骤2专家组调研、访谈候选企业，收集候选企业信息并评价。根据隶属函数特征确定各属性模糊设计范围和模糊系统范围，计算各候选企业信息量。

步骤3构建评价云的逆向发生器，生成各候选企业的定性评价云，以此为依据推荐出最恰当的合作伙伴。

2.2 基于模糊三角数的QFD相关计算

通过对核心企业的调研和访谈，可以得到核心企业合作需求为Ci(i=1,2,…,m)，合作伙伴选择决策属性为Mj(j=1,2,…,n)。专家采用语义评价企业合作需求及需求重要度和选择决策属性间的关系，并利用模糊三角数处理语义评价信息。

(9)

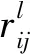
(10)

由此得到合作需求与决策属性间的关联关系矩阵R：

(11)

根据QFD计算要求，可得决策属性的重要度为：

(12)

2.3 基于相对偏好关系的相对重要度计算

(13)

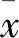
2.4 基于云模型合作伙伴优选

经过调研与访谈，专家组对各候选企业进行评价，根据数据类型的不同，由式(3)～式(7)计算各评价指标的信息量。以各信息量的值作为云滴的定量值，还原出各候选企业评价的云数字特征，根据这些数字特征选择出最为适合的合作伙伴。在定量评价的基础上，把定量结果转化成定性概念，可以充分表达出评价过程中存在的随机性和模糊性，使得评价结果更为严谨和客观。本文采用文献[18]所示的算法生成逆向云，可以由评价信息量得到定性概念的云数字特征。具体步骤如下：

输入：n个信息量Ij(j=1,2,…,n)。

输出：由数字特征C(Ex,En,He)表示的定性概念。

步骤1由n个信息量Ij(j=1,2,…,n)计算评价结果的均值：

(14)

步骤2计算En：

(15)

步骤3计算He:

(16)

把模糊信息公理与云模型结合起来评价候选企业，期望(Ex)越小表示其评价结果越好，熵(En)越小表示存在的不确定性也小；超熵(He)越小离散程度越小，表示其稳定性越好。

3 实例分析

国际某知名自动化设备企业发现品牌价值后，集中全部优势与资源发展品牌的影响力，以辐射生产与销售环节。发现中国市场不缺乏制造商，而且有着丰富的代工经验，也存在着现成的销售渠道。因此该企业决定借助先进的信息化技术，利用国内制造商的厂房、人工、技术和资金以及加盟商的销售渠道来弥补自身在中国的生产与销售不足，扩大品牌在中国的影响。由于品牌的价值决定了该企业的盟主地位，而其他企业是合作成员，由盟主企业管理和监督整个虚拟企业的生产、销售等经营行为。为了客观地选择合作伙伴，聘请业内专业人士组成20人专家组分析需求、调研候选企业，下面以制造企业的选择为例分析其选择过程。

经过对企业的调研与访谈可知盟主企业的对制造合作伙伴需求包括：良好的声誉(C1)、服务能力(C2)、合作动机(C3)、合作可持续性(C4)、低能耗(C5)。从员工、财务、技术、管理等方面对候选企业进行评价，结合需求选取评价指标包括：财务状况(M1)、人力资源状况(M2)、组织管理(M3)、技术水平(M4)、生产能力(M5)、节能方案(M6)、售后效率(M7)、历史经验(M8)、成本控制(M9)、合作需求(M10)、合作风险(M11)、和发展前景(M12)。研究表明人类普通区分级别为九级，根据实际情况与评价需要本文把评语分为七级，由表1把不确定评价短语转换成模糊三角数。

表1 不确定评价短语与模糊三角数的转换关系

专家组对合作需求重要度采用七等级不确定短语进行评价，根据表1把评价短语转换成模糊三角数，再由式(13)把模糊的合作需求转换成精确的需求权重，结果如表2所示。

表2 合作需求重要度评价与相对重要度

同样，由专家组采用评价短语对合作需求重要度与候选企业决策属性间的相互关系进行评价，再根据表1把评价短语转变成模糊三角数表示的模糊关联关系，如表3所示：

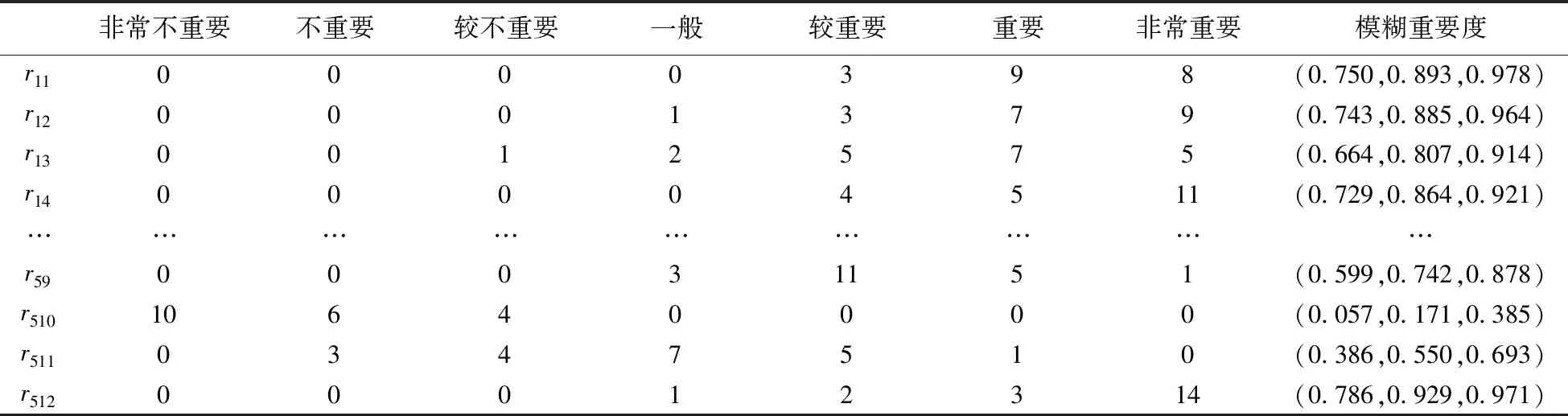
表3 合作需求与选择决策属性关联关系语义评价

然后，把合作需求与选择决策属性间的关联模糊三角数依次记录下来，由此得到合作需求与决策属性间的模糊关联矩阵，如表4所示：

表4 合作需求与选择决策属性模糊关联矩阵

根据表2与表4所提供数据，先由式(12)计算决策属性的相对重要程度，再由式(13)可得到各选择决策属性的相对重要度分别为：0.675，0.632，0.594，0.547，0.524，0.417，0.536，0.529，0.666，0.510，0.639，0.605。

随后，专家组对通过初选的五家候选企业进行调研与评价。M5、M7、M9为定量指标用数值表示，M5单位为台/月，成本控制由候选企业财务人员计算得到，售后效率统计近两年售后数据；定性指标由专家进行语义评价，如专家E1对五个候选企业评价如表5所示：

表5 专家E1对候选企业评价数据

表6 各候选企业属性信息量(专家E1)

对相对重要度归一化，并由式(7)可得专家E1对各候选企业评价的综合信息量为：0.774，0.755，0.619，0.767，0.620。同理，可得其他专家对各候选企业的综合评价信息量，进一步可算出各候选企业综合信息量均值。为了验证本方法的有效性，在此与文献[8]中的扩展TOPSIS方法和文献[9]中广义优序法进行对比，各方法计算结果如表7所示。

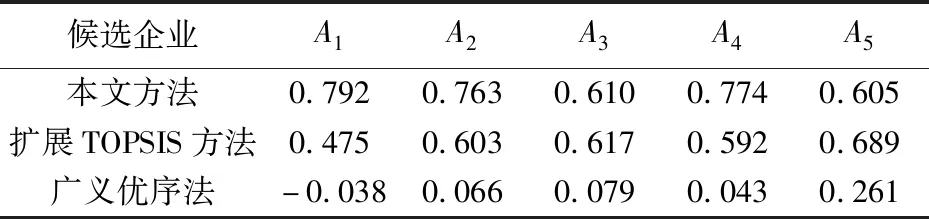
表7 各候选企业信息量均值

由表7可见，各方法的选择排序都为：A5>A3>A2>A4>A1，最优企业为A5，由此可得企业A5为最优合作企业，这也证明了本方法的有效性。在扩展TOPSIS方法中采用直觉模糊数处理语义模糊信息，随着评价指标的增多计算量会迅速上涨；在广义优序法中需要把数值或评价等级转化成优序数，其过程中可能会丢失部分信息；而模糊信息公理很好的处理信息的不确定性和模糊性，且计算简单，这一种很好的优选方法。

在实际应用中，不太满意的候选企业在初选时已被淘汰，聘请专家进行评价的企业，大部分是企业自身难以抉择的候选合作伙伴，因此，会出现评价结果相近的情况，如：企业A3与A5的评价结果十分的接近，企业A1、A2和A4的评价结果也基本在一个档次上。在出现多个评价结果相近时，由于综合信息量没考虑其它因素的差异，不能作进一步的分析，因此精确度较低，也没有定性分析，不符合人类决策的习惯。下面基于云模型对评价结果进行定性分析。首先以候选企业信息量作为云滴，运用式(14)～(16)计算各候选企业的云数字特征，计算结果如表8所示：

表8 各候选企业信息量云特征

与前面相同采用七级定性评语集，其对应的数字区间为(1.6,2)、(1.4,1.6]、(1.2,1.4]、(1.0,1.2]、(0.8,1.0]、(0.5,0.8]、[0,0.5]。可见企业A3与A5为好，A1、A2和A4为较好。企业A3与A5等级都为“好”，且Ex很接近，进一步借助云模型分析候选企业A3与A5，以企业A3与A5评价云模型数字特征为参数，可由正向云生成器生成企业A3与A5的云图进一步比较。在此我们把三种方法的评价结果生成关于企业A3与A5的云图，如图4、图5和图6所示：

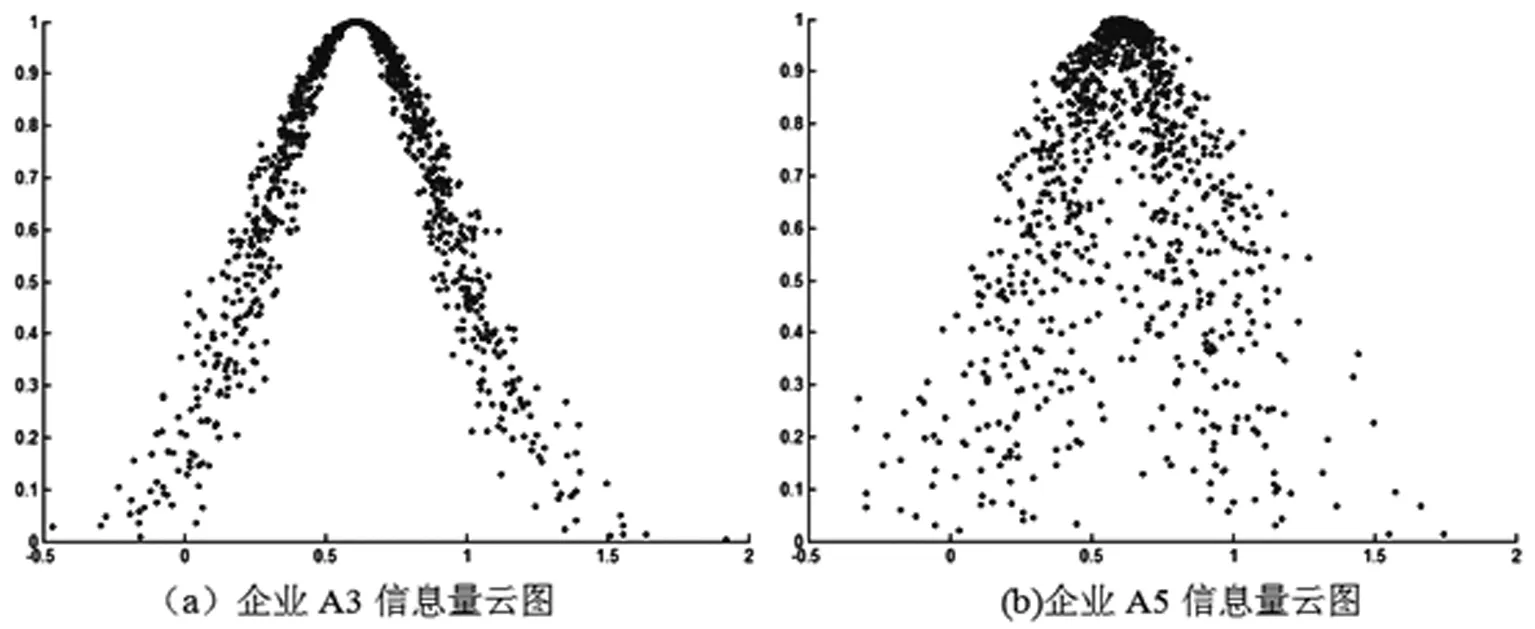
图4 本文方法云图

图5 扩展TOPSIS法云图

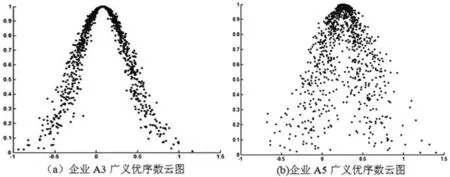
图6 广义优序法云图

在期望值很接近的情况下，熵和超熵也影响着评价的结果，它们反映了评价过程中的不确定性和随机性，反映了期望值的可信程度。从图4～图6来看，各方法生成的云图很接近，可见各专家组对企业A3的评价结果的云滴离散程度低、波动小，说明各位专家对企业A3的认识稳定，评价质量也是相对可靠；而对企业A5的评价结果云滴分散、跨度大，说明各位专家间对企业A5的认识存在差异，说明其期望值的可信度较企业A3低。由此可见在同一等级水平下，企业A3明显优于企业A5，因此最终推荐企业A3为合作企业，而不是仅靠综合信息量推荐的企业A5。但也可看出，图6的分散程度明显大于前两种方法，这也验证了在转换到广义优序数过程中存在着信息的丢失，增加了评价结果的分散性与不稳定性；由于生成的云图也存在随机性，另两种没有看出明显的判别。