考虑攻击相关性的蠕虫传播模型
2020-10-23宋明秋李艳博
宋明秋,李艳博
(大连理工大学 经济管理学院,辽宁 大连 116024)
0 引言
蠕虫一直是计算机网络安全的最大威胁之一。2017年5月,“永恒之蓝wanna cry”勒索蠕虫病毒肆虐全球,多国的政府机构和要害部门都遭到严重破坏。之后又接连发生了Petya、Locky、Bad Rabbit等蠕虫攻击事件,给社会经济带来了巨大的损失。蠕虫攻击之所以会产生如此大的影响,最根本的原因是蠕虫具有自我复制和传播的特性[1]。它可以借助被攻击节点发起对其他节点的新攻击,从而造成大规模网络瘫痪[2,3]。
对蠕虫在网络中传播行为的研究一直是学术界关注的焦点。目前蠕虫传播研究大多是基于传染病模型,包括SI、SIS、SIR、SEIR模型等[4~8]。经典的传染病模型是利用微分方程法描述一个完全连通网络上的传播行为。随着研究的不断深入,复杂网络理论指出Internet网络符合无标度网络特性,节点间的连接状况极不均匀,节点度服从幂律分布[9]。基于此,研究人员对传统微分方程法进行了改进,按照节点度对网络中的节点进行划分并分别建立微分方程[10,11]。改进后的方法虽然对度不同节点进行了区分,但是未考虑度相同节点间的差异性[12]以及传播过程中的概率事件[13],会导致不同程度的精确度问题。顾海俊等[14]利用状态转移概率法研究了病毒传播模型,发现概率方程法所求得的传播阈值更加接近仿真结果。状态转移概率法建立了离散时间下节点状态变化的概率,考虑了节点间的差异性问题,较微分方程法更具优势[15~17]。此方法对本文传播过程的描述具有一定的借鉴意义。
蠕虫在网络中的传播速度和传播规模与节点的感染概率相关。感染概率越大,蠕虫越容易扩散到整个网络。宋玉蓉等[18]认为节点度分布的不均匀性使节点拥有不同的安防强度,因此定义了与节点度相关的脆弱性函数来表征节点被感染的概率。李翔等[19]假定病毒的感染概率与个体脆弱程度和感染强度的乘积成正比例关系,研究了个体脆弱程度和感染强度服从幂率分布和高斯分布下的病毒传播临界行为。叶云等[20]考虑了CVSS标准中“Access Complexity”字段的属性值,并用其来表征攻击者渗透节点的难易程度。以上文献都对节点感染概率的研究做出了重大贡献,但是忽略了蠕虫攻击的相关性。罗宁等[21]指出入侵行为不再是单一行动,而表现为彼此协作入侵。经小川等[22]研究发现多个攻击行为同时发生时存在信息传递作用。文献[21,22]表明攻击具有相关性。当节点面临多个攻击行为时,这些攻击行为间的相互作用可能会对节点的脆弱性产生影响,从而促使蠕虫更容易完成对该节点的渗透过程,节点的感染概率增加。
根据上面的分析,本文研究了考虑攻击相关性的蠕虫传播模型,主要贡献为:在攻击具有相关性条件下对感染概率进行定量刻画;利用状态转移概率法对蠕虫传播过程进行数学建模,并推导对应的传播临界值表达式;在无标度网络中对蠕虫传播模型进行仿真实验,研究感染概率初始值、感染变化率以及传播概率对蠕虫传播过程和最终规模的影响,为蠕虫传播的控制提供借鉴和参考。
1 考虑攻击相关性的蠕虫传播模型
1.1 攻击相关性
蠕虫攻击是指蠕虫程序利用节点的脆弱性对其完成入侵渗透的过程。根据攻击渗透理论模型,攻击渗透的结果是节点脆弱性的增加以及用户权限的提升等[23]。由此发现,当节点同时受到多个邻居已感染节点发起的攻击时,一部分邻居节点入侵渗透带来的节点脆弱性增加以及用户权限的提升等结果可能会成为该节点被其他邻居节点攻击的前提,从而使后一部分邻居节点的入侵渗透更容易完成;同时根据协作入侵理论,多攻击行为可以构成一个攻击序列,它们之间存在的信息传递作用会不断地对节点的脆弱性产生影响[22]。根据上述理论分析可以发现,多攻击行为在入侵渗透过程中具有相关性,并且攻击相关性会导致节点的脆弱性增加,节点的感染概率增大。为了更加准确地描述多攻击行为下节点感染概率的动态性,在蠕虫传播模型的构建中应将攻击相关性纳入考虑范围。
1.2 考虑攻击相关性的蠕虫传播模型假设
对蠕虫在网络中的传播做如下假设:
(1)网络中节点的所有连边都具有均匀的传输能力,即节点的传播概率是一个常量;
(2)节点不论度大小都具有相同的安防强度,即节点的初始感染概率相同;
(3)节点被成功感染的概率和该节点的邻居感染状态节点数目相关。
假设(1)和(2)是无标度网络传播模型研究中的两个重要基本假设[10]。本文模型在这两个基本假设的基础上考虑了攻击相关性:网络中节点度越大,该节点可能受到的攻击越多,这些攻击间的相关性会导致节点的脆弱性增加,被感染的概率增大。
1.3 考虑攻击相关性的STIR蠕虫传播模型构建
将计算机网络抽象为一个无向网络,记作G=(V,E)。V表示网络中的节点,E表示节点间的连边。该网络的邻接矩阵为A=[wij]N×N。当节点i和节点j之间存在通信连接时,wij=1;否则,wij=0。
1.3.1 节点描述
蠕虫攻击包括传播和感染两个过程。传播是指蠕虫借助宿主节点向邻居节点发起攻击的过程。感染是指蠕虫程序利用被攻击节点的漏洞对其入侵渗透的过程。在传染病基本模型SIR中,节点由S状态到I状态的转变是一步完成的,没有根据蠕虫攻击的两个过程对节点状态进行细分。为了从微观层面更贴合实际传播过程,本文在SIR模型的基础上引入威胁状态T,将S→I的状态转变更新为S→T→I,分别对应蠕虫攻击的传播和感染两阶段过程,相应的传播模型称为STIR模型。
节点状态的具体描述如下:
定义1节点状态
易感状态S(Susceptible):该类节点存在漏洞,可能会受到蠕虫的攻击;
威胁状态T(Threatened):该类节点已经受到蠕虫的攻击扫描,还未被入侵渗透,不具备传播能力;
感染状态I(Infectious):该类节点已经被蠕虫成功侵入,具备传播能力;
免疫状态R(Recovered):该类节点通过安装杀毒软件、系统升级等操作获得了免疫能力,不会被蠕虫感染,也不具备传播能力。
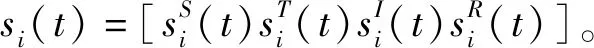
1.3.2 蠕虫传播规则
蠕虫在STIR模型中的传播过程如图1所示,具体传播规则如下:
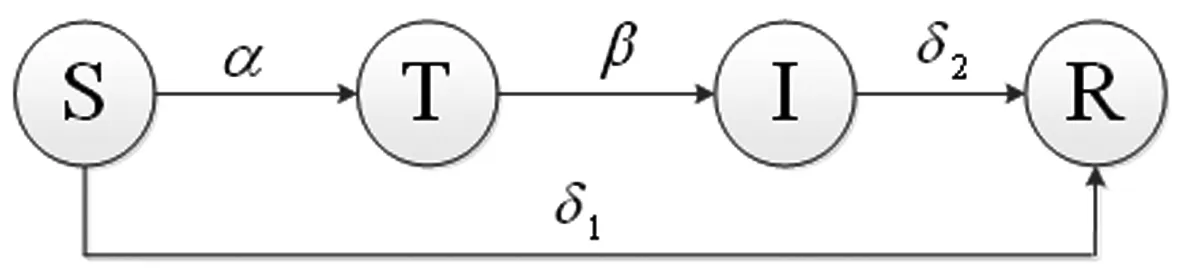
图1 STIR模型的状态转换图
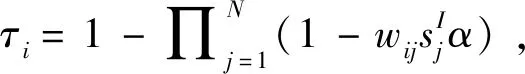
(2)威胁状态节点i将以概率βi被成功入侵渗透而成为感染状态,其中βi表示节点i的感染概率;
(3)处于易感状态和感染状态的节点分别以概率δ1和δ2转变为免疫状态,其中δ1和δ2表示节点的免疫概率。
1.3.3 感染概率
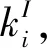
(1)
其中,β0和Δβ为感染概率参数,体现了感染概率曲线的特征。β0表示感染概率初始值,体现了初始状态下网络节点的脆弱性,其值越大,节点的脆弱性越大,被感染的概率越大。Δβ为感染变化率,表示感染概率对攻击数目变化的敏感程度,其值越大,感染概率对攻击数目的变化越敏感,节点被感染的概率越大。若感染概率β(t)>1,取β(t)=1。
2 基于状态转移的蠕虫传播动力学方程
根据上面描述的蠕虫传播过程,利用状态转移概率法可建立如下的蠕虫传播动力学方程:
(2)
(3)
Si(t+1)=MulitiRealize[Pi(t+1)]
(4)
其中,MultiRealize[Pi(t+1)]是根据给定Pi(t+1)的概率分布随机实现的节点i在t时刻的状态。
参照文献[14]中的方法,将上述方程转化为下式:
(5)
此时节点i受到攻击的概率为:
(6)
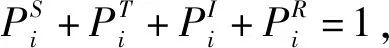
(7)
(8)
上式是一个非线性动力学系统F:[0,1]3N→[0,1]3N,系统初始节点(xi,yi,zi)=(0,0,0),∀i∈{1,…,N}为固定点,通过雅克比矩阵来分析方程在初始点的局部稳定性。
方程的雅可比矩阵为:
(9)
矩阵(9)的特征根为:
(10)
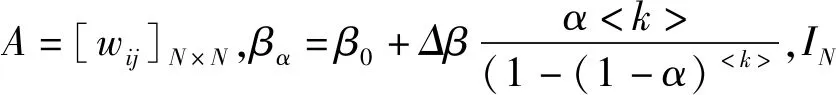
当满足max{d1,d2,d3}<1时,初始节点局部稳定。因0<δ1<1,故d1<1,d3<1恒成立。
由d2<1可以得到:
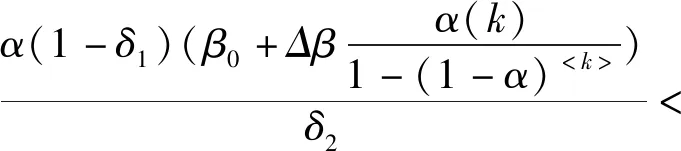

(11)
因此,本文模型的有效传播率
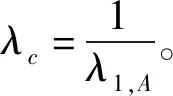
3 仿真分析
本文将建立的考虑攻击相关性的蠕虫传播模型在无标度网络中进行仿真实验。实验目的是讨论考虑攻击相关性的感染概率对蠕虫传播过程的影响,具体分析了感染概率初始值、感染变化率以及传播概率三个参数的作用。
仿真实验是依托Matlab实验平台,构建的无标度网络中节点总数N=1000,节点平均度
3.1 蠕虫传播临界值分析
上文通过数学推导得出了有效传播率λ*和传播临界值λc的计算公式,现利用仿真实验来研究它们之间的关系。设定免疫概率δ1=0、δ2=1,感染变化率Δβ=0.1,通过改变传播概率α、感染概率初始值β0来调节有效传播率。实验参数设置见表1,仿真实验结果如图2所示。
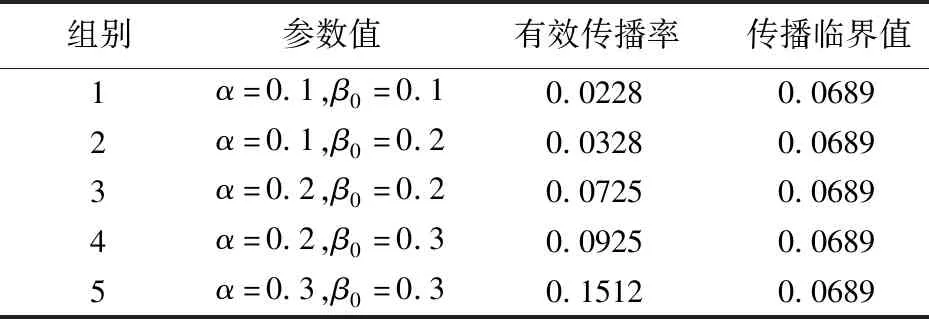
表1 有效传播率和传播临界值的对比
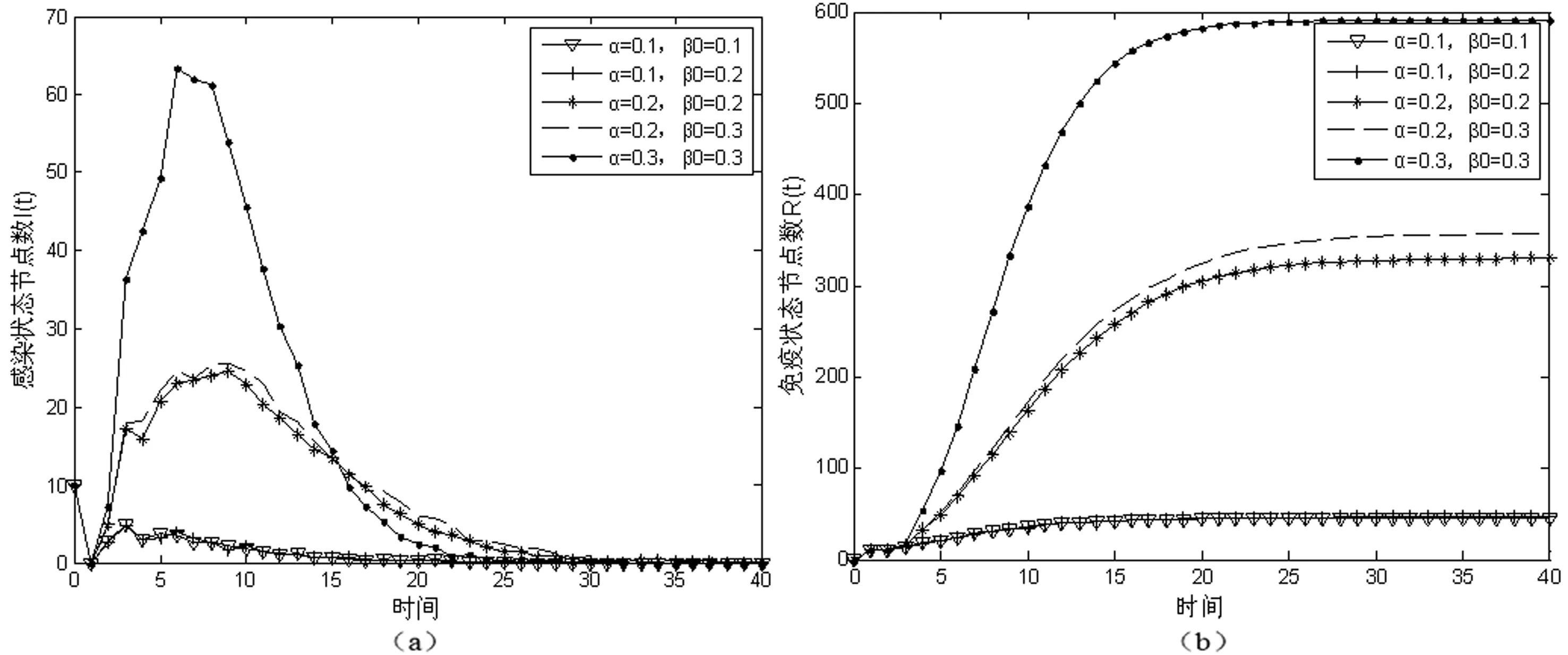
图2 参数值对传播过程的影响
图2(a)和(b)分别代表感染状态节点数目I(t)和免疫状态节点数目R(t)随时间的变化情况。由表1可知,前两组实验的有效传播率均小于传播临界值。图2中这两组的I(t)随时间不断减小,R(t)由0逐渐增加并最终稳定在初始感染状态节点数目附近;表1中后三组实验的有效传播率均大于传播临界值,表明蠕虫会在网络中大范围爆发。图2中后三组实验的I(t)出现了大幅度增加,到达峰值后又逐渐减少为0。R(t)随t逐渐增加,后稳定于某值。通过以上分析,发现图2的仿真结果和表1中的数值结果是一致的。因此,仿真实验验证了模型数值推导的正确性。
3.2 感染概率对蠕虫传播的影响分析
为研究考虑攻击相关性前后感染概率对蠕虫传播过程的影响,将本文模型的实验结果与文献[14]的实验结果进行比较分析。为保证两个实验的可比性,表2中对概率参数进行了相关设定。仿真实验结果如图3所示。

表2 模型参数设置
从图3可以发现,本文STIR模型在考虑攻击相关性情况下得出的蠕虫感染规模整体上要高于文献[14]的结果。在起初较短的时间内,两组各状态节点数目的变化情况几乎相同。这表明蠕虫传播初期,感染概率的大小对传播的影响很小。经过一定时间后,两组的差异性开始显现。相比于文献[14],本文模型中蠕虫传播速度更快、传播范围更广。这是因为在本文模型中节点的感染概率会随其受到攻击数目的增加而增大。感染概率的增大加快了感染状态节点数目I(t)的增长速度。同时,网络中I(t)的增多也会使节点受到蠕虫攻击的概率变大,威胁状态节点数目T(t)变多。以上仿真结果与实际情况相一致。在网络环境中,当单个节点受到多个攻击行为时,该节点被感染的可能性更大。因此,在计算节点的感染概率时应该考虑攻击相关性,否则将会低估蠕虫在网络中的传播能力。
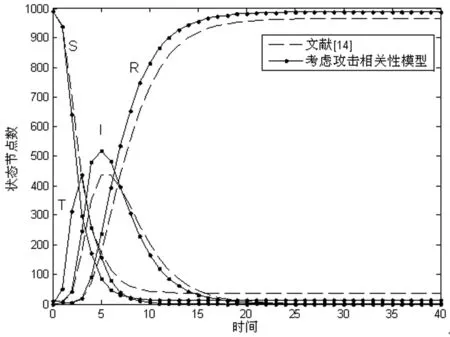
图3 感染概率对蠕虫传播的影响
从图3还可以看出,I(t)在到达峰值之后会呈现下降趋势。这是因为此时节点由I状态转变为R状态的数目大于由T状态转变为I状态的数目。I(t)的下降速度是先增大后减小。在I(t)下降的初始阶段,T(t)减小的速度比较快,这使得I(t)的下降速度加快;当T(t)下降到某一值时,T(t)对I(t)的影响会变得很小,此时I(t)的下降主要取决于I状态转变为R状态的节点数目。免疫概率δ2=0.3固定不变,随着I(t)逐渐减小,I(t)的下降速度变缓。
3.3 感染概率初始值对蠕虫传播的影响分析
为研究感染概率初始值β0在不同取值情况下对蠕虫传播过程的影响,设计了三组对比实验。其中,β0分别为0.4、0.6、0.8。传播概率α=0.8,感染变化率Δβ=0.05,仿真实验结果如图4所示。
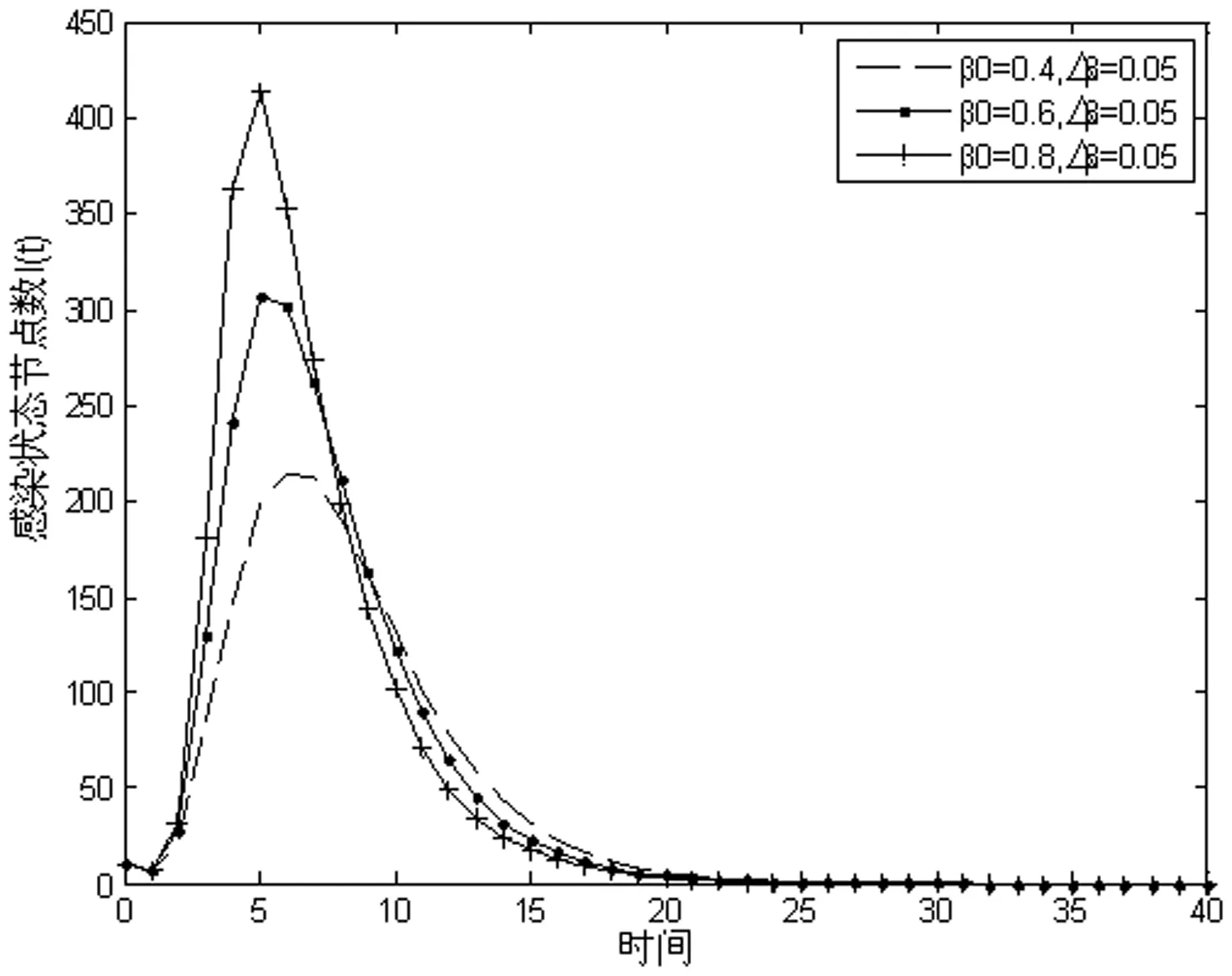
图4 感染概率初始值对蠕虫传播的影响
从图4可以看出,感染概率初始值β0越大,感染状态节点数目I(t)在达到峰值前的增长速度越快,峰值越高。参数β0代表节点的初始脆弱性,它的值越大,表明初始状态时节点的自身抵抗力越弱,漏洞匹配越高,因此节点被感染的概率越大,网络中蠕虫的传播速度越快、传播范围越广。根据上面的分析,在计算机网络中可以通过提升节点主机的安全性来降低蠕虫的传播规模。因此,需要定期对主机进行漏洞修补和病毒查杀,提高其抵抗攻击的能力。
3.4 感染变化率对蠕虫传播的影响分析
为研究感染变化率对蠕虫传播过程的影响,将感染变化率β0设定为三个水平:0.01、0.05、0.1。实验中传播概率α=0.8,感染概率初始值β0=0.6。仿真结果如图5所示。
由图5可知,随着Δβ的增加,网络中感染状态节点数目I(t)的增长速度变快,峰值变高。感染变化率Δβ的含义是节点的感染概率对蠕虫攻击数目变化的敏感性。当节点面临多个攻击行为时,感染变化率越大,表明该节点的感染概率对攻击数目变化越敏感,因此节点被感染的可能性越大,网络中感染节点的规模也就越大。根据实验结果,网络节点在得知存在蠕虫病毒传播后,需要及时断开与感染状态节点的连接,防范多威胁主体的联合攻击。
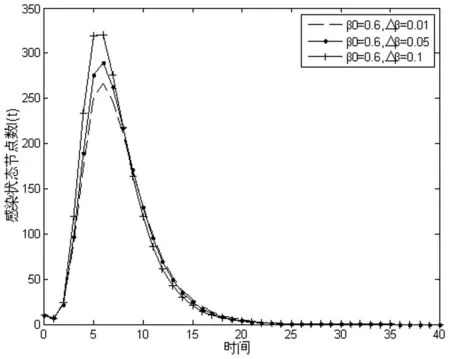
图5 感染变化率对蠕虫传播的影响
3.5 传播概率对蠕虫传播的影响分析
设定感染概率初始值β0=0.6,感染变化率Δβ=0.05,研究传播概率α对蠕虫传播过程的影响。其中,α分别取0.4、0.6、0.8,实验结果见图6。
从图6可以看出,传播概率α越大,网络中威胁状态节点数目T(t)的增长速度越快,峰值越高。感染状态节点数目I(t)的变化规律和T(t)一致。传播概率α可以理解为节点成功受到邻居感染状态节点攻击的概率,其值越大,表明该节点受到攻击威胁的可能性越大,从而导致节点被感染的概率增加。根据上述分析,网络中的计算机需要加强对访问控制和自我防护的管理。主机在交互前需要进行必要的入侵检测。假若遭遇异常交互,应该及时采取措施进行阻拦。
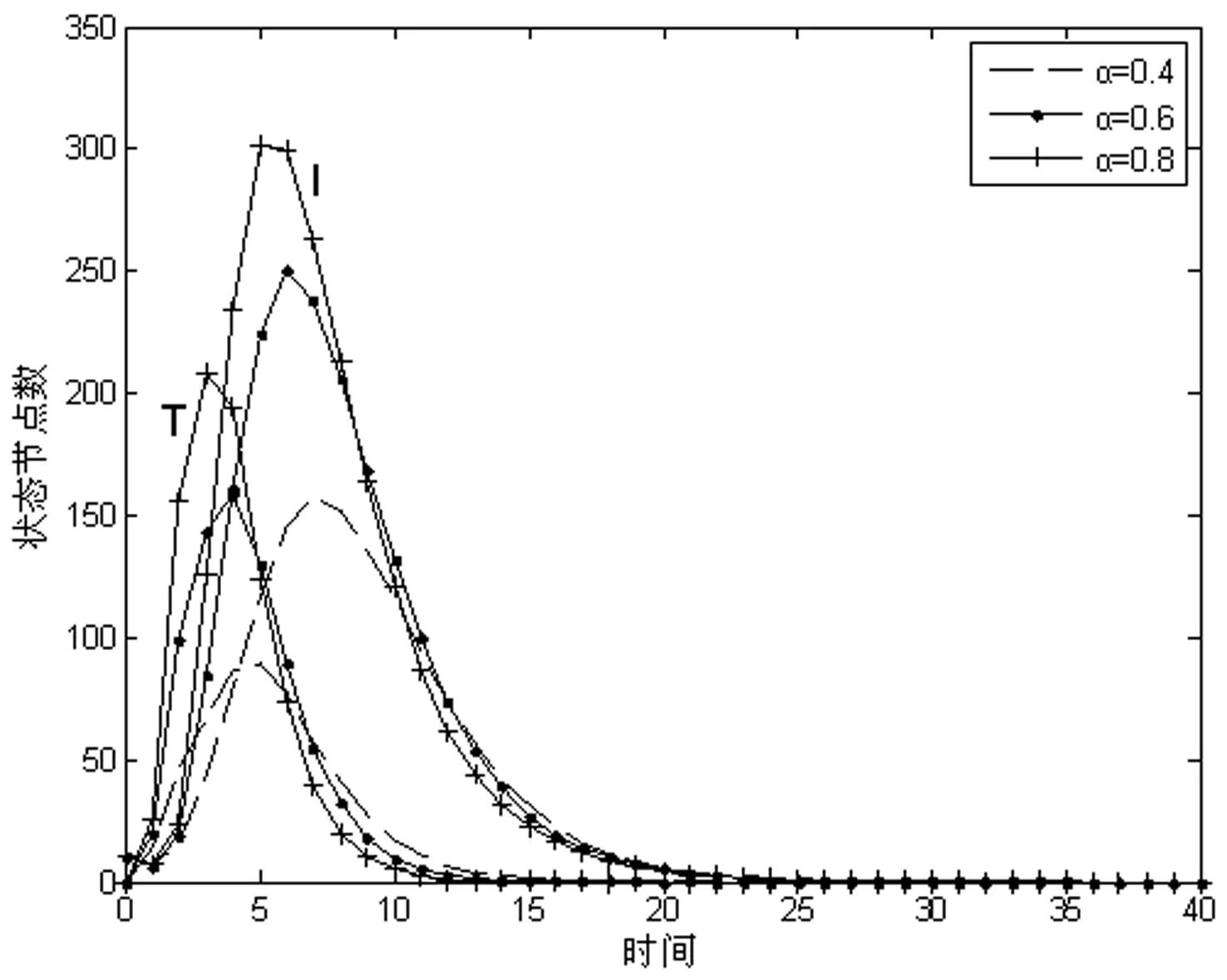
图6 传播概率对蠕虫传播的影响
4 结论
本文提出了一种考虑攻击相关性的蠕虫传播模型-STIR。根据邻居节点中处于感染状态的节点数目,动态调整被攻击节点的感染概率,并利用状态转移概率法描述蠕虫的传播过程,最后在无标度网络中进行了仿真实验。
结果表明:STIR蠕虫传播模型提高了感染概率计算的准确性,能够更好地描述蠕虫的传播能力;模型中重要参数——蠕虫的有效传播率λ*由传播概率α、感染概率初始值β0、感染变化率Δβ、免疫概率δ1、δ2以及网络中节点的平均度
